Rapid Profile Variations in the Broad Hα Line of the Seyfert Galaxy Markarian 6: Possible Evidence for Turbulence in the Accretion Disk

Extract

We report on implications for the geometrical and kinematic parameters of BLR gas on the basis of short timescale variability in the broad Hα profile shape. Data on rapid variations have been obtained at the 2.6−m telescope of the BAO (Asatrian, Khachikian & Notni, 1999). To search for variations in the profile, difference spectra (second minus first epoch) were examined. We believe that the structure of the underlying stellar continuum and the atmospheric features do not affect significantly the Hα difference profiles of Mark 6. Variations occurred simultaneously on the blue and red sides of Hα on a time scale of ≃ 50.7 minutes and take the form of three narrow, positive small bumps on each side in the difference spectrum. The positions of the bumps are −4400, −3100, −1700 and +1900, +4200 and +6600 kms⁻¹. These changes may indicate the response of circularly rotating emitting gas at three orbits to a light pulse from a central source. In this case the pairs of blue and red bumps observed at −4400 and +6600, −3100 and +4200, and −1700 and 1900 km s⁻¹ are formed in two opposite zones of gas close to the line of nodes. On the assumption that these orbits lie around a central massive object, orbital parameters (radii, velocities and inclination angles of orbital planes) of the clouds and the central mass can be found. The shift of each bump is defined by the combination of the relativistic Doppler effect due to the Keplerian orbital motion and the gravitational redshift. The six observed radial velocities are determined by six parameters: the orbital radii, R₁, R₂, R₃ (or velocities, V_i, V₂, V₃) and the inclination angles i₁, i₂, i₃ of the rotation planes. Thus, the expressions for the radial velocities form a system of six algebraic equations with six unknowns and can be solved. Using the difference of the orbital radii in absolute units (R₃ − R₁ = Δt C, where ΔtC, ≃ 50.7 minutes and C is the speed of light) we can derive the central mass M. Analytical solution gives: 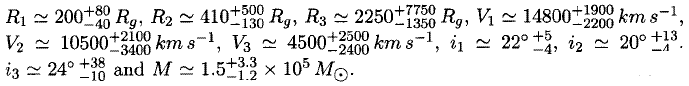Error limits for the results are determined by the uncertainty of the input radial velocities, 300 km s⁻¹. However, the value of the mass obtained is smaller by two orders of magnitude than the estimate for the dynamical mass of the nucleus of Mark 6 (M = 1 × 10⁷M_⊙ Dibai 1984). Such a low mass is excluded, therefore.