Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T03:07:46.570Z Has data issue: false hasContentIssue false
  • English
  • Français

The Oscillation of a System Earth – Moon

Published online by Cambridge University Press:  12 April 2016

G. Kurbasova  and
L. Rykhlova
G. Kurbasova
Affiliation:
Crimea Astrophysical Observatory, Ukrainian Academy of Sciences, p/o Nauchnyi, Crimea, 334413Ukraine, e-mail:[email protected]
L. Rykhlova
Affiliation:
Institute for Astronomy, Russian Academy of Sciences, 109017 Pyatnitskaya Str. 48, Moscow, Russia. e-mail:[email protected]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Internal links in the Earth-Moon system are determined by gravitational interaction. According to the least compulsion principle of Gauss, the deviation of “free motion” of heliocentric orbits of two material points with Earth and Moon masses is determined by the sum of the products of each material points’ deviation from its free motion and its mass.

By solving the minimization problem using the Lagrange multiplier method, Lagrange equations of the first kind were obtained in vector form. With acceptable assumptions (introduction of non-dimensional time τ = nt, where n is the sidereal rotation of the Moon, and the lunar orbit is considered to be circular) the linkage coefficient (Lagrange multiplier) is:

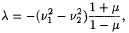
where v1and v2 are proper frequencies of the Earth and the Moon and μ is the Moon/Earth mass ratio.

Type
Part 5. Chandler and Annual Polar Motion: Observations and Excitation
Information
International Astronomical Union Colloquium , Volume 178: Polar Motion: Historical and Scientific Problems , 2000 , pp. 493 - 494
Copyright
Copyright © Astronomical Society of the Pacific 2000

References

Mandelshtam, L.I., 1972, Complete set of the transaction, Vol IV, Moscow: Nauka, 512 pp.Google Scholar