No CrossRef data available.
Published online by Cambridge University Press: 12 April 2016
Dynamical systems with three degrees of freedom can be reduced to the study of a four-dimensional mapping. We consider here, as a model problem, the mapping given by the following equations:
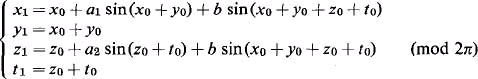
We have found that as soon as b ≠ 0, i.e. even for a very weak coupling, a dynamical system with three degrees of freedom has in general either two or zero isolating integrals (besides the usual energy integral).