Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2025-01-06T02:30:22.628Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical Simulation of the Rotational Motion of the Earth and Moon

Published online by Cambridge University Press:  12 April 2016

G.I. Eroshkin  and
V.V. Pashkevich
G.I. Eroshkin
Affiliation:
Institute of Theoretical Astronomy, Russian Acad, of Sciences St. Petersburg, Russia
V.V. Pashkevich
Affiliation:
Institute of Theoretical Astronomy, Russian Acad, of Sciences St. Petersburg, Russia

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dynamics of the rotational motion of the Earth and Moon is investigated numerically. Very convenient Rodrigues-Hamilton parameters are used for high-precision numerical integration of the rotational motion equations in the post-newtonian approximation over a 400 yr time interval. The results of the numerical solution of the problem are compared with the contemporary analytical theories of the Earth’s and Moon’s rotation. The analytical theory of the Earth’s rotation is composed of the precession theory (Lieske et al., 1977), nutation theory (Souchay and Kinoshita, 1996) and geodesic nutation solution (Fukushima, 1991). The analytical theory of the Moon’s rotation consists of the so-called Cassini relations and the analytical solutions of the lunar physical libration problem (Moons, 1982), (Moons, 1984), (Pešek, 1982). The comparisons reveal residuals both of periodic and systematic character. All the secular and periodic terms representing the behavior of the residuals are interpreted as corrections to the mentioned analytical theories. In particular, the secular rate of the luni-solar inclination of the ecliptic to the equator J2000.0 (–0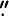027, with a mean square error 0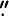000005) is very close to its theoretical value (Williams, 1994).

Type
Rotation of Solar System Objects
Information
International Astronomical Union Colloquium , Volume 165: Dynamics and Astrometry of Natural and Artificial Celestial Bodies , 1997 , pp. 275 - 280
Copyright
Copyright © Kluwer 1997

References

Belikov, M.V.: 1993, “Methods of numeiical integration with uniform and mean square approximation for solving problems of ephemeris astronomy and satellite geodesy”, Manuscr. Geod. 15, 182–200.Google Scholar
Eroshkin, G.I., Taibatorov, K.A., and Trubitsina, A.A.: 1993, “Constructing the specialized numerical ephemerides of the Moon and the Sun for solving the problems of the Earth’s artificial satellite dynamics”, ITA R.A.S., Preprint No 31 (in Russian).Google Scholar
Fukushima, T.: 1991, “Geodesic nutation”, Astron. Astrophys. 244, 1, L11–L12.Google Scholar
Lieske, J.H., Lederle, T., Fricke, W., and Morando, B.: 1977, “Expression for the precession quantities based upon the IAU (1976) system of astronomical constants”, Astron. Astrophys. 58, 1/2, 1–16.Google Scholar
Moons, M.: 1982, “Physical libration of the Moon”, Celest. Mech. 26, 131–142.CrossRefGoogle Scholar
Moons, M.: 1984, “Planetary perturbations on the libration of the Moon”, Celest. Mech. 34, 263–273.CrossRefGoogle Scholar
Pešek, L.: 1982, “An effect of the Earth’s flattening on the rotation of the Moon”, Bull. Astron. Inst. Czechosl. 33, 176–179.Google Scholar
Simon, J.L., Bretagnon, P., Chapront, J., Chapront-Touze, M., Francou, G., and Laskar, J.: 1993, “Numerical expressions for precession formulae and mean elements for the Moon and the planets”, Bureau des Longitudes, Preprint No 9302.Google Scholar
Souchay, J. and Kinoshita, H.: 1996, “SKRE96: The theory of the nutation of the rigid Earth”, private communication.Google Scholar
Williams, J.G.: 1994, “Contributions to the Earth’s obliquity rate, precession, and nutation”, Astron. J. 108, 711–724.CrossRefGoogle Scholar