Nekhoroshev-Stability of L₄ and L₅ in the Spatial Restricted Problem

Extract

The Lagrangian equilateral points L₄ and L₅ of the restricted circular three-body problem are elliptic for all values of the reduced mass μ below Routh’s critical mass μ_R ≈ .0385. In the spatial case, because of the possibility of Arnold diffusion, KAM theory does not provide Lyapunov-stability. Nevertheless, one can consider the so-called ‘Nekhoroshev-stability’: denoting by d a convenient distance from the equilibrium point, one asks whether

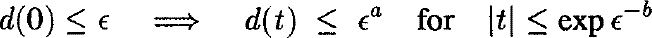
for any small єe > 0, with positive a and b. Until recently this problem, as more generally the problem of Nekhoroshev-stability of elliptic equilibria of Hamiltonian systems, was studied only under some arithmetic conditions on the frequencies, and thus on μ (see e.g .Giorgilli, 1989). Our aim was instead considering all values of μ up to μ_R. As a matter of fact, Nekhoroshev-stability of elliptic equilibria, without any arithmetic assumption on the frequencies, was proved recently under the hypothesis that the fourth order Birkhoff normal form of the Hamiltonian exists and satisfies a ‘quasi-convexity’ assumption (Fassò et al, 1998; Guzzo et al, 1998; Niedermann, 1998).