Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T08:41:47.649Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of The Quadrupole Moment of The Sun on The Dynamics of The Earth-Moon System

Published online by Cambridge University Press:  12 April 2016

E. Bois  and
J.F. Girard
E. Bois
Affiliation:
Observatoire de Bordeaux, UMR/CNRS/INSU 5804 B.P. 89, F-33270 Floirac, FranceE-mail:, [email protected]
J.F. Girard
Affiliation:
Observatoire de Bordeaux, UMR/CNRS/INSU 5804 B.P. 89, F-33270 Floirac, FranceE-mail:, [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Range of values of the Sun’s mass quadrupole moment of coefficient J2 arising both from experimental and theoretical determinations enlarge across literature on two orders of magnitude, from around 10−7 until to 10−5. The accurate knowledge of the Moon’s physical librations, for which the Lunar Laser Ranging data reach an outstanding precision level, prove to be appropriate to reduce the interval of J2 values by giving an upper bound of J2. A solar quadrupole moment as high as 1.1 10−5 given either from the upper bounds of the error bars of the observations, or from the Roche’s theory, is not compatible with the knowledge of the lunar librations accurately modeled and observed with the LLR experiment The suitable values of J2 have to be smaller than 3.0 10−6.

As a consequence, this upper bound of 3.0 10−6 is accepted to study the impact of the Sun’s quadrupole moment of mass on the dynamics of the Earth-Moon system. Such an effect (with J2 = 5.5 ± 1.3 × 10−6) has been already tested in 1983 by Campbell & Moffat using analytical approximate equations, and thus for the orbits of Mercury, Venus, the Earth and Icarus. The approximate equations are no longer sufficient compared with present observational data and exact equations are required. As if to compute the effect on the lunar librations, we have used our BJV relativistic model of solar system integration including the spin-orbit coupled motion of the Moon. The model is solved by numerical integration. The BJV model stems from general relativity by using the DSX formalism for purposes of celestial mechanics when it is about to deal with a system of n extended, weakly self-gravitating, rotating and deformable bodies in mutual interactions.

The resulting effects on the orbital elements of the Earth have been computed and plotted over 160 and 1600 years. The impact of the quadrupole moment of the Sun on the Earth’s orbital motion is mainly characterized by variations of 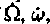, and Ė. As a consequence, the Sun’s quadrupole moment of mass could play a sensible role over long time periods of integration of solar system models.

Keywords

: SunQuadrupoleMoonLibrationEarthLLR data
Type
Planets and Satellites
Information
International Astronomical Union Colloquium , Volume 172: Impact of Modern Dynamics in Astronomy , 1999 , pp. 329 - 338
Copyright
Copyright © Kluwer 1999

References

Bois, E., Boudin, F., Journet, A.: 1996, ‘Secular Variation of the Moon’s Rotation Rate’, A&A 314, pp. 989–994.Google Scholar
Bois, E., Journet, A.: 1993, ‘Lunar and Terrestrial Tidal Effects on the Moon’s Rotational Motion’, Celest. Mech. 57, pp. 295–305.Google Scholar
Bois, E., Vokrouhlický, D.: 1995, ‘Relativistic Spin Effects in the Earth-Moon System’, A&A 300, pp. 559–567.Google Scholar
Bois, E., Wytrzyszczak, I., Journet, A.: 1992, ‘Planetary and Figure-figure Effects on the Moon’s Rotational Motion’, Celest. Mech. 53, pp. 185–201.CrossRefGoogle Scholar
Campbell, L., and Moffat, J.W.: 1983, ‘Quadrapole Moment of the Sun and the Planetary Orbits’, The Astrophys. Journal 275, L77–L79 Google Scholar
Damour, T., Soffel, M., Xu, Ch.: 1991, 1992, 1993, 1994, ‘General Relativistic Celestial Mechanics’, Phys. Rev. D43, 3273, D45, 1017, D47, 3124, D49, 618.Google Scholar
Dickey, J.O., Bender, P., Faller, J., et al.: 1994, ‘Lunar Laser Ranging: A Continuing Legacy of the Apollo Program’, Science 265, pp. 482–490.CrossRefGoogle ScholarPubMed
Moons, M.: 1984, ‘Planetary Perturbations on the Libration of the Moon’, Celest. Mech. 34, pp.263–273.CrossRefGoogle Scholar
Müller, J., Schneider, M., Soffel, M., Ruder, H.: 1996, ‘Determination of Relativistic Quantities by analyzing Lunar Laser Ranging Data’, in: Proceedings of the 7th Marcel Grossmann Meeting, eds. Jantzen, R. and Mac Keiser, G., 1517.Google Scholar
Pijpers, F.P.: 1998, ‘Helioseismic determination of the solar gravitational quadrapole moment’, Mon. Not. R. Astron. Soc. 297, pp. L76–L80 Google Scholar
Rozelot, J.-P., and Bois, E.: 1998, ‘New Results Concerning the Solar Oblateness’, Synoptic Solar Physics, ASP Conf. Series 140, pp. 75–82 Google Scholar
Williams, J.G., Newhall, X.X., and Dickey, J.O.: 1995, ‘Relativity Parameters Determined from Lunar Laser Ranging’, Phys. Rev. D53, pp. 6730–6739.Google Scholar