Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T03:15:21.703Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansion of the Disturbing Function by Factorization

Published online by Cambridge University Press:  12 April 2016

R. Broucke  and
W. Presler
R. Broucke
Affiliation:
Department of Aerospace Engineering and Engineering Mechanics University of Texas at Austin, Texas 78712
W. Presler
Affiliation:
Department of Aerospace Engineering and Engineering Mechanics University of Texas at Austin, Texas 78712

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present an expansion of the disturbing function for the third-body perturbations in the form 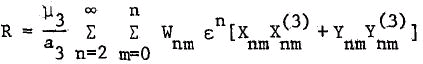, where ε is the ratio of semi-major axes (a/a’) and Xnm and Ynm depend only on the five elements e, i, ω, Ω, of the satellite while 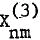and 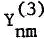depend on the corresponding elements of the perturbing body. Each one of the four functions X and Y is represented as a product of two factors as opposed to three factors in our previous publication of this subject (Broucke, 1981). We develop several relations for the construction of the X and Y-series. These series are relatively short and can be computed in advance and stored on magnetic tape, for instance.

Type
Part IV
Information
International Astronomical Union Colloquium , Volume 63: High-Precision Earth Rotation and Earth-Moon Dynamics , May 1981 , pp. 337 - 348
Copyright
Copyright © Reidel 1982

References

1. Broucke, R., and Smith, G., “Expansion of the Planetary Disturbing Function,” Celestial Mechanics, Vol. 3, pp. 408–426, 1971.Google Scholar
2. Broucke, R., “Expansion of the Third-Body Disturbing Function,” J. of Guidance and Control, Vol. 4, No. 3, pp. 346–348, 1981.Google Scholar
3. Cefola, P., and Broucke, R., “On the Formulation of the Gravitational Potential in Terms of the Equinoctial Variables,” AIAA Paper No. 75-9, AIAA 13th Aerospace Sciences Meeting, Pasadena, California, January 20-22, 1975.Google Scholar
4. Petrovskaya, M.S., “Expansions of the Negative Powers of Mutual Distances between Bodies,” Celestial Mechanics, Vol. 3, No. 1, pp. 121–128, 1970.Google Scholar
5. Yuasa, M., and Hori, G., “New Approach to the Planetary Theory,” in: Duncombe, R. L. (ed.), Dynamics of the Solar System, pp. 69–72, 1979.Google Scholar