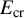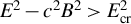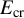1 Introduction
Progress in high-power laser technology in recent decades has made it possible, through the generation of extraordinarily strong electromagnetic (EM) fields, to investigate radiation and particle-production processes in the nonlinear quantum regime[ Reference Dittrich and Gies1– Reference Yoon, Kim, Choi, Sung, Lee, Lee and Nam10]. In addition, this has opened up new opportunities for the creation of exotic particle and radiation sources[ Reference Gonoskov, Bashinov, Gonoskov, Harvey, Ilderton, Kim, Marklund, Mourou and Sergeev11– Reference Magnusson, Gonoskov, Marklund, Esirkepov, Koga, Kondo, Kando, Bulanov, Korn, Geddes, Schroeder, Esarey and Bulanov21], as well as for studies of electron–positron plasmas[ Reference Efimenko, Bashinov, Bastrakov, Gonoskov, Muraviev, Meyerov, Kim and Sergeev22, Reference Efimenko, Bashinov, Gonoskov, Bastrakov, Muraviev, Meyerov, Kim and Sergeev23], which may help one to understand various astrophysical processes[ Reference Turolla, Zane and Watts24– Reference Kim and Kim26].
The nature of laser–matter (or laser–light) interactions is determined by several parameters, including the ratio between the electric field strength
![]() $E$
and the Schwinger, or critical, field strength
$E$
and the Schwinger, or critical, field strength
![]() ${E}_{\mathrm{cr}}={m}^2{c}^3/\left(e\mathrm{\hslash}\right)$
(where
${E}_{\mathrm{cr}}={m}^2{c}^3/\left(e\mathrm{\hslash}\right)$
(where
![]() $c$
is the speed of light,
$c$
is the speed of light,
![]() $\mathrm{\hslash}$
is the reduced Planck constant and
$\mathrm{\hslash}$
is the reduced Planck constant and
![]() $m$
and
$m$
and
![]() $e>0$
are the electron mass and charge, respectively); see also Appendix A. When
$e>0$
are the electron mass and charge, respectively); see also Appendix A. When
![]() $E/{E}_{\mathrm{cr}}\gtrsim 1$
, nonlinear quantum effects are expected to be prominent, but the way this is achieved matters. Probing a subcritical field with ultrarelativistic particles, for example, can ‘advance’ the onset of those quantum effects that depend on the rest-frame (‘r.f.’) electric field strength via the quantum nonlinearity parameter,
$E/{E}_{\mathrm{cr}}\gtrsim 1$
, nonlinear quantum effects are expected to be prominent, but the way this is achieved matters. Probing a subcritical field with ultrarelativistic particles, for example, can ‘advance’ the onset of those quantum effects that depend on the rest-frame (‘r.f.’) electric field strength via the quantum nonlinearity parameter,
![]() $\chi =\gamma E/{E}_{\mathrm{cr}}={E}_{\mathrm{r}.\mathrm{f}.}/{E}_{\mathrm{cr}}$
, with
$\chi =\gamma E/{E}_{\mathrm{cr}}={E}_{\mathrm{r}.\mathrm{f}.}/{E}_{\mathrm{cr}}$
, with
![]() $\gamma \gg 1$
being the Lorentz factor. Experimental investigation of such effects is well underway[
Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8,
Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9,
Reference Abramowicz, Acosta, Altarelli, Aßmann, Bai, Behnke, Benhammou, Blackburn, Boogert, Borysov, Borysova, Brinkmann, Bruschi, Burkart, Büßer, Cavanagh, Davidi, Decking, Dosselli, Elkina, Fedotov, Firlej, Fiutowski, Fleck, Gostkin, Grojean, Hallford, Harsh, Hartin, Heinemann, Heinzl, Helary, Hoffmann, Huang, Huang, Idzik, Ilderton, Jacobs, Kämpfer, King, Lahno, Levanon, Levy, Levy, List, Lohmann, Ma, Macleod, Malka, Meloni, Mironov, Morandin, Moron, Negodin, Perez, Pomerantz, Pöschl, Prasad, Quéré, Ringwald, Rödel, Rykovanov, Salgado, Santra, Sarri, Sävert, Sbrizzi, Schmitt, Schramm, Schuwalow, Seipt, Shaimerdenova, Shchedrolosiev, Skakunov, Soreq, Streeter, Swientek, Tal Hod, Tang, Teter, Thoden, Titov, Tolbanov, Torgrimsson, Tyazhev, Wing, Zanetti, Zarubin, Zeil, Zepf and Zhemchukov27,
Reference Yakimenko, Alsberg, Bong, Bouchard, Clarke, Emma, Green, Hast, Hogan, Seabury, Lipkowitz, O'Shea, Storey, White and Yocky28]. A different class of physical effects is manifested if we can achieve
$\gamma \gg 1$
being the Lorentz factor. Experimental investigation of such effects is well underway[
Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8,
Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9,
Reference Abramowicz, Acosta, Altarelli, Aßmann, Bai, Behnke, Benhammou, Blackburn, Boogert, Borysov, Borysova, Brinkmann, Bruschi, Burkart, Büßer, Cavanagh, Davidi, Decking, Dosselli, Elkina, Fedotov, Firlej, Fiutowski, Fleck, Gostkin, Grojean, Hallford, Harsh, Hartin, Heinemann, Heinzl, Helary, Hoffmann, Huang, Huang, Idzik, Ilderton, Jacobs, Kämpfer, King, Lahno, Levanon, Levy, Levy, List, Lohmann, Ma, Macleod, Malka, Meloni, Mironov, Morandin, Moron, Negodin, Perez, Pomerantz, Pöschl, Prasad, Quéré, Ringwald, Rödel, Rykovanov, Salgado, Santra, Sarri, Sävert, Sbrizzi, Schmitt, Schramm, Schuwalow, Seipt, Shaimerdenova, Shchedrolosiev, Skakunov, Soreq, Streeter, Swientek, Tal Hod, Tang, Teter, Thoden, Titov, Tolbanov, Torgrimsson, Tyazhev, Wing, Zanetti, Zarubin, Zeil, Zepf and Zhemchukov27,
Reference Yakimenko, Alsberg, Bong, Bouchard, Clarke, Emma, Green, Hast, Hogan, Seabury, Lipkowitz, O'Shea, Storey, White and Yocky28]. A different class of physical effects is manifested if we can achieve
![]() $E/{E}_{\mathrm{cr}}\gtrsim 1$
in the absence of massive particles, that is, directly in the laboratory frame. Such a critical field would be characterised by the invariants
$E/{E}_{\mathrm{cr}}\gtrsim 1$
in the absence of massive particles, that is, directly in the laboratory frame. Such a critical field would be characterised by the invariants
![]() ${F}^2=\left({E}^2-{c}^2{B}^2\right)/{E}_{\mathrm{cr}}^2$
and
${F}^2=\left({E}^2-{c}^2{B}^2\right)/{E}_{\mathrm{cr}}^2$
and
![]() ${G}^2= cBE/{E}_{\mathrm{cr}}^2$
, satisfying
${G}^2= cBE/{E}_{\mathrm{cr}}^2$
, satisfying
![]() $F,G\,{\gtrsim}\, 1$
. Critical and supercritical (
$F,G\,{\gtrsim}\, 1$
. Critical and supercritical (
![]() $F,G\gg 1$
) fields would modify not only the quantum dynamics of electrons and photons, but also those of heavier particles such as nuclei, and indeed the quantum electrodynamics (QED) vacuum itself.
$F,G\gg 1$
) fields would modify not only the quantum dynamics of electrons and photons, but also those of heavier particles such as nuclei, and indeed the quantum electrodynamics (QED) vacuum itself.
However, whether it is even possible to attain the needed high field strengths in the laboratory frame is an open question[ Reference Bulanov, Narozhny, Mur and Popov29– Reference Vincenti34]. This is because such fields would be expected to trigger an electron–positron pair cascade, forming a dense pair plasma that would screen or absorb the laser radiation being focused, preventing the further increase of the field strength[ Reference Fedotov, Narozhny, Mourou and Korn30, Reference Bulanov, Esirkepov, Thomas, Koga and Bulanov31, Reference Nerush, Kostyukov, Fedotov, Narozhny, Elkina and Ruhl35]. Avoiding the triggering of such a cascade (ultraintense, tightly focused lasers can ponderomotively eject stray particles that might seed a cascade, but this is dependent on the interaction geometry[ Reference Gonoskov, Gonoskov, Harvey, Ilderton, Kim, Marklund, Mourou and Sergeev32, Reference Sampath and Tamburini36]) will be essential for maximising the reachable field strength[ Reference Gonoskov, Gonoskov, Harvey, Ilderton, Kim, Marklund, Mourou and Sergeev32].
In this paper we investigate the possibility to generate supercritical fields by a combination of three essential ideas: advanced focusing, plasma-based conversion of optical or near-infrared (IR) light to extreme ultraviolet (XUV) frequencies and coherent combination of multiple laser pulses (see Figure 1). The conversion to higher frequencies has been discussed as a means of reducing the focal volume, which increases field strength at a fixed power[
Reference Baumann, Nerush, Pukhov and Kostyukov33,
Reference Vincenti34,
Reference Landecker37–
Reference Gonoskov, Korzhimanov, Kim, Marklund and Sergeev41] (a more detailed discussion can be found in Ref. [Reference Bulanov, Esirkepov, Kando, Pirozhkov and Rosanov42]). Moreover, EM processes in high-strength fields demonstrate a strong dependence on the field wavelength[
Reference Zhang, Bulanov, Seipt, Arefiev and Thomas3]. In combination with
![]() $4\pi$
focusing, which itself reduces the focal volume, this maximises the electric or magnetic field while suppressing pair cascades; see Appendix B.
$4\pi$
focusing, which itself reduces the focal volume, this maximises the electric or magnetic field while suppressing pair cascades; see Appendix B.

Figure 1 The main principle behind maximising field strength starting from laser sources with optical frequencies.
Our goal here is to provide a far-future outlook on the field strengths that could be attained in ‘best-case’ scenarios that combine currently known concepts and approaches. We demonstrate numerically that, given advanced focusing, the physics of laser–plasma interactions itself provides the possibility to reach
![]() $10{E}_{\mathrm{cr}}$
already at a laser power of 20 PW. This should certainly be seen as an idealistic (theoretical) reference point, as we omit discussion of a variety of feasibility questions, but it does indicate that further consideration and technological efforts are warranted, with the hope that
$10{E}_{\mathrm{cr}}$
already at a laser power of 20 PW. This should certainly be seen as an idealistic (theoretical) reference point, as we omit discussion of a variety of feasibility questions, but it does indicate that further consideration and technological efforts are warranted, with the hope that
![]() ${E}_{\mathrm{cr}}$
could be attained at upcoming 10-PW-class laser facilities. This would open up new and exciting opportunities for scientific discoveries, in a regime previously considered to be unattainable. Giving a complete overview of physical applications of strong fields is of course not possible, and we will restrict ourselves here to examples from electron and nuclear physics. This paper is organised as follows. Section 2 concerns the combination of the three concepts mentioned above: advanced focusing (Section 2.1), frequency upshifting through plasma-based conversion (Section 2.2) and coherent combination of multiple laser pulses (Section 2.3). Section 3 discusses the impact of such a supercritical field on nuclear and electron dynamics in Sections 3.1 and 3.2, respectively.
${E}_{\mathrm{cr}}$
could be attained at upcoming 10-PW-class laser facilities. This would open up new and exciting opportunities for scientific discoveries, in a regime previously considered to be unattainable. Giving a complete overview of physical applications of strong fields is of course not possible, and we will restrict ourselves here to examples from electron and nuclear physics. This paper is organised as follows. Section 2 concerns the combination of the three concepts mentioned above: advanced focusing (Section 2.1), frequency upshifting through plasma-based conversion (Section 2.2) and coherent combination of multiple laser pulses (Section 2.3). Section 3 discusses the impact of such a supercritical field on nuclear and electron dynamics in Sections 3.1 and 3.2, respectively.
2 Setups
In this section we provide an order of magnitude estimate for the field strength hypothetically attainable with future laser systems, with the help of the known theoretical ideas outlined above. We start by considering the concepts of
![]() $4\pi$
focusing and frequency upshifting separately, before discussing the combination of the two.
$4\pi$
focusing and frequency upshifting separately, before discussing the combination of the two.
2.1 Advanced focusing
The maximal attainable field strength for a given power of focused radiation is limited by the so-called dipole wave[
Reference Bassett43] that can also be extended to a time-limited solution known as the dipole pulse[
Reference Gonoskov, Aiello, Heugel and Leuchs44]. The dipole wave can be seen as time-reversed emission of a dipole antenna and thus can be approximated by several focused beams or by focusing an intensity-shaped radially polarised beam with a parabolic mirror[
Reference Gonoskov, Aiello, Heugel and Leuchs44,
Reference Jeong, Bulanov, Sasorov, Bulanov, Koga and Korn45]. Let us start from considering the benefits of using tight focusing of the laser radiation, characterised by small values of
![]() $f$
-number
$f$
-number
![]() ${f}_{\mathrm{N}}$
or, equivalently, by large values of the divergence angle
${f}_{\mathrm{N}}$
or, equivalently, by large values of the divergence angle
![]() $\theta =\arctan \left({f}_{\mathrm{N}}^{-1}/2\right)$
, where we for simplicity use the expression that implies
$\theta =\arctan \left({f}_{\mathrm{N}}^{-1}/2\right)$
, where we for simplicity use the expression that implies
![]() $\theta <\pi /2$
. To numerically ascertain the potential gain of using tight focusing, we set the initial EM field to be a two-cycle optical pulse propagating from a spherical surface of radius
$\theta <\pi /2$
. To numerically ascertain the potential gain of using tight focusing, we set the initial EM field to be a two-cycle optical pulse propagating from a spherical surface of radius
![]() ${r}_0\,{=}\,16\lambda$
, which can be considered large compared to the radiation wavelength
${r}_0\,{=}\,16\lambda$
, which can be considered large compared to the radiation wavelength
![]() $\lambda$
(the far-field zone):
$\lambda$
(the far-field zone):
 $$\begin{align} \mathbf{E}=\frac{\mathbf{r}\times \left[\hat{\mathbf{z}}\times \mathbf{r}\right]}{\left|\mathbf{r}\times \left[\hat{\mathbf{z}}\times \mathbf{r}\right]\right|}{S}_r\left(r+ ct\right){S}_{\alpha}\left(\alpha \right), \end{align}$$
$$\begin{align} \mathbf{E}=\frac{\mathbf{r}\times \left[\hat{\mathbf{z}}\times \mathbf{r}\right]}{\left|\mathbf{r}\times \left[\hat{\mathbf{z}}\times \mathbf{r}\right]\right|}{S}_r\left(r+ ct\right){S}_{\alpha}\left(\alpha \right), \end{align}$$
 $$\begin{align}\mathbf{B}=\frac{1}{c}\frac{\hat{\mathbf{z}}\times \mathbf{r}}{\left|\hat{\mathbf{z}}\times \mathbf{r}\right|}{S}_r\left(r+ ct\right){S}_{\alpha}\left(\alpha \right),\end{align}$$
$$\begin{align}\mathbf{B}=\frac{1}{c}\frac{\hat{\mathbf{z}}\times \mathbf{r}}{\left|\hat{\mathbf{z}}\times \mathbf{r}\right|}{S}_r\left(r+ ct\right){S}_{\alpha}\left(\alpha \right),\end{align}$$
where the radial
![]() ${S}_r(r)$
and angular
${S}_r(r)$
and angular
![]() ${S}_{\alpha}\left(\alpha \right)$
shape functions are defined by the following:
${S}_{\alpha}\left(\alpha \right)$
shape functions are defined by the following:
 $$\begin{align}{S}_r(r)=\sin \left[2\pi \left(r-{r}_0\right)/\lambda \right]\!\left\{\begin{array}{@{}ll}{\cos}^2\left[\frac{\pi }{2}\left(r-{r}_0\right)/\lambda \right],& \left|r-{r}_0\right|\le \lambda, \\ {}0,& \left|r-{r}_0\right|>\lambda, \end{array}\right.\end{align}$$
$$\begin{align}{S}_r(r)=\sin \left[2\pi \left(r-{r}_0\right)/\lambda \right]\!\left\{\begin{array}{@{}ll}{\cos}^2\left[\frac{\pi }{2}\left(r-{r}_0\right)/\lambda \right],& \left|r-{r}_0\right|\le \lambda, \\ {}0,& \left|r-{r}_0\right|>\lambda, \end{array}\right.\end{align}$$
 $$\begin{align}{S}_{\alpha}\left(\alpha \right)=\left\{\begin{array}{@{}ll}1,& \alpha \le \theta -{\theta}_{\mathrm{s}}/2,\\ {}{\sin}^2\left[\frac{\pi }{2}\left(\alpha -\theta \right)/{\theta}_\mathrm{s}\right],& \theta -{\theta}_{\mathrm{s}}/2<\alpha \le \theta +{\theta}_{\mathrm{s}}/2,\\ {}0,& \alpha >\theta +{\theta}_{\mathrm{s}}/2,\end{array}\right.\end{align}$$
$$\begin{align}{S}_{\alpha}\left(\alpha \right)=\left\{\begin{array}{@{}ll}1,& \alpha \le \theta -{\theta}_{\mathrm{s}}/2,\\ {}{\sin}^2\left[\frac{\pi }{2}\left(\alpha -\theta \right)/{\theta}_\mathrm{s}\right],& \theta -{\theta}_{\mathrm{s}}/2<\alpha \le \theta +{\theta}_{\mathrm{s}}/2,\\ {}0,& \alpha >\theta +{\theta}_{\mathrm{s}}/2,\end{array}\right.\end{align}$$
In our setup, the smoothing angle
![]() ${\theta}_{\mathrm{s}}=0.3$
eliminates the sharp edges of the concave pulse within our model. We advance this field to the vicinity of the focal point using a spectral solver of Maxwell’s equations within the open-source package hi-
${\theta}_{\mathrm{s}}=0.3$
eliminates the sharp edges of the concave pulse within our model. We advance this field to the vicinity of the focal point using a spectral solver of Maxwell’s equations within the open-source package hi-
![]() $\chi$
[
46]. To reduce the amount of needed computational resources we also employ the module of contracting a spherical window that maps the concave region of the pulse to a thin layer of space with periodic boundary conditions[
Reference Panova, Volokitin, Efimenko, Ferri, Blackburn, Marklund, Muschet, De Andres Gonzalez, Fischer, Veisz, Meyerov and Gonoskov47].
$\chi$
[
46]. To reduce the amount of needed computational resources we also employ the module of contracting a spherical window that maps the concave region of the pulse to a thin layer of space with periodic boundary conditions[
Reference Panova, Volokitin, Efimenko, Ferri, Blackburn, Marklund, Muschet, De Andres Gonzalez, Fischer, Veisz, Meyerov and Gonoskov47].
The radiation intensity at focus is proportional to the power
![]() $\mathcal{P}$
and inversely proportional to the focal spot area, which in turn scales as
$\mathcal{P}$
and inversely proportional to the focal spot area, which in turn scales as
![]() ${\lambda}^2$
, with
${\lambda}^2$
, with
![]() $\lambda$
being the radiation wavelength. It is thus possible to express the peak field strength at focus for arbitrary power
$\lambda$
being the radiation wavelength. It is thus possible to express the peak field strength at focus for arbitrary power
![]() $\mathcal{P}$
and
$\mathcal{P}$
and
![]() $\lambda$
:
$\lambda$
:
 $$\begin{align}\frac{E}{E_{\mathrm{cr}}}=\frac{\delta }{4.1\times {10}^5}\left(\frac{\lambda }{1\;\unicode{x3bc} \mathrm{m}}\right){\left(\frac{\mathcal{P}}{1\kern0.1em \mathrm{PW}}\right)}^{1/2},\end{align}$$
$$\begin{align}\frac{E}{E_{\mathrm{cr}}}=\frac{\delta }{4.1\times {10}^5}\left(\frac{\lambda }{1\;\unicode{x3bc} \mathrm{m}}\right){\left(\frac{\mathcal{P}}{1\kern0.1em \mathrm{PW}}\right)}^{1/2},\end{align}$$
where a wavelength-agnostic, dimensionless parameter
![]() $\delta$
solely characterises the efficiency of focusing. Note that we define it so that
$\delta$
solely characterises the efficiency of focusing. Note that we define it so that
![]() $\delta \sqrt{\mathcal{P}/\left(1\kern0.24em \mathrm{PW}\right)}$
gives field amplitude
$\delta \sqrt{\mathcal{P}/\left(1\kern0.24em \mathrm{PW}\right)}$
gives field amplitude
![]() $E$
in relativistic units, that is, in units of
$E$
in relativistic units, that is, in units of
![]() $mc\omega /e$
, where
$mc\omega /e$
, where
![]() $\omega$
is the radiation frequency. According to our simulations, the focusing with f/2 and f/1 provides
$\omega$
is the radiation frequency. According to our simulations, the focusing with f/2 and f/1 provides
![]() $\delta \approx 170$
and
$\delta \approx 170$
and
![]() $\delta \approx 230$
, respectively.
$\delta \approx 230$
, respectively.
A significant improvement can be achieved by splitting the power into six pulses and focusing them with
![]() ${f}_{\mathrm{N}}=1$
(
${f}_{\mathrm{N}}=1$
(
![]() $2\theta \approx 0.93<2\pi /6$
) to the same point symmetrically from different directions in the
$2\theta \approx 0.93<2\pi /6$
) to the same point symmetrically from different directions in the
![]() $x$
–
$x$
–
![]() $y$
plane, so that the polarisation vector for each pulse is orientated along the
$y$
plane, so that the polarisation vector for each pulse is orientated along the
![]() $z$
-axis. For each pulse the power is then reduced by a factor of
$z$
-axis. For each pulse the power is then reduced by a factor of
![]() $6$
and the field strength reduced by
$6$
and the field strength reduced by
![]() $\sqrt{6}$
, but the strength of the combined field multiplies this with a factor of 6 due to coherent summation of the field. As a result we have an increase by factor
$\sqrt{6}$
, but the strength of the combined field multiplies this with a factor of 6 due to coherent summation of the field. As a result we have an increase by factor
![]() $\sqrt{6}$
:
$\sqrt{6}$
:
![]() $\delta \left(6\times f/1.0\right)\approx 560$
, which is relatively close to the theoretical maximum
$\delta \left(6\times f/1.0\right)\approx 560$
, which is relatively close to the theoretical maximum
![]() ${\delta}_{\mathrm{max}}\approx 780$
provided by the dipole wave[
Reference Bassett43,
Reference Gonoskov, Aiello, Heugel and Leuchs44]. We will use this six-beam configuration as the main reference for future setups, whereas configurations with a larger number of beams can better sample the dipole wave and bring the value of
${\delta}_{\mathrm{max}}\approx 780$
provided by the dipole wave[
Reference Bassett43,
Reference Gonoskov, Aiello, Heugel and Leuchs44]. We will use this six-beam configuration as the main reference for future setups, whereas configurations with a larger number of beams can better sample the dipole wave and bring the value of
![]() $\delta$
even closer to
$\delta$
even closer to
![]() ${\delta}_{\mathrm{max}}$
.
${\delta}_{\mathrm{max}}$
.
The maximal field strength is achieved either for the electric or magnetic field component (pointing along the
![]() $z$
-axis), whereas the other field component is close to zero in the centre. The maximisation of the electric field with the so-called electric dipole wave provides a strong, oscillating electric field that is especially interesting for enhancing the production of electrons and positrons, as well as for trapping them by anomalous radiative trapping[
Reference Gonoskov, Bashinov, Gonoskov, Harvey, Ilderton, Kim, Marklund, Mourou and Sergeev11], which in combination provides a unique condition for the creation of radiation sources[
Reference Gonoskov, Bashinov, Bastrakov, Efimenko, Ilderton, Kim, Marklund, Meyerov, Muraviev and Sergeev14] and extreme plasma states[
Reference Efimenko, Bashinov, Bastrakov, Gonoskov, Muraviev, Meyerov, Kim and Sergeev22,
Reference Efimenko, Bashinov, Gonoskov, Bastrakov, Muraviev, Meyerov, Kim and Sergeev23]. The maximisation of the magnetic field by the magnetic dipole wave can also be of interest for initiating extreme plasma dynamics[
Reference Bashinov, Efimenko, Muraviev, Volokitin, Meyerov, Leuchs, Sergeev and Kim48] as well as for reaching strong fields with suppressed EM cascades in the centre. The interaction of an optical dipole wave with a high-energy electron beam leads to the generation of multi-GeV photon sources and can be used as a platform for the study of EM cascades, of both shower and avalanche types[
Reference Magnusson, Gonoskov, Marklund, Esirkepov, Koga, Kondo, Kando, Bulanov, Korn and Bulanov20,
Reference Magnusson, Gonoskov, Marklund, Esirkepov, Koga, Kondo, Kando, Bulanov, Korn, Geddes, Schroeder, Esarey and Bulanov21]. Finally, a symmetric mixture of electric and magnetic dipole waves provides the optimal setup for attaining the highest possible
$z$
-axis), whereas the other field component is close to zero in the centre. The maximisation of the electric field with the so-called electric dipole wave provides a strong, oscillating electric field that is especially interesting for enhancing the production of electrons and positrons, as well as for trapping them by anomalous radiative trapping[
Reference Gonoskov, Bashinov, Gonoskov, Harvey, Ilderton, Kim, Marklund, Mourou and Sergeev11], which in combination provides a unique condition for the creation of radiation sources[
Reference Gonoskov, Bashinov, Bastrakov, Efimenko, Ilderton, Kim, Marklund, Meyerov, Muraviev and Sergeev14] and extreme plasma states[
Reference Efimenko, Bashinov, Bastrakov, Gonoskov, Muraviev, Meyerov, Kim and Sergeev22,
Reference Efimenko, Bashinov, Gonoskov, Bastrakov, Muraviev, Meyerov, Kim and Sergeev23]. The maximisation of the magnetic field by the magnetic dipole wave can also be of interest for initiating extreme plasma dynamics[
Reference Bashinov, Efimenko, Muraviev, Volokitin, Meyerov, Leuchs, Sergeev and Kim48] as well as for reaching strong fields with suppressed EM cascades in the centre. The interaction of an optical dipole wave with a high-energy electron beam leads to the generation of multi-GeV photon sources and can be used as a platform for the study of EM cascades, of both shower and avalanche types[
Reference Magnusson, Gonoskov, Marklund, Esirkepov, Koga, Kondo, Kando, Bulanov, Korn and Bulanov20,
Reference Magnusson, Gonoskov, Marklund, Esirkepov, Koga, Kondo, Kando, Bulanov, Korn, Geddes, Schroeder, Esarey and Bulanov21]. Finally, a symmetric mixture of electric and magnetic dipole waves provides the optimal setup for attaining the highest possible
![]() $\chi$
value for a given external beam of high-energy electrons[
Reference Olofsson and Gonoskov49]. Here we proceed with our analysis for the electric dipole wave.
$\chi$
value for a given external beam of high-energy electrons[
Reference Olofsson and Gonoskov49]. Here we proceed with our analysis for the electric dipole wave.
2.2 Plasma converter
The idea and particular concepts for field intensification through plasma-based high-order harmonic generation and focusing have been being discussed by several research groups since the beginning of the 2000s. One possibility is to use Doppler frequency upshifting during the reflection of laser radiation from so-called relativistic flying mirrors formed either by the cusp of the preceding plasma wave breaking[
Reference Bulanov, Esirkepov and Tajima38,
Reference Martins, Santos, Fonseca and Silva50,
Reference Matlis, Reed, Bulanov, Chvykov, Kalintchenko, Matsuoka, Rousseau, Yanovsky, Maksimchuk, Kalmykov, Shvets and Downer51] or by the ejection of electrons from thin plasma layers[
Reference Kulagin, Cherepenin, Hur and Suk52–
Reference Esirkepov, Bulanov, Kando, Pirozhkov and Zhidkov56]. In both cases a counter-propagating laser pulse is used to produce the flying mirror that can be shaped to focus the reflected radiation. Another possibility is to use the highly nonlinear reflection of laser radiation from dense plasma naturally formed by the ionisation of solid targets[
Reference Bulanov, Naumova and Pegoraro57–
Reference von der Linde and Rzàzewski59]. The early discussions and models also appealed to the Doppler frequency upshifting, which in this case occurs during the reflection from the oscillating effective boundary[
Reference Gordienko, Pukhov, Shorokhov and Baeva60,
Reference Baeva, Gordienko and Pukhov61] that can also be shaped for harmonic focusing by tailoring the pulse intensity shape[
Reference Naumova, Nees, Sokolov, Hou and Mourou39,
Reference Dromey, Adams, Hörlein, Nomura, Rykovanov, Carroll, Foster, Kar, Markey, McKenna, Neely, Geissler, Tsakiris and Zepf62] . It was later recognised that the conversion can be more generally seen as coherent synchrotron emission (CSE) of electrons from a self-generated peripheral layer of electrons[
Reference Der Brügge and Pukhov63], while the layer’s spring-like dynamics and sought-after emission can be described by a set of differential equations forming the so-called relativistic electronic spring (RES) model[
Reference Gonoskov, Korzhimanov, Kim, Marklund and Sergeev41,
Reference Gonoskov64,
Reference Blanco, Flores-Arias and Gonoskov65]. Further studies[
Reference Blackburn, Gonoskov and Marklund66] showed that optimal conversion is achievable with an incidence angle of
![]() $50{}^{\circ}{-}62{}^{\circ}$
and the density ramps are achievable via tailored pulse contrast[
Reference Rödel, an der Brügge, Bierbach, Yeung, Hahn, Dromey, Herzer, Fuchs, Pour, Eckner, Behmke, Cerchez, Jäckel, Hemmers, Toncian, Kaluza, Belyanin, Pretzler, Willi, Pukhov, Zepf and Paulus67]. The latest numerical studies exploiting plasma denting in combination with oblique incidence indicate the possibility of significant field intensification[
Reference Baumann, Nerush, Pukhov and Kostyukov33,
Reference Vincenti34]. Some of the reported numerical results are summarised in Table 1. As a way to estimate future prospects, we consider the conversion described in Refs. [Reference Gonoskov, Korzhimanov, Kim, Marklund and Sergeev41,Reference Der Brügge and Pukhov63].
$50{}^{\circ}{-}62{}^{\circ}$
and the density ramps are achievable via tailored pulse contrast[
Reference Rödel, an der Brügge, Bierbach, Yeung, Hahn, Dromey, Herzer, Fuchs, Pour, Eckner, Behmke, Cerchez, Jäckel, Hemmers, Toncian, Kaluza, Belyanin, Pretzler, Willi, Pukhov, Zepf and Paulus67]. The latest numerical studies exploiting plasma denting in combination with oblique incidence indicate the possibility of significant field intensification[
Reference Baumann, Nerush, Pukhov and Kostyukov33,
Reference Vincenti34]. Some of the reported numerical results are summarised in Table 1. As a way to estimate future prospects, we consider the conversion described in Refs. [Reference Gonoskov, Korzhimanov, Kim, Marklund and Sergeev41,Reference Der Brügge and Pukhov63].
Table 1 Some of the reported numerical results on focusing plasma-generated XUV pulses.

We performed a number of simulations using a 1D version of the ELMIS PIC code[
Reference Gonoskov68] with the quantum radiation reaction accounted for via the QED event generator described in Ref. [Reference Gonoskov, Bastrakov, Efimenko, Ilderton, Marklund, Meyerov, Muraviev, Sergeev, Surmin and Wallin69]. (The oblique incidence is transformed to normal in a moving reference frame[
Reference Bourdier70].) We assumed a single-cycle laser pulse (
![]() $\lambda =0.81\kern0.22em \unicode{x3bc} \mathrm{m}$
) interacting with a steep-front plasma surface with immobile ions. Many factors, including, for example, the motion of ions, plasma spreading due to limited contrast and the pulse shape, can significantly affect both the increase of the amplitude and the optimal conditions for achieving it. However, the physics of this process has been shown to be sufficiently robust to justify the considerations here as a good starting point for further studies[
Reference Gonoskov64,
Reference Blackburn, Gonoskov and Marklund66,
Reference Bhadoria, Blackburn, Gonoskov and Marklund71].
$\lambda =0.81\kern0.22em \unicode{x3bc} \mathrm{m}$
) interacting with a steep-front plasma surface with immobile ions. Many factors, including, for example, the motion of ions, plasma spreading due to limited contrast and the pulse shape, can significantly affect both the increase of the amplitude and the optimal conditions for achieving it. However, the physics of this process has been shown to be sufficiently robust to justify the considerations here as a good starting point for further studies[
Reference Gonoskov64,
Reference Blackburn, Gonoskov and Marklund66,
Reference Bhadoria, Blackburn, Gonoskov and Marklund71].
The amplitude increase becomes larger with the increase of incident wave amplitude
![]() ${a}_{\mathrm{in}}$
, which we express in relativistic units[
Reference Bashinov, Gonoskov, Kim, Mourou and Sergeev72]. We consider two cases
${a}_{\mathrm{in}}$
, which we express in relativistic units[
Reference Bashinov, Gonoskov, Kim, Mourou and Sergeev72]. We consider two cases
![]() ${a}_{\mathrm{in}}\approx 70$
(
${a}_{\mathrm{in}}\approx 70$
(
![]() ${I={10}^{22}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2}$
) and
${I={10}^{22}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2}$
) and
![]() ${a}_{\mathrm{in}}\approx 220$
(
${a}_{\mathrm{in}}\approx 220$
(
![]() $I={10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
). For each case we fine tune the incidence angle
$I={10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
). For each case we fine tune the incidence angle
![]() $\alpha$
and the plasma density
$\alpha$
and the plasma density
![]() $n$
expressed in units of plasma critical density. For
$n$
expressed in units of plasma critical density. For
![]() $I={10}^{22}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
we find that the maximal amplitude increase of
$I={10}^{22}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
we find that the maximal amplitude increase of
![]() $8.4$
is achieved for
$8.4$
is achieved for
![]() $\alpha =61.43{}^{\circ}$
and
$\alpha =61.43{}^{\circ}$
and
![]() $n=0.4125{a}_{\mathrm{in}}$
, whereas for
$n=0.4125{a}_{\mathrm{in}}$
, whereas for
![]() $I={10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
the maximal amplitude increase of
$I={10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
the maximal amplitude increase of
![]() $16.1$
is achieved for the same incidence angle but for
$16.1$
is achieved for the same incidence angle but for
![]() $n=0.397{a}_{\mathrm{in}}$
. For the latter, the resulting field distribution is shown in Figure 2(b). The length of the generated pulses in these cases is less than 1 nm, which corresponds to the XUV range.
$n=0.397{a}_{\mathrm{in}}$
. For the latter, the resulting field distribution is shown in Figure 2(b). The length of the generated pulses in these cases is less than 1 nm, which corresponds to the XUV range.

Figure 2 (a) The numerical result for the dipole focusing of XUV pulse. (b) The total laser power of 200 PW is split into six beams and each is focused to
![]() ${10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
at
${10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
at
![]() $7\kern0.22em \unicode{x3bc} \mathrm{m}$
from the focus, where the plasma converters provide an amplitude boost by a factor of 15 and frequency upshift by a factor of approximately
$7\kern0.22em \unicode{x3bc} \mathrm{m}$
from the focus, where the plasma converters provide an amplitude boost by a factor of 15 and frequency upshift by a factor of approximately
![]() ${10}^4$
. The conversion is followed by the MCLP (e-dipole) focusing using six beams at
${10}^4$
. The conversion is followed by the MCLP (e-dipole) focusing using six beams at
![]() $f/1.0$
. (c) The dependency of the field strength on the
$f/1.0$
. (c) The dependency of the field strength on the
![]() $x$
-coordinate (green curve),
$x$
-coordinate (green curve),
![]() $z$
-coordinate (blue curve) and time (red curve) is shown in panel (c) together with the fit (black solid curves) and the threshold for cascaded pair-generation (dashed black line).
$z$
-coordinate (blue curve) and time (red curve) is shown in panel (c) together with the fit (black solid curves) and the threshold for cascaded pair-generation (dashed black line).
Although our goal here is to assess the capabilities of the conversion physics itself, we do not consider higher incident intensities, even though these could lead to even higher intensification factors and even shorter pulse duration. One reason for this is that, at higher intensities, QED effects can start to play a detrimental role, due to an increasingly large part of the incident energy being converted into gamma photons (see Ref. [Reference Nerush, Kostyukov, Ji and Pukhov73] and Fig. 2 in Ref. [Reference Gonoskov, Bastrakov, Efimenko, Ilderton, Marklund, Meyerov, Muraviev, Sergeev, Surmin and Wallin69]). Ion motion is another factor that becomes more prominent with the rise of intensity and makes it difficult to efficiently exploit the conversion mechanism. This motivates further studies on the generation of short pulses[
Reference Rivas, Borot, Cardenas, Marcus, Gu, Herrmann, Xu, Tan, Kormin, Ma, Dallari, Tsakiris, Földes, Chou, Weidman, Bergues, Wittmann, Schröder, Tzallas, Charalambidis, Razskazovskaya, Pervak, Krausz and Veisz74], exploiting pulse steepening[
Reference Gustafson, Taran, Haus, Lifsitz and Kelley75–
Reference Wang, Lin, Sheng, Liu, Zhao, Guo, Lu, He, Chen and Yan79] and possibilities to use high-
![]() $Z$
, that is, heavy nuclei, material (note that a higher intensity can cause almost complete ionisation, making the charge-to-mass ratio close to
$Z$
, that is, heavy nuclei, material (note that a higher intensity can cause almost complete ionisation, making the charge-to-mass ratio close to
![]() $e/2{m}_p$
independent of the nuclei type). Finally, for a given incident power, higher intensity at the converter means a smaller area of conversion. Once the characteristic size of the conversion area
$e/2{m}_p$
independent of the nuclei type). Finally, for a given incident power, higher intensity at the converter means a smaller area of conversion. Once the characteristic size of the conversion area
![]() ${r}_0/\left(1\;\unicode{x3bc} \mathrm{m}\right)\sim {\left(P/\mathrm{PW}\right)}^{1/2}{\left[I/\left({10}^{22}\;{\mathrm{W\,cm}}^{-2}\right)\right]}^{-1/2}$
becomes comparable to the wavelength
${r}_0/\left(1\;\unicode{x3bc} \mathrm{m}\right)\sim {\left(P/\mathrm{PW}\right)}^{1/2}{\left[I/\left({10}^{22}\;{\mathrm{W\,cm}}^{-2}\right)\right]}^{-1/2}$
becomes comparable to the wavelength
![]() $\lambda \sim 1\;\unicode{x3bc}$
m, multidimensional effects start to affect both the conversion process itself and the collimation and synchronisation of the XUV pulses generated across the focal area (for 2D numerical studies of the plasma conversion by the considered mechanism see Refs. [Reference Blackburn, Gonoskov and Marklund66,Reference Bhadoria, Blackburn, Gonoskov and Marklund71]). In this context and for
$\lambda \sim 1\;\unicode{x3bc}$
m, multidimensional effects start to affect both the conversion process itself and the collimation and synchronisation of the XUV pulses generated across the focal area (for 2D numerical studies of the plasma conversion by the considered mechanism see Refs. [Reference Blackburn, Gonoskov and Marklund66,Reference Bhadoria, Blackburn, Gonoskov and Marklund71]). In this context and for
![]() $I={10}^{22}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
the minimal power is a few PW, whereas for
$I={10}^{22}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
the minimal power is a few PW, whereas for
![]() $I={10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
, it is preferable to have a few tens of PW.
$I={10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
, it is preferable to have a few tens of PW.
2.3 Focusing of XUV pulses
We now continue our analysis by considering the possibility of focusing the XUV pulses generated at the curved plasma surfaces of the six focusing mirrors with
![]() ${f}_{\mathrm{N}}=1$
. We assume that the laser radiation is split into six beams, pre-focused and delivered so that the optimal conditions for the plasma converters are achieved at the plasma surfaces and the generated XUV pulses become focused at the central point. We assume that the conversion happens at the distance of 6 μm from the centre. We consider two cases: the total power
${f}_{\mathrm{N}}=1$
. We assume that the laser radiation is split into six beams, pre-focused and delivered so that the optimal conditions for the plasma converters are achieved at the plasma surfaces and the generated XUV pulses become focused at the central point. We assume that the conversion happens at the distance of 6 μm from the centre. We consider two cases: the total power
![]() $\mathcal{P}$
is 20 and 200 PW, which results in the intensities of
$\mathcal{P}$
is 20 and 200 PW, which results in the intensities of
![]() ${10}^{22}\kern0.1em$
and
${10}^{22}\kern0.1em$
and
![]() ${10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
at the plasma surfaces, respectively. A rough estimate for the peak field strength achievable in this configuration suggests that for
${10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
at the plasma surfaces, respectively. A rough estimate for the peak field strength achievable in this configuration suggests that for
![]() $\mathcal{P}=20\kern0.22em \mathrm{PW}$
(200 PW) we can reach
$\mathcal{P}=20\kern0.22em \mathrm{PW}$
(200 PW) we can reach
![]() ${a}_{\mathrm{out}}\sim 2500$
(8000) given in relativistic units for the wavelength
${a}_{\mathrm{out}}\sim 2500$
(8000) given in relativistic units for the wavelength
![]() $\lambda \sim 1\kern0.1em \mathrm{nm}$
, which is well above the Schwinger field strength in both cases. However, this estimate is not sufficient because different spectral fractions are focused to different diffraction-limited volumes. That is why we need to perform numerical calculation to realize estimations for these cases.
$\lambda \sim 1\kern0.1em \mathrm{nm}$
, which is well above the Schwinger field strength in both cases. However, this estimate is not sufficient because different spectral fractions are focused to different diffraction-limited volumes. That is why we need to perform numerical calculation to realize estimations for these cases.
In order to resolve the singular XUV peak we use a sequence of adaptive sub-grids that are arranged in the following way. First, we surround the XUV peak with a frame and deduce there the field multiplying by a mask function that smoothly goes from 1 to 0 and the ends of the frame. In such a way we cut out the XUV pulse, and the remaining field with narrower spectral content can be sampled with the first grid. We then take the deduced field within the frame and repeat the procedure, introducing another subframe in a closer vicinity of the XUV peak and sampling the remaining field with another thinner sub-grid. We perform this procedure seven times to reach a sufficient resolution, which in our case corresponds to the space step of 0.064 nm. Every deduced field is advanced first analytically (as a spherical wave) to the distance of four frame lengths and then numerically using the spectral solver on the grid 128 × 5122.
The result of our numerical calculation for
![]() $\mathcal{P}=200\kern0.22em \mathrm{PW}$
is shown in Figure 2. The peak field of 130
$\mathcal{P}=200\kern0.22em \mathrm{PW}$
is shown in Figure 2. The peak field of 130
![]() ${E}_{\mathrm{cr}}$
is achieved in the centre within a volume of about a few nanometres in size. The following fit can be used for estimates and calculations:
${E}_{\mathrm{cr}}$
is achieved in the centre within a volume of about a few nanometres in size. The following fit can be used for estimates and calculations:
 $$\begin{align}\frac{E\left(r,t\right)}{E_{\mathrm{cr}}}\approx \mathcal{A}{\left({\left|\frac{r+ ct}{R}\right|}^{3/2}+1\right)}^{-1}{\left(\left|\frac{ct}{D}\right|+1\right)}^{-1},\end{align}$$
$$\begin{align}\frac{E\left(r,t\right)}{E_{\mathrm{cr}}}\approx \mathcal{A}{\left({\left|\frac{r+ ct}{R}\right|}^{3/2}+1\right)}^{-1}{\left(\left|\frac{ct}{D}\right|+1\right)}^{-1},\end{align}$$
where
![]() $\mathcal{A}=130$
,
$\mathcal{A}=130$
,
![]() $R=0.2\kern0.22em \mathrm{nm}$
and
$R=0.2\kern0.22em \mathrm{nm}$
and
![]() $D=0.3\kern0.22em \mathrm{nm}$
in this case (see the solid black curves in Figure 2(c)). A similar result is obtained for the case of
$D=0.3\kern0.22em \mathrm{nm}$
in this case (see the solid black curves in Figure 2(c)). A similar result is obtained for the case of
![]() $\mathcal{P}=20\kern0.22em \mathrm{PW}$
, for which we got best fit for
$\mathcal{P}=20\kern0.22em \mathrm{PW}$
, for which we got best fit for
![]() $\mathcal{A}=10$
,
$\mathcal{A}=10$
,
![]() $R=0.5\kern0.22em \mathrm{nm}$
and
$R=0.5\kern0.22em \mathrm{nm}$
and
![]() $D=0.5\kern0.22em \mathrm{nm}$
.
$D=0.5\kern0.22em \mathrm{nm}$
.
The threshold for the cascade can be estimated as the equality of the volume size (distance to the centre) to the mean scale length of pair production. This estimate is shown in Figure 2(c) with a dashed black line and indicates that the region where the field reaches
![]() ${E}_{\mathrm{s}}$
is too small for the occurrence of the cascade based on the Breit–Wheeler process.
${E}_{\mathrm{s}}$
is too small for the occurrence of the cascade based on the Breit–Wheeler process.
We conclude this section by showing schematically the potential of reaching strong fields with different strategies based on a given value of the total laser power of a laser facility (see Figure 3). One can see that using tight focusing or, better still, multiple colliding laser pulses (MCLPs)[
Reference Bulanov, Mur, Narozhny, Nees and Popov80], provides a substantial increase of the peak field, which is, however, well below the Schwinger field even in case of 1 EW total power. The plasma converter can give a significant increase once the intensity of
![]() ${10}^{22}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
is reached, which can be provided by
${10}^{22}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
is reached, which can be provided by
![]() $f/1.0$
focusing already with the total laser power of about 100 TW. The conversion at
$f/1.0$
focusing already with the total laser power of about 100 TW. The conversion at
![]() ${10}^{23}\kern0.1em \mathrm{W}/\mathrm{cm}^{2}$
provides an even larger boost. In both cases, tight focusing of the generated XUV pulses can provide a significant increase of field strength beyond
${10}^{23}\kern0.1em \mathrm{W}/\mathrm{cm}^{2}$
provides an even larger boost. In both cases, tight focusing of the generated XUV pulses can provide a significant increase of field strength beyond
![]() ${E}_{\mathrm{cr}}$
.
${E}_{\mathrm{cr}}$
.

Figure 3 The prospects of reaching high field strength using tight focusing, multiple laser colliding pulses, the plasma conversion and their combination on the map of the attainable field strength and total power of the laser facility. The two outlined options correspond to the use of the plasma conversion at
![]() ${10}^{22}$
and
${10}^{22}$
and
![]() ${10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
, respectively. The labels show the results of simulations by Gonoskov et al. [
Reference Gonoskov, Korzhimanov, Kim, Marklund and Sergeev41] (1), by Baumann et al. [
Reference Baumann, Nerush, Pukhov and Kostyukov33] (2) and by Vincenti[
Reference Vincenti34] (3).
${10}^{23}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
, respectively. The labels show the results of simulations by Gonoskov et al. [
Reference Gonoskov, Korzhimanov, Kim, Marklund and Sergeev41] (1), by Baumann et al. [
Reference Baumann, Nerush, Pukhov and Kostyukov33] (2) and by Vincenti[
Reference Vincenti34] (3).
Certainly, this analysis is performed under the assumption of the best-case scenario and the implementation of such a concept requires many technological advances. Among them, driving plasma conversion and reaching spatial-temporal synchronisation of the generated XUV pulses appear to the central difficulties. However, from our results we can draw a conclusion that achieving the needed spatio-temporal control in the domain of nanometre-attosecond could provide a pathway towards reaching the Schwinger field strength using the outlined concept based on high-intensity laser facilities.
We estimate that delivering 10 GeV electrons to the strong-field region of the outlined setup would result in a
![]() $\chi$
of order
$\chi$
of order
![]() ${10}^6$
for the case of
${10}^6$
for the case of
![]() $\mathcal{P}=20$
PW (see estimates in Appendix B). We will investigate such possibilities in future work.
$\mathcal{P}=20$
PW (see estimates in Appendix B). We will investigate such possibilities in future work.
3 Physical processes in critical and supercritical fields
Critical and supercritical fields open up the possibility to perform experiments in regimes that traditionally have not been available to light sources. For the purpose of illustration, we briefly discuss a number of possible studies that could be performed using the extreme-field source we have outlined.
3.1 Nuclear dynamics
Studies of nuclear photonics have been strongly motivated by using high-brilliance gamma sources for, for example, excitation of nuclei. However, strong EM fields can also reach the scales relevant for probing internal nuclear dynamics. Before going further with some examples, we point out that these experiments would give rise to significant challenges, such as the alignment of the target with the focal spot, as well as timing issues. It is still of interest to consider these possibilities, because solid-density plasma can be transparent for the high-intensity XUV pulses. It might also be possible to deliver accelerated nuclei to focus along the dipole pulse axis, where the field strength is greatly suppressed[ Reference Magnusson, Gonoskov, Marklund, Esirkepov, Koga, Kondo, Kando, Bulanov, Korn and Bulanov20]. In this case, it might be necessary to accumulate the signal of repeated experiments to compensate for the small size of the strong-field region. To motivate further studies on possible experimental arrangements we discuss some of the possibilities that arise in nuclear physics through the development of strong-field sources.
Electric fields of the strength discussed in Section 2 are sufficient to strip atoms of their electrons; the field strength necessary for barrier-suppression ionisation of the deepest lying electron is
![]() ${E}_{\mathrm{BSI}}\simeq {\left( Z\alpha \right)}^3{E}_{\mathrm{cr}}/16$
. The bare nucleus can then be accelerated to relativistic velocity, in a single wave period, if the electric field amplitude
${E}_{\mathrm{BSI}}\simeq {\left( Z\alpha \right)}^3{E}_{\mathrm{cr}}/16$
. The bare nucleus can then be accelerated to relativistic velocity, in a single wave period, if the electric field amplitude
![]() $E>{E}_{\mathrm{rel}}$
, where
$E>{E}_{\mathrm{rel}}$
, where
and
![]() $Z$
and
$Z$
and
![]() $A$
are the nucleus’ atomic and mass numbers, respectively. Thus, the source of a near-critical field could accelerate heavy nuclei from rest to normalised momentum,
$A$
are the nucleus’ atomic and mass numbers, respectively. Thus, the source of a near-critical field could accelerate heavy nuclei from rest to normalised momentum,
![]() $p/M=225\left(Z/A\right)\left(E/{E}_{\mathrm{cr}}\right)\lambda \left[\unicode{x3bc} \mathrm{m}\right]\gg 1$
.
$p/M=225\left(Z/A\right)\left(E/{E}_{\mathrm{cr}}\right)\lambda \left[\unicode{x3bc} \mathrm{m}\right]\gg 1$
.
Stronger electric fields affect even the internal dynamics of the nucleus, by modifying the Coulomb barrier through which daughter particles tunnel. For example, the characteristic electric field required to modify the
![]() $\alpha$
-decay rate of an unstable nucleus,
$\alpha$
-decay rate of an unstable nucleus,
![]() ${E}_{\alpha }$
, can be estimated as follows[
Reference Pálffy and Popruzhenko81]:
${E}_{\alpha }$
, can be estimated as follows[
Reference Pálffy and Popruzhenko81]:
 $$\begin{align}\frac{E_{\alpha }}{E_{\mathrm{cr}}}=\frac{2\sqrt{2}{Q}_{\alpha}^{5/2}}{3{\pi \alpha}^2{Z}^2{Z}_{\mathrm{eff}}{m}_{\mathrm{e}}^2{m}_{\mathrm{r}}^{1/2}}\simeq 300\kern0.1em \frac{Q^{5/2}\left[\mathrm{MeV}\right]}{Z^2{Z}_{\mathrm{eff}}},\end{align}$$
$$\begin{align}\frac{E_{\alpha }}{E_{\mathrm{cr}}}=\frac{2\sqrt{2}{Q}_{\alpha}^{5/2}}{3{\pi \alpha}^2{Z}^2{Z}_{\mathrm{eff}}{m}_{\mathrm{e}}^2{m}_{\mathrm{r}}^{1/2}}\simeq 300\kern0.1em \frac{Q^{5/2}\left[\mathrm{MeV}\right]}{Z^2{Z}_{\mathrm{eff}}},\end{align}$$
where
![]() $Q$
is the energy of the
$Q$
is the energy of the
![]() $\alpha$
particle,
$\alpha$
particle,
![]() ${Z}_{\mathrm{eff}}=\left(2A-4Z\right)/\left(A+4\right)$
,
${Z}_{\mathrm{eff}}=\left(2A-4Z\right)/\left(A+4\right)$
,
![]() $Z$
and
$Z$
and
![]() $A$
are the proton and mass numbers of the daughter nucleus, respectively, and
$A$
are the proton and mass numbers of the daughter nucleus, respectively, and
![]() ${m}_{\mathrm{r}}$
is the reduced mass of the
${m}_{\mathrm{r}}$
is the reduced mass of the
![]() $\alpha$
–daughter-nucleus system. For polonium-
$\alpha$
–daughter-nucleus system. For polonium-
![]() $212$
, which has a half-life of
$212$
, which has a half-life of
![]() $0.3$
ms,
$0.3$
ms,
![]() $Q\simeq 9.0$
MeV and
$Q\simeq 9.0$
MeV and
![]() ${E}_{\alpha }/{E}_{\mathrm{cr}}\simeq 30$
. The correction to the decay rate
${E}_{\alpha }/{E}_{\mathrm{cr}}\simeq 30$
. The correction to the decay rate
![]() $C=\exp \left[2E(t)\cos \theta /{E}_{\alpha}\right]$
, where
$C=\exp \left[2E(t)\cos \theta /{E}_{\alpha}\right]$
, where
![]() $\theta$
is the angle between the electric field vector and the
$\theta$
is the angle between the electric field vector and the
![]() $\alpha$
-emission direction. Averaging over all
$\alpha$
-emission direction. Averaging over all
![]() $\theta$
, we obtain
$\theta$
, we obtain
![]() ${\left\langle C\right\rangle}_{\theta}=\sinh \left[2E(t)/{E}_{\alpha}\right]/\left[2E(t)/{E}_{\alpha}\right]$
. Further averaged over a single cycle, with
${\left\langle C\right\rangle}_{\theta}=\sinh \left[2E(t)/{E}_{\alpha}\right]/\left[2E(t)/{E}_{\alpha}\right]$
. Further averaged over a single cycle, with
![]() $E(t)={E}_0\sin \omega t$
, we find that the modification to the decay rate is
$E(t)={E}_0\sin \omega t$
, we find that the modification to the decay rate is
![]() ${\left\langle C\right\rangle}_{\theta, t}\simeq 1.4$
for
${\left\langle C\right\rangle}_{\theta, t}\simeq 1.4$
for
![]() ${E}_0=30{E}_{\mathrm{cr}}$
and as much as
${E}_0=30{E}_{\mathrm{cr}}$
and as much as
![]() ${\left\langle C\right\rangle}_{\theta, t}\simeq 21$
for
${\left\langle C\right\rangle}_{\theta, t}\simeq 21$
for
![]() ${E}_0=100{E}_{\mathrm{cr}}$
. We note that by exceeding
${E}_0=100{E}_{\mathrm{cr}}$
. We note that by exceeding
![]() ${E}_{\alpha }$
we enter a regime where the effect of the external field is no longer a small correction.
${E}_{\alpha }$
we enter a regime where the effect of the external field is no longer a small correction.
The same logic can be applied to
![]() $\beta$
decay, where the characteristic electric field required to modify the decay rate is as follows[
Reference Akhmedov82]:
$\beta$
decay, where the characteristic electric field required to modify the decay rate is as follows[
Reference Akhmedov82]:
 $$\begin{align}\frac{E_{\beta }}{E_{\mathrm{cr}}}={\left(\frac{2{Q}_{\beta }}{m_{\mathrm{e}}}\right)}^{3/2},\end{align}$$
$$\begin{align}\frac{E_{\beta }}{E_{\mathrm{cr}}}={\left(\frac{2{Q}_{\beta }}{m_{\mathrm{e}}}\right)}^{3/2},\end{align}$$
where
![]() ${Q}_{\beta }$
is the energy release associated with the decay. In the case of tritium,
${Q}_{\beta }$
is the energy release associated with the decay. In the case of tritium,
![]() ${Q}_{\beta}=18.6$
keV and
${Q}_{\beta}=18.6$
keV and
![]() ${E}_{\beta}=0.02{E}_{\mathrm{cr}}$
. As this is a non-relativistic beta decay,
${E}_{\beta}=0.02{E}_{\mathrm{cr}}$
. As this is a non-relativistic beta decay,
![]() ${Q}_{\beta }/m\ll 1$
, the modification to the decay rate is
${Q}_{\beta }/m\ll 1$
, the modification to the decay rate is
![]() $C\simeq {\left({E}_0/{E}_{\beta}\right)}^{7/3}$
for an applied electric field
$C\simeq {\left({E}_0/{E}_{\beta}\right)}^{7/3}$
for an applied electric field
![]() ${E}_0$
, which satisfies
${E}_0$
, which satisfies
![]() ${E}_0/{E}_{\beta}\gg 1$
[
Reference Akhmedov82]: at
${E}_0/{E}_{\beta}\gg 1$
[
Reference Akhmedov82]: at
![]() ${E}_0=0.1{E}_{\mathrm{cr}}$
,
${E}_0=0.1{E}_{\mathrm{cr}}$
,
![]() $C\simeq 50$
.
$C\simeq 50$
.
3.2 Electron dynamics
A supercritical field structure of this type is a platform for investigating nonlinear QED in a completely unexplored regime, either by probing it with externally injected electrons or by exploiting the nonlinear dynamics of virtual particles from the quantum vacuum.
Based on an analysis of quantum loop corrections to physical processes in constant, crossed fields, it has been conjectured that the relevant expansion parameter is not the fine structure constant
![]() $\alpha$
, small, but rather
$\alpha$
, small, but rather
![]() ${\alpha \chi}^{2/3}$
, which can become large in extremely strong fields[
Reference Ritus83,
Reference Narozhny84]. Hence, the usual small expansion parameter of perturbative QED becomes, in principle, a large parameter for
${\alpha \chi}^{2/3}$
, which can become large in extremely strong fields[
Reference Ritus83,
Reference Narozhny84]. Hence, the usual small expansion parameter of perturbative QED becomes, in principle, a large parameter for
![]() $\chi >1600$
. In a collision between an electron beam of energy
$\chi >1600$
. In a collision between an electron beam of energy
![]() $\mathrm{\mathcal{E}}$
and a supercritical electric field of magnitude
$\mathrm{\mathcal{E}}$
and a supercritical electric field of magnitude
![]() $E$
, we have the following:
$E$
, we have the following:
 $$\begin{align}{\alpha \chi}^{2/3}=5.3\kern0.1em {\mathrm{\mathcal{E}}}^{2/3}\left[10\,\mathrm{GeV}\right]{\left(\frac{E}{E_{\mathrm{cr}}}\right)}^{2/3}.\end{align}$$
$$\begin{align}{\alpha \chi}^{2/3}=5.3\kern0.1em {\mathrm{\mathcal{E}}}^{2/3}\left[10\,\mathrm{GeV}\right]{\left(\frac{E}{E_{\mathrm{cr}}}\right)}^{2/3}.\end{align}$$
Higher-order corrections, normally thought of as suppressed by powers of
![]() $\alpha$
, are implied by the conjecture to become larger and larger as the order increases. The technical implication is that the perturbative expansion of QED breaks down and needs (somehow) to be re-summed[
Reference Heinzl, Ilderton and King85]; the physical implication is that QED enters a new ‘fully nonperturbative’ regime in which it behaves as a strongly coupled theory[
Reference Fedotov, Ilderton, Karbstein, King, Seipt, Taya and Torgrimsson5,
Reference Fedotov86]. It is essential that large
$\alpha$
, are implied by the conjecture to become larger and larger as the order increases. The technical implication is that the perturbative expansion of QED breaks down and needs (somehow) to be re-summed[
Reference Heinzl, Ilderton and King85]; the physical implication is that QED enters a new ‘fully nonperturbative’ regime in which it behaves as a strongly coupled theory[
Reference Fedotov, Ilderton, Karbstein, King, Seipt, Taya and Torgrimsson5,
Reference Fedotov86]. It is essential that large
![]() $\chi$
is reached not by simply increasing the particle energy
$\chi$
is reached not by simply increasing the particle energy
![]() $\mathrm{\mathcal{E}}$
at low field strength, as the Ritus–Narozhny conjecture only applies in the high-intensity (locally constant, crossed field approximation (LCFA)) regime, where
$\mathrm{\mathcal{E}}$
at low field strength, as the Ritus–Narozhny conjecture only applies in the high-intensity (locally constant, crossed field approximation (LCFA)) regime, where
![]() ${a}^3/\chi \gg 1$
[
Reference Podszus and Di Piazza87,
Reference Ilderton88]. Furthermore, the mitigation of radiative energy losses requires the field duration to be kept as short as possible; for alternative scenarios see Refs. [Reference Baumann, Nerush, Pukhov and Kostyukov33, Reference Blackburn, Ilderton, Marklund and Ridgers89–Reference Tamburini and Meuren92].
${a}^3/\chi \gg 1$
[
Reference Podszus and Di Piazza87,
Reference Ilderton88]. Furthermore, the mitigation of radiative energy losses requires the field duration to be kept as short as possible; for alternative scenarios see Refs. [Reference Baumann, Nerush, Pukhov and Kostyukov33, Reference Blackburn, Ilderton, Marklund and Ridgers89–Reference Tamburini and Meuren92].
Nonlinear quantum dynamics are evident for pure EM fields as well, driven by virtual electron loops that modify the classical linearity of Maxwell’s equations. The nonlinear behaviour of pure magnetic field of strength,
![]() $B$
, is controlled by the Heisenberg–Euler interaction Lagrangian (see, e.g., Ref. [Reference Fedotov, Ilderton, Karbstein, King, Seipt, Taya and Torgrimsson5]). At the one-loop order,
$B$
, is controlled by the Heisenberg–Euler interaction Lagrangian (see, e.g., Ref. [Reference Fedotov, Ilderton, Karbstein, King, Seipt, Taya and Torgrimsson5]). At the one-loop order,
![]() $\mathrm{\mathcal{L}}={m}^4{\left(B/{B}_{\mathrm{cr}}\right)}^4/\left(360{\pi}^2\right)$
for
$\mathrm{\mathcal{L}}={m}^4{\left(B/{B}_{\mathrm{cr}}\right)}^4/\left(360{\pi}^2\right)$
for
![]() $B\ll {B}_{\mathrm{cr}}$
and
$B\ll {B}_{\mathrm{cr}}$
and
![]() $\mathrm{\mathcal{L}}={m}^4{\left(B/{B}_{\mathrm{cr}}\right)}^2\ln \left(B/{B}_{\mathrm{cr}}\right)/\left(24{\pi}^2\right)$
for
$\mathrm{\mathcal{L}}={m}^4{\left(B/{B}_{\mathrm{cr}}\right)}^2\ln \left(B/{B}_{\mathrm{cr}}\right)/\left(24{\pi}^2\right)$
for
![]() $B\gg {B}_{\mathrm{cr}}$
. For supercritical magnetic fields, higher-order corrections grow logarithmically, with the following[
Reference Karbstein93]:
$B\gg {B}_{\mathrm{cr}}$
. For supercritical magnetic fields, higher-order corrections grow logarithmically, with the following[
Reference Karbstein93]:
 $$\begin{align}\frac{{\mathrm{\mathcal{L}}}^{n-\mathrm{loop}}}{{\mathrm{\mathcal{L}}}^{1-\mathrm{loop}}}\sim {\left[\frac{\alpha }{\pi}\ln \left(\frac{B}{B_{\mathrm{cr}}}\right)\right]}^{n-1}.\end{align}$$
$$\begin{align}\frac{{\mathrm{\mathcal{L}}}^{n-\mathrm{loop}}}{{\mathrm{\mathcal{L}}}^{1-\mathrm{loop}}}\sim {\left[\frac{\alpha }{\pi}\ln \left(\frac{B}{B_{\mathrm{cr}}}\right)\right]}^{n-1}.\end{align}$$
Although this growth is slower than the power-law behaviour of higher-order corrections at ultralarge quantum parameter
![]() $\chi$
, as predicted (above) in the Ritus–Narozhny conjecture, re-summation is still required. Investigating this nonperturbative, nonlinear regime of electrodynamics motivates the creation of ultrastrong EM fields that are not probed by ultrarelativistic external particles.
$\chi$
, as predicted (above) in the Ritus–Narozhny conjecture, re-summation is still required. Investigating this nonperturbative, nonlinear regime of electrodynamics motivates the creation of ultrastrong EM fields that are not probed by ultrarelativistic external particles.
4 Summary
We have outlined how optimal configurations of laser systems and/or secondary sources could give us the opportunity to approach, or even exceed, the critical field of QED. The configurations presented certainly constitute immense engineering challenges. Realising an optical-XUV plasma converter demands sophisticated material engineering, high laser contrast and spatial uniformity, as well as timing and pointing stability. The quality of the vacuum is important if observations are to be made of Schwinger pair creation, or of the nuclear physics processes we have considered. These feasibility questions should be addressed in future work. Our results nevertheless indicate that the presented concepts are promising and warrant further analysis. Reaching such critical fields could give an opportunity to probe some of the most extreme environments in the universe, and investigate the behaviour of electrons, nuclei and the quantum vacuum under such conditions. We have given several examples of the use of such new photon sources for probing physical laws, ranging from electron and nuclear physics to probing the quantum vacuum.
Appendix A: Invariants
Consider the interaction of an electron with Lorentz factor
![]() ${\gamma}_0$
and a dipole wave that has maximum normalised field strength
${\gamma}_0$
and a dipole wave that has maximum normalised field strength
![]() $\varepsilon \equiv {E}_0/{E}_{\mathrm{cr}}$
and frequency
$\varepsilon \equiv {E}_0/{E}_{\mathrm{cr}}$
and frequency
![]() $\omega$
. The three most important invariants are as follows: the quantum nonlinearity parameter
$\omega$
. The three most important invariants are as follows: the quantum nonlinearity parameter
![]() $\chi ={\gamma}_0\varepsilon$
; the classical nonlinearity parameter
$\chi ={\gamma}_0\varepsilon$
; the classical nonlinearity parameter
![]() ${a}_0\,{=}\,\varepsilon m/\omega$
; and the field strength
${a}_0\,{=}\,\varepsilon m/\omega$
; and the field strength
![]() $f={\varepsilon}^2$
. In terms of the electron energy
$f={\varepsilon}^2$
. In terms of the electron energy
![]() ${\mathrm{\mathcal{E}}}_0$
, the input power
${\mathrm{\mathcal{E}}}_0$
, the input power
![]() $\mathcal{P}$
and wavelength
$\mathcal{P}$
and wavelength
![]() $\lambda =2\pi /\omega$
, these are as follows:
$\lambda =2\pi /\omega$
, these are as follows:
 $$\begin{align}\chi &=3.7\frac{{\mathrm{\mathcal{E}}}_0\kern0.1em \left[\mathrm{GeV}\right]{\mathcal{P}}^{1/2}\kern0.1em \left[\mathrm{PW}\right]}{\lambda \kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]},\quad {a}_0=780{\mathcal{P}}^{1/2}\kern0.1em \left[\mathrm{PW}\right],\nonumber\\ f&=3.6\times {10}^{-6}\frac{\mathcal{P}\kern0.1em \left[\mathrm{PW}\right]}{\lambda^2\kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]}.\end{align}$$
$$\begin{align}\chi &=3.7\frac{{\mathrm{\mathcal{E}}}_0\kern0.1em \left[\mathrm{GeV}\right]{\mathcal{P}}^{1/2}\kern0.1em \left[\mathrm{PW}\right]}{\lambda \kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]},\quad {a}_0=780{\mathcal{P}}^{1/2}\kern0.1em \left[\mathrm{PW}\right],\nonumber\\ f&=3.6\times {10}^{-6}\frac{\mathcal{P}\kern0.1em \left[\mathrm{PW}\right]}{\lambda^2\kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]}.\end{align}$$
Besides these three, we have the following:
 $$\begin{align}{\alpha \chi}^{2/3}&=0.017\frac{{\mathrm{\mathcal{E}}}_0^{2/3}\kern0.1em \left[\mathrm{GeV}\right]{\mathcal{P}}^{1/3}\kern0.1em \left[\mathrm{PW}\right]}{\lambda^{2/3}\kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]},\\ \frac{\chi }{a_0^3}&=7.8\times {10}^{-9}\frac{{\mathrm{\mathcal{E}}}_0\kern0.1em \left[\mathrm{GeV}\right]}{\mathcal{P}\kern0.1em \left[\mathrm{PW}\right]\lambda \kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]},\nonumber\\ \frac{f}{\chi^3}&=7.0\times {10}^{-8}\frac{\lambda \kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]}{{\mathrm{\mathcal{E}}}_0^3\kern0.1em \left[\mathrm{GeV}\right]{\mathcal{P}}^{1/2}\kern0.1em \left[\mathrm{PW}\right]}.\nonumber\end{align}$$
$$\begin{align}{\alpha \chi}^{2/3}&=0.017\frac{{\mathrm{\mathcal{E}}}_0^{2/3}\kern0.1em \left[\mathrm{GeV}\right]{\mathcal{P}}^{1/3}\kern0.1em \left[\mathrm{PW}\right]}{\lambda^{2/3}\kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]},\\ \frac{\chi }{a_0^3}&=7.8\times {10}^{-9}\frac{{\mathrm{\mathcal{E}}}_0\kern0.1em \left[\mathrm{GeV}\right]}{\mathcal{P}\kern0.1em \left[\mathrm{PW}\right]\lambda \kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]},\nonumber\\ \frac{f}{\chi^3}&=7.0\times {10}^{-8}\frac{\lambda \kern0.1em \left[\unicode{x3bc} \mathrm{m}\right]}{{\mathrm{\mathcal{E}}}_0^3\kern0.1em \left[\mathrm{GeV}\right]{\mathcal{P}}^{1/2}\kern0.1em \left[\mathrm{PW}\right]}.\nonumber\end{align}$$
These determine the importance of radiative corrections, non-local effects and background-field-driven processes (e.g., Schwinger pair creation[
Reference Gonoskov, Gonoskov, Harvey, Ilderton, Kim, Marklund, Mourou and Sergeev32]), respectively. They are plotted along with
![]() $\chi$
and
$\chi$
and
![]() ${a}_0$
in Figure 4 for an electron with
${a}_0$
in Figure 4 for an electron with
![]() ${\gamma}_0=2\times {10}^4$
. The LCFA, a standard assumption in simulation codes, requires both
${\gamma}_0=2\times {10}^4$
. The LCFA, a standard assumption in simulation codes, requires both
![]() $\chi /{a}_0^3\ll 1$
and
$\chi /{a}_0^3\ll 1$
and
![]() $f/{\chi}^3\ll 1$
.
$f/{\chi}^3\ll 1$
.

Figure 4 The invariants that characterise the interaction between an ultrarelativistic electron (
![]() ${\gamma}_0=2\times {10}^4$
) and a dipole wave generated by
${\gamma}_0=2\times {10}^4$
) and a dipole wave generated by
![]() $4\pi$
-focusing of a given input power at
$4\pi$
-focusing of a given input power at
![]() $\lambda =0.8\kern0.22em \unicode{x3bc} \mathrm{m}$
(red) and the third and tenth harmonics (orange, purple).
$\lambda =0.8\kern0.22em \unicode{x3bc} \mathrm{m}$
(red) and the third and tenth harmonics (orange, purple).
Appendix B: Pair cascades
For sufficiently strong laser fields it becomes possible to generate electron–positron pairs through the Schwinger mechanism. Even in a perfect vacuum, this opens up the possibility for the creation of seed particles that can in turn trigger an avalanche-type pair production cascade through the nonlinear Breit–Wheeler process. However, since these two processes work over different time and length scales, it may be possible to produce a large number of electron–positron pairs through the Schwinger mechanism, without necessarily triggering an avalanche cascade.
The number of electron–positron pairs that can be produced through the Schwinger mechanism is given by the following:
 $$\begin{align}N_{\mathrm{p}}^\mathrm{Schwinger} = \frac{1}{4\pi^3 \lambda_{\mathrm{C}}^4} \int {\mathrm{d}}x^4 \mathscr{E}^2 \exp({-\pi/\mathscr{E}}),\end{align}$$
$$\begin{align}N_{\mathrm{p}}^\mathrm{Schwinger} = \frac{1}{4\pi^3 \lambda_{\mathrm{C}}^4} \int {\mathrm{d}}x^4 \mathscr{E}^2 \exp({-\pi/\mathscr{E}}),\end{align}$$
where
![]() $\mathrm{\mathcal{E}}=\sqrt{\mid \mathcal{S}\mid +\mathcal{S}}/{E}_{\mathrm{cr}}$
, with
$\mathrm{\mathcal{E}}=\sqrt{\mid \mathcal{S}\mid +\mathcal{S}}/{E}_{\mathrm{cr}}$
, with
![]() $\mathcal{S}=\frac{1}{2}\left({\mathbf{E}}^2-{c}^2{\mathbf{B}}^2\right)$
and assuming that
$\mathcal{S}=\frac{1}{2}\left({\mathbf{E}}^2-{c}^2{\mathbf{B}}^2\right)$
and assuming that
![]() $\mathbf{E}\cdot c\mathbf{B}=0$
. Here it is also assumed that the characteristic scale of Schwinger pair production is much smaller than the characteristic scale of the EM field, such that the total number of pairs can be obtained by integrating the local pair production rate over the 4-volume[
Reference Bulanov, Narozhny, Mur and Popov29].
$\mathbf{E}\cdot c\mathbf{B}=0$
. Here it is also assumed that the characteristic scale of Schwinger pair production is much smaller than the characteristic scale of the EM field, such that the total number of pairs can be obtained by integrating the local pair production rate over the 4-volume[
Reference Bulanov, Narozhny, Mur and Popov29].
As can be seen in Equation (B1), the pair production is strongly dependent on the field strength. In Table 2 we present the estimated peak field values of four different field configurations: (1) an
![]() $f/1$
-focused optical field; (2) a
$f/1$
-focused optical field; (2) a
![]() $4\pi$
-focused optical field; (3) an
$4\pi$
-focused optical field; (3) an
![]() $f/1$
-focused XUV field; and (4) a dipole-focused XUV field using
$f/1$
-focused XUV field; and (4) a dipole-focused XUV field using
![]() $6\times f/1$
as described in Section 2.3. We have here assumed an optical wavelength of
$6\times f/1$
as described in Section 2.3. We have here assumed an optical wavelength of
![]() $0.8\kern0.22em \unicode{x3bc} \mathrm{m}$
and that the plasma conversion is performed at
$0.8\kern0.22em \unicode{x3bc} \mathrm{m}$
and that the plasma conversion is performed at
![]() ${10}^{22}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
for the XUV fields. We also present the maximum attainable
${10}^{22}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
for the XUV fields. We also present the maximum attainable
![]() $\chi$
for a
$\chi$
for a
![]() $10\kern0.22em \mathrm{GeV}$
electron interacting with the peak field. For a plasma conversion at
$10\kern0.22em \mathrm{GeV}$
electron interacting with the peak field. For a plasma conversion at
![]() ${10}^{23}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
the peak fields, as well as the maximum
${10}^{23}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
the peak fields, as well as the maximum
![]() $\chi$
, will be increased by a factor of
$\chi$
, will be increased by a factor of
![]() $13/\sqrt{10}\approx 4.1$
. Because the minimum power required to reach an intensity of
$13/\sqrt{10}\approx 4.1$
. Because the minimum power required to reach an intensity of
![]() ${10}^{22}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
(
${10}^{22}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
(
![]() ${10}^{23}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
) at the plasma converter is
${10}^{23}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
) at the plasma converter is
![]() ${\mathcal{P}}^{\mathrm{min}}=0.087\kern0.1em \mathrm{PW}$
(0.87 PW), assuming
${\mathcal{P}}^{\mathrm{min}}=0.087\kern0.1em \mathrm{PW}$
(0.87 PW), assuming
![]() $f/1$
focusing, we restrict ourselves to laser powers above 1 PW.
$f/1$
focusing, we restrict ourselves to laser powers above 1 PW.
Table 2 The table shows, for each power and field configuration, the following: (1) the peak field strength
![]() ${E}_0/{E}_{\mathrm{cr}}$
; and (2) the maximum attainable
${E}_0/{E}_{\mathrm{cr}}$
; and (2) the maximum attainable
![]() ${\chi}_0={\gamma}_0{E}_0/{E}_{\mathrm{cr}}$
for a
${\chi}_0={\gamma}_0{E}_0/{E}_{\mathrm{cr}}$
for a
![]() $10\kern0.22em \mathrm{GeV}$
electron interacting with the peak field. Values where
$10\kern0.22em \mathrm{GeV}$
electron interacting with the peak field. Values where
![]() ${\alpha \chi}_0^{2/3}>1$
are presented in bold.
${\alpha \chi}_0^{2/3}>1$
are presented in bold.

In Table 3 we present an estimate for the Schwinger pair production by applying Equation (B1) to both an optical dipole wave and to a dipole-focused XUV field, as described by Equation (7). The estimates are presented as the number of pairs per optical cycle, disregarding any potential secondary effects due to the produced pairs. To evaluate if pair plasma effects may nevertheless come into play, we further estimate the density of the produced pairs and compare it to the plasma critical density,
![]() ${n}_{\mathrm{c}\mathrm{r}}=\sqrt{1+{a}_0^2}{n}_{\mathrm{c}}$
. We obtain the density estimate by assuming that all pairs produced will be distributed within a volume
${n}_{\mathrm{c}\mathrm{r}}=\sqrt{1+{a}_0^2}{n}_{\mathrm{c}}$
. We obtain the density estimate by assuming that all pairs produced will be distributed within a volume
![]() $\mathcal{V}$
, taken as the volume where the field strength is
$\mathcal{V}$
, taken as the volume where the field strength is
![]() $E/{E}_0>1/2$
. For the optical dipole, the plasma critical density is
$E/{E}_0>1/2$
. For the optical dipole, the plasma critical density is
![]() ${n}_{\mathrm{c}}=1.7\times {10}^{21}\kern0.1em {\mathrm{c}\mathrm{m}}^{-3}$
and the characteristic field volume is
${n}_{\mathrm{c}}=1.7\times {10}^{21}\kern0.1em {\mathrm{c}\mathrm{m}}^{-3}$
and the characteristic field volume is
![]() $\mathcal{V}=4.9\times {10}^{-14}\kern0.1em {\mathrm{cm}}^3$
. For the dipole-focused XUV field, the plasma critical density is
$\mathcal{V}=4.9\times {10}^{-14}\kern0.1em {\mathrm{cm}}^3$
. For the dipole-focused XUV field, the plasma critical density is
![]() ${{n}_{\mathrm{c}}=1.1\times {10}^{27}\kern0.1em {\mathrm{c}\mathrm{m}}^{-3}}$
and the characteristic field volume is
${{n}_{\mathrm{c}}=1.1\times {10}^{27}\kern0.1em {\mathrm{c}\mathrm{m}}^{-3}}$
and the characteristic field volume is
![]() $\mathcal{V}=5.2\times {10}^{-22}\kern0.1em {\mathrm{cm}}^3$
, where plasma conversion at
$\mathcal{V}=5.2\times {10}^{-22}\kern0.1em {\mathrm{cm}}^3$
, where plasma conversion at
![]() ${10}^{22}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
has been assumed and where the wavelength has been taken as the characteristic size of the field (
${10}^{22}\kern0.1em \mathrm{W}/ {\mathrm{cm}}^2$
has been assumed and where the wavelength has been taken as the characteristic size of the field (
![]() $2R$
), as defined in Equation (7).
$2R$
), as defined in Equation (7).
Table 3 The table shows, for different values of
![]() $\mathcal{P}$
and for two different field configurations, the following: (1) the peak field strength,
$\mathcal{P}$
and for two different field configurations, the following: (1) the peak field strength,
![]() ${E}_0/{E}_{\mathrm{cr}}$
; (2) the estimated number of pairs produced per optical cycle through the Schwinger mechanism,
${E}_0/{E}_{\mathrm{cr}}$
; (2) the estimated number of pairs produced per optical cycle through the Schwinger mechanism,
![]() ${N}_{\mathrm{p}}^{\mathrm{Schwinger}}$
; (3) the estimated pair plasma density normalised to the critical density,
${N}_{\mathrm{p}}^{\mathrm{Schwinger}}$
; (3) the estimated pair plasma density normalised to the critical density,
![]() ${N}_{\mathrm{p}}^{\mathrm{Schwinger}}/\mathcal{V}{n}_{\mathrm{cr}}$
; and (4) the particle growth rate due to Breit–Wheeler pair creation,
${N}_{\mathrm{p}}^{\mathrm{Schwinger}}/\mathcal{V}{n}_{\mathrm{cr}}$
; and (4) the particle growth rate due to Breit–Wheeler pair creation,
![]() $\Gamma T$
. These results represent an upper limit on the pair creation yield, assuming the field is an electric dipole wave.
$\Gamma T$
. These results represent an upper limit on the pair creation yield, assuming the field is an electric dipole wave.

Finally, we also present estimates for the multiplication factor due to Breit–Wheeler pair production, over a single optical cycle. For the optical dipole the growth rate is given by
![]() $\Gamma \left(\mathcal{P}\right)\approx 3.21{T}^{-1}\left({\mathcal{P}}^{1/3}-{\mathcal{P}}_{\mathrm{min}}^{1/3}\right)$
, where
$\Gamma \left(\mathcal{P}\right)\approx 3.21{T}^{-1}\left({\mathcal{P}}^{1/3}-{\mathcal{P}}_{\mathrm{min}}^{1/3}\right)$
, where
![]() ${\mathcal{P}}_{\mathrm{min}}=7.2\kern0.22em \mathrm{PW}$
and
${\mathcal{P}}_{\mathrm{min}}=7.2\kern0.22em \mathrm{PW}$
and
![]() $T$
is the optical period[
Reference Gonoskov, Bashinov, Bastrakov, Efimenko, Ilderton, Kim, Marklund, Meyerov, Muraviev and Sergeev14]. For the dipole-focused XUV field we instead estimate an upper bound for the multiplication factor. This is done by computing the growth factor due to Breit–Wheeler pair production for a seed particle in a constant field of strength
$T$
is the optical period[
Reference Gonoskov, Bashinov, Bastrakov, Efimenko, Ilderton, Kim, Marklund, Meyerov, Muraviev and Sergeev14]. For the dipole-focused XUV field we instead estimate an upper bound for the multiplication factor. This is done by computing the growth factor due to Breit–Wheeler pair production for a seed particle in a constant field of strength
![]() ${E}_0/{E}_{\mathrm{cr}}$
(even though we are aware that a tree-level calculation of the Breit–Wheeler rate will not be valid for very high
${E}_0/{E}_{\mathrm{cr}}$
(even though we are aware that a tree-level calculation of the Breit–Wheeler rate will not be valid for very high
![]() $\chi$
), and assuming that all generated particles are produced with the same constant
$\chi$
), and assuming that all generated particles are produced with the same constant
![]() ${\chi}_0={\gamma}_0{E}_0/{E}_{\mathrm{cr}}$
as the parent particle. The growth factor is taken as the number of particles after a time
${\chi}_0={\gamma}_0{E}_0/{E}_{\mathrm{cr}}$
as the parent particle. The growth factor is taken as the number of particles after a time
![]() $R/c$
, corresponding to the typical time it would take a seed particle to escape the field.
$R/c$
, corresponding to the typical time it would take a seed particle to escape the field.
Table 3 shows that the number of pairs produced through the Schwinger mechanism is greatly increased for the dipole-focused XUV field, due to the increased field strength. At the same time, the cascade growth rate (due to Compton scattering and Breit–Wheeler pair production) is likely reduced over a single cycle. Over multiple cycles, the XUV field is even less likely to maintain a cascade, as the field now constitutes an individual burst with no means of continuous particle trapping between cycles. The table further suggests that the number of Schwinger pairs produced would surpass the plasma critical density, if entirely contained within the strong-field region, which might hinder the field strength from reaching its theoretical maximum. Whether a field strength greater than
![]() ${E}_{\mathrm{cr}}$
would always, if at all, generate such a dense pair plasma through the Schwinger mechanism would require more detailed analysis accounting for the particle dynamics, which lies outside the scope of this paper.
${E}_{\mathrm{cr}}$
would always, if at all, generate such a dense pair plasma through the Schwinger mechanism would require more detailed analysis accounting for the particle dynamics, which lies outside the scope of this paper.
Acknowledgements
This research was supported by the Swedish Research Council Grants Nos. 2016-03329 and 2020-06768 (T.G.B. and M.M.), and 2017-05148 (A.G.), as well as the U.S. Department of Energy Office of Science Offices of High Energy Physics and Fusion Energy Sciences (through LaserNetUS), under Contract No. DE-AC02-05CH11231 (S.S.B.). Simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC).