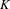Performance of an elliptical crystal spectrometer for SGII X-ray opacity experiments

Abstract

A new crystal spectrometer for application in X-ray opacity experiments is proposed. The conditions necessary to yield broad spectral coverage with a resolution ${>}$500, strong rejection of hard X-ray backgrounds and negligible source broadening for extended sources are formulated. In addition, the design, response modeling and reporting of an elliptical crystal spectrometer in conjunction with a linear detector are presented. The measured results demonstrate the performance of the new crystal spectrometer with a broad energy coverage range, high spectral resolution, and high luminosity (good collection efficiency). This spectrometer can be used in combination with point-projection backlighting techniques as utilized in X-ray opacity experiments. Specifically, the X-ray source, transmission and self-emission spectra of the sample can be measured simultaneously in a single shot, which can reduce the experimental uncertainties from shot-to-shot fluctuations. The new crystal spectrometer has been used in the X-ray opacity experiment to precisely measure the aluminum $K$-absorption edge shift in the energy range around 1.560 keV in strongly compressed matter. It is demonstrated that the spectrometer can be used to realize measurements of new and unpredictable physical interactions of interest, as well as basic and applied high-energy-density science.

1 Introduction

Opacity is important for terrestrial plasmas for inertially and magnetically confined fusion programs. The theoretical and experimental study of the X-ray absorption characteristics of these plasmas is an active field of research with applications in inertial confinement fusion (ICF) and X-ray laser production^[1–5]. As a result, accurate X-ray absorption spectroscopy data are essential to validate theoretical models and plasma diagnostics over a broad range of temperatures and densities. Among these studies, much effort has been devoted to improving the experimental accuracy^{[6, 7]}. The development of this spectrometer allows high spectral, spatial and temporal resolution measurements to be made to study line profiles in detail. Knapp et al. ^[8] had used the spherically bent crystal spectrometer to measure the absorption spectra with high spectral resolution, but in X-ray opacity experiments, instruments with broad X-ray energy coverage are particularly important. Specifically, the absorption of the plasma should be measured over a broad spectral range relevant to radiation transport, and the spectral resolution of the instrument should be sufficiently high to distinguish typical features of the underlying physics. Especially, one of the dominant trends in X-ray opacity measurements today is the measurement of the self-emission spectrum, backlighting source spectrum and transmitted spectrum in a single shot. In addition, to compare with theoretical models, the temperature and density of the plasma must be measured concurrently with the absorption and self-emission spectra^{[9, 10]}. Moreover, for an accurate opacity measurement, the precision of the relative intensity calibration and a spectral resolution $E/\unicode[STIX]{x0394}E>500$ throughout their spectral range are desirable.

The new crystal spectrometer described here uses an elliptically bent crystal based on focusing geometry^{[11, 12]}. In preparation for this type of X-ray spectrograph development, we recently completed several basic studies achieving the simultaneous measurement of plasma diagnostics and the appropriate spectral information. In an elliptical geometry, the crossover point of the given elliptical geometry is fixed for all Bragg reflection angles and is real rather than virtual at the focal point. Extended sources are de-magnified along the dispersive axis. Because of this, the elliptical design offers higher spectral resolutions compared to flat crystals^[13] and thus achieves a greater spectral range compared to convex cylindrical designs^[14]. With the elliptically bent crystal, an effective scatter aperture can be located at this crossover position. The low-energy background radiation that may be superimposed on the higher-energy measured spectra can be excessive. To suppress this low-energy background, a relatively thick filter with a strong transmission band for the particular spectral region being measured can often be effective (usually placed at the small scatter aperture). A major obstacle to achieving the design goals arises from the problem of producing a high spectral resolution, high luminosity, time-resolved spectra or time-integrated spectra spanning a large photon energy range. This spectrometer will provide more accurate temperature and density information compared to traditional crystal spectrometer in the X-ray opacity experiments^[15], detailed spectra of ICF plasmas and other high-energy-density (HED) physics experimental applications at the ShenguangII (SGII) laser facility.

This paper is organized as follows. In Section 2, we describe the general design of the elliptically bent crystal spectrometer. The results of the testing and operation of the crystal spectrometer are presented in Section 3, while Section 4 presents the absorption spectra obtained with the spectrometer. Finally, Section 5 summarizes the results of the work.

2 Elliptical crystal spectrometer performance

Crystals exhibit a property in which a single monochromatic ray is only reflected at a particular angle (or, more correctly, a narrow cone of angles). All crystal spectrometers are based on Bragg’s law:

(1) $$\begin{eqnarray}\displaystyle 2d\sin \unicode[STIX]{x1D703}=\unicode[STIX]{x1D706}, & & \displaystyle\end{eqnarray}$$

where $d$ is the spacing between the reflecting planes of the crystal and $\unicode[STIX]{x1D703}$ is the Bragg angle, which is the angle of the ray with respect to a particular set of diffracting planes. Opacity experiments are typically designed to measure spectrally resolved transmission using a spectrometer that views the backlighter spectra through the sample. As the spectrometer characteristics most important for the present opacity measurements include the spectral coverage range, spectral resolving power and efficiency output signal (and signal/noise ratio), we now discuss the aspects of these characteristics of the crystal spectrograph and their application to X-ray opacity experiments. In Figure 1, a schematic of the elliptically bent crystal spectrometer is shown. The ellipse parameters and location of the detector were optimized by maximizing the spectrum to span a large photon energy range and high spectral resolution within the physical constraints of the system. These constraints include the diagnostic space envelope on the laser target chamber of the SGII laser facility and the minimum radius of curvature to which the crystals can be bent. The parameters that define the spectrometer geometry are the ellipse eccentricity $\unicode[STIX]{x1D700}$ , focal length $2f$ and inclination angle $\unicode[STIX]{x1D702}$ of the semi-major axis with respect to the source–diagnostic port centerline. A ray-tracing code was developed and used to determine the optimized parameters at the ( $\unicode[STIX]{x1D700}$ , $2f$ , $\unicode[STIX]{x1D702}$ ) configuration space. The final optimized parameters are $\unicode[STIX]{x1D700}=0.9677$ , $2f=600~\text{mm}$ and $\unicode[STIX]{x1D702}=1.8759^{\circ }$ . In Figure 1, the crystal is bent along the surface of the ellipse but remains flat in the direction perpendicular to the plane of the ellipse. The detector is placed beyond the crossover point at the second focus and can thus be adjusted to any practical size. A range of Bragg angles from $22^{\circ }$ to $78^{\circ }$ was chosen to meet the spectral range requirements. The spectral coverage of the diagnostic instrument is roughly 1.49–7.78 keV, which was achieved using three different lattice spacings of an elliptically bent crystal: quartz with $2d$ lattice spacings of 8.512, 6.687 and 4.246 Å. Its main characteristics are shown in Table 1 and have been chosen in order to be able to cover the spectral range with a single crystal and to have a compact instrument. The 90 mm length of the crystal is the maximum length for a good quality curved crystal.

Figure 1. Schematic of the locations of the elliptical crystal segment and detector surface relative to the X-ray source and diagnostic space. The optimized parameters are $\unicode[STIX]{x1D700}=0.9677$ , $2f=600$  mm and $\unicode[STIX]{x1D702}=1.8759^{\circ }$ . $\unicode[STIX]{x1D712}$ is measured from the ellipse semi-major axis to the initial X-ray trace, $\unicode[STIX]{x1D703}$ is the Bragg angle, and $\unicode[STIX]{x1D6FD}$ is the angle of the X-ray through the crossover focus.

Table 1. Main characteristics of the described spectrometer.

The spectral resolution of the elliptically bent crystal spectrometer has contributions from the source broadening, crystal resolution and detector resolution. Given here are the $2d$ values, photon energy limits for Bragg angles from $22^{\circ }$ to $78^{\circ }$ and estimated spectral resolution for a Bragg angle of $45^{\circ }$ . The spectral resolving power of the instrument is obtained by summing the squares of the resolving powers because of the following three contributions.

(a) The crystal intrinsic spectral resolution $S_{\text{c}}$ , essentially determined by the imperfection of the lattice $(\unicode[STIX]{x1D706}/\unicode[STIX]{x0394}\unicode[STIX]{x1D706})_{\text{int}}$ , is about 1000 for an $\unicode[STIX]{x1D6FC}$ -quartz $\text{SiO}_{2}$ (20–20, $2d=4.246$  Å) flat crystal. In a bent crystal, some atomic bonds break because of the stretching/compression of the lattice. Strong gradients of internal strain are present, especially on the edges. This typically degrades the resolution and focalization as much as the radius of curvature is reduced. The resolution can consequently be smaller than 1000.

(b) The resolution due to the detector $S_{\text{d}}$ : the imaging plate (IP) as a detector produces images with a pixel size 25  $\unicode[STIX]{x03BC}$ m, the inclination angle $\unicode[STIX]{x1D702}$ of the semi-major axis with respect to the source–diagnostic port centerline is $1.8759^{\circ }$ , and the resolution is $S_{\text{d}}=\unicode[STIX]{x1D706}/\unicode[STIX]{x0394}\unicode[STIX]{x1D706}\approx 2073$ , which is much bigger than  $S_{\text{c}}$ .

(c) The resolution of the source $S_{\text{s}}$ due to the tangential curvature of the crystal: it is easy to find a configuration where $S_{\text{s}}$ is bigger than $S_{\text{c}}$ and $S_{\text{d}}$ ^[10] based on the negligible effect on the source size. In our working configuration (with $2f=600$  mm, $\unicode[STIX]{x1D700}=0.9677$ , $\unicode[STIX]{x1D6FD}=45^{\circ }$ and the slit width $\unicode[STIX]{x1D6FF}=4$  mm), $S_{\text{s}}\approx 4300$ . This is a satisfactory value for our purpose.

Hence, the limiting resolution is determined predominantly by the intrinsic spectral resolution of the crystal. The predicted resolving power of the instrument is $\unicode[STIX]{x1D706}/\unicode[STIX]{x0394}\unicode[STIX]{x1D706}\geqslant 900$ over the full spectral range.

In addition, another critical characteristic of spectrometer performance is the collection efficiency. The detector is calibrated in terms of the energy per unit surface area. We would thus like to relate the exposure back to the total flux radiated by the source (assuming isotropic radiation). For elliptical designs, the geometry of the spectrographic system plays an important role in the instrument response. Following Ref. [14], it is defined for three angles that characterize this geometry, as shown in Figure 1. Here, $\unicode[STIX]{x1D712}$ is the angle from a point source to a given differential element of the ellipse measured from the semi-major axis, and $\unicode[STIX]{x1D6FD}$ is the measured angle. These angles follow the relation

(2) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}=2\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6FD}. & & \displaystyle\end{eqnarray}$$

Thus, let us now analyze the behavior of this system for broadband spectroscopy measurements. In this geometry, X-rays emerging from a source at one focus of the ellipse are Bragg-reflected off the crystal, passes through the second focus of the ellipse and is then recorded by a detector. For the number of photons per second per unit area at the detector, we define two length parameters: $r$ , the distance from the crossover focus of the ellipse to the detector, and $L$ , the distance from the source to the ellipse element added to the distance from the ellipse to the detector. The absolute source brightness for a characteristic line emission at photon energy $E$ may be assumed as $S$ photons/(sr $\cdot$ s $\cdot$ eV), and the number of photons, $\text{d}N$ , per unit area per second at the circular arc detector can be given by the following relation [see Ref. [14], Equation (3)]:

(3) $$\begin{eqnarray}\displaystyle \frac{\text{d}N}{\text{d}A}=\left(\frac{S}{rL}\right)\left(\frac{\text{d}\unicode[STIX]{x1D712}}{\text{d}\unicode[STIX]{x1D703}}\right)\left(\frac{\text{d}\unicode[STIX]{x1D703}}{\text{d}\unicode[STIX]{x1D6FD}}\right)\left(\frac{\text{d}E}{\text{d}\unicode[STIX]{x1D703}}\right)R=SF_{g}R, & & \displaystyle\end{eqnarray}$$

where the factor $F_{g}$ depends only on the geometry of the spectrometer system, $\text{d}A$ is the differential area of the diffracted beam at the detector and $R$ (rad) is the integrated reflectivity of the crystal. Section 3 outlines design optimizations and laboratory demonstrations that seek to anticipate the emerging diagnostic needs related to the registering of the spectra from both the high-intensity and high-energy X-ray source. We have anticipated that the optimum working range for the measured angle $\unicode[STIX]{x1D6FD}$ is about $45^{\circ }$ to $155^{\circ }$ (e.g., to maximize dispersion and minimize background by avoiding smaller angles, and to satisfy typical spectrographic mechanical constraints for larger-angle diffractions). It is straightforward to obtain the dispersion relations for a linear detection arrays. The factor $F_{g}$ is plotted using a flat detector surface instead of a circular arc in Figure 2 for the design parameters of this spectrometer. As shown in the figure, the geometry factor has a significant effect on the decrease in photon intensity from high to low energy at the detector position. This effect is mitigated partially by the detector response versus energy and, in many cases, the spectrum of the source. The collection efficiency in the elliptically bent designed spectrometer has been modeled to help choose the filters for each crystal and to provide a calibration of the relative X-ray intensity of the measured data.

Figure 2. Geometry factor $Fg$ influencing the X-ray intensity reaching the linear detector versus detector position in the elliptically bent spectrometer design.

Figure 3. Example of IP-recorded Cl spectra using the quartz (10–10) ( $2d=8.512$  Å) crystal elliptical analyzer. (a) Raw spectral data recorded by IP. (b) Spectral intensity, obtained by averaging over the photon counts in the direction perpendicular to the dispersion direction of the detector, versus photon energy.

3 Experimental tests

The new crystal spectrometer was used at the SGII laser facility. The target was irradiated with up to four beams using a one-side irradiation scheme at an angular cone of $42^{\circ }$ from the target normal using a 1-ns temporally square profile at a wavelength of 0.527  $\unicode[STIX]{x03BC}$ m. The four beams were focused with $f/3$ focusing lenses with a spot size diameter of about 150  $\unicode[STIX]{x03BC}$ m. The average energy was about 500 J/beam. To test the broadband and spectral resolution, the target materials chosen herein were performed with aluminum, chlorine, titanium, copper, molybdenum and gold. For the Al $K$ radiation (1.49–3.89 keV), Cl L-shell radiation and Au $M$ -band spectra, a quartz (10–10) ( $2d=8.512$  Å) Bragg diffraction crystal was utilized. The Mo spectra were also acquired with a quartz (10–11) ( $2d=6.687$  Å) crystal, while the Ti and Cu spectra were produced using a quartz (20–20) ( $2d=4.246$  Å) diffracting element. Filters located at the crossover focus were required to block laser light and chosen to produce $K$ - and $L$ -shell absorption edges as a further wavelength scale calibration. The IP as the detector (BAS-SR2025) is from Fuji Film. The IP are digitized using a commercial reader (BAS-1800)^{[16, 17]}. Specific examples of the spectrometer that have been successfully applied in the experiments for a broad energy range are presented in the obtained spectral photograph. An indication of the resolving power of the spectrometer is given by line widths measured at the SGII laser facility. A typical spectrum obtained at the SGII laser facility is presented in Figure 3. Figure 3(a) displays the raw spectral data obtained with the new crystal spectrometer. As expected, the spectral features appear as straight lines on the detector. Figure 3(b) presents a lineout of the spectral data from Figure 3(a) and represents the spectral intensity profiles obtained by averaging over a band of pixels in the direction perpendicular to the dispersion direction of the IP. The observed full-width at half-maximum (FWHM) of the line labeled (1s $^{2}$ -1s3p) He-like alpha transition $\unicode[STIX]{x0394}E_{\text{FWHM}}$ is 3.087 eV and the corresponding energy $E$ is about 2.779565 keV. The measured resolving power of the new instrument $E/\unicode[STIX]{x0394}E_{\text{FWHM}}$ is about 900. This line is recorded near the center of the detector. Assuming a Gaussian instrument response function, the width of a measured line profile is given by

(4) $$\begin{eqnarray}\displaystyle & & \displaystyle \left(\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D706}}\right)_{\text{Measured}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left[\left(\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D706}}\right)_{\text{Doppler}}^{2}+\left(\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D706}}\right)_{\text{Instrument}}^{2}\right]^{1/2}.\end{eqnarray}$$

Note that Doppler and instrumental broadening are folded in. The analysis of the Doppler broadening effect is folded into the instrumental broadening profile, and its effect is very small, whereas the resolving power of the instrument at the center of the detector is approximately 900. Similarly, Figure 3 clearly demonstrates the high dispersion feature of the spectrometer.

4 Spectrometer applications

The study of the radiative properties of plasma requires simultaneous measurements of the temperature, density and absorption or emission spectrum. We now apply the developed instrument described above to the X-ray opacity experimental measurement. The aim of our experiment is to develop techniques that could provide more reasonable opacity data compared to traditional ones. This method is a point-projection spectroscopy technique in combination with a half sample sandwich target to measure the transmission of the shock-compressed material. Figure 4 shows a schematic of the experimental setup. The diagnostic aperture is placed between the sample target and spectrometer so that the sample emission, backlighter spectrum and transmission spectrum can be recorded independently on three different imaging zones of the same piece of IP. The X-ray backlight was first produced by a short, tightly focused laser beam on the backlight target, passed through the sample target, and spectrally dispersed by the elliptically bent crystal onto the IP. Point-projection backlighting spectrometry provides spectral and spatial information simultaneously, and provides temporal resolution, which is derived from the finite duration of the backlight^[18] obtained using flash radiography.

Figure 4. Schematic of the experimental setup for the point projection of the Al $K$ -edge absorption measurements.

The sample target, with a half sample sandwich target consisting of a 2- $\unicode[STIX]{x03BC}$ m-thick Al foil and approximately 15- $\unicode[STIX]{x03BC}$ m of plastic coated on both sides, and the other half consisting of the CH tamper, is symmetrically irradiated by four beams on one side and four beams on the other side at $\unicode[STIX]{x1D706}=0.351~\unicode[STIX]{x03BC}$ m with an incident irradiance of laser power intensity $I\approx 10^{14}~\text{W}/\text{cm}^{2}$ and pulse duration of about 2 ns. The focal spot has a diameter of about 300  $\unicode[STIX]{x03BC}$ m in the target plane, which determines the dimension of the shock-compressed region to be investigated. The shock waves propagated from both sides in the plastic layer and reached the Al foil. The consequent compression provides a density that is several times the solid density within the colliding shock region. As we know, colliding shocks produce higher compressions than single shocks for a given laser intensity. Each shock is reflected from the middle and propagates backward in the already compressed matter. A point source of X-rays is used to project a two-dimensional radiograph of the sample target onto the IP. In this case, we must produce a bright and uniform source with the laser-produced backlight plasma. Furthermore, a relatively smooth backlighter spectrum is required because the line structure may lead to transmission errors that are very difficult to account for. The problem remains to produce an intense X-ray source with smooth featureless spectra and calibrate the absorbed X-ray source, i.e., the backlighter. Ideally, the backlighter pulse would still have a very short duration so that the recorded spectrum, also retaining the full spatial information of the sample target, truly represents a snapshot of the sample conditions at some instant in time. Therefore, the brightness of the point source is formed from $M$ -shell emitters (e.g., Au) irradiated with a ninth laser beam. The laser energy was about 180 J and the pulse width was about 75 ps in the FWHM Gaussian profile. The ninth laser-driven beam was delayed by 400 ps with respect to the two opposing, four laser-compressed beams to obtain the maximum X-ray emission at the time of maximum compression of the half sample sandwich target. Figure 5 shows the backlighter spectrum detected by the spectrometer. The Au $M$ -band radiation spans from about 1.54 to 3.8 keV. We can see in this figure that the intensity of the backlight source is quasi-continuous across the desired spectral region. A spectral line structure is also observed, i.e., it is not a pure continuum. Note that the diagnostic technique employs a point X-ray-emitting plasma source generated from a picosecond laser to provide the required data in a single shot for opacity measurement. As a result, an analysis of the data was not necessary to obtain temporal variations of the sample condition.

Figure 5. Au $M$ -band spectrum from 1.54 to 3.8 keV.

The obtained measurements are listed as follows: (1) backgrounds from IP chemical fog and crystal X-ray fluorescence; (2) Al absorption using a sandwich target, shock-compressed region and backlighter to produce absorption spectra; (3) sample emission and (4) backlight source. As absolute calibration is difficult, it is preferable to have all the information recorded on the same piece of IP. The principle is illustrated in Figure 4, where a point-projection spectrometer is used to record the spectrum on a single piece of IP while the IP is scanned with a commercial reader (BAS-1800). The data were subsequently analyzed by converting the IP density to intensity using a calibrated step wedge. The first background to be subtracted was the IP chemical fog, and then the IP density was converted to the measured intensity, $I_{\text{m}}$ . Next, the backgrounds from the self-emission of the sample, $I_{\text{s}}$ , and fluorescence from inside the spectrometer, $I_{\text{f}}$ , were subtracted correspondingly. As shown in Figure 4, through the CH tamper, the backlighter X-rays passed unattenuated. By dividing the image by this photon-energy-dependent, unattenuated backlighter spectrum, $I_{b}$ , the transmission, $T(E)$ , of the samples can be obtained:

(5) $$\begin{eqnarray}\displaystyle T(E)=\text{e}^{-k(E)}=(I_{m}-I_{s}-I_{f})/(I_{b}-I_{s}-I_{f}), & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D705}(E)$ is the photon-energy-dependent absorption coefficient in $\text{cm}^{2}/\text{g}$ and $w$ is the path length in $\text{g}/\text{cm}^{2}$ through the sample. Figure 6 presents the spectra of the transmission, which show $K\unicode[STIX]{x1D6FC}$ absorption lines from H-like to He-like Al ions, and Al $K$ -shell X-ray resonance absorption. The Al $K$ absorption edge was calibrated to about 1.5567 keV, while the normal position of the Al $K$ -edge was at 1.560 keV^[19]. The edge then shifted back toward its normal position at 1.560 keV as the target decompressed. This red-shift feature of the $K$ -edge was highly reproducible.

Figure 6. Experimentally measured Al transmission data with the new crystal spectrometer.

5 Conclusions

A new crystal spectrometer for application in X-ray opacity experiments was developed and tested at the SGII laser facility. The high resolution, precision, and sensitivity of the instrument were discussed in detail and illustrated with typical examples of applications. Preliminary experimental results confirm that the spectral coverage range of the instrument ranges from roughly 1.49 to 7.78 keV, and the spectral resolution $(E/\unicode[STIX]{x0394}E)\sim 900$ . The observed and theoretically predicted photon energy dispersions on the detector are in agreement within experimental error. Utilizing the half sample sandwich target and point-projection method, the instrument enables us to measure the spectra of the self-emission, backlighter and absorption concurrently in a single shot. This can greatly reduce the experimental uncertainties from shot-to-shot fluctuation caused by the spot size, laser beam and target parameters. The Al $K\unicode[STIX]{x1D6FC}$ absorption lines were obtained with our new spectrometer for the laser-shock-compressed sample case. This spectrometer presents the main characteristics of broad spectral coverage, sensitivity, crystal planarity perpendicular to the dispersion direction, wavelength accuracy and spectral resolution, as well as the strong rejection of hard X-ray backgrounds, which is promising for X-ray opacity measurements.

In the future, the spectrometer may have many applications, including spectral fine structure measurement, broadband survey spectroscopy with spatial and temporal resolution and high-temperature Rosseland mean plasma opacity experiments. The new crystal spectrometer can be further improved by incorporating a CCD or X-ray streak camera into the instrument response model, and by adjusting the crystal placement to ensure continuous coverage of the spectral range and temporal resolution suited for HED physics experiments at the SGII laser facility.