1. Introduction
In the direct-drive (DD) inertial confinement fusion (ICF)[Reference Lindl1, Reference Atzeni and Meyer-ter-Vehn2] context a spherical capsule containing the deuterium–tritium (DT) nuclear fuel is irradiated by laser beams. The final goal is to generate energy gain via a nuclear fusion reaction: ![]() $\text{D}+\text{T}\rightarrow {\it\alpha}+\text{n}+17.6\ \text{MeV}$. The external shell of the capsule absorbs a fraction of the incoming laser energy producing a plasma; the plasma temperature (
$\text{D}+\text{T}\rightarrow {\it\alpha}+\text{n}+17.6\ \text{MeV}$. The external shell of the capsule absorbs a fraction of the incoming laser energy producing a plasma; the plasma temperature (![]() ${\approx}\text{keV}$) increase provides the outward expansion of the low-density corona and launches a series of inward shock waves. These shock waves compress the DT payload in a high-density shell that implodes and reaches stagnation. In the classical central ignition scheme, the high-density shell confines a small amount (
${\approx}\text{keV}$) increase provides the outward expansion of the low-density corona and launches a series of inward shock waves. These shock waves compress the DT payload in a high-density shell that implodes and reaches stagnation. In the classical central ignition scheme, the high-density shell confines a small amount (![]() ${\approx}10\ {\rm\mu}\text{g}$) of DT fuel – called a hot-spot – which is heated to high temperature (
${\approx}10\ {\rm\mu}\text{g}$) of DT fuel – called a hot-spot – which is heated to high temperature (![]() ${\approx}10\ \text{keV}$) and compressed to areal densities comparable with the
${\approx}10\ \text{keV}$) and compressed to areal densities comparable with the ![]() ${\it\alpha}$-particle range (
${\it\alpha}$-particle range (![]() $\int \!{\it\rho}\,dr\approx 0.3\ \text{g cm}^{-2}$), thus providing the ignition of the thermonuclear fusion reactions. Recently, the new shock ignition (SI) scheme[Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov3] has been proposed. In the SI scheme the fuel is first compressed by the usual DD technique, then a high-power laser pulse (
$\int \!{\it\rho}\,dr\approx 0.3\ \text{g cm}^{-2}$), thus providing the ignition of the thermonuclear fusion reactions. Recently, the new shock ignition (SI) scheme[Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov3] has been proposed. In the SI scheme the fuel is first compressed by the usual DD technique, then a high-power laser pulse (![]() ${\approx}$hundreds of TW) is used to launch a strong shock wave which provides the fuel ignition.
${\approx}$hundreds of TW) is used to launch a strong shock wave which provides the fuel ignition.
In all ICF schemes the capsule irradiation must be very uniform in order to inhibit growth of dangerous hydrodynamic instabilities that can prevent a successful fuel compression. In the promising SI scheme the requirements in terms of irradiation uniformity are less stringent in comparison with the classical central ignition scheme. Nevertheless, the irradiation uniformity represents one of the major constraints in ICF and a great deal of effort has been dedicated to its optimization.
In this paper we propose a numerical method to calculate the optimal laser intensity profiles of a generic number ![]() $N_{B}$ of laser beams irradiating a spherical target. Analytical optimization of the laser intensity profiles has been already performed for configurations based on the geometry of the Platonic solids[Reference Murakami4–Reference Murakami, Nishihara and Azechi7]. These analyses always provide axially symmetric laser intensity profiles where all the
$N_{B}$ of laser beams irradiating a spherical target. Analytical optimization of the laser intensity profiles has been already performed for configurations based on the geometry of the Platonic solids[Reference Murakami4–Reference Murakami, Nishihara and Azechi7]. These analyses always provide axially symmetric laser intensity profiles where all the ![]() $N_{B}$ laser intensities are equal. These solutions can be applied to laser configurations such as Gekko XII[Reference Azechi, Jitsuno, Kanabe, Katayama, Mima, Miyanaga, Nakai, Nakai, Nakaishi, Nakatsuka, Nishiguchi, Norrays, Setsuhara, Takagi, Yamanaka and Yamanaka8] (
$N_{B}$ laser intensities are equal. These solutions can be applied to laser configurations such as Gekko XII[Reference Azechi, Jitsuno, Kanabe, Katayama, Mima, Miyanaga, Nakai, Nakai, Nakaishi, Nakatsuka, Nishiguchi, Norrays, Setsuhara, Takagi, Yamanaka and Yamanaka8] (![]() $N_{B}=12$) or Omega[Reference Boehly, Brown, Craxton, Keck, Knauer, Kelly, Kessler, Kumpan, Loucks, Letzring, Marshall, McCrory, Morse, Seka, Soures and Verdon9] (60 beams) but are not suitable for laser configurations like the National Ignition Facility (NIF)[Reference Moses, Boyd, Remington, Keane and Al-Ayat10], the Laser MegaJoule (LMJ)[Reference Ebrardt and Chaput11] or the smaller Orion[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett12] facility where the locations of the beams are optimized for the indirect-drive[Reference Lindl, Amendt, Berger, Glendinning, Glenzer, Haan, Kauffman, Landen and Suter13] ICF scheme. Indeed, in these latter cases the optimal laser intensity profiles must be adapted to the laser configuration. As a consequence, the laser intensity profiles are not necessarily equal to each other or axially symmetric.
$N_{B}=12$) or Omega[Reference Boehly, Brown, Craxton, Keck, Knauer, Kelly, Kessler, Kumpan, Loucks, Letzring, Marshall, McCrory, Morse, Seka, Soures and Verdon9] (60 beams) but are not suitable for laser configurations like the National Ignition Facility (NIF)[Reference Moses, Boyd, Remington, Keane and Al-Ayat10], the Laser MegaJoule (LMJ)[Reference Ebrardt and Chaput11] or the smaller Orion[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett12] facility where the locations of the beams are optimized for the indirect-drive[Reference Lindl, Amendt, Berger, Glendinning, Glenzer, Haan, Kauffman, Landen and Suter13] ICF scheme. Indeed, in these latter cases the optimal laser intensity profiles must be adapted to the laser configuration. As a consequence, the laser intensity profiles are not necessarily equal to each other or axially symmetric.
2. Numerical method to optimize the intensity profiles
The proposed numerical method allows us to find the laser intensity profiles that optimize the illumination uniformity for a given laser configuration. These calculations are performed within an illumination model in which laser refraction is neglected, photons propagate linearly and the results only apply to the low-power foot-pulse that characterizes the first few ns of an ICF irradiation, the so-called imprint phase. Thus, the solution guarantees the uniformity of the first shock wavefront[Reference Temporal, Canaud, Garbett and Ramis14].
In the past, optimizing methods have usually been based on analytical or numerical parametric studies looking for the laser parameters that minimize the illumination nonuniformity. In contrast, in the present case a sort of predictor–corrector method is used: in a first step, trial laser intensity profiles are used to evaluate the – imperfect – irradiation of the spherical target; in a second step, the laser intensities are recalculated using the results of the first step in order to provide perfect illumination uniformity.
The model problem is characterized by a spherical target of radius ![]() $r_{0}$ irradiated by
$r_{0}$ irradiated by ![]() $N_{B}$ laser beams. The target centre is located at the origin of a Cartesian coordinate system
$N_{B}$ laser beams. The target centre is located at the origin of a Cartesian coordinate system ![]() $O(\boldsymbol{x},\boldsymbol{y},\boldsymbol{z})$ and the laser beam directions are characterized by the unitary vector
$O(\boldsymbol{x},\boldsymbol{y},\boldsymbol{z})$ and the laser beam directions are characterized by the unitary vector ![]() $\boldsymbol{r}_{n}$ defined by their polar angles
$\boldsymbol{r}_{n}$ defined by their polar angles ![]() ${\it\theta}_{n}$ and
${\it\theta}_{n}$ and ![]() ${\it\varphi}_{n}$ (see the details of the geometry in Figure 1). Each given elementary surface element of the target,
${\it\varphi}_{n}$ (see the details of the geometry in Figure 1). Each given elementary surface element of the target, ![]() $d\boldsymbol{s}=r_{0}^{2}\ d{\rm\Omega}$, is associated with a vector direction
$d\boldsymbol{s}=r_{0}^{2}\ d{\rm\Omega}$, is associated with a vector direction ![]() $\boldsymbol{r}({\it\theta},{\it\varphi})$ of co-latitude
$\boldsymbol{r}({\it\theta},{\it\varphi})$ of co-latitude ![]() ${\it\theta}\in [0-{\it\pi}]$ and longitude
${\it\theta}\in [0-{\it\pi}]$ and longitude ![]() ${\it\varphi}\in [0-2{\it\pi}]$. The laser intensity profile
${\it\varphi}\in [0-2{\it\pi}]$. The laser intensity profile ![]() $g_{n}(x^{\prime },y^{\prime })$ of the
$g_{n}(x^{\prime },y^{\prime })$ of the ![]() $N_{B}$ beams is defined in the planes orthogonal to the beam directions
$N_{B}$ beams is defined in the planes orthogonal to the beam directions ![]() $\boldsymbol{r}_{n}$. In these planes we define a secondary Cartesian coordinate system
$\boldsymbol{r}_{n}$. In these planes we define a secondary Cartesian coordinate system ![]() $O^{\prime }(x_{n}^{\prime },y_{n}^{\prime })$ where the orthogonal axes are given by the two versors:
$O^{\prime }(x_{n}^{\prime },y_{n}^{\prime })$ where the orthogonal axes are given by the two versors: ![]() $\boldsymbol{x}_{n}^{\prime }=(\boldsymbol{r}_{n}\wedge \boldsymbol{z})/|\boldsymbol{r}_{n}\wedge \boldsymbol{z}|$ and
$\boldsymbol{x}_{n}^{\prime }=(\boldsymbol{r}_{n}\wedge \boldsymbol{z})/|\boldsymbol{r}_{n}\wedge \boldsymbol{z}|$ and ![]() $\boldsymbol{y}_{n}^{\prime }=(\boldsymbol{x}_{n}^{\prime }\wedge \boldsymbol{r}_{n})/|\boldsymbol{x}_{n}^{\prime }\wedge \boldsymbol{r}_{n}|$. In this way the
$\boldsymbol{y}_{n}^{\prime }=(\boldsymbol{x}_{n}^{\prime }\wedge \boldsymbol{r}_{n})/|\boldsymbol{x}_{n}^{\prime }\wedge \boldsymbol{r}_{n}|$. In this way the ![]() $\boldsymbol{y}_{n}^{\prime }$-axis is located in the meridian plane containing the
$\boldsymbol{y}_{n}^{\prime }$-axis is located in the meridian plane containing the ![]() $n$th laser beam axis
$n$th laser beam axis ![]() $(\boldsymbol{r}_{n})$, while the
$(\boldsymbol{r}_{n})$, while the ![]() $\boldsymbol{x}^{\prime }$-axis is orthogonal to both
$\boldsymbol{x}^{\prime }$-axis is orthogonal to both ![]() $\boldsymbol{y}_{n}^{\prime }$ and
$\boldsymbol{y}_{n}^{\prime }$ and ![]() $\boldsymbol{r}_{n}$. Therefore, there is a one-to-one correspondence between a position
$\boldsymbol{r}_{n}$. Therefore, there is a one-to-one correspondence between a position ![]() $r_{0}\boldsymbol{r}({\it\theta},{\it\varphi})$ over the target surface and the corresponding coordinate
$r_{0}\boldsymbol{r}({\it\theta},{\it\varphi})$ over the target surface and the corresponding coordinate ![]() $x_{n}^{\prime }=r_{0}\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{x}_{n}^{\prime }$ and
$x_{n}^{\prime }=r_{0}\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{x}_{n}^{\prime }$ and ![]() $y_{n}^{\prime }=\ r_{0}\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{y}_{n}^{\prime }$, on the focal plane of the
$y_{n}^{\prime }=\ r_{0}\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{y}_{n}^{\prime }$, on the focal plane of the ![]() $n$th laser beam.
$n$th laser beam.
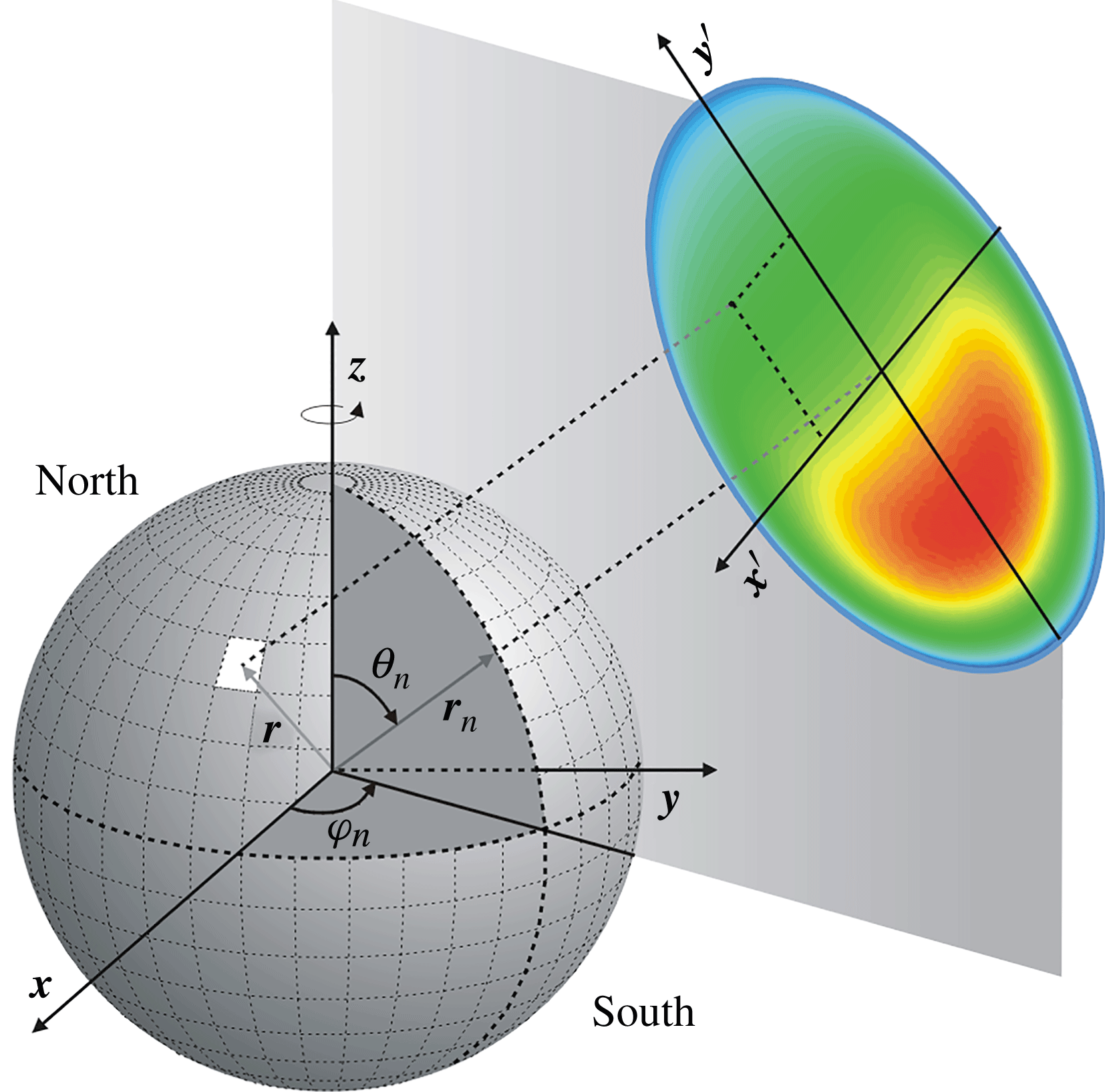
Figure 1. Spherical target and main coordinate system [![]() $O$]; vector direction
$O$]; vector direction ![]() $\boldsymbol{r}$ of a generic surface element and versor of the
$\boldsymbol{r}$ of a generic surface element and versor of the ![]() $n$th laser beam,
$n$th laser beam, ![]() $\boldsymbol{r}_{n}$; coordinate system [
$\boldsymbol{r}_{n}$; coordinate system [![]() $x^{\prime }$,
$x^{\prime }$, ![]() $y^{\prime }$] for the
$y^{\prime }$] for the ![]() $n$th laser intensity profile.
$n$th laser intensity profile.
The elementary surface ![]() $d\boldsymbol{s}$, located at the polar coordinates
$d\boldsymbol{s}$, located at the polar coordinates ![]() $({\it\theta},{\it\varphi})$, is irradiated by a given number (
$({\it\theta},{\it\varphi})$, is irradiated by a given number (![]() ${\leqslant}N_{B}$) of laser beams and receives a total laser intensity
${\leqslant}N_{B}$) of laser beams and receives a total laser intensity ![]() $I({\it\theta},{\it\varphi})$. This intensity is given by the contributions of all the incoming intensities associated with the laser profiles
$I({\it\theta},{\it\varphi})$. This intensity is given by the contributions of all the incoming intensities associated with the laser profiles ![]() $g_{n}(x^{\prime },y^{\prime })$ multiplied by the scalar product
$g_{n}(x^{\prime },y^{\prime })$ multiplied by the scalar product ![]() $(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n})$ to account for projection of the surface area. Thus, for the
$(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n})$ to account for projection of the surface area. Thus, for the ![]() $N_{B}$ laser beams the irradiation of the spherical target surface is given by
$N_{B}$ laser beams the irradiation of the spherical target surface is given by
where the scalar product ![]() $(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n})$ is set to zero when it assumes a negative value. The exponent
$(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n})$ is set to zero when it assumes a negative value. The exponent ![]() ${\it\beta}$ must be larger than or equal to one and account for the specific assumption on the laser–capsule coupling, e.g., setting
${\it\beta}$ must be larger than or equal to one and account for the specific assumption on the laser–capsule coupling, e.g., setting ![]() ${\it\beta}=2$ recovers the hypothesis of the laser absorption assumed by Schmitt[Reference Schmitt6]. Hereafter we use the standard illumination model for which
${\it\beta}=2$ recovers the hypothesis of the laser absorption assumed by Schmitt[Reference Schmitt6]. Hereafter we use the standard illumination model for which ![]() ${\it\beta}=1$. For a given laser intensity profile
${\it\beta}=1$. For a given laser intensity profile ![]() $g_{n}$, direct application of the illumination model provides the laser intensity
$g_{n}$, direct application of the illumination model provides the laser intensity ![]() $I({\it\theta},{\it\varphi})$ used to calculate the root-mean-square (r.m.s.) deviation
$I({\it\theta},{\it\varphi})$ used to calculate the root-mean-square (r.m.s.) deviation ![]() ${\it\sigma}$, which is assumed as a measure of the target irradiation nonuniformity:
${\it\sigma}$, which is assumed as a measure of the target irradiation nonuniformity:
where ![]() $I_{a}$ is the average intensity calculated over the whole sphere.
$I_{a}$ is the average intensity calculated over the whole sphere.
Of course, the condition to obtain ![]() ${\it\sigma}=0$ is to generate a perfectly uniform irradiation over the whole target surface, i.e., to realize
${\it\sigma}=0$ is to generate a perfectly uniform irradiation over the whole target surface, i.e., to realize ![]() $I({\it\theta},{\it\varphi})=I_{0}$, where
$I({\it\theta},{\it\varphi})=I_{0}$, where ![]() $I_{0}$ is the desired intensity over the target surface. This could be done by a simple re-normalization of the laser intensity profiles, by
$I_{0}$ is the desired intensity over the target surface. This could be done by a simple re-normalization of the laser intensity profiles, by
Now, substituting the old intensity profiles ![]() $g_{n}$ with the new ones
$g_{n}$ with the new ones ![]() $g_{n}^{\prime }$ in Equation (1) will provide
$g_{n}^{\prime }$ in Equation (1) will provide ![]() $I({\it\theta},{\it\varphi})=I_{0}$ and therefore
$I({\it\theta},{\it\varphi})=I_{0}$ and therefore ![]() ${\it\sigma}=0$. A necessary condition to realize the uniform constant intensity illumination –
${\it\sigma}=0$. A necessary condition to realize the uniform constant intensity illumination – ![]() $I({\it\theta},{\it\varphi})=I_{0}$ – over the whole target surface is that each elementary surface of the target must be irradiated by at least one laser beam. Indeed, if some part of the target is not irradiated at all, e.g., for
$I({\it\theta},{\it\varphi})=I_{0}$ – over the whole target surface is that each elementary surface of the target must be irradiated by at least one laser beam. Indeed, if some part of the target is not irradiated at all, e.g., for ![]() $N_{B}=1$, the method fails. Thus, the optimization is obtained in two steps: first, by means of a set of trial laser intensity profiles
$N_{B}=1$, the method fails. Thus, the optimization is obtained in two steps: first, by means of a set of trial laser intensity profiles ![]() $g_{n}$, the target irradiation
$g_{n}$, the target irradiation ![]() $I({\it\theta},{\it\varphi})$ is calculated, and then these trial intensities are corrected – by using Equation (3) – to provide the optimized profiles
$I({\it\theta},{\it\varphi})$ is calculated, and then these trial intensities are corrected – by using Equation (3) – to provide the optimized profiles ![]() $g_{n}^{\prime }$. In these calculations the target surface is subdivided into
$g_{n}^{\prime }$. In these calculations the target surface is subdivided into ![]() $180\times 360$ elementary elements and thus the method provides a discrete number of coordinates
$180\times 360$ elementary elements and thus the method provides a discrete number of coordinates ![]() $(x^{\prime },y^{\prime })$ where the laser intensity profiles
$(x^{\prime },y^{\prime })$ where the laser intensity profiles ![]() $g_{n}^{\prime }$ are defined. These data are used to estimate the intensity profiles,
$g_{n}^{\prime }$ are defined. These data are used to estimate the intensity profiles, ![]() $g_{n}^{\prime }$, on the focal plane where the spatial resolution has been set to
$g_{n}^{\prime }$, on the focal plane where the spatial resolution has been set to ![]() $dx^{\prime }=dy^{\prime }=r_{0}/200$, which provides a total of
$dx^{\prime }=dy^{\prime }=r_{0}/200$, which provides a total of ![]() $400\times 400$ values for the laser intensity profiles. With these values the irradiation nonuniformities
$400\times 400$ values for the laser intensity profiles. With these values the irradiation nonuniformities ![]() ${\it\sigma}$ for the cases calculated in this paper are kept below
${\it\sigma}$ for the cases calculated in this paper are kept below ![]() ${\it\sigma}=10^{-4}$. It is worth noticing that an increase of the resolution on the intensity profile or a reduction of the number of elementary surfaces on the target surface increases the precision of the calculation, providing a smaller
${\it\sigma}=10^{-4}$. It is worth noticing that an increase of the resolution on the intensity profile or a reduction of the number of elementary surfaces on the target surface increases the precision of the calculation, providing a smaller ![]() ${\it\sigma}$.
${\it\sigma}$.
The optimal laser intensity profiles, solution of the coupled Equations (3) and (1), depend on the choice of trial intensities ![]() $g_{n}$; therefore, the set of solutions is not unique. The trial intensity must be well posed in order to generate reasonably final optimized profiles. Hereafter, we use the trial intensity given by the scalar product:
$g_{n}$; therefore, the set of solutions is not unique. The trial intensity must be well posed in order to generate reasonably final optimized profiles. Hereafter, we use the trial intensity given by the scalar product: ![]() $g_{n}(x^{\prime },y^{\prime })=|\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n}|=[r_{0}^{2}-x^{^{\prime }2}-y^{^{\prime }2}]^{1/2}/r_{0}$; a higher intensity is assigned to the beam centre and it vanishes at the target border; the aim of this choice is to look for a solution
$g_{n}(x^{\prime },y^{\prime })=|\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n}|=[r_{0}^{2}-x^{^{\prime }2}-y^{^{\prime }2}]^{1/2}/r_{0}$; a higher intensity is assigned to the beam centre and it vanishes at the target border; the aim of this choice is to look for a solution ![]() $g_{n}^{\prime }$ that maximizes the laser–capsule coupling. It is worth noticing that although the trial beams are axially symmetric, the final solution will not be symmetric, as we will see later. Moreover, in these calculations we used the same trial function – the scalar product – for all the
$g_{n}^{\prime }$ that maximizes the laser–capsule coupling. It is worth noticing that although the trial beams are axially symmetric, the final solution will not be symmetric, as we will see later. Moreover, in these calculations we used the same trial function – the scalar product – for all the ![]() $g_{n}$; nevertheless, the method applies equally well even if the trial functions are different for each laser beam.
$g_{n}$; nevertheless, the method applies equally well even if the trial functions are different for each laser beam.
3. Profiles for a two-ring 2D irradiation configuration
As a first example we considered a two-dimensional (2D) axially symmetric laser configuration where the beams can be approximated by two annular rings at the co-latitudes ![]() ${\it\theta}_{1}$ and
${\it\theta}_{1}$ and ![]() ${\it\theta}_{2}={\it\pi}-{\it\theta}_{1}$; this is achieved by imposing that
${\it\theta}_{2}={\it\pi}-{\it\theta}_{1}$; this is achieved by imposing that ![]() $I({\it\theta},{\it\varphi})\equiv I({\it\theta})=[\int \!I({\it\theta},{\it\varphi})d{\it\phi}]/(2{\it\pi})$. The two optimal intensity profiles
$I({\it\theta},{\it\varphi})\equiv I({\it\theta})=[\int \!I({\it\theta},{\it\varphi})d{\it\phi}]/(2{\it\pi})$. The two optimal intensity profiles ![]() $g_{1}^{\prime }({\it\theta}_{1})$ and
$g_{1}^{\prime }({\it\theta}_{1})$ and ![]() $g_{2}^{\prime }({\it\theta}_{2})$ have been calculated for different values of
$g_{2}^{\prime }({\it\theta}_{2})$ have been calculated for different values of ![]() ${\it\theta}_{1}$. In this perfectly symmetric case, the two solutions are equal and are just rotated by
${\it\theta}_{1}$. In this perfectly symmetric case, the two solutions are equal and are just rotated by ![]() $180^{\circ }$,
$180^{\circ }$, ![]() $g_{1}^{\prime }(x^{\prime },y^{\prime })=g_{2}(x^{\prime },-y^{\prime })$. The laser intensity profiles
$g_{1}^{\prime }(x^{\prime },y^{\prime })=g_{2}(x^{\prime },-y^{\prime })$. The laser intensity profiles ![]() $g_{1}^{\prime }$ normalized to one and corresponding to the annular ring of the north hemisphere are shown in Figure 2 for different polar angles,
$g_{1}^{\prime }$ normalized to one and corresponding to the annular ring of the north hemisphere are shown in Figure 2 for different polar angles, ![]() ${\it\theta}_{1}$.
${\it\theta}_{1}$.
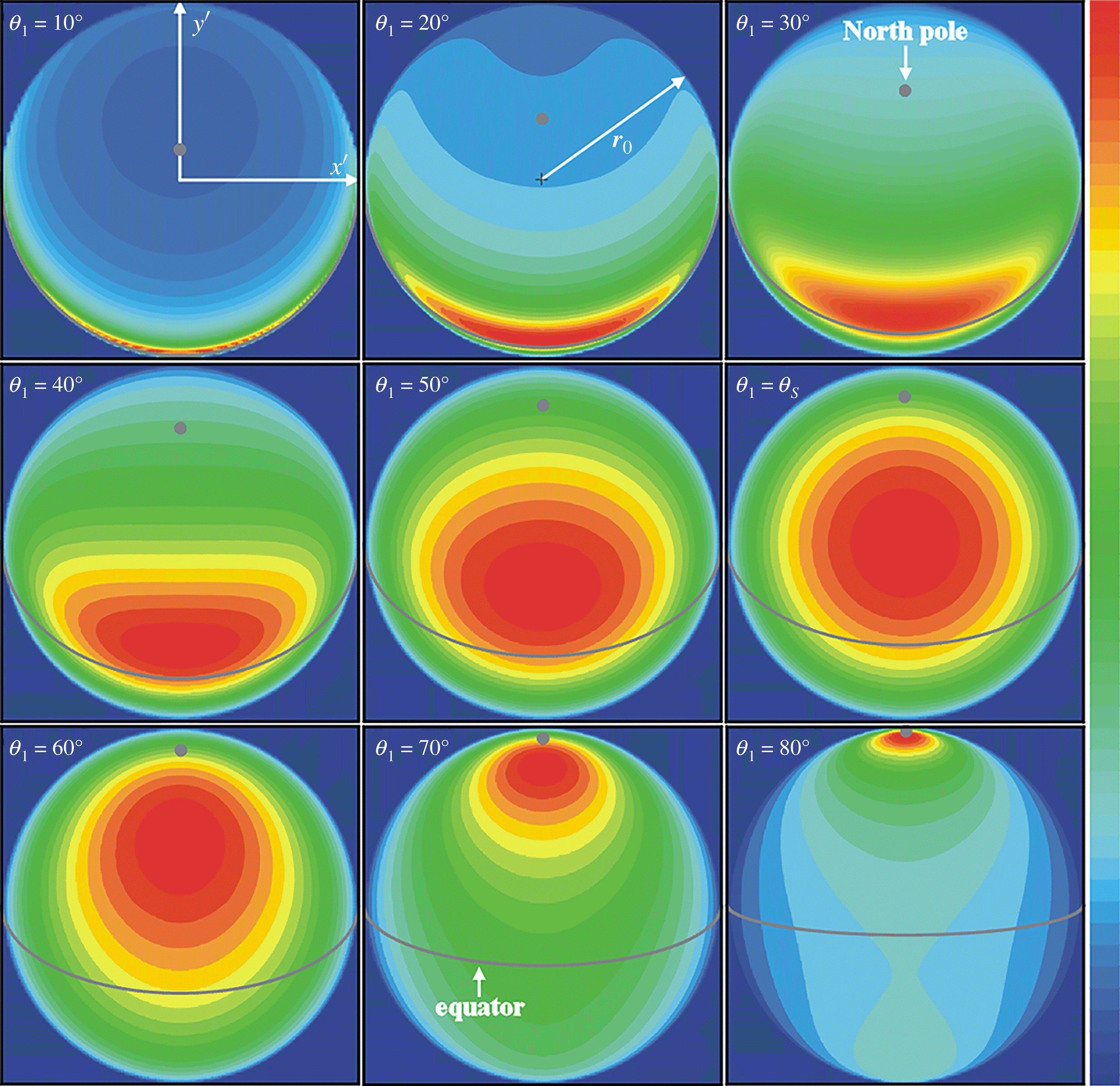
Figure 2. Optimal laser intensity profiles ![]() $g_{1}^{\prime }(x^{\prime },y^{\prime })$ (north hemisphere) for an axially symmetric beam configuration. The intensity profiles have been normalized to one (
$g_{1}^{\prime }(x^{\prime },y^{\prime })$ (north hemisphere) for an axially symmetric beam configuration. The intensity profiles have been normalized to one (![]() $g_{1}^{\prime }/\text{Max}[g_{1}^{\prime }]$) and the scale colour ranges from 0 to 1. Full dots correspond to the north pole and the grey curve is the equator projection on the focal planes.
$g_{1}^{\prime }/\text{Max}[g_{1}^{\prime }]$) and the scale colour ranges from 0 to 1. Full dots correspond to the north pole and the grey curve is the equator projection on the focal planes.
In these frames the grey curves show the projection of the equator in the focal plane, while the full grey dots localize the projection of the north pole. In these images the laser intensity has been normalized to 1 and the colour scale ranges from 0 to 1. For small polar angles, e.g., ![]() ${\it\theta}_{1}=10^{\circ }$, the laser beams are closer to the
${\it\theta}_{1}=10^{\circ }$, the laser beams are closer to the ![]() $z$-axis, thus the surfaces of the polar areas are highly irradiated with a nearly orthogonal angle of incidence; on the contrary, for larger angles, it is the equatorial belt that will be over-irradiated in comparison with the polar regions. To compensate for this unbalanced irradiation the optimal laser intensity profile provides different intensities in correspondence to the equatorial and polar target areas. Specifically, at smaller angles (see, e.g.,
$z$-axis, thus the surfaces of the polar areas are highly irradiated with a nearly orthogonal angle of incidence; on the contrary, for larger angles, it is the equatorial belt that will be over-irradiated in comparison with the polar regions. To compensate for this unbalanced irradiation the optimal laser intensity profile provides different intensities in correspondence to the equatorial and polar target areas. Specifically, at smaller angles (see, e.g., ![]() ${\it\theta}_{1}=10^{\circ }$) a maximum intensity is directed towards the equator, while at larger angles (e.g.,
${\it\theta}_{1}=10^{\circ }$) a maximum intensity is directed towards the equator, while at larger angles (e.g., ![]() ${\it\theta}_{1}=80^{\circ }$) the laser intensity is higher in proximity to the polar areas. It is worth noticing that the laser intensity profile becomes circular (axially symmetric) when
${\it\theta}_{1}=80^{\circ }$) the laser intensity is higher in proximity to the polar areas. It is worth noticing that the laser intensity profile becomes circular (axially symmetric) when ![]() ${\it\theta}_{1}$ equals the Schmitt angle
${\it\theta}_{1}$ equals the Schmitt angle ![]() ${\it\theta}_{1}={\it\theta}_{S}=54.7^{\circ }$ (Ref. [Reference Schmitt6]). This is not surprising; indeed, as shown by Schmitt, the angle
${\it\theta}_{1}={\it\theta}_{S}=54.7^{\circ }$ (Ref. [Reference Schmitt6]). This is not surprising; indeed, as shown by Schmitt, the angle ![]() ${\it\theta}_{S}$ is the best co-latitude if the axisymmetric beam intensity profile is given by
${\it\theta}_{S}$ is the best co-latitude if the axisymmetric beam intensity profile is given by ![]() $I_{0}\cos ({\it\gamma})$ with
$I_{0}\cos ({\it\gamma})$ with ![]() ${\it\beta}=1$.
${\it\beta}=1$.
4. Optimal profile for some LMJ configurations
An LMJ configuration consisting of 40 quads has been considered in this paper. The quad of the LMJ is composed of a bundle of four laser beams and provides a maximum laser energy (power) of 30 kJ (10 TW) at ![]() $3{\it\omega}$ (
$3{\it\omega}$ (![]() ${\it\lambda}=351\ \text{nm}$). The polar coordinates of the 40 quads are shown in Figure 3. Here, we assume that each quad can be characterized by a single beam with a given laser intensity profile. Four configurations have been considered: (A) a total of four quads (two in the second ring and two in the third ring), labelled A in Figure 3; (B) five quads in the second ring and five in the third ring (ten quads, labelled B); (C) a total of eight quads, two quads in each of the four rings (red quads for the north hemisphere); (D) five quads in each ring (blue quads for the south hemisphere) for a total of 20 quads.
${\it\lambda}=351\ \text{nm}$). The polar coordinates of the 40 quads are shown in Figure 3. Here, we assume that each quad can be characterized by a single beam with a given laser intensity profile. Four configurations have been considered: (A) a total of four quads (two in the second ring and two in the third ring), labelled A in Figure 3; (B) five quads in the second ring and five in the third ring (ten quads, labelled B); (C) a total of eight quads, two quads in each of the four rings (red quads for the north hemisphere); (D) five quads in each ring (blue quads for the south hemisphere) for a total of 20 quads.
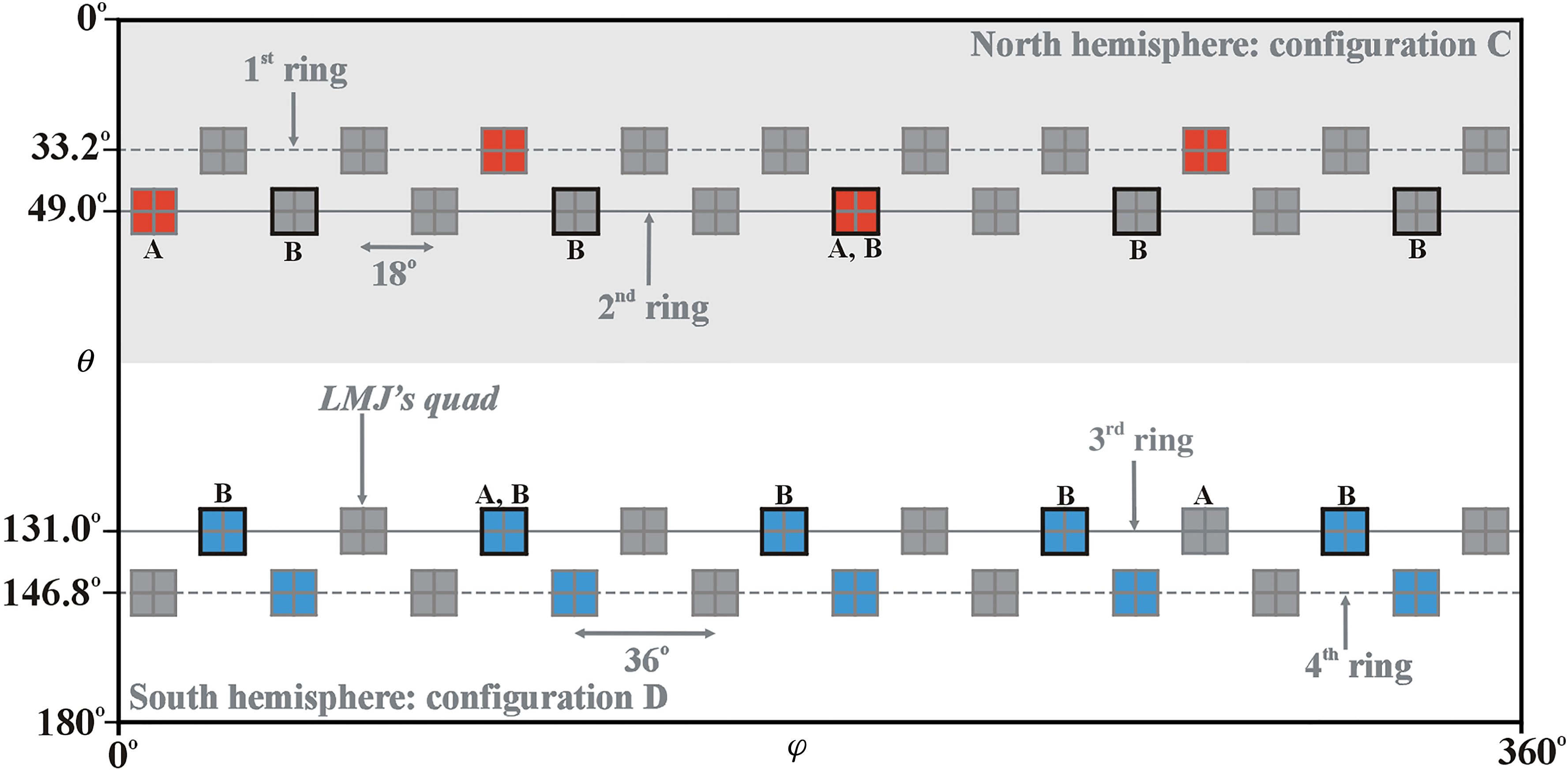
Figure 3. Polar coordinates of 40 quads of the LMJ facility. Quads for the configurations A and B; red quads of the north hemisphere (C) and blue quads of the south hemisphere (D).
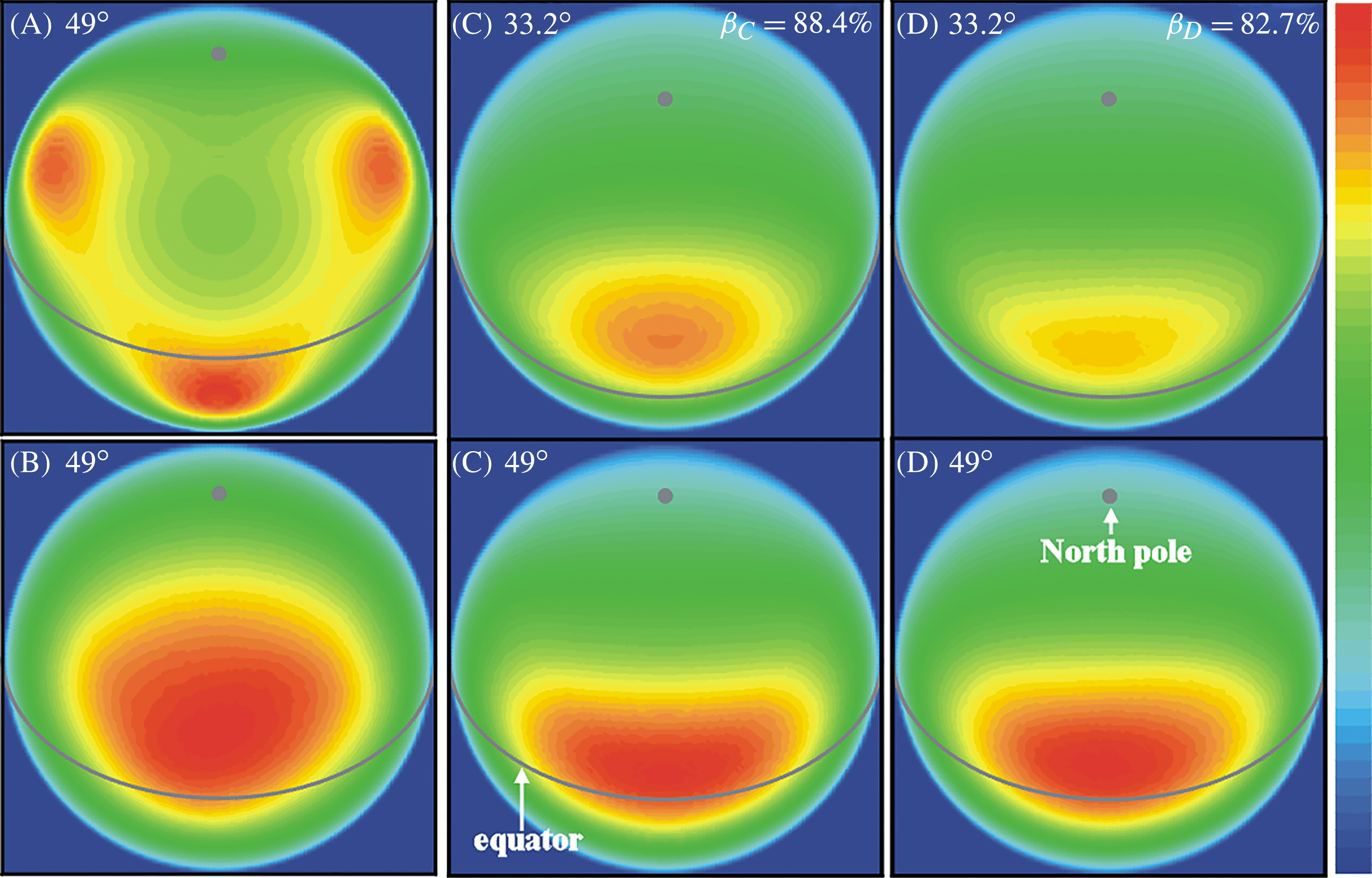
Figure 4. Optimal laser intensity profiles ![]() $g_{n}^{\prime }$ normalized to one (north hemisphere) for the LMJ configurations A–D. The power imbalance is given by the parameter
$g_{n}^{\prime }$ normalized to one (north hemisphere) for the LMJ configurations A–D. The power imbalance is given by the parameter ![]() ${\it\beta}$ and the laser intensity scale colour varies linearly from 0 to 1.
${\it\beta}$ and the laser intensity scale colour varies linearly from 0 to 1.
The optimization method has been applied to the four laser configurations A–D. As above, all the ![]() $N_{B}$ trial intensities are given by the scalar product:
$N_{B}$ trial intensities are given by the scalar product: ![]() $g_{n}(x^{\prime },y^{\prime })=(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n})$. The optimal intensity profiles
$g_{n}(x^{\prime },y^{\prime })=(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n})$. The optimal intensity profiles ![]() $g_{n}^{\prime }$ provided for these configurations are shown in Figure 4. These profiles have been normalized to one by dividing the intensities by their maximum value:
$g_{n}^{\prime }$ provided for these configurations are shown in Figure 4. These profiles have been normalized to one by dividing the intensities by their maximum value: ![]() $\text{Max}[g^{\prime }]_{A}=1.52I_{0}$;
$\text{Max}[g^{\prime }]_{A}=1.52I_{0}$; ![]() $\text{Max}[g^{\prime }]_{B}=0.62I_{0}$;
$\text{Max}[g^{\prime }]_{B}=0.62I_{0}$; ![]() $\text{Max}[g^{\prime }]_{C}=0.92I_{0}$;
$\text{Max}[g^{\prime }]_{C}=0.92I_{0}$; ![]() $\text{Max}[g^{\prime }]_{D}=0.38I_{0}$. These images correspond to the beams of the north hemisphere, while those of the south hemisphere are obtained by a rotation of
$\text{Max}[g^{\prime }]_{D}=0.38I_{0}$. These images correspond to the beams of the north hemisphere, while those of the south hemisphere are obtained by a rotation of ![]() $180^{\circ }$. In these irradiation configurations the optimal laser intensity profiles provide an r.m.s. irradiation nonuniformity
$180^{\circ }$. In these irradiation configurations the optimal laser intensity profiles provide an r.m.s. irradiation nonuniformity ![]() ${\it\sigma}$ lower than
${\it\sigma}$ lower than ![]() $10^{-4}$.
$10^{-4}$.
The configuration A has only two beams per hemisphere, and their optimized intensity profile shows three zones at higher intensity: one located below the equator and the other two closer to the pole. The intensity profile for the ten beams of configuration B is shown in Figure 4 (bottom left image). In this case the higher intensity is situated between the beam’s centre and the equator position and the shape of the laser intensity is not symmetric due to the rotation of ![]() $18^{\circ }$ between the hemispheres. In the configurations C and D the numerical method provides two intensity profiles: one for the beams of the first ring and a second for those of the second ring. In these two cases the calculations provide similar shapes. Moreover, the numerical results naturally introduce a power imbalance ratio between the maximum beam intensities:
$18^{\circ }$ between the hemispheres. In the configurations C and D the numerical method provides two intensity profiles: one for the beams of the first ring and a second for those of the second ring. In these two cases the calculations provide similar shapes. Moreover, the numerical results naturally introduce a power imbalance ratio between the maximum beam intensities: ![]() ${\it\beta}_{C}=I_{\text{Max}}(49^{\circ })/I_{\text{Max}}(33.2^{\circ })=88.4\%$ and
${\it\beta}_{C}=I_{\text{Max}}(49^{\circ })/I_{\text{Max}}(33.2^{\circ })=88.4\%$ and ![]() ${\it\beta}_{D}=82.7$. It is worth noticing that these optimum intensities are located off-centre. This could be regarded as the application of the polar direct-drive[Reference Skupsky, Marozas, Craxton, Betti, Collins, Delettrez, Goncharov, McKenty, Radha, Knauer, Marshall, Harding, Kilkenny, Meyerhofer, Sangster and McCrory15] (PDD) technique where a centred laser intensity profile moves towards the equator to compensate the over-irradiation of the polar zones[Reference Temporal, Canaud, Garbett and Ramis16]. In addition, it has been shown[Reference Temporal, Canaud, Garbett, Philippe and Ramis17, Reference Temporal, Canaud, Garbett and Ramis18] that for the configurations C and D elliptical intensity profiles provide a more uniform irradiation than circular ones. The current calculations confirm this trend and show that the optimal intensity profiles are closer to an elliptical shape – characteristic of an indirect-drive installation – rather than circular profiles.
${\it\beta}_{D}=82.7$. It is worth noticing that these optimum intensities are located off-centre. This could be regarded as the application of the polar direct-drive[Reference Skupsky, Marozas, Craxton, Betti, Collins, Delettrez, Goncharov, McKenty, Radha, Knauer, Marshall, Harding, Kilkenny, Meyerhofer, Sangster and McCrory15] (PDD) technique where a centred laser intensity profile moves towards the equator to compensate the over-irradiation of the polar zones[Reference Temporal, Canaud, Garbett and Ramis16]. In addition, it has been shown[Reference Temporal, Canaud, Garbett, Philippe and Ramis17, Reference Temporal, Canaud, Garbett and Ramis18] that for the configurations C and D elliptical intensity profiles provide a more uniform irradiation than circular ones. The current calculations confirm this trend and show that the optimal intensity profiles are closer to an elliptical shape – characteristic of an indirect-drive installation – rather than circular profiles.
The NIF configuration has been also analysed, providing four optimal laser intensity profiles. In this case the 48 quads of the NIF facility are located at four rings in each hemisphere: four quads at ![]() ${\it\theta}_{1}=23.5^{\circ }$, four at
${\it\theta}_{1}=23.5^{\circ }$, four at ![]() ${\it\theta}_{2}=30.0^{\circ }$, eight at
${\it\theta}_{2}=30.0^{\circ }$, eight at ![]() ${\it\theta}_{3}=44.5^{\circ }$ and eight at
${\it\theta}_{3}=44.5^{\circ }$ and eight at ![]() ${\it\theta}_{4}=50.0^{\circ }$. The method of optimization, initialized with the trial intensity
${\it\theta}_{4}=50.0^{\circ }$. The method of optimization, initialized with the trial intensity ![]() $g_{n}(x^{\prime },y^{\prime })=(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n})$, produces intensity profiles similar to those found for configuration D. These calculations also supply the optimal power imbalances
$g_{n}(x^{\prime },y^{\prime })=(\boldsymbol{r}\boldsymbol{\cdot }\boldsymbol{r}_{n})$, produces intensity profiles similar to those found for configuration D. These calculations also supply the optimal power imbalances ![]() ${\it\beta}_{1}=69.3\%$,
${\it\beta}_{1}=69.3\%$, ![]() ${\it\beta}_{2}=77.2\%$,
${\it\beta}_{2}=77.2\%$, ![]() ${\it\beta}_{3}=94\%$, while the maximum power (
${\it\beta}_{3}=94\%$, while the maximum power (![]() ${\it\beta}_{4}=1$) is assigned to the laser beams located at the larger angle
${\it\beta}_{4}=1$) is assigned to the laser beams located at the larger angle ![]() ${\it\theta}_{4}=50.0^{\circ }$.
${\it\theta}_{4}=50.0^{\circ }$.
5. Conclusions
In conclusion, we developed a general method to calculate the optimal laser intensity profiles that optimize the illumination nonuniformity of a spherical target. The method can be used for any DD laser configuration accounting for a general number ![]() $N_{B}$ of laser beams, provided that the beams irradiate the whole target surface. In some sense this is a kind of predictor–corrector method that consists of two steps: firstly, initialized by a set of
$N_{B}$ of laser beams, provided that the beams irradiate the whole target surface. In some sense this is a kind of predictor–corrector method that consists of two steps: firstly, initialized by a set of ![]() $N_{B}$ trial laser intensity profiles, the imperfect surface irradiation is calculated; then, the beam profiles are recalculated in order to correct the previously estimated nonuniform illumination.
$N_{B}$ trial laser intensity profiles, the imperfect surface irradiation is calculated; then, the beam profiles are recalculated in order to correct the previously estimated nonuniform illumination.
A set of four laser configurations based on the LMJ facility has been considered. In these cases, the optimal intensity profiles have been individuated using axially symmetric trial profiles. The resulting optimal intensity profiles are not axially symmetric and their shapes look like to those envisaged by the PDD technique; in addition, these calculations also predict the optimal beam-to-beam power imbalance. These results assume perfect beam-to-beam power imbalance, neglecting laser pointing errors and target positioning uncertainties; deviation from these idealized assumptions would damage the uniformity of the target illumination.
Acknowledgements
M.T. and B.C. express their thanks to Daniel Bouche for the support given to this work. R.R. was partially supported by the EURATOM/CIEMAT association in the framework of the ‘IFE Keep-in-Touch Activities’.







