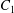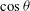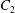Off-axis Fresnel numbers in laser systems

Abstract

The physical meaning and essence of Fresnel numbers are discussed, and two definitions of these numbers for off-axis optical systems are proposed. The universal Fresnel number is found to be $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}N=(a^{2}/\lambda z ) \ast C_{1} +C_{2} $. The Rayleigh–Sommerfeld nonparaxial diffraction formula states that a simple analytical formula for the nonparaxial intensity distribution after a circular aperture can be obtained. Theoretical derivations and numerical calculations reveal that the first correction factor $C_{1} $ is equal to $\cos \theta $ and the second factor $C_{2} $ is a function of the incident wavefront and the shape of the diffractive aperture. Finally, some diffraction phenomena in off-axis optical systems are explained by the off-axis Fresnel number.

1. Introduction

Diffraction fields can be exactly solved by the Fresnel diffraction integral, but the calculation is highly complicated. The Fresnel number $N$ allows a qualitative or semi-quantitative analysis of the diffraction field, thereby providing a clear physical picture and intuitive method. Some examples are the connections between the Fresnel number and the focal shift^[1], the confirmation and application of the $\pi $ phase jump in the boundary diffraction wave^[2] and the Fresnel patterns in a system with a lens^[3]; these examples are analyzed quantitatively by the Fresnel number.

If a plane wave is normally incident upon a circular aperture, the standard Fresnel number is defined as^[4]

$$\begin{equation*} N_{st} =\frac {a^{2}}{\lambda z}, \end{equation*}$$

where $a$ is the radius of the circular aperture, $\lambda $ is the wavelength of the incident light, and $z$ denotes the distance from the diffractive aperture to the axial point under the conditions $a\gg \lambda ,z\gg a$.

The essence of the Fresnel number is the variation of the optical path in the propagation; the physical meaning is the number of Fresnel half-wave zones included in the diffractive aperture^[4]. The diffracted field is analyzed by the nature of the central point using the Fresnel number. For axially diffracted fields, the diffraction pattern changes with the distance in the Fresnel diffraction region; maximal and minimal on-axis intensities are observed with a parity change in $N$. In the Fraunhofer diffraction region ($N < 1$) the rays produced by diffractive apertures are superimposed at the central point with almost the same phase; hence, the diffraction pattern remains stable^[3].

The Fresnel number can be expanded to the off-axis point; the number of Fresnel half-wave zones for this point can be calculated to elucidate the properties of radially diffracted fields. For example, the locations of the minimal and secondary maximal intensities in the radially diffracted field of a grating can be obtained by the half-wave zone method^[5].

Light beams fall under normal or oblique incidences in optical systems, and their Fresnel number of normal incidence is given in Refs. [6–8]. The application of the Fresnel number in high power laser systems has been discussed in Ref. [9]. The physical meaning and application of complex Fresnel numbers in Gaussian beams diffracted by hard apertures have also been studied^[10]. However, oblique incidence^[11] and tilted optical elements^[12] are often used in practice; hence, a universal Fresnel number to explain the diffraction phenomena in an off-axis optical system is necessary. In this paper an expression for the off-axis Fresnel number is provided through theoretical derivations and numerical calculations.

Figure 1. Diagram representing off-axis beams.

Figure 2. Beam propagation in the (a) meridian plane and (b) the sagittal surface.

2. Definition of the off-axis Fresnel number

The Fresnel number is defined in two ways. First, the number physically represents the optical path difference between a wavelet from the aperture edge to the observation point and a wavelet from the aperture center to the observation point; the path difference is then divided by $\lambda /2$^[3]. Second, the positions of extreme axial intensities correspond to integral Fresnel numbers^[7]. Odd and even values of $N$ yield the maximum and minimum axial intensities respectively.

By taking the direction of the center wavelet as the auxiliary axis $L$, the focal point $C$ is defined as the intersection of the auxiliary axis and the observation screen (Figure 1); $\theta $ is the angle between the incident beam and the optical axis. The diffractive aperture is on the $(x_{1} ,y_{1})$ plane and the calculated diffraction field is on the $(x,y)$ plane, which is parallel to the $(x_{1} ,y_{1})$ plane and has a normal distance $z$ from it. Based on this point, the off-axis Fresnel number can be obtained using two methods. One is through the basic definition of the Fresnel number: the off-axis Fresnel number can be expressed as $N=2\Delta /\lambda $, where $\Delta $ is the optical path difference between the wavelet of the aperture edge to the focal point and the wavelet of the aperture center to the focal point. The other is by defining an equivalent off-axis Fresnel number: the integral Fresnel numbers correspond to locations of intensity extrema on the auxiliary axis. The axial position $z$ of the intensity extrema is obtained through the $I\mbox{--}z$ curve ($I$ is the normalized intensity on the auxiliary axis) derived from numerical calculations; $z$ is sorted in descending order, the values of which correspond to Fresnel numbers $1,2,\ldots, N$ ($N$ is the number of intensity extrema) which are obtained by fitting the $N\mbox{--}z$ curve. The off-axis Fresnel number is then corrected as

(1)$$\begin{equation} N=N_{st} C_{1} +C_{2} , \label {eqn1} \end{equation}$$

where $C_{1} $ is the correction factor determined by the incident angle and $C_{2} $ is the correction factor determined by the incident wavefront and the shape of the diffractive aperture.

3. Resolution of the expression for the off-axis Fresnel number

In the case of a plane wave, the off-axis Fresnel number is obtained through theoretical derivations and numerical calculations. The scope of application is discussed by comparison with the result obtained through numerical calculations.

3.1. Theoretical derivation

The coordinate system is chosen so that the incident plane wave is perpendicular to $x_{1} $, subtends an angle of $\pi +\theta /2$ with the $y_{1} $ axis in the counterclockwise direction and forms an angle of $\theta $ with the optical axis $z$. Taylor series expansion is carried out around $L\ (L=z /\cos \theta )$ if $L$ is taken as the auxiliary axis. The meridian plane comprises axes $L$ and $z$; the sagittal surface consists of axes $L$ and $x_{1}$. The optical path differences are calculated separately in these two surfaces (Figure 2).

3.1.1. Meridian plane

As shown in Figure 2(a), a plane wave is obliquely incident on the aperture, and the line DEB is the intersection line of the equiphase surface and the meridian plane. Optical paths before line DEB are equal, so only optical paths after it have to be calculated.

(1) The optical path of the upper wavelet (DAC).

$$\begin{eqnarray*} L_{1m} &=& DA+AC=2a\sin \theta + [z^{2}+(z\tan \theta -a )^{2}]^{\frac {1}{2}} \\ &=& 2a\sin \theta + \frac {z}{\cos \theta }\biggl [1 +\! \biggl (\frac {a}{z/\cos \theta } \biggr )^{2} \!-\!\biggl (\frac {a}{z/\sin 2\theta }\biggr )\biggr ]^{\frac {1}{2}} \\ &\approx & a\sin \theta +\frac {z}{\cos \theta }+\frac {a^{2}\cos \theta }{2z}. \end{eqnarray*}$$

When $a\ll z$ the last two items in the bracket are much less than 1, so Taylor series expansion is performed around $L$ ($L=z/\cos \theta $).

(2) The optical path of the lower wavelet (BC).

$$\begin{eqnarray*} L_{2m} &=& BC= [z^{2}+ (z\tan \theta +a )^{2}]^{\frac {1}{2}} \\ &=& \frac {z}{\cos \theta }\biggl [1+ \biggl (\frac {a}{z/\cos \theta } \biggr )^{2}+ \biggl (\frac {a}{z/\sin 2\theta }\biggr )\biggr ]^{\frac {1}{2}} \\ &\approx & a\sin \theta +\frac {z}{\cos \theta }+\frac {a^{2}\cos \theta }{2z}\quad (a\ll z). \end{eqnarray*}$$

(3) The optical path of the center wavelet (EC).

$$\begin{equation*} L_{0m} =EC=a\sin \theta +\frac {z}{\cos \theta }. \end{equation*}$$

It can be seen that the optical paths on the upper and lower edges are equal $(L_{m} =L_{1m} =L_{2m})$; the difference between optical paths on the edge and on the center is given as

$$\begin{equation*} \Delta _{m} =L_{m} -L_{0m} =\frac {a^{2}\cos \theta }{2z}. \end{equation*}$$

3.1.2. Sagittal surface

(1) The optical paths of the wavelets from the upper and lower edges are equal (as shown in Figure 2(b)).

$$\begin{equation*} L_{s} = \biggl [\biggl (\frac {z}{\cos \theta } \biggr )^{2}+a^{2}\biggr ]^{\frac {1}{2}} \approx \frac {z}{\cos \theta }+\frac {a^{2}\cos \theta }{2z}. \end{equation*}$$

(2) The optical path of the wavelet from the center.

$$\begin{equation*} L_{0s} =\frac {z}{\cos \theta }. \end{equation*}$$

(3) The optical path difference.

$$\begin{equation*} \Delta _{s} =L_{s} -L_{0s} =\frac {a^{2}\cos \theta }{2z} . \end{equation*}$$

The derivation implies that the optical path differences in the meridian plane and the sagittal surface are equal and are given as $\Delta =a^{2}\cos \theta /2z$; the off-axis Fresnel number can be expressed as

$$\begin{equation*} N=N_{st} \ast \cos \theta . \end{equation*}$$

The equivalence of the optical path differences suggests that the diffraction patterns are the same in the horizontal and vertical directions.

Figure 3. The diffraction patterns obtained by the R–S (upper panel) and analytical (lower panel) formulas.

3.2. Numerical calculation

The Rayleigh–Sommerfeld (R–S) nonparaxial diffraction integral is adopted to handle beams under oblique incidence; some approximations are introduced to avoid complicated calculations. A simple analytical formula for the nonparaxial intensity distribution is derived to reduce the computational complexity.

3.2.1. Nonparaxial intensity diffraction behind a circular aperture

The obliquely incident beam is no longer paraxial; hence, the R–S formula is used to calculate the distribution of the diffracted field^{[13, 14]}. The coordinate system is selected as shown in Figure 1.

(2)$$\begin{eqnarray} E(x,y,z)&=&\frac {1}{j\lambda }\int \int E_{1} (x_{1} ,y_{1} ,0) \frac {\exp (jkR)}{R} \nonumber \\ &&\times \,\biggl (1+\frac {j}{kR}\biggr )\frac {z}{R}dx_{1} dy_{1}, \nonumber \\ R&=& [(x-x_{1} )^{2}+ (y-y_{1})^{2}+z^{2}]^{\frac {1}{2}} , \label {eq1} \end{eqnarray}$$

where $a$ is the radius of the circular aperture, $z$ is the distance from the diffraction screen to the observation screen, $R$ denotes the distance from the source point $(x_{1} ,y_{1} ,0 )$ to the field point $(x,y,z)$, and $E_{1} (x_{1} ,y_{1} ,0 )=\exp [jk (a+y_{1} )\sin \theta ]$ is the amplitude distribution of the incident field.

Although the R–S formula can accurately calculate the nonparaxial scalar diffraction field and yield an accurate off-axis Fresnel number, it is difficult to obtain a universal expression for this number because of the complexity of the mathematical and numerical calculations. Thus, it is necessary to adopt an effective approximation to obtain a concise expression for the off-axis Fresnel number.$R$ is expanded into a Taylor series around $L$^[15]:

(3)$$\begin{eqnarray} R&=&[(x-x_{1})^{2}+ (y-y_{1})^{2}+z^{2}]^{\frac {1}{2}} \nonumber \\ &\approx & L+\frac {x_{1}^{2}-2xx_{1}}{2L}+\frac {y_{1}^{2}-2yy_{1} }{2L}, \label {eq2} \end{eqnarray}$$

where $L=\sqrt{x^{2}+y^{2}+z^{2}} $ is the distance along the auxiliary axis and $L^{2}\gg (x_{1}^{2}+y_{1}^{2}-2xx_{1}-2yy_{1} )_{\max }$.

The circular function is expressed as a series expansion with a complex Gaussian function^[16]

$$\begin{equation*} \mathit {circ}\biggl (\frac {\sqrt {x_{1}^{2}+y_{1}^{2}}}{a^{2}}\biggr )= \sum _{N=1}^{10} A_{N} \exp \biggl (-B_{N} \frac {x_{1}^{2}+y_{1}^{2}}{a^{2}} \biggr ) , \end{equation*}$$

where $A_{N}$ and $B_{N}$ are the expansion coefficients.

Using the expression into Equation (2) yields

(4)$$\begin{eqnarray} &&E(x,y,z) = \frac {\pi \cos ^{2}\theta }{j\lambda z}\exp \biggl [jk \biggl (\frac {z}{\cos \theta }+a\sin \theta \biggr ) \biggr ] \nonumber \\ &&\quad \times \,\sum _{N=1}^{10} \frac {A_{N}}{B_{N}/a^{2}-jk\cos \theta /2z} \nonumber \\ &&\quad \times \, \exp \biggl \{ \frac {(jk\cos \theta /z)^{2}[x^{2}+(y-z\tan \theta )^{2}]} {4 (B_{N}/a^{2}-jk\cos \theta /2z)}\biggr \} . \label {eqn4} \end{eqnarray}$$

The coordinates of the focal point $C$ are expressed as $x_{0} =0,y_{0} =z\tan \theta $; substitution this expression into Equation (4) gives the complex amplitude distribution of the focal point $C$,

(5)$$\begin{eqnarray} E(x_{0} ,y_{0} ,z)&=&\frac {\pi \cos ^{2}\theta }{j\lambda z}\exp \biggl [jk\biggl (\frac {z}{\cos \theta }+a\sin \theta \biggr ) \biggr ] \nonumber \\ &&\times \,\sum _{N=1}^{10} \frac {A_{N}}{B_{N}/a^{2}-jk\cos \theta /2z} . \end{eqnarray}$$

The intensity of the focal point on the auxiliary axis is given as

(6)$$\begin{equation} \label {eq3} I(x_{0} ,y_{0} ,z )=E (x_{0} ,y_{0} ,z )\cdot E^{\ast } (x_{0} ,y_{0} ,z ). \end{equation}$$

3.2.2. In silico simulations

(1) Comparison with the diffraction pattern.

Taking $a=0.5\ {\rm mm}$, $\lambda =632.8\ {\rm nm}$, $z=93\ {\rm mm}$, $\theta =20^{\circ }$, the diffracted patterns (Figure 3) are simulated by using Equations (2) and (4); the analytical formula significantly reduces the numerical complexity effort because of the analytical treatment.

Both patterns are roughly similar; however, a difference still exists because the analytical formula is derived under approximation conditions. The diffraction pattern obtained by the R–S formula is not circular; the radial intensity distributions are different in the horizontal and vertical directions. The diffraction pattern obtained using the analytical formula exhibits the same intensity distribution in both directions; the patterns are coincident with those obtained in Section 3.1, in which the optical path differences are approximately equal in both directions. However, the focal point extrema using the two methods are consistent, which indicates the validity of the analytical formula in calculating the off-axis Fresnel number.

(2) Off-axis Fresnel number derived through numerical calculations.

From the definition of the equivalent off-axis Fresnel number, $I\mbox{--}z$ and $N\mbox{--}z$ curves are acquired from analytical calculations. Figure 4 compares the curves under normal and oblique incidence; the result implies that the position $z$ of the intensity extrema under oblique incidence exhibits an offset to the left relative to the normally incident one. This offset is attributed to $L$, which is taken as the auxiliary axis by employing an axis transformation in the off-axis case (Figure 1). If the axial distance between the extreme values is defined as the diffractive period, the period becomes shorter when a beam is obliquely incident (Figure 4(a)).

Figure 4. $I\mbox{--}z$ (a) and $N\mbox{--}z$ (b) curves.

The simple analytical formula is used to calculate the off-axis Fresnel number. Based on the standard Fresnel number, the off-axis Fresnel number is expressed as $N=N_{st} \ast C_{1} $, where $C_{1} $ is the correction factor. Through curve fitting, the correction factors under different incident angles are obtained from the simulation. The solid line in Figure 5 represents the curve of $C_{1} $, and the dots represent the value of $\cos \theta $; $C_{1} $ is substantially equal to $\cos \theta $.

The off-axis Fresnel number can be expressed as

(7)$$\begin{equation} \label {eq4} N=N_{st} \ast \cos \theta . \end{equation}$$

The same expression is obtained in Section 3.1. Comparison of the expression with the standard Fresnel number yields an equivalent propagation distance $z_{\mathit{eff}} =z/\cos \theta $ under oblique incidence. This parameter is the propagation distance along the auxiliary axis $L$. When $\theta $ approaches zero, Equation (7) becomes $N=a^{2}/\lambda z$, the normally incident Fresnel number.

Figure 5. Curve of $C_{1}$.

3.3. Scope of application

The off-axis Fresnel number is established under certain approximations. Hence, the ratio of the propagation distance and radius has to meet specific conditions. The accuracy of the Fresnel number obtained by the R–S formula allows comparison of the $N\mbox{--}z$ curves derived from the R–S and analytic formulas, which gives the scope of application of the expression. Figure 6 illustrates the $N\mbox{--}z$ curves under different incident angles and upon setting $a=0.5\ {\rm mm}$, $\lambda =632.8\ {\rm nm}$.

Figure 6. $N\mbox{--}z$ curves under different incident angles.

The curves agree with each other well for $N\le 8$; the expression derived in this paper is established for a relatively fine beam. When the propagation distance $z$ is small with respect to the radius $a$, the R–S formula and numerical calculation are used to determine the Fresnel number. In laser systems, $z$ is usually much larger than $a$; therefore the expression is generally applicable.

4. Further improvement

The correction factors $C_{1} $ and $C_{2} $ are introduced into the definition of the Fresnel number in Equation (1). The expression for $C_{1} $ is acquired as $C_{1} =\cos \theta $, which implies consistency between normal and oblique incidences in the diffractive process; the two incidences can be unified by axis transformation.

Figure 7. Diagram of an obliquely incident spherical wave.

To further explore the correction factor $C_{2} $ under oblique incidence, an obliquely incident spherical wave is selected with a curvature center at point $S$ and a curvature radius of $R_{c} $ (Figure 7). The optical path difference is calculated between the wavelet from the edge and the wavelet from the center to the focal point C, in both the meridian and sagittal planes; the difference remains equal:

$$\begin{equation*} \Delta =\frac {a^{2}\cos \theta }{2\lambda }+\frac {a^{2}}{2R_{c} }. \end{equation*}$$

The equivalence of the optical path differences yields the off-axis Fresnel number for an incident spherical wave:

(8)$$\begin{equation} \label {eq5} N=\frac {a^{2}\cos \theta }{\lambda z}+\frac {a^{2}}{\lambda R_{c} }. \end{equation}$$

The correction factor $C_{2} =a^{2}/\lambda R_{c} $ is identical to the factor under normal incidence, indicating that the factor is not related to the incident angle, but is determined by the curvature radius of the incident wavefront; this result proves the correctness of the off-axis Fresnel number. In the propagation process, the effect of the wavefront on the optical path is not related to the incident angle.

Equation (8) reveals that the Fresnel number $N$ is related to $a,z,R_{c} $ and $\theta $, which explains the function of the off-axis optical system in the design of laser systems. Adjustment of $\theta $ by oblique incidence or tilted optical elements improves the radial intensity distribution, which reduces the harm to optical elements caused by vibration generated by diffraction.

The off-axis Fresnel number is also applicable for non-circular apertures and complex optical systems. For a non-circular aperture, $C_{2} $ is independent of the incident angle; this value is a function of the aperture shape. Hence, $C_{2} $ is similar to the correction factor under normal incidence^[3]. $C_{2} $ is equal to 0.23 from our results for a square aperture (which is almost the same as the factor in Ref. [7]). In complex optical systems, the optical path difference can be solved by adopting matrix optics along the auxiliary axis $L$. The essence is the axis transformation in off-axis optical systems.

5. Conclusions

The off-axis Fresnel number is defined in this paper: $N=(a^{2} /\lambda z )\ast C_{1} +C_{2} $. Theoretical analysis and numerical calculation yield $C_{1} =\cos \theta $; $C_{2} $ is independent of the incident angle, but dependent on the incident wavefront and the aperture shape. In summary, the following conclusions are reached. (1) During propagation, normal and oblique incidences are consistent and can be unified by the axis transformation factor $C_{1} =\cos \theta $. (2) The Fresnel number can be utilized to prove that the effects of the incident wavefront and the aperture shape are not related to the incident angle $\theta $. (3) The Fresnel number has a significant function in the design of laser systems, such as the effect of off-axis optical systems. Change of $\theta $ by oblique incidence or tilted optical elements improves the radial intensity distribution. This improvement reduces harm to optical elements, which is caused by diffraction-generated vibrations.

The Fresnel number is no longer confined to normal incidence; the number can be used to explain more diffractive optical phenomena, such as the design of off-axis laser systems. The expression is also suitable for incident waves of arbitrary shape, non-circular diffractive apertures and complex optical systems.