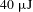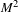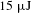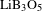High pulse energy fiber/solid-slab hybrid picosecond pulse system for material processing on polycrystalline diamonds

Abstract

We demonstrate an all polarization-maintaining (PM) fiber mode-locked laser seeded, hybrid fiber/solid-slab picosecond pulse laser system which outputs $40~\unicode[STIX]{x03BC}\text{J}$, 10 ps pulses at the central wavelength of 1064  nm. The beam quality factors $M^{2}$ in the unstable and stable directions are 1.35 and 1.31, respectively. $15~\unicode[STIX]{x03BC}\text{J}$ picosecond pulses at the central wavelength of 355 nm are generated through third harmonic generation (THG) by using two $\text{LiB}_{3}\text{O}_{5}$ (LBO) crystals, in order to get better processing efficiency on polycrystalline diamonds. The high pulse energy and beam quality of these ultraviolet (UV) picosecond pulses are confirmed by latter experiments of material processing on polycrystalline diamonds. This scheme which combines the advantages of the all PM fiber mode-locked laser and the solid-slab amplifier enables compact, robust and chirped pulse amplification-free amplification with high power picosecond pulses.

1 Introduction

High power, high repetition rate pulse lasers with near-diffraction-limited beam quality have made significant contributions in many applications such as X-ray generation^[1], attosecond pulses generation^[2] and material processing^[3–7]. In particular, the performance of material precise processing varies largely due to different pulse durations. Generally, with the decreasing of pulse duration, the material processing results become better^[3]. It can be explained that with the ultrashort pulse duration (i.e., less than one picosecond), laser pulse transfers almost all of its energy to the electrons, rather than the atoms/lattice, and the pulse is shorter than the time takes for the energy of the electronics to reach equilibrium with the lattice, whereas the pulse machining by nanosecond or longer pulse laser may involve a solid-state phase transformation, melting or evaporation of the target due to thermal activation^[4]. Although $Q$ -switch laser processing systems have achieved great successes for their simple and stable schemes, the processing quality and scope of applications are limited, due to nanosecond pulse durations^[4–7].

All polarization-maintaining (PM) fiber mode-locked lasers have been confirmed as robust, compact and alignment-free light sources with the output pulse duration of less than 10 ps^[8–13]. Particularly, in most schemes of these kinds of mode-locked lasers, the mode-locking is achieved by passive mode-locked devices such as carbon nanotube (CNT) or semiconductor saturable absorber mirror (SESAM), which have simpler mode-locking mechanism than traditional nonlinear polarization rotation (NLPR) mode-locked lasers. On the other hand, due to the fact that lights are always trapped in the PM fiber without any free space optical devices, these structures are less sensitive to external temperature and stress perturbations. As a result, this kind of mode-locked laser shows much more robustness and less output states, compared to traditional NLPR mode-locked lasers, which is an ideal alternative to $Q$ -switch laser in material processing applications.

Another problem is how to amplify the seed pulse up to desired output pulse energies. Unlike the regenerative amplifier scheme which is hard to stay stable at high repetition rate^[14], the master-oscillator power amplifier (MOPA) configuration has been widely used in seed pulse amplification at higher repetition rate. However, for fiber-based amplifiers, because the small mode areas and long interaction lengths for light propagating in optical fiber will cause pulse distortions and pulse break-up, complex chirped pulse amplification (CPA) configuration must be set up in most cases^[15–19], which will increase the complexity of systems. Recently, the partially pumped slab laser systems have been widely studied, due to the ability of circumventing nonlinearity by the short reaction distance between the light and gain matter^[20–27]. These slab laser systems have provided a novel approach to realize CPA-free amplification with high power ultrafast pulses. Indeed, these slab crystal amplifiers also have some disadvantages. For example, the slab amplifiers need bulk cooling systems for avoiding beam quality degradation induced by the thermal effects. Besides, the slab amplifiers require unique imaging systems for laser amplification, which will make it more difficulty in system adjustment. Despite these shortcomings, these slab crystal amplifiers are still attractive because they promise a compact and robust scheme for high power pulse amplification without complex CPA technique. However, in all these slab laser systems, the seed pulses are produced from solid-state mode-locked/ $Q$ -switch oscillators. Compared with the turn-key all-fiber mode-locked oscillators, these solid-state oscillators are less compact, less robust and harder to build, which make it bulky, costly and far from real-world applications.

Figure 1. Setup of the all PM fiber mode-locked laser. ISO: isolator, WDM: wavelength division multiplexer, SESAM: semiconductor saturable absorber mirror, FBG: fiber Bragg grating, PD: photonics detector, SG: signal generator, AOM: acoustic optical modulator, RF signal: radio frequency signal.

Here, we first demonstrate an all PM fiber mode-locked laser seeded, hybrid fiber/solid-slab picosecond pulse laser system. The MOPA design is used in this system. Due to the all PM fiber structure of the pulse seed source, the whole laser system becomes much more compact and stable. By establishing a suitable design, we achieve $40~\unicode[STIX]{x03BC}\text{J}$ , 10 ps pulses output at the central wavelength of 1064 nm. The beam quality factors $M^{2}$ in the unstable and stable directions are 1.35 and 1.31, respectively. In order to get better processing efficiency for materials which have low absorption in infrared radiation such as the diamonds^[28], $15~\unicode[STIX]{x03BC}\text{J}$ picosecond pulses at the central wavelength of 355 nm are generated through third harmonic generation (THG) by using two $\text{LiB}_{3}\text{O}_{5}$ (LBO) crystals. Thanks to the high pulse energy and beam quality of these ultraviolet (UV) picosecond pulses, we achieve a high performance of material processing on polycrystalline diamonds in the latter experiments.

2 Experimental setup

Our experimental setup includes three main parts: the all PM fiber mode-locked laser, slab laser amplifier and ultraviolet generator.

2.1 All PM fiber mode-locked laser

The all PM fiber mode-locked laser contains a passively mode-locked oscillator, a fiber pre-amplifier and a fiber-based pulse picker (shown in Figure 1). The laser oscillator is based on a Fabry–Perot (FP) cavity configuration. The total cavity length is about 3.3 m, which consists of a piece of 100 cm PM Yb-doped gain fiber (Nufern, PM-YSF-6/125-HI), pumped by a 976 nm power laser diode (LD) via a PM wavelength division multiplexer (WDM). A SESAM directly butt-coupled to the PM fiber is used as one end reflector of the FP cavity for self-started passive mode-locking of the fiber laser. It has a modulation depth of 31%, a relaxation time of 4 ps and a saturation fluence of $40~\unicode[STIX]{x03BC}\text{J}/\text{cm}^{2}$ (Batop, SAM-1064-57-4ps). A PM fiber Bragg grating (FBG) is used as one reflector of the FP cavity, and the FBG has a reflection peak wavelength of 1063.9 nm with $-3$  dB bandwidth of 0.5 nm, which is designed to match the gain spectrum of Nd: $\text{YVO}_{4}$ crystal. It is worth noting that this FBG is also optimized for low noise operation^[13]. The laser consists of a total PM fiber length of ${\sim}3.3~\text{m}$ , which results in a laser repetition rate of ${\sim}30~\text{MHz}$ . The mode-locked pulses are directed out by a 50 : 50 optical PM coupler. After outputting from the oscillator laser, 10% of the laser is directed out by a 90 : 10 optical PM coupler for producing a delayed gate signal for latter pulse picking. The remaining 90% of the laser is coupled into the PM fiber laser pre-amplifier, which consists of a PM WDM, a 1.2 m PM Yb-doped gain fiber (the same type as used in the oscillator laser) and a 976 nm power LD. A fiber isolator (ISO) is installed between the seed laser and the pre-amplifier to isolate the returning light. The pulse picker used in our experiment consists of three components, including a photonics detector (PD, Thorlabs, PDA36A), a signal generator (SG, SRS, DG645) and a fiber-based acoustic optical modulator (AOM, AA Opto-Electronic, MT250-IR6-Fio-PM0). Irradiated by the 10% seed pulses, the PD generates a synchronous radio frequency (RF) signal which is equal to the repetition rate of the seed pulses. Triggered by this RF signal, the SG could produce a delay gate signal with a lower frequency which can be an integral fraction of the repetition rate. Then this delay gate signal will be sent to the AOM as the trigger signal for pulse picking. As a consequence, the repetition rate of the picked pulses could be adjusted by setting the SG. At last the picked pulses are collimated by a fiber collimator.

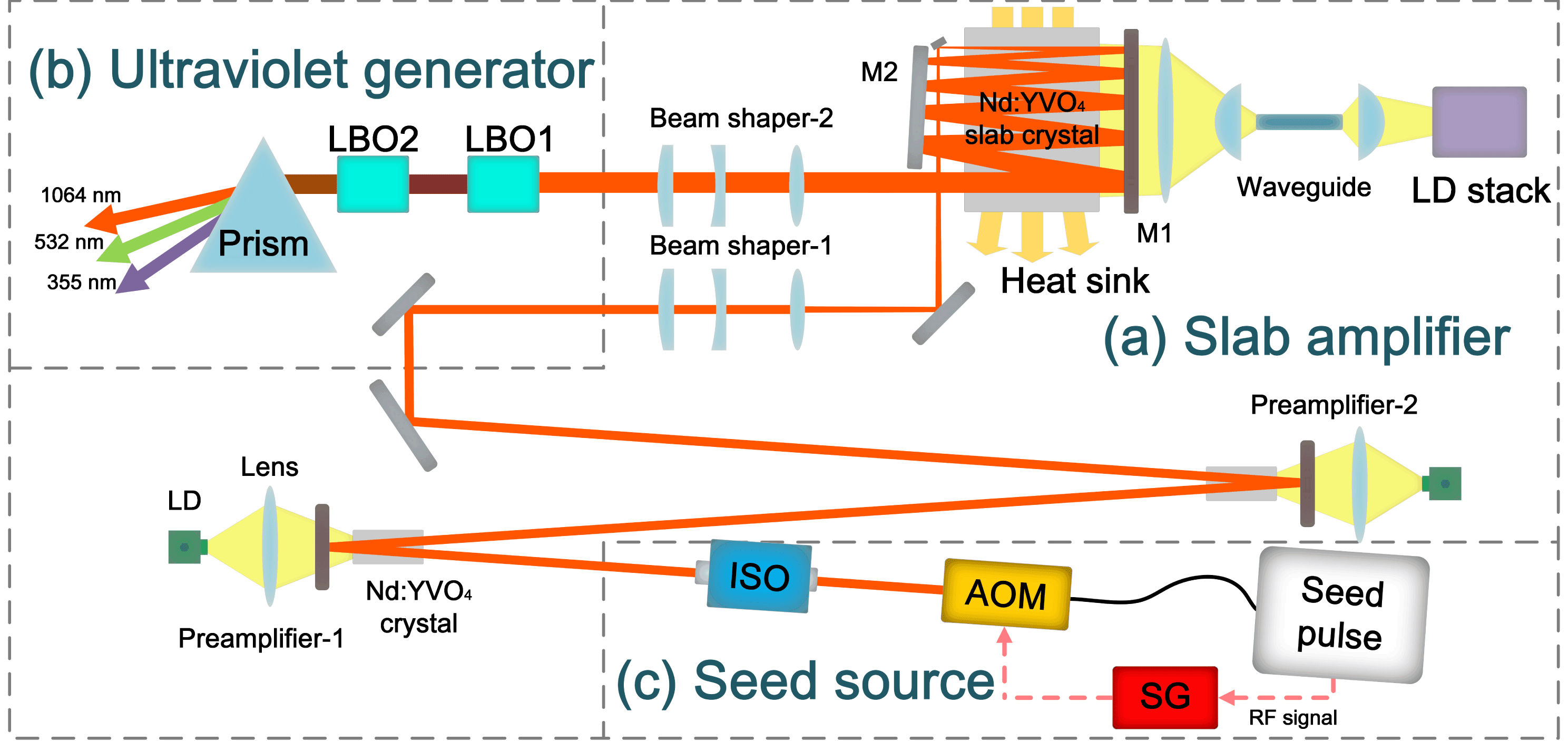
Figure 2. Configuration of the ultraviolet picosecond pulse laser system.

2.2 Slab laser amplifier and ultraviolet generator

Due to the fact that the Nd: $\text{YVO}_{4}$ crystal has a large emission cross-section and polarized emission attributed to its natural birefringence, we choose it as the gain medium in latter solid-state amplification stages. Besides, the Nd: $\text{YVO}_{4}$ crystal also shows much more price advantages over the Yb-based crystal and enough gain bandwidth for ${\sim}10~\text{ps}$ pulse amplification as well. The structure of solid-state slab laser amplifier is shown in Figure 2(a). In order to compensate the energy loss by the former pulse picker, two end-pumped double-pass Nd: $\text{YVO}_{4}$ pre-amplifiers are employed for energy amplification before the slab amplifier. An optical isolator is used to protect the all PM fiber mode-locked laser against returning light from these two amplifiers. The slab amplifier mainly consists of a LD stack, two beam shapers, a pair of plane mirrors and an Nd: $\text{YVO}_{4}$ slab crystal. The LD stack emits pump light at center wavelength of 808 nm and the beam is shaped by a coupling system which consists of a planar waveguide, a spherical lens and several cylindrical lenses. Through the coupling system, a $14~\text{mm}\times 1~\text{mm}$ homogeneous pump line is measured on the pump end of the slab Nd: $\text{YVO}_{4}$ crystal, which is nearly Gaussian distribution in the vertical direction and homogeneous in the horizontal direction. A 0.3% doped Nd: $\text{YVO}_{4}$ crystal is used as the gain medium of the slab amplifier. The crystal has a dimension of $10~\text{mm}\times 14~\text{mm}\times 1~\text{mm}$ . The two large faces ( $10~\text{mm}\times 14~\text{mm}$ ) of the slab crystal are contacted by two heat sinks, which are cooled by circulating water at the temperature of $25\,^{\circ }\text{C}$ . The two transmitting faces ( $14~\text{mm}\times 1~\text{mm}$ ) are antireflective coated. There are two types of mirrors in our system. M1 is the dichroic mirror which has high transmission at 808 nm and high reflection at 1064 nm. M2 has high reflection at 1064 nm.

Before coupling into the slab amplifier, the seed beam is shaped by beam shaper-1 which consists of two cylindrical lenses and a spherical lens. In the horizontal direction, the beam shaper-1 is used to compress the seed beam to be line-like for mode matching between the seed beam and the pump light. In the vertical direction, the spherical lens is used to focus the seed beam (which is Gaussian distribution). Meanwhile the spherical lens increases the divergence angle of the seed beam. As a result, the beam diameter will be wider for every passage through the crystal which ensures that the optical power density is always similar. The beam shaper-2 is used to restore the amplified laser beam to Gaussian distribution in both the horizontal and vertical directions.

The ultraviolet generator shown in Figure 2(b) consists of two commercial LBO crystals without additional heating. In LBO1, the 532 nm pulses are generated from 1064 nm pulses of the slab amplifier by doubling-frequency generation (DFG). The 355 nm pulses are produced in LBO2 from 532 nm and 1064 nm pulses, through sum frequency generation (SFG). A prism is used to separate 355 nm, 532 nm and 1064 nm pulses.

The output spectra of the all PM fiber mode-locked laser are recorded by an optical spectrum analyzer (Yokogawa-AQ6370B) with the resolution of 0.02 nm. Its RF spectrum is measured by a high speed photo-detector (Thorlabs DET10A/M) which is connected to an oscilloscope (Iwatsu, 400 MHz). The pulse duration is measured by an optical autocorrelator (APE, PulseCheck).

Figure 3. Output characteristics of the all PM fiber pulse seed source. (a) Spectrum profiles, the inset shows the long term stability of the seed pulses (in the 10% output port) in 2 h. (b) Autocorrelation trace and its Gaussian fitting.

3 Experimental results and discussions

When the pump power is 75 mW, the oscillator laser is self-started mode-locking with the output power of 2 mW. As the pump power increases to 130 mW, 5 mW output power is achieved. Then the output power is amplified to 75 mW with 400 mW pump power of the fiber pre-amplifier. Thanks to the all-fiber construction, we realize a low repetition rate of 30.7 MHz with a compact size, which is difficult to a solid-state mode-locking laser. The fiber-based pulse picker reduces the repetition rate to 500 kHz with diffraction efficiency of ${\sim}50\%$ , according to the output power of 0.6 mW. Figure 3(a) shows the output optical spectrum profiles of the oscillator, pre-amplifier and pulse picker. Due to the normal dispersion and self-phase modulation (SPM) effect in the pre-amplifier and pulse picker, the full width at half-maximum (FWHM) spectral width is broadened to ${\sim}0.75~\text{nm}$ , which is acceptable for the Nd: $\text{YVO}_{4}$ amplifier. Figure 3(b) shows the autocorrelation (AC) trace. The black solid line represents our experimental data, and the red dotted line is its Gaussian fitting. The FWHM duration of the fitted curve in Figure 3(b) is $1.414\times 9.09~\text{ps}$ . In addition, the stability of mode-locking can be greatly improved by using all PM fiber construction, as shown in Figure 1. In our experiment, the mode-locking state e.g., the spectrum profile would not be affected by slight mechanical stress and air-wobbling because of the insensitivity of the PM fiber to external perturbations, which is an accepted advantage of the mode-locked laser with all PM fiber format. Besides, because the stability of amplified pulses significantly follows from the stability of seed pulses, we measure the output powers of the seed pulses (in the 10% output port), at the frequency of 1 time per second in a long time of 2 h. We plot the measured data in the inset of Figure 3(a) and the calculated root mean square (RMS) power fluctuations are only ${\sim}0.12\%$ . We believe that the seed fiber laser with this high stability will be beneficial to a robust and stable laser system.

Figure 4. Output characteristics of the all slab amplifier. (a) Measured (dots) and calculated (line) output power of the slab amplifier. (b) Long term stability of the slab amplifier in 2 h. (c) Beam radius and profile. (d) Autocorrelation trace and its Gaussian fitting.

The seed beam is amplified to ${\sim}90~\text{mW}$ by two end-pumped double-pass Nd: $\text{YVO}_{4}$ pre-amplifiers. In our design, the seed beam will pass through the slab crystal 10 times. At the pump power of 125 W emitted by the LD stack, the output power of the slab amplifier is 3.5 W. As the pump power increases up to 260 W, 19.8 W output power is achieved. The corresponding pulse energy is about $40~\unicode[STIX]{x03BC}\text{J}$ , at the repetition rate of 500 kHz. Figure 4(a) shows the measured (dots) and calculated (line) output power. The slope efficiency is ${\sim}12\%$ . This low slope efficiency is due to the low output power of the seed beam. However, the corresponding single-pass amplification factor is about 1.71, which is in line with the general performance of the slab amplifier. With a more powerful seed beam ( ${>}1~\text{W}$ ), the output power and the extraction efficiency can be further improved. This high power seed beam can be achieved by optimizing the pre-amplifiers or cascading more amplifiers. We also measure the output powers of the slab amplifier in 2 h. The measured data is shown in Figure 4(b), and the corresponding RMS power fluctuations are only ${\sim}0.94\%$ . It is evident that this high stability from the whole system benefits from the stable and robust all PM mode-locked fiber laser. Figure 4(c) shows the standard position-beam-radius measurements by a laser beam profiler, which indicates that beam quality is $M_{x}^{2}=1.35$ or $M_{y}^{2}=1.31$ in the orthogonal directions. Better beam quality makes it easier to focus the laser beam to a smaller point for higher optical power density, which is significant in material processing systems. The measured autocorrelation trace of the slab amplifier output is shown in Figure 4(d). The FWHM of the pulse duration is 10.89 ps (by Gaussian fitting), which is a bit wider than the seed pulse. Because the negligible dispersion induced by the small slab crystal cannot broaden these narrowband picosecond pulses with the variational duration as large as ${\sim}1.8~\text{ps}$ , and the Nd: $\text{YVO}_{4}$ crystal only provides ${\sim}1~\text{nm}$ gain bandwidth at 1064 nm (comparable to the seed pulse after pulse picker), we attribute this temporal broadening to slight spectral mismatch and the finite gain bandwidth of Nd: $\text{YVO}_{4}$ crystal. Then the amplified picosecond pulses are coupled in the ultraviolet generator without focusing. The ultraviolet generator outputs 7.5 W UV pulses at the central wavelength of 355 nm. The optical–optical efficiency and the corresponding pulse energy are 37.5% and $15~\unicode[STIX]{x03BC}\text{J}$ , respectively. By assuming that the pulse duration is 10 ps, the peak power reaches 1.5 MW.

In order to test this laser system, we carry out an experiment of material processing on polycrystalline diamond samples. The material processing by picosecond pulses can be generally considered as strong evaporation, the critical condition for evaporation can be written as^[3]

(1) $$\begin{eqnarray}\displaystyle F_{A} & = & \displaystyle \frac{4P_{0}}{\unicode[STIX]{x1D70B}t_{0}f_{r}d^{2}}\geqslant F_{th}e^{\unicode[STIX]{x1D6FC}z},\end{eqnarray}$$

(2) $$\begin{eqnarray}\displaystyle F_{th} & = & \displaystyle \unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FC},\end{eqnarray}$$

where $F_{A}$ is the power density of a single laser pulse, $P_{0}$ is the average power output, $t_{0}$ is the pulse width, $f_{r}$ is the repetition rate, $d$ is focused spot diameter, $\unicode[STIX]{x1D6FC}$ is the wavelength-related material absorption coefficient and $z$ is the direction perpendicular to the target surface. $F_{th}$ is the threshold laser fluence for evaporation, which is determined by the density $\unicode[STIX]{x1D70C}$ and the specific (per unit mass) heat of evaporation  $\unicode[STIX]{x1D714}$ .

Figure 5. SEM images of laser-cut grooves on the diamond surface by 355 nm picosecond pulses with (a) $P_{0}=1~\text{W}$ at the repetition rate of 500 kHz (the corresponding pulse energy is $2~\unicode[STIX]{x03BC}\text{J}$ ) and (b) $P_{0}=1~\text{W}$ at the repetition rate of 10 MHz (the corresponding pulse energy is $0.1~\unicode[STIX]{x03BC}\text{J}$ ), respectively.

According to Equation (1), we need to increase the power density up to the threshold laser fluence for evaporation, in order to achieve a high processing performance. Thanks to the high output beam quality, the UV picosecond beam can be focused to $d=10~\unicode[STIX]{x03BC}\text{m}$ by a lens with the focal length of 40 mm. The polycrystalline diamond samples are irradiated normal to the target surface in open air and scanned at a rate of $600~\text{mm}/\text{s}$ by moving a motorized stage during laser irradiation. For comparison, the repetition rate $f_{r}$ of the UV beam is set to be 500 kHz or 10 MHz, with the same average power $P_{0}=1~\text{W}$ . The scanning electron microscope (SEM) observations (shown in Figure 5(a)) show that the former processing result is satisfactory both in efficiency and quality. Meanwhile with the similar average power but the much lower pulse energy, the latter processing result is unsatisfactory, for both the rough surface and the narrow width of the laser-cut grooves, as shown in Figure 5(b). This can be explained that with $f_{r}=500~\text{kHz}$ (the pulse energy is 20 times higher than $f_{r}=10~\text{MHz}$ ) the pulse power density is high enough to realize evaporation process in the entire area irradiated by the focal spot. As a result, the width of the laser-cut grooves is similar to the diameter of the focal spot. In contrast, the width of the laser-cut grooves is much shorter than the diameter of the focal spot, with $f_{r}=10~\text{MHz}$ .

4 Conclusions

In conclusion, we demonstrate an all PM fiber mode-locked laser seeded, hybrid fiber/solid-slab picosecond pulse laser system without using CPA technology. The all PM fiber mode-locked laser is operated at the central wavelength of 1064 nm, and outputs 75 mW, 9.09 ps at a low repetition rate of 30.7 MHz. After the decreasing of repetition rate (i.e., down to 500 kHz) by a fiber-based pulse picker and then energy amplification by two end-pumped double-pass Nd: $\text{YVO}_{4}$ pre-amplifiers, the pulse energy is amplified to $40~\unicode[STIX]{x03BC}\text{J}$ by a partially pumped slab Nd: $\text{YVO}_{4}$ amplifier. The beam quality factors $M^{2}$ in the unstable and stable directions are 1.35 and 1.31, respectively. The pulse duration is broaden to 10.89 ps due to finite gain bandwidth of the slab Nd: $\text{YVO}_{4}$ crystal. $15~\unicode[STIX]{x03BC}\text{J}$ picosecond UV pulses at 355 nm are achieved through THG from two commercial LBO crystals. We use these UV picosecond pulses to process polycrystalline diamond samples and experimental results show that the high performance benefits from the high pulse energy and beam quality. This compact, robust and cost-effective UV picosecond pulse system is likely to benefit a number of material processing applications.