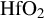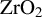Exploring fs-laser irradiation damage subthreshold behavior of dielectric mirrors via electrical measurements

Abstract

With ultrafast laser systems reaching presently 10 PW peak power or operating at high repetition rates, research towards ensuring the long-term, trouble-free performance of all laser-exposed optical components is critical. Our work is focused on providing insight into the optical material behavior at fluences below the standardized laser-induced damage threshold (LIDT) value by implementing a simultaneous dual analysis of surface emitted particles using a Langmuir probe (LP) and the target current (TC). ${\mathrm{HfO}}_2$ and ${\mathrm{ZrO}}_2$ thin films deposited on fused silica substrates by pulsed laser deposition at various ${\mathrm{O}}_2$ pressures for defect and stoichiometry control were irradiated by Gaussian, ultrashort laser pulses (800 nm, 10 Hz, 70 fs) in a wide range of fluences. Both TC and LP collected signals were in good agreement with the existing theoretical description of laser–matter interaction at an ultrashort time scale. Our approach for an in situ LIDT monitoring system provides measurable signals for below-threshold irradiation conditions that indicate the endurance limit of the optical surfaces in the single-shot energy scanning mode. The LIDT value extracted from the LP-TC system is in line with the multipulse statistical analysis done with ISO 21254-2:2011(E). The implementation of the LP and TC as on-shot diagnostic tools for optical components will have a significant impact on the reliability of next-generation ultrafast and high-power laser systems.

1. Introduction

The progress of modern high-power laser systems towards the generation of extreme fields, currently demonstrating up to 10 PW pulses^{[ 1, 2]}, has been impeded by one main challenge: the modest resistance to laser-induced optical damage of their constituent components. The threshold resistance is further stretched to the limits within post-compression techniques via thin film compression^{[ 3]}, which have been successfully used to increase the peak power for different input laser pulse duration^{[ 4, 5]} and J-level energy^{[ 6]}.

During multipulse fs-laser irradiation, there is a multitude of phenomena occurring in the optical coatings that are not completely understood. Thus, a generic term ‘incubation effect’ is often employed to account for all these effects^{[ 7, 8]} on the laser-induced damage threshold (LIDT). The appearance of the incubation effect lowers the LIDT value with the increase in the number of laser pulses. Besides the high cost of the destroyed optical component, catastrophic damage could create a plasma mirror on the surface of the affected optical component that might deflect the extremely powerful laser pulse in an unpredictable direction and cause additional extensive damage to other expensive equipment located in the vicinity. As shown in several studies^{[ 9– 11]}, the bandgap of the material is strongly connected to the measured LIDT value. However, the diffusion of the materials in multilayer coatings, together with the presence of the laser field, can lead to the presence of impurities in the optical coating material that introduces transient^{[ 12, 13]} or permanent midgap states that reduce the LIDT value of the components. For example, the presence of oxygen atom defects in ${\mathrm{HfO}}_2$ was studied in Ref. [14], while the laser-induced transient states were analyzed in Ref. [15] and attributed to the generation of excitons, bound electron–hole pairs, in the presence of the laser field.

The determination of the LIDT by irradiating the optical components with laser pulses and measuring the scattered light or the subsequent permanent modification of the surface morphology represents a standardized method^{[ 16]} to characterize the quality of these optical components. Alternative empiric methods to define the LIDT include piezoelectric transducers^{[ 17]}, white light generation^{[ 18]}, free-electron plasma luminosity^{[ 19]}, etc. However, the empirically determined LIDT of the optical components cannot be always completely reproduced on similar samples. This is the effect of minute modifications in the production processes at a microscopic scale that are not observed in the manufacturing process. Among these, residual contaminations of the material during preparation, polishing and substrate cleaning are other factors contributing to changes in the intrinsic properties of the material.

Over the years, numerous techniques have been developed for monitoring laser-ablated material. They often consider the fundamental mechanisms involved in short and ultrashort laser–matter interaction. The scenarios for material removal from the target follow a complex interconnectivity of electrostatic and thermal mechanisms, which are temporally and spatially separated: the first stages of laser ablation are of an electrostatic nature, while the second stages are of a thermal nature. In our previous work^{[ 20]}, we have shown that the Langmuir probe (LP) is a suitable technique for estimating the nanosecond ablation threshold limit as it detects contributions from each stage^{[ 21]}. Other reports focus on LP measurements of ablation threshold in the ns regime^{[ 22]}, while reports on the detection of the fs-incubation stage emphasize the necessity of having a minimum of 10,000 pulses to estimate the threshold^{[ 23]}. In general, the data available in the literature regarding LP measurements concerns the dynamics of the charged particle above the ablation threshold at a large distance (over 2–3 cm) from the target^{[ 24]}. However, as the LP technique is based on charge collection, it could be promising for subthreshold measurements. When relating to the LIDT, there is still key interest in the behavior of optical components below the LIDT where understanding electron emission and target compensation current in a wide range of irradiation conditions becomes imperative.

In this paper, we report on the determination of the LIDT on a series of ${\mathrm{HfO}}_2$ and ${\mathrm{ZrO}}_2$ thin films by implementing a novel approach based on the target current (TC) and LP method. The LP and the TC techniques are based on the collection of charges emitted from the thin film surface as a result of fs-laser irradiation. The LP and TC show a sensitivity improvement by a factor of 2 in the damage threshold measurements in single-pulse experiments, while still being in line with the statistical values offered by classical techniques. Comparisons are only made between dielectric thin films ( ${\mathrm{HfO}}_2$ and ${\mathrm{ZrO}}_2$ ) to avoid the field enhancement effects associated with multilayer dielectric coatings^{[ 25]}. The films are deposited by pulsed laser deposition in various conditions to correlate the stoichiometry of the film with its LIDT value.

2. Materials and methods

2.1. Thin film preparation

The pulse laser deposition (PLD) method was used to deposit a series of 70 nm thick ${\mathrm{HfO}}_2$ and ${\mathrm{ZrO}}_2$ thin films with different stoichiometries. An ArF excimer laser ( $\lambda$  = 193 nm, pulse duration $\tau$ = 25 ns) was focused on ${\mathrm{HfO}}_2$ and ${\mathrm{ZrO}}_2$ targets (Neyco, France) at a constant fluence of $2\;\mathrm{J}/{\mathrm{cm}}^2$ while 1 cm × 1 cm fused silica substrates (maintained at room temperature during the deposition) were placed at 4 cm from the target placed in the chamber. The metal-to-oxygen ratio in the films was controlled by adjusting oxygen pressures (0.6, 0.8 and 1 Pa). After deposition, the elemental composition and thickness of the films were determined using non-Rutherford backscattering spectrometry (NRBS) analysis with a collimated 3.042 MeV He ${}^{2+}$ beam, delivered by the 3.0 MV Cockcroft–Walton tandem accelerator at ‘Horia Hulubei’ National Institute for Physics and Nuclear Engineering (IFIN-HH), Măgurele, Romania^{[ 26, 27]}.

2.2. Methods

The experimental setup, as illustrated in Figure 1, comprises two main sub-assemblies^{[ 28]}. The first sub-assembly involves the measurement of the LP and TC in a vacuum, while the second sub-assembly is dedicated to in situ imaging in air.

Figure 1 Experimental setup. BS, beam splitter; EM, energy meter; FM, flip mirror; LASER, Ti:sapphire; L1 and L2, focusing lenses; LP, Langmuir probe; M1, high-reflection mirrors; M2, 99 $\%$ -reflection mirror; M3, spherical mirror; NDF, neutral density filter; OSC, oscilloscope; POL, polarizer; PD, photodiode; TC, target current; TS, translation stage; RS, rotation stage; VC, vacuum chamber; WP, half-waveplate. The inset illustrates the input beam profile used for A ${}_{\mathrm{eff}}$ calculation.

An AVESTA Ti:sapphire laser system was used to provide compressed laser pulses (70 fs, 800 nm, 10 Hz, 1.6 mJ, 8 mm diameter) to the experimental setup. The pulse energy was reduced by using the combination of a half-waveplate (WP) and a thin polarizer (POL). The measurements were performed using p-polarized laser pulses. The WP was mounted on a motorized rotation stage allowing the polarization change by up to 90° for 45° of WP rotation. The transmitted energy (3% root mean square (RMS)) was measured using a Gentec energy meter (EM) after each lens where the beam covered 70% of the detection area, while the photodiode (PD) can record a signal calibrated with the measured energy during shots. The laser pulses were focused by plano-convex lenses (L1, 40 cm focal length, and L2, 75 cm focal length) on the samples. The movement of the sample was assured by a 3D translation stage to cover multiple irradiation sites. The pulse duration (70 $\pm$ 3 fs) was measured using a SPIDER (spectral phase interferometry for direct electric-field reconstruction) device before the lenses.

The first assembly consists of a large Rayleigh range lens (L2) and a vacuum chamber (VC) where the sample, the rotation stage and the LP and TC measurement system were positioned. LP-TC experiments were performed inside a VC at a residual pressure of 10 ${}^{-3}$ Pa, in single-shot mode, on pristine surfaces. The oxide thin films were electrically connected to an oscilloscope for TC measurements, while a 2 mm long, 0.5 mm diameter tungsten wire was used as an active region for the LP, which was placed 1 cm away from the target. The LP was orthogonal with respect to the irradiated sample surface and off-axis with respect to the irradiation plane to avoid shadowing effects or potential interaction between the incoming beam and the LP. Both the LP floating current and TC were recorded by a Tektronix oscilloscope with a 50 Ω input impedance.

The second assembly, an imaging system (IS) (BS-M3-BS-Objective-CCD), was designed to efficiently monitor, in real-time, the intensity pattern in the interaction area (object plane) of a laser beam with the sample. The IS had a resolution of 13 μm (1 pixel = 1.7 μm), calibrated with a 1951 US Air Force (USAF) target. A variable neutral density filter (NDF) was implemented to adjust the amplitude of the image recorded by the charge-coupled device (CCD), in case of saturation.

The effective beam area on the target surface ( ${S}_{\mathrm{eff}}$ ) has been computed using Equation (1)^[29]:

(1) $$\begin{align}{S}_{\mathrm{eff}}={S}_{\mathrm{pixel}}\frac{\sum \limits_{\mathrm{pixel}}{A}_{\mathrm{pixel}}}{A_{\mathrm{max}}},\end{align}$$

where ${A}_{\mathrm{pixel}}$ and ${A}_{\mathrm{max}}$ indicate the amplitudes of each pixel in the CCD matrix and the maximum amplitude of the matrix, respectively. The pixel area ${S}_{\mathrm{pixel}}$ in the object plane of the IS is determined by calibration using a USAF 1951 target. Therefore, the threshold peak fluence was calculated as F ${}_{\mathrm{th}}$ =2E ${}_{\mathrm{th}}$ /A ${}_{\mathrm{eff}}$ , where E ${}_{\mathrm{th}}$ is the threshold energy at which the damage starts to occur^{[ 30]}.

Automation of the entire experiment requires a specific synchronization time control for all the devices. A delay generator triggered by a signal from the laser control unit is used to generate on-demand pulses by gating the opening of the Pockels cell and also to send synchronization signals to the camera, PD, NDF, stages and the oscilloscope used for data acquisition.

3. Results and discussion

The fundamental landscape of fs-laser–matter interaction is dominated by non-thermal and electrostatic interactions^{[ 31]}, mostly occurring on a sub-ps time scale. Therefore, key properties of the dielectric mirrors, such as defects and oxygen vacancies, can affect the local electrical property of the film and thus the local value of the LIDT. If we follow the fs-ablation scenario, which was reported by Bulgakova et al. ^{[ 32]}, the electrons are the first excited particles and will be ejected from the target, leaving behind a positively charged surface. The charge separation defines an electrical field that accelerates the target’s ions and leads to the subsequent breakdown of the materials. Since electron ejection is a gradual process, this means that even below the usual defined LIDT limit, charges can be collected by implementing electric diagnostics tools. Any charge imbalance in the sample as a result of the laser irradiation can be defined by two responses: a transient electronic current that will be collected by the LP and a compensation current in the dielectric film (target) with an opposite sign to maintain charge neutrality.

In Figure 2 we have plotted representative charge current traces collected by the probe (LP) and from the sample (TC) above and below the threshold according to optical measurements. The higher sensitivity of the TC is noticeable, as for a fluence of $1.2\;\mathrm{J}/{\mathrm{cm}}^2$ we observe that the LP is almost null or buried in the noise, while the TC is defined by a high rise time and quasi-exponential decrease described by a time constant of 2.84 $\times$ 10 ${}^{-4}$ s for ${\mathrm{HfO}}_2$ and 1.47 $\times$ 10 ${}^{-4}$ s for ${\mathrm{ZrO}}_2$ .

The TC defines charges with a low kinetic energy as defined by the lifetime of the signal. With the increase of the fluence and the passing of the LIDT ( $3.2\;\mathrm{J}/{\mathrm{cm}}^2$ ), the plasma forms. As a result of the laser–sample interaction, a positive ionic peak is seen with arrival time of less than 5 μs containing mostly metallic species followed by a negative contribution containing electrons and based on the shorter arrival time oxygen species, which are known to contribute to the negative peak of the floating LP current^{[ 33, 34]}. Above the LIDT, the TC is seen to increase with a factor of 3 for the ${\mathrm{ZrO}}_2$ and a factor of 6 for the ${\mathrm{HfO}}_2$ samples, with the time factors following a similar ratio. The implementation of the LP in tandem with the TC has also the role of understanding the removal mechanisms, as the LP can offer quantitative information about the ejected particles, which can be further correlated with the target compensation current temporal trace.

Figure 2 Transient currents recorded during fs irradiation of ${\mathrm{HfO}}_2$ (a) and ${\mathrm{ZrO}}_2$ (b) films.

Based on our data, the target compensation current is always significantly larger than the LP. The difference is understandable as the ionization degree for fs-laser-produced plasma is often low, with an important quantity of the ablated material being in the form of ionized fragments, clusters and nanoparticles. This contribution to the LP signal is difficult to differentiate due to the physical limitations of the diagnostics method. Also, while the LP collects the charges from a rather small solid angle of the irradiated surface, the TC collects the total target compensation charge. The results are in line with the reports^{[ 35]} where the breakdown of the graphite sample and the gentle ablation mechanism were discussed. This mechanism is characteristic of the low fluence regime and is defined by the breakdown of the sample into larger components with a low degree of ionization.

Further analysis of the ablated ion and electronic cloud in the above LIDT fluence range is performed by implementing the approach reported in Ref. [36] and treating the time of arrival in a shifted Maxwell Boltzmann distribution paradigm. An example of the outcome after this treatment is seen in Figure 3, where the ion and electron charge density are represented for irradiation at $2.7\;\mathrm{J}/{\mathrm{cm}}^2$ . The ionic distribution is seen centered around 0.7 eV with a double peak distribution of the central maxima and a slow decay towards high values of the kinetic energy. This means that there are multiple higher ionization states in the plasma, which define a wide energy spectrum. For all investigated ${\mathrm{ZrO}}_2$ samples the ion kinetic energy varies from 0.5 to 0.8 eV, while for the ${\mathrm{HfO}}_2$ samples it is from 1.2 to 2.13 eV. It is notable that the samples deposited in 1 Pa of ${\mathrm{O}}_2$ are defined by the lowest kinetic energy for the ejected charges.

Figure 3 Calculated ion (a) and electron densities (b) ejected from the ${\mathrm{ZrO}}_2$ films upon fs-laser irradiation above the ablation threshold fluence.

The electron charge density energy distribution presents maxima at low energies around two orders of magnitude lower than the ones derived for the ions. The difference is understandable, as the electrons are easily scattered during expansion and thus lose a major part of their energy. The structure of the fs plasma also needs to be considered when investigating the electron change distribution function. According to Ref. [37], the material ablated upon fs-laser irradiation contains a major nanoparticle (NP) component expanding with low kinetic energy, which contains the majority of the ablated materials and will strongly influence the electron dynamics.

In our previous work^{[ 20]}, we have shown that LP signal can be used to quantify the ablation threshold value by using the average current representation as a function of the laser fluence. Here we expand the procedure by analyzing the variation of the ejected charge (Figure 4(a)) and the sample compensation charge (Figure 4(b)) as a function of laser fluence. These parameters are proportional to the overall ablated material and represent a measure of the LIDT limit. The ejected charges are considerably low in the 10 ${}^{-6}$ C range for both the TC and LP charges. A jump of three orders of magnitude in electrical charge is seen when crossing the threshold value.

Figure 4 LP total collected charge (a) and target total emitted charge (b) as functions of the laser fluence calculated for ${\mathrm{ZrO}}_2$ films.

The LIDT value is considered here as the intersection of the charge increase slope with the baseline defined by the low irradiation regime. For the example displayed in Figure 4 for the ${\mathrm{ZrO}}_2$ thin film deposited in 0.8 Pa of ${\mathrm{O}}_2$ , the LIDT value determined from the TC ( $0.81\;\mathrm{J}/{\mathrm{cm}}^2$ ) is $0.23\;\mathrm{J}/{\mathrm{cm}}^2$ smaller than that determined from the LP current ( $1.04\;\mathrm{J}/{\mathrm{cm}}^2$ ). This is due to the higher sensitivity of the TC measurements, which collect all charges generated at the surface level, while the LP signal strongly depends on the measurement geometry and charge scattering during expansion. The LIDT values determined by the LP-TC technique are in the 1.03– $2.18\;\mathrm{J}/{\mathrm{cm}}^2$ range for the ${\mathrm{ZrO}}_2$ films and in the 0.78– $1.84\;\mathrm{J}/{\mathrm{cm}}^2$ range for the ${\mathrm{HfO}}_2$ samples, depending on their oxygen content. The obtained results are in good agreement with the single-shot LIDT values reported in Ref. [38] for ${\mathrm{HfO}}_2$ ( $1.55\;\mathrm{J}/{\mathrm{cm}}^2$ ) and within the threshold limit found on ${\mathrm{ZrO}}_2$ films ( $1.25\;\mathrm{J}/{\mathrm{cm}}^2$ )^{[ 39]}. Otherwise, the LIDT value can differ considerably (i.e., from 0.5^{[ 40]} to $22\;\mathrm{J}/{\mathrm{cm}}^2$ ^{[ 38]}) when considering the multi-parameter dependence on the properties of the film and those of the laser^{[ 38, 41, 42]}.

The samples were investigated optically both in situ and ex situ and the results are shown in Figure 5. This figure shows the ${\mathrm{HfO}}_2$ and ${\mathrm{ZrO}}_2$ samples before (left), after irradiation under the 1-on-1 test (center) and after the R-on-1 test (right). The in situ microscopy performed with the IS offers real-time information about the damage evolution, spot size, peak fluence/pixel and sample surface quality, while the ex situ investigation was carried out using a confocal Leica microscope to cross-check the results. The images were measured using a 20× objective and the results were used for comparison with the LP-TC method.

Figure 5 (a) In situ microscopy images recorded with the imaging system and (b) ex situ microscope images of ${\mathrm{HfO}}_2$ and ${\mathrm{ZrO}}_2$ irradiated samples recorded before irradiation (left), after the 1-on-1 (middle) and after the R-on-1 LIDT damage tests (right). The color bar of (a) maps the local fluence ( $\mathrm{J}/{\mathrm{cm}}^2$ ) inferred from energy measurement and pixel values.

The results presented in Figure 5(a) show clear spatial modulations and light scattering related to the damage while the input fluence is increased. Thus, the spatial modulations observed within this method offer clear information about both threshold damage and permanent damage, but cannot estimate the subthreshold differences.

In Figure 6 there is a comparative representation of the LIDT values determined using the ex situ microscopy technique and the LP-TC approach proposed here. It can be observed that as an overall trend, the single-pulse LP-TC values are lower than the safe value proposed for the multipulse value determined from ex situ microscopy. This difference is seen as an increase in the detection sensitivity by a factor of 2.5 for ${\mathrm{ZrO}}_2$ samples and 1.8 for ${\mathrm{HfO}}_2$ . Let us note that the single-pulse LP-TC bypasses the statistical analysis often required by optical methods which take into account changes in the irradiated areas. This result represents an important step towards real-time and in-operandum monitoring of optical devices in high-power laser facilities. The elevated sensitivity of the electrical method is expected, as it is based on electrical charge imbalance induced by the fs-laser thin film interaction.

Figure 6 Comparison of the LIDT values determined from ex situ microscopy and the LP-TC approach for ${\mathrm{HfO}}_2$ (a) and ${\mathrm{ZrO}}_2$ (b) films fabricated in 0.8 Pa ${\mathrm{O}}_2$ .

The ex situ optical microscopy method only validates the threshold after clear destruction of the films by discoloration^{[ 41]}, surface modification^{[ 42]}, filamentation^{[ 43]} or crater formation^{[ 40]}. All of these mechanisms are preceded by electron emission from the film; thus, the LP-TC in the single-shot irradiation approach is designed to have increased sensitivity. Let us note the difference between the value determined by the LP versus the TCs. The threshold value determined by the TCs, induced by a charge imbalance at the film surface, has a 1.3 increase in sensitivity compared with the LP data. This difference is given by the dependence of the LP approach on the probe–film distance and the evaporation solid angle of the electrons, an aspect discussed in detail by our group in Ref. [44].

When extending the LP approach to samples produced in various oxygen pressures, the LP-TC limit is always found to be lower than the 1000 pulse optical value. While the effect of ${\mathrm{O}}_2$ pressure on the quality of the films has been investigated before in Refs. [45,46], the LP-TC method is able to give, in a single-pulse measurement, an LIDT value close to a high repetition rate working regime for dielectric thin films. The quantity of the ${\mathrm{O}}_2$ during the deposition affects the stoichiometry of the film, and thus it is known to induce specific vacancies or interstitial oxygen in the film. Rudolph et al. ^{[ 14]} reported that the presence of the midgap states effectively reduces the number of infrared (IR) photons needed for multiphoton ionization, which seeds free electrons for avalanche formation, leading to damage^{[ 47]}.

Figure 7 LIDT value calculated from ex situ microscopy and the LP-TC method as a function of the metal-to-oxide ratio for the ${\mathrm{HfO}}_2$ and ${\mathrm{ZrO}}_2$ samples.

Figure 8 Comparison between the LIDT fluence predicted for a very large number of shots and the value obtained with electrical measurements, for films of ${\mathrm{HfO}}_2$ (a) and ${\mathrm{ZrO}}_2$ (b) obtained in different oxygen background pressures. The LIDT values determined by the irradiation of one site with multiple laser pulses are shown with dots. The solid lines are obtained by fitting these values with an analytical function. The dashed horizontal lines indicate the values obtained with electrical methods.

The presence of oxygen defects leads to a decrease in the bandgap value as well as the LIDT determined by ex situ optical microscopy^{[ 45]}. When comparing the data derived for all the irradiated samples (Figures 7(a) and (b)), we observe a correlation between the oxygen pressure used during the deposition of the samples and the LIDT value. The highest LIDT values were found for the deposition in 1 Pa of ${\mathrm{O}}_2$ . This ${\mathrm{O}}_2$ pressure corresponds, according to the Rutherford back scattering (RBS) measurements, to a ratio of 2.17 O:Zr and 2.4 O:Hf. For both ${\mathrm{ZrO}}_2$ and ${\mathrm{HfO}}_2$ across the ${\mathrm{O}}_2$ pressure range that was investigated here, based on NRBS measurements, a 5% increase in oxygen quantity in the film from 0.8 to 1 Pa coupled with a 4% decrease in Zr and Hf content in the films was determined. The further addition of ${\mathrm{O}}_2$ during deposition leads to an increase of 4% oxygen incorporation and a decrease of 4% of Zr in the ${\mathrm{ZrO}}_2$ films, while for the ${\mathrm{HfO}}_2$ films there is a 7% variation of both elements. The ${\mathrm{O}}_2$ pressure during the deposition process has a stronger impact on the optical properties of ${\mathrm{HfO}}_2$ , while the ${\mathrm{ZrO}}_2$ films are more robust.

In order to confirm that the values found by the LP-TC method are relevant to the LIDT phenomena in the context of high-power infrastructures, the results were compared with the theoretical extrapolation fitting equation defined in ISO 21254-2:2011(E)^{[ 48]}. The LIDT fluence ${H}_{\mathrm{Th}}$ as a function of the number of pulses ( $N$ ) for S-on-1 test damage is defined by the standard as

(2) $$\begin{align}{H}_{\mathrm{Th}}(N)={H}_{\mathrm{Th},\infty (\mathrm{LPTC})}+\frac{H_{\mathrm{Th},1}-{H}_{\mathrm{Th},\infty (\mathrm{LPTC})}}{1+{\delta}^{-1}\cdot {\log}_{10}(N)}.\end{align}$$

The extrapolation curve is related to three fitting parameters, namely ${H}_{\mathrm{Th},1}$ , the 1-on-1 damage threshold; ${H}_{\mathrm{Th},\infty }$ , the endurance limit of the optical surface; and $\delta$ , a parameter that describes the characteristic damage curve with the number of pulses.

The LIDT values determined by the LP-TC method were integrated into the context of Equation (2) through ${H}_{\mathrm{Th},\infty }$ . By setting the endurance limit as the value estimated by the LP-TC method, it is possible to reconstruct the ${{H}}_{\mathrm{Th}}(N)$ function for all the investigated samples. The results are presented in Figure 8 (solid lines). Each curve corresponds to a set of simulated values that are asymptotically reached after ${10}^3$ shots of the LIDT value determined by the LP-TC method. When adding the ex situ microscopy data to this representation, one can observe that the points fall well within the evolution defined by the theoretical traces. The result has a profound impact on the understanding and the advantages of the LP-TC method. The single-pulse measurement of the charge imbalances in the irradiated film is naturally correlated with the long-term irradiation stability of the thin films. Moreover, this coherence between the ex situ microscopy and LP-TC approach promotes the methods proposed here as reliable for real-time in-operandum control of the optical components.

4. Conclusion

An alternative method for LIDT estimation is presented here based on a combination of an LP and compensation current measurement. The method was implemented for fs irradiation of ${\mathrm{HfO}}_2$ and ${\mathrm{ZrO}}_2$ films produced by PLD in various ${\mathrm{O}}_2$ conditions. Analysis of the electron charge density energy distribution in subthreshold conditions was performed. For laser fluences above the LIDT value, the emitted charge from the thin film increases exponentially. The LP-TC method identifies the damage point quickly, and in a similar way as standard scattering, reflectance or transmittance detection methods^{[ 16]}, but with less experimental complexity. The higher sensitivity for the LIDT values determined by the TC when compared to the LP approach is in line with the fundamental processes describing subthreshold charge dynamics. When comparing with standard LIDT measurements, 1:1 to 1000:1 with the LP-TC measurements and with the TC measurements, it is shown that the LP-TC measurements provide an indication of damage at fluences below the standard LIDT in the single shot, while in 1000:1 cases the standard LIDT measurement can exceed the LP-TC value. In contrast, the TC measurements indicate electronic processes taking place at even lower fluences, below the 1000:1 standard LIDT. Hence, it is also conjectured here that the TC measurements correspond to the infinity-extrapolated damage threshold. In this way, a conservative LIDT value that predicts the optical component resistance for very long laser exposure can be extracted more quickly and used for the practical implementation of optical components in high-power laser systems.