Diamond Raman laser: a promising high-beam-quality and low-thermal-effect laser

Abstract

Stimulated Raman-scattering-based lasers provide an effective way to achieve wavelength conversion. However, thermally induced beam degradation is a notorious obstacle to power scaling and it also limits the applicable range where high output beam quality is needed. Considerable research efforts have been devoted to developing Raman materials, with diamond being a promising candidate to acquire wavelength-versatile, high-power, and high-quality output beam owing to its excellent thermal properties, high Raman gain coefficient, and wide transmission range. The diamond Raman resonator is usually designed as an external-cavity pumped structure, which can easily eliminate the negative thermal effects of intracavity laser crystals. Diamond Raman converters also provide an approach to improve the beam quality owing to the Raman cleanup effect. This review outlines the research status of diamond Raman lasers, including beam quality optimization, Raman conversion, thermal effects, and prospects for future development directions.

1. Introduction

Wavelength-versatile and narrow-linewidth laser sources with high power and high beam quality are of broad interest in applications such as directional energy, material processing, and remote sensing^{[ 1 – 3 ]}. For a long time, researchers have been advancing towards wavelength versatility and improving output power while ensuring brightness in the laser development process. However, in traditional inversion lasers, the output wavelength range is limited owing to the inherent energy level structure of the gain medium. The inversion laser uses the accumulation of the upper-level inverted particles in the resonant cavity to achieve ‘energy storage’ and output, so the gain time is affected by the life of the particles. In addition, with the increase of pump power, the accumulated heat in the gain medium leads to thermal effects (such as thermal lensing, thermal-induced birefringence, and thermal stress fracture), resulting in deterioration of the beam quality.

Stimulated Raman scattering (SRS), a third-order nonlinear effect, is an effective method for the wavelength conversion, including the Stokes photon generation and amplification process^{[ 4 ]}. Raman lasers based on SRS are widely used to expand the spectral range and achieve complete gain amplification. The Raman gain depends on the intensity of the pump light directly, which avoids the ‘energy storage’ present in lasers that use population inversion. As a result, Raman lasers can easily achieve excellent characteristics such as single longitudinal mode (SLM) oscillation under high-power lasers. In addition, Raman lasers are also an effective device for obtaining wavelengths with excellent beam quality, and its automatic phase-matching can effectively alleviate the thermal dephasing problem in the Raman conversion process, which can play a ‘cleanup’ effect for the output laser beam and lay a foundation for obtaining high-brightness output^{[ 5 , 6 ]}.

Raman gain coefficient is the key factor in Raman lasers. Given the fact that solid media have relatively high gain coefficients and good mechanical properties, people often use solid Raman materials to study Raman conversion in different operation modes. Solid materials also need to meet the characteristics of high thermal conductivity, high damage threshold, and wide spectral transmittance to address the demand for excellent sources in many applications. Several common parameters are listed in Table 1. The comparison of these materials shows that diamond has a high Raman gain coefficient, large Raman shift, relatively narrow Raman linewidth, and wide spectral transmission range which can span deep ultraviolet, visible, near-infrared, and mid-infrared wavelengths. Diamond also has extremely high thermal conductivity, which is two to three orders of magnitude higher than that of other Raman crystals^{[ 23 ]}, and its thermal expansion coefficient is lower. The extremely high stability can minimize the influence of thermal effects under higher pumping conditions. The excellent characteristics outlined previously have led to diamond being identified as an outstanding Raman material in the laser field. Breakthrough results have been achieved in many aspects, such as the output power, wavelength conversion, and quality optimization. In this paper, we mainly describe the research progress on output characteristics and thermal effects, with prospects for the future development directions of diamond Raman lasers (DRLs) also outlined.

Table 1. Comparison of parameters between diamond and several commonly used Raman gain materials.

^a The phonon-dephasing time T ₂ and the linewidth $\Delta v$ are related through T ₂ = (πc $\Delta v$ )⁻¹.

^b Owing to indirect bandgap transitions, 1064 nm radiation is absorbed at room temperature.

^c There is moderate multi-phonon absorption in the range 2.5–6 μm.

Figure 1. Achieved output power of DRLs^{[ 8 , 23 , 28 – 43 ]} compared with other crystalline Raman lasers^{[ 33 , 44 – 53 ]} and Raman fiber lasers^{[ 54 – 61 ]}.

2. Development of DRLs

Over the past several decades, it has been shown that Raman scattering exists in natural diamond, but its small size, low purity, and spatially varying birefringence are not suitable for Raman laser materials^{[ 24 , 25 ]}. Benefiting from the continuous development of chemical vapor deposition (CVD) technology, the quality of diamond has finally met the demand for Raman gain media^{[ 26 , 27 ]}. Picosecond pulse^{[ 28 , 29 ]}, continuous-wave (CW)^{[ 23 , 30 – 33 ]}, nanosecond pulse^{[ 34 – 39 ]}, and quasi-CW^{[ 8 , 40 – 43 ]} lasers have been realized by using diamond as a Raman gain medium. In addition, these modes of operation are also involved in Raman lasers such as crystal^{[ 33 , 44 – 53 ]} and fiber^{[ 54 – 61 ]}. The comparison of the output power of diamond, fiber, and other crystal Raman lasers under different operation modes in the past decade is shown in Figure 1. It can be seen that the output power of Raman fiber lasers has always been the highest, reaching the kilowatt level, and its conversion efficiency has also been effectively improved. However, four-wave mixing leads to severe spectral broadening^{[ 57 , 62 , 63 ]}, and refractive index periodic modulation caused by thermal accumulation in the fiber leads to transverse mode instability^{[ 64 , 65 ]}, which makes it difficult to realize subsequent harmonic conversion and optimization of beam quality at high power. Other crystalline Raman lasers benefit from small spectral broadening, which makes it possible to generate effective harmonics or mixed frequencies. Unfortunately, ordinary Raman crystals have poor thermal performance. Even for the external Raman laser structure with independent pump and Raman cavities, it is difficult to obtain high-beam-quality and high-power laser output owing to the serious thermal effects. For DRLs, the output power increases rapidly, and its highest power is two to three orders of magnitude higher than that of any other crystalline Raman lasers. Although the power is lower than that of Raman fiber lasers, the excellent thermal properties of diamond give DRLs great potential with regards to output power, and may even surpass Raman fiber laser in the future. To understand the power-boosting process and output stability of DRLs, the external cavity DRL will be described from two aspects: pulse and CW.

2.1. Pulsed external cavity DRLs

DRLs were first studied by using high-peak-power pulsed lasers as the pump source. In 2010, Sabella et al. reported a pulsed external cavity DRL operating at 1240 nm, pumped by a 1064 nm Q-switched Nd:YAG laser with a duration of 10 ns and a repetition rate of 5 kHz^{[ 39 ]}. The first-order Stokes power at 1240 nm was 2 W under a pump power of 3.3 W. The slope efficiency was 84% which was lower than the quantum efficiency of 85.8%, mainly due to the existence of second-order Stokes power in the output beam.

Under the room temperature and cryogenic operation at 77 K, Feve et al. studied the output characteristics of a DRL by using a cryogenically cooled Yb:YAG pump laser in 2011^{[ 34 ]}. The output power reached 24.5 W at 1193 nm with a slope efficiency of 57% and a repetition rate of 40 kHz. However, compared with room temperature condition, the output characteristics of short-pulse pumped DRLs were not greatly improved and the thermal saturation phenomenon was even found in the high-power output. This may be due to the stronger thermal lens effect.

In 2012, Jelínek et al. used a 1.34 μm Nd:YAP laser as the pump source and generated the Raman beam with a wavelength of 1.63 μm, and the energy was 47 μJ at a duration of 6 ns^{[ 66 ]}. The experimental device was demonstrated in Figure 2. This is the first demonstration of 1.63 μm wavelength in an external cavity DRL.

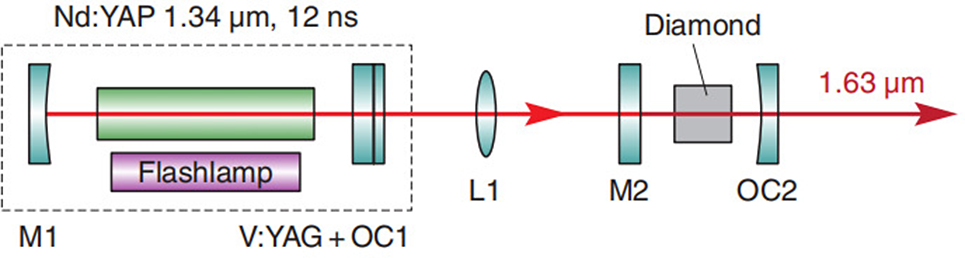
Figure 2. Schematic of the laser system consisting of a pumping Nd:YAP laser and DRL^{[ 66 ]}.

In addition, Mckay et al. reported a dual-wavelength external cavity DRL at 1240 nm and 1485 nm^{[ 16 ]}. The pump source was a 1064 nm Q-switched Nd:YVO₄ laser with a pulse width of 22 ns and a repetition rate of 36 kHz. When the input power was as high as 35 W, the dual-wavelength power was greater than 14.5 W. The slope efficiency and total efficiency of the laser were 65% and 50%, respectively. By optimizing the output coupler, the power of 1480 nm reached 11 W. In 2013, they used the same pump source to generate 30 W pump pulses, which were converted into 1.5 W first-order Stokes (1240 nm) and 13 W second-order Stokes (1485 nm) dual-wavelength beams through a Raman resonator^{[ 36 ]}. The slope efficiency and quantum conversion efficiency were 65% and 66.3%, respectively. The experimental results show that the DRL pumped by high-speed compact pump laser is expected to promote the generation of high-efficiency, high-power near-infrared laser and its harmonics.

Pashinin et al. reported an external cavity DRL with high pulse energy in 2016^{[ 67 ]}. Figure 3 shows the experimental setup. The pump laser uses a flash-pumped Q-switched Nd:YAG laser with a repetition frequency of 30 Hz and a duration of 30 ns. The dimensions of the diamond crystal in the Raman laser were 7.8 mm × 7.8 mm × 1.05 mm, and the first-order Stokes beam with energy of 1.2 mJ was generated under the pump at 20 mJ, with a slope efficiency of 54%. However, when the pump power exceeded 4 mJ, the slope efficiency decreased owing to the thermal lens effect, and even at higher pump energy, the laser would be unstable.

Figure 3. Schematic of the external cavity Raman laser^{[ 67 ]}.

From the described research of pulse pumped DRLs, it can be found that the output power of the laser does not decline even under the condition of high average pump power, which proves the excellent thermal properties of diamond. The discovery of the thermal properties of diamond also promotes an in-depth study of continuously pumped Raman lasers.

2.2. CW external cavity DRLs

Owing to the limited pumping power and the poor thermal stability of traditional gain media, continuously pumped Raman lasers started later than the pulse pumping mode versions. However, the outstanding thermal properties of diamond make it a potential candidate for CW DRLs. To effectively utilize the thermal advantage of diamond and break the bottleneck of output power, Kitzler et al. first realized high-power output by using an external cavity DRL with CW Raman conversion in 2012^{[ 31 ]}, as shown in Figure 4. The pump beam with a wavelength of 1064 nm was generated by a continuous Nd:YVO₄ laser, and then acted on the DRL through a focusing lens to generate the 1240 nm first-order Stokes beam. When the pump power reached 31 W, the output power increased to 10.1 W and a slope efficiency of 49.7% was obtained.

Figure 4. Schema of the external cavity DRL^{[ 31} .

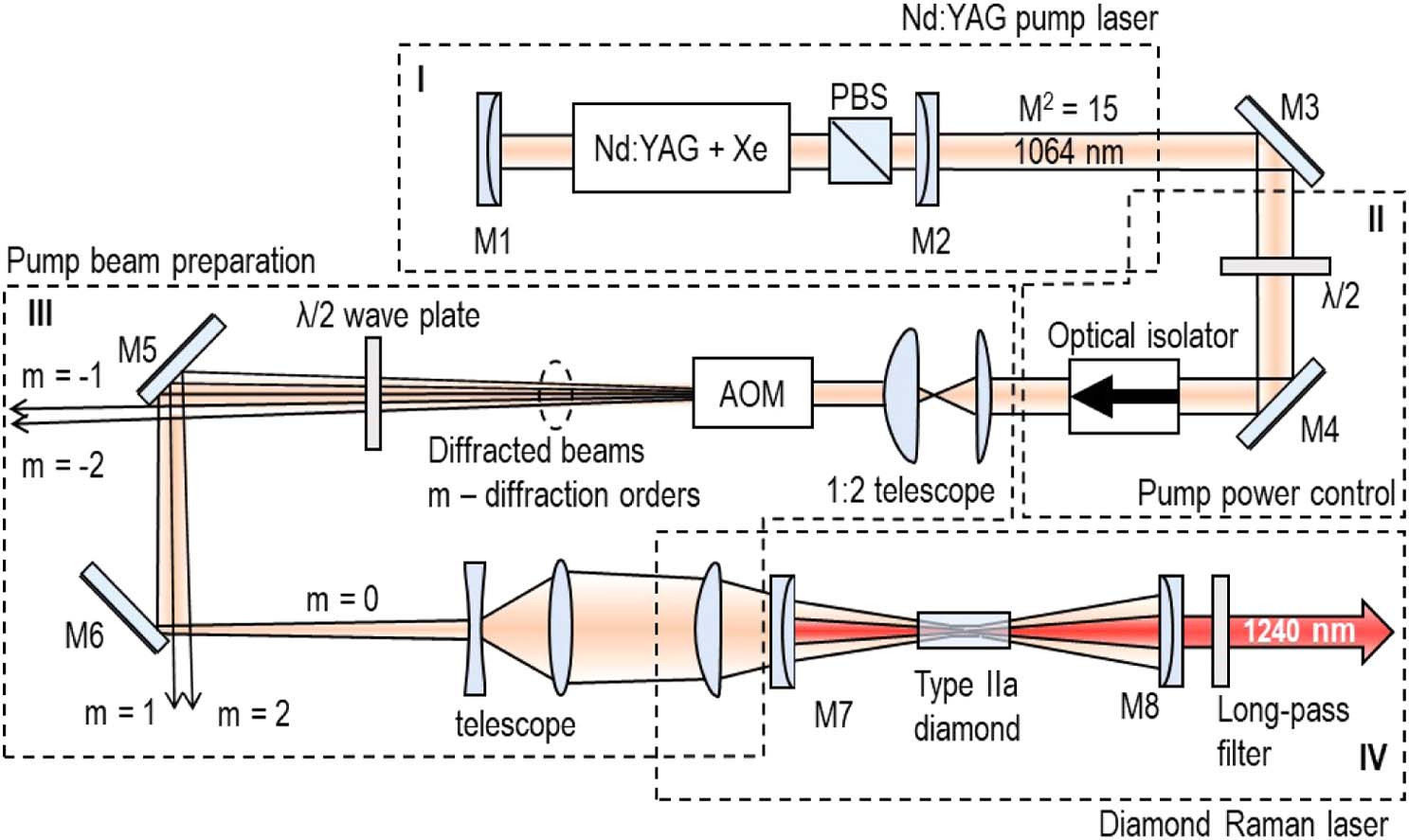
Figure 5. Layout of the external cavity DRL pumped with a Nd:YAG pulsed laser^{[ 40 ]}.

Later, the group found that for the typical pump beam waist size in the crystal, the high thermal conductivity of diamond allows the thermal gradient to be established within about 10 μs. Pulse durations longer than this are regarded as CW operation, which promotes the research of high-power characteristics of CW DRLs^{[ 41 ]}. In 2014, Williams et al. demonstrated quasi-CW operation of a DRL at 1240 nm in an external cavity configuration, pumped by a 1064 nm Nd:YAG laser^{[ 42 ]}. The power at 1.24 μm was 108 W for 322 W of pump. Owing to the low output coupling, the first-order Stokes light degraded severely during the diamond round trip, and the conversion efficiency was 34%, which was much lower than the quantum efficiency of 85.8%. It is worth noting that no power drop or change to the beam profile was observed, and it is expected that increasing pump power and first-order Stokes output coupling make it possible to achieve higher power output when the DRL operates stably. They also used a 1.06 μm Yb-doped fiber laser as the pump source and the CW laser was converted into the 1.5 μm band to study the output coupling of second-order Stokes beam^{[ 68 ]}. A record output power of 114 W at 1.49 μm was obtained by using a single cavity that is highly reflective at the first Stokes wavelength but has high output coupling at the second Stokes wavelength (89%), and demonstrated that the high output coupling of the second-order Stokes is beneficial to pump depletion and the effective conversion to the second-order Stokes beam^{[ 68 , 69 ]}.

Antipov et al. used a 4 Hz flash lamp-pumped 1.064 μm Q-switched Nd:YAG laser as the pump source with a duration of 0.5 ms to pump an external cavity DRL in 2019^{[ 40 ]}. The specific experimental device is shown in Figure 5. In the quasi-steady-state operation, the output power increased with pump power, reached 1.2 kW with an 83% slope efficiency, reaching an optical-to-optical conversion efficiency of 53%. At present, a kilowatt-level power output can be achieved in the DRL, laying a good foundation for obtaining higher-power diamond Raman conversion.

3. Output characteristics of DRLs

In addition to output power, specific wavelength, and high beam quality required for many applications, research has also been conducted on SLM, beam quality optimization, and Raman shift.

3.1. SLM

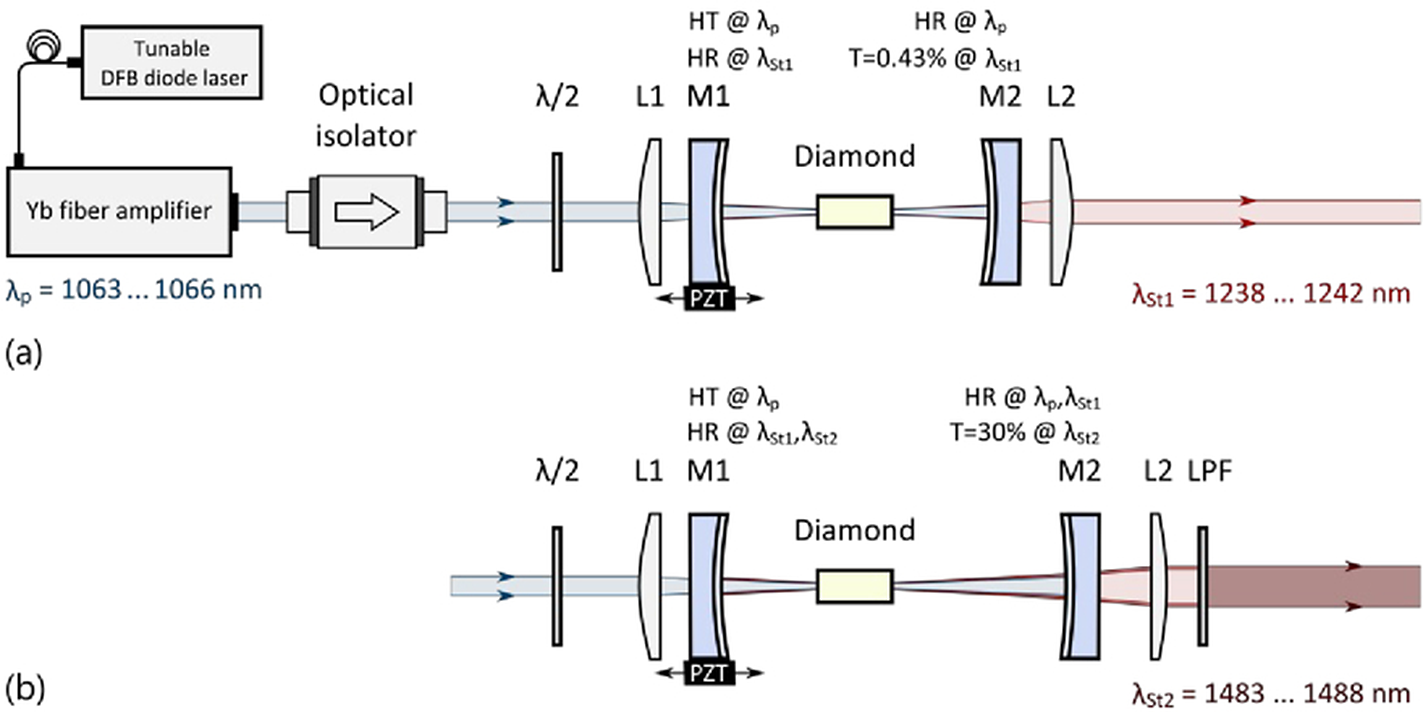
The spatial hole burning free gain of Raman lasers and the positive feedback mechanism of the resonant cavity make it possible to obtain a stable SLM. As shown in Figure 6(a), the pump wavelength tuned from 1062.8 to 1065.6 nm by changing the working temperature of a distributed feedback (DFB) laser with a thermal tuning rate of 80 pm/K, and hence the first-order Stokes wavelength was tunable in the range of 1238–1242 nm^{[ 71 ]}. The multimode output power was 14 W with a slope efficiency of 62% and a conversion efficiency of 38% at the maximum injected pump power of 37 W. In the SLM operation, the stability of the Stokes wavelength was in the range of 80 MHz over periods of several tens of seconds and the power reached 4 W with a conversion efficiency of 20%. On longer time scales, the fluctuation range was in the order of hundreds of megahertz, which was caused by the change of the optical cavity length owing to the change of thermal expansion and refractive index in the diamond. Subsequently, these authors realized the second-order Stokes beam output in the wavelength range of 1483–1488 nm by using the same pump source^{[ 72 ]}. The corresponding Raman laser device is shown in Figure 6(b). The Raman laser obtained 7 W multimode output power and 21% conversion efficiency at 34 W pump power. SLM output power from 0.1 to 0.5 W and the frequency stability was improved over a minute without active cavity stabilization by using a volume Bragg grating as an output coupler. Compared with the first-order Stokes laser, the stronger coupling between Stokes power and the optical cavity length reduced the maximum SLM output power.

Figure 6. Experimental setup of the tunable (a) first-order and (b) second-order Stokes DRL operating in SLM^{[ 70 ]}.

The mode competition provided by harmonic mixing can greatly improve the mode stability owing to the advantages of having a gain medium without spatial hole burning. In 2019, Yang et al. first realized a quasi-CW SLM operation in an external cavity DRL, pumped by a multimode 1064 nm Nd:YAG laser with a linewidth of 3.3 GHz^{[ 73]}. Without mode competition, SLM operation at 1240 nm was limited to 6.5 W. Including a LiB₃O₅ (LBO) crystal for second harmonic generation in the cavity increased the maximum SLM power to 11.8 W at 1240 nm and 38 W at 620 nm, and the power instability was less than 10%. The results show that the self-suppression provided by additional gain competition strongly reduces the instability of SLM caused by thermally induced cavity length. In 2020, the author first realized a 22 W of CW output at 589 nm with near-diffraction-limited beam quality in the diamond Raman and second-harmonic generation resonator^{[ 74 ]}. The 1018 nm ytterbium-doped fiber (YDF) laser as the pump laser consists of two parts: fiber Bragg grating oscillator and one-stage YDF amplifier. The linewidth of SLM output at 589 nm was less than 8.5 MHz and the conversion efficiency was 34.9% at 63 W pump power.

3.2. Beam quality optimization

The beam quality factor M² is defined by the beam waist width and beam divergence angle. It can describe the focusability, mode content, and other important characteristics of the laser beam, so it is an important parameter to judge the quality of laser beam^{[ 75 – 77 ]}. In addition, because this factor does not change when the beam propagates through a medium with a secondary refractive index distribution, it is possible to use the change of the beam quality factor to infer whether there is aberration^{[ 78 ]}. For this reason, the study of beam quality factor is very important in many practical laser applications, especially the study of Gaussian beam quality factor^{[ 78 – 81 ]}. The research progress on beam quality optimization of DRLs is briefly reviewed in Table 2.

Table 2. Optimization of beam quality of DRLs in recent years.

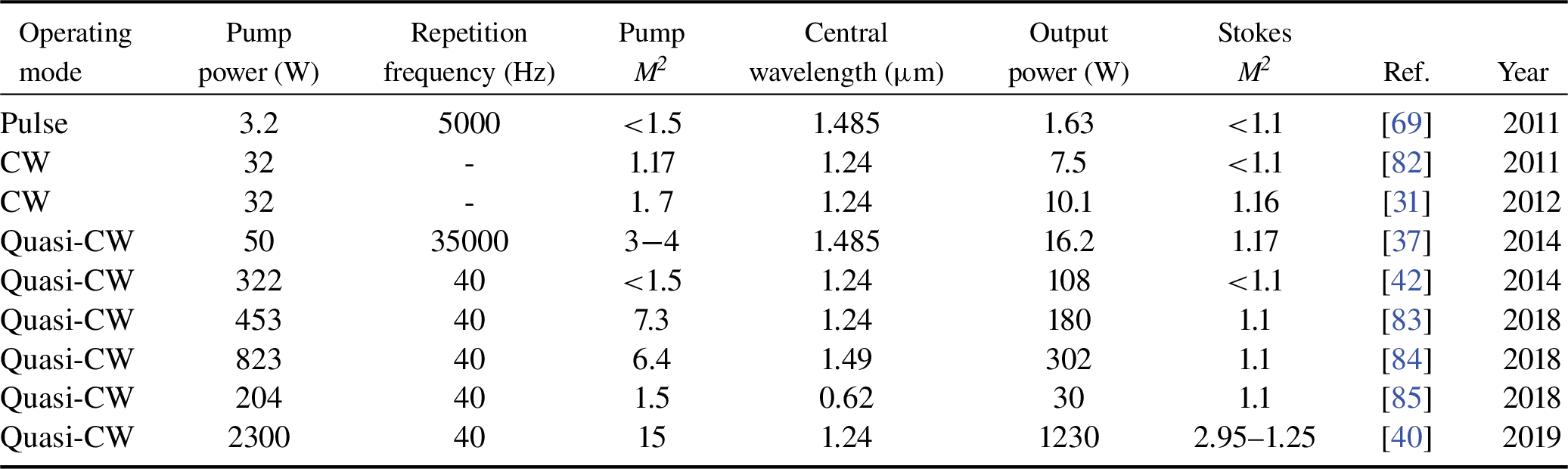
Figure 7. Spot distribution of pump and Stokes beams in DRLs^{[ 37 , 83 , 84 ]}: (a) pump spot distribution; (b) corresponding Stokes spot distribution.

In 2014, Mckay et al. studied the brightness enhancement of an external cavity DRL pumped by a nanosecond pulse^{[ 37 ]}. A multimode 1064 nm Q-switched Nd:YVO₄ laser with M ² = 3–4 was the pump source. For the second-order Stokes beam (1485 nm), the beam quality factor M ² = 1.17, was 2.7 times lower than the pump beam quality factor. Bai et al. reported a method to improve the brightness of high-power CW beams by using medium-beam-quality pumping light in 2018^{[ 83 ]}. The 1064 nm pulse pump light was generated by a quasi-CW diode-pumped Nd:YAG laser. By adjusting the current and duty cycle of the pump diode and the cavity length, the beam quality factor of the pump light ranges from M ² = 2.3 to 7.3. Under the condition of maximum pump power, the beam quality was M ² = 1.10 ± 0.03 at 1239.88 nm. The present authors also reported the brightness enhancement capability of the second-order Stokes beam (1.49 μm)^{[ 84 ]}. Using the same method, the pump beam quality can be adjusted within the range from M ² = 4.3 to 6.4, and the output beam quality was M ² = 1.1 ± 0.04. This is mainly due to the high-power processing ability and self-phase matching of DRLs. In 2019, Antipov et al. achieved a high-power output of 1.2 kW with excellent beam quality in a quasi-steady-state regime^{[ 40 ]}. When the pump power increased from 0.17 to 1.1 kW, the output beam quality factor decreased from M ² = 2.95 to 1.25, and the overall brightness increased.

Figure 8. Schematic of a cascaded DRL pumped by a 1.06 μm laser^{[ 20 ]}.

Figure 7 shows the near-field spot distribution of input and output beams obtained from some experiments of DRLs. To fully realize the ability of beam purification, a medium-beam-quality laser is generally used as the pump source. It can be seen from Figure 7(a) that the high-order spatial mode content and beam distortion in the near-field distribution of the pump beam are obvious. There is a large asymmetry in the spatial distribution, and even some astigmatism. In contrast, the output Stokes beam corresponding to the pump beam in Figure 7(b) has no beam distortion, and the spatial distribution presents a Gaussian distribution near the TEM₀₀ mode. In general, the pump light with medium beam quality promotes the output of good beam quality in DRLs.

3.3. Raman frequency shift

In addition to DRLs producing high-power and high-quality laser, lasers with different wavelengths also play a vital role in different application fields. Diamond is expected to provide a convenient and effective way for Raman conversion to a higher band because of its large Raman shift, high Raman gain coefficient, and wide transparency range^{[ 86 ]}. At present, cascaded DRLs can shift the pump light to higher-order Stokes light. Importantly, only two Stokes frequency shifts from the 1.06 μm region can obtain 1.5 μm band lasers with characteristics of eye safety and low atmospheric transmission loss, with important applications in radar^{[ 87 ]}, remote sensing^{[ 3 ]}, and other fields. The wavelength conversion process is shown in Figure 8. Compared with the six orders of silica fiber Raman^{[ 8 , 88 ]} or the three orders of BaWO₄ crystal^{[ 89 ]}, the complexity of optical coating is greatly reduced and the improvement of Raman conversion efficiency is easy to realize. In addition to the above-mentioned 1.5 μm band, DRLs also provide access to other band lasers.

In 2008, Mildren et al. used a Raman laser formulated using a Brewster-cut diamond crystal to generate first-order Stokes (573 nm) output power of up to 1.2 W when pumped with a 532 nm frequency-doubled Q-switched Nd:YAG laser^{[ 9 ]}. The experimental device and the output spectrogram are shown in Figure 9(a). When the pump power exceeded 0.28 mJ, the wavelength of 620 nm caused by the second Stokes shift was also observed.

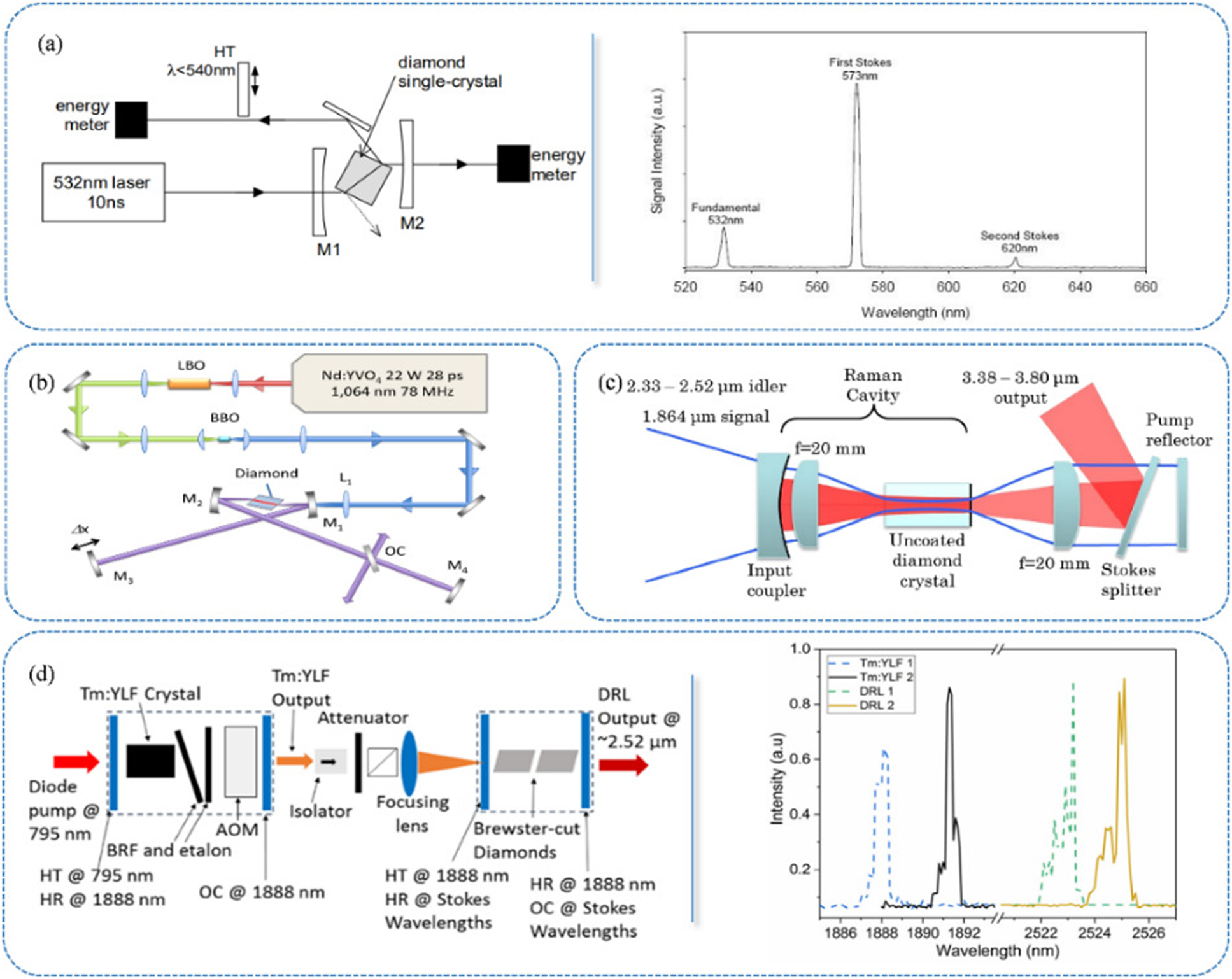
Figure 9. Different wave bands of DRLs and the related output spectra^{[ 7 , 90 – 92 ]}: (a) 573 nm and 620 nm laser output from 532 nm pump beam; (b) 275.7 nm laser output from 266 nm pump beam; (c) 3.38–3.8 μm laser output from 2.33–2.52 μm pump beam; (d) ∼2.53 μm laser output from 1.89 μm pump beam.

Granados et al. reported a DRL working at 275.7 nm in deep ultraviolet in 2011^{[ 91 ]}. The experimental setup diagram is shown in the Figure 9(b). The output beam of 275.7 nm converted by the pump beam at 266 nm in a DRL with a pulse energy of 0.96 nJ. This study showed the potential of DRL working in the deep ultraviolet, paving the way for the design of ultraviolet pumped DRL using nanosecond and CW pumped lasers.

Sabella et al. used the tunable optical parametric oscillator as the pump to generate mid-infrared pulse beam in the range of 3.38–3.80 μm in a DRL in 2014^{[ 7 ]}. The device used in the experiment is shown in Figure 9(c). The surface of the 8 mm long diamond crystal was uncoated, and one surface of the diamond crystal was used as an output coupler. Under the condition of single-wavelength pumping at 2.480 μm, it was converted to 3.705 μm by first-order Stokes shift. However, owing to the existence of multiphoton absorption, the highest average pulse energy was only 80 μJ. Later, because the frequency difference between the idler light of 2.480 μm and the signal light of 1.864 μm was exactly the diamond Raman frequency of 1332 cm^–1, Stokes seeds were generated by Raman resonance four-wave mixing which reduced the threshold value and finally achieved the highest average pulse energy of 115 μJ. The results showed that the interaction between diamond Raman frequency shift and the parametric process is effective for optimizing the mid-infrared light source, and it is possible to generate a wavelength as high as 6 μm through cascaded second-order Stokes shift.

In 2020, Demetriou et al. successfully realized an output of wavelength ∼2.52 μm at the edge of multiphoton absorption in diamond by first-order Raman conversion in an external cavity DRL pumped by a 1.89 μm Tm:LiYF₄ (YLF) laser^{[ 92 ]}. Two different Brewster-cut diamond crystals were used in the experiment, and the experimental equipment and output spectrogram are shown in Figure 9(d). When the pump energy reached 4.4 mJ, the maximum output pulse energy of 1.67 mJ was obtained. These authors also proposed that by changing the thickness of the etalon, it is expected to generate more pump wavelengths around 1.9 μm, and then expand the coverage area around approximately 2.5 μm.

Up to now, the wavelength conversion to deep ultraviolet, visible, near-infrared, and mid-infrared wavelength regions has been successfully realized through the effective combination of diamond with excellent characteristics and SRS^{[ 7 , 90 – 93 ]}. However, with the increase of pump power and cascade times, not only the mirror coating process will limit the development of cascaded Raman lasers, but also the increasing thermal effects in the diamond crystal may become an important factor.

4. Thermal effects of DRLs

Thermal effects are one of the main problems that limit the increase in power. The main reason is that during the operation, in addition to obtaining the required laser light source, part of the energy is accumulated in the crystal in the form of heat. As a result, negative thermal effects such as thermal lens and thermal birefringence would make the laser cavity unstable and change the spatial distribution of the laser beam. Finally, the output power would decline, the beam quality degrades, and even irreversible phenomena such as power damage of the working substance would occur^{[ 47 , 94 – 96 ]}.

Owing to severe thermal effects, the laser generated by the traditional way can no longer meet the demand for high-power and high-quality lasers in the current application field, which means that solving thermal effects is the key to obtaining excellent laser output. Therefore, several evaluations and compensation methods of thermal effects in the frequency conversion process are discussed for different crystal materials, such as Ba(NO₃)₂ and Yb³⁺:KGd(WO₄)₂ (KGW). Experiments show that the insertion of additional lenses, the stable structure of the Raman cavity, and the cutting direction of the crystal can reduce the thermal lens effect, and the thermal expansion of the end face increases with the increase of the ratio of the radius to the length of the crystal, but the change of refractive index does not^{[ 47 , 49 , 97 – 99 ]}. Therefore, people can reduce the surface temperature of the medium (such as water cooling, semiconductor refrigeration, and liquid nitrogen refrigeration)^{[ 100 , 101 ]} to make the working material in a relatively low temperature or constant temperature environment, and then further improve the surface area of heat dissipation by changing the structure of laser gain media (such as optical fiber^{[ 1 , 102 ]}, slab^{[ 103 , 104 ]}, and disk^{[ 105 , 106 ]}). Although these methods alleviate the influence of thermal effects on laser gain media to a certain extent, they have not found an effective solution fundamentally (such as inherent physical properties and spectral properties of the working substance).

The excellent properties make diamond a good candidate for Raman lasers. However, to improve and optimize the output beam power and beam quality again under higher pumping conditions, the consideration of thermal effects inside the cavity cannot be ignored. The thermal effect of DRLs through the combination of related diamond Raman experiments and the evolution of existing crystal thermal effect models is an important future research direction.

4.1. Theoretical analysis of the thermal effects of DRLs

The thermal distribution and thermal lens effect in diamond with first-order Stokes output were modeled and calculated by a finite-element-analysis transient heat solver in two dimensions (QuickField). The method of analyzing thermal lens evolution using QuickField has long been confirmed. For example, in the study of high-power KGW Raman laser, the near-field distribution was transformed from low-order mode to elongated Hermite–Gaussian mode, and under the condition of high duty cycle and output coupling curvature, the output efficiency decreased and the extension of near-field beam profile increased further. Compared with the calculated results of the axial temperature change and the evolution of the maximum gradient in the crystal, it was inferred that the gradient was the main reason for efficiency reduction and multimode spatial characteristics^{[9 8 ]}. Similarly, the thermal lens effect in DRLs has been studied.

In view of the interaction relationship between the thermal lens and the first-order Stokes output in the external cavity DRL, the corresponding models are designed to predict and estimate the intensity of the thermal lens in the crystal under pulse and CW operation modes. In CW operation, if the confocal parameter of pump beam is larger than the crystal length and smaller than the confocal parameter of Stokes beam, it is reasonable to assume a gradient index lens with a fixed refractive index along the optical axis direction and a parabolic refractive index lens with a distance r from the center of the beam in the lateral direction^{[ 107 ]}, as follows:

(1) $$\begin{align}n(r)={n}_0-\frac{1}{2}{n}_2{r}^2,\end{align}$$

where ${n}_0$ is the refractive index of diamond at 1240 nm^{[8 6 ]}, ${n}_2$ is the parabolic parameter of the refractive index, and we obtain

(2) $$\begin{align}{f}^{-1}={n}_2l,\end{align}$$

where $l$ is the length of the diamond crystal, the focal length of thermal lens is calculated by modifying the expression of CW end-pumped rod laser, which is derived from the profile of top-hat pump beam^{[ 86 , 108 ]}:

(3) $$\begin{align}{f}^{-1}=\frac{P_{\mathrm{dep}}}{2\pi {{kw}}_0^2}\left[\frac{\mathrm{d}n}{\mathrm{d}T}+\left({n}_0-1\right)\left(v+1\right){a}_T+{n}_0^3\alpha {C}_{r,\phi}\right],\end{align}$$

where ${P}_{\mathrm{dep}}$ is the deposited heat, which can be derived from the difference between the power consumed by the pump and the Stokes output power, $k$ is the thermal conductivity, ${w}_0$ is the waist radius of the pump beam, $\frac{\mathrm{d}n}{\mathrm{d}T}$ is the thermo-optical coefficient, $\nu$ is Poisson's ratio, ${\alpha}_T$ is the thermal expansion coefficient, and ${C}_{r,\phi }$ are the photoelastic coefficients. For diamond crystal, the main factors of the thermal lens are thermo-optic effect and end-face curvature, and the relatively weak photoelastic effect can be ignored^{[ 86 ]}.

The modification of this model is represented by introducing a correction factor. To reduce the error, this factor takes into account the mismatch between the pump and laser modes in the top-hat or Gaussian pump beam profile^{[ 109 ]}:

(4) $$\begin{align}\mathrm{Top}\hbox{-} \mathrm{hat}:r(x)=1.1-0.74x+1.22{x}^2,\end{align}$$

(5) $$\begin{align}\mathrm{Gaussian}:r(x)=1+2{x}^2,\end{align}$$

(6) $$\begin{align}{f}_{\mathrm{corr}}^{-1}=\frac{f^{-1}}{r(x)},\end{align}$$

in which 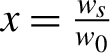$x=\frac{w_s}{w_0}$ is the ratio of Stokes and pump waist radius.

In the case of pulse output, it is assumed that the energy of the first-order Stokes beam generated by the laser is ${E}_{\mathrm{St}}$ , and the corresponding energy dissipated to heat in the Raman process is (as for the source of heat, only the attenuation of optical phonons produced by Raman scattering is considered)

(7) $$\begin{align}\left(\frac{{{hv}}_{{R}}}{{{hv}}_{\mathrm{St}}}\right)\cdot {E}_{\mathrm{St}}=\left(\frac{1332\;{\mathrm{cm}}^{-1}}{8066\;{\mathrm{cm}}^{-1}}\right)\cdot {E}_{\mathrm{St}}=0.165\cdot {E}_{\mathrm{St}},\end{align}$$

where $h{v}_{\mathrm{R}}$ is phonon energy and $h{v}_{\mathrm{St}}$ is the Stokes photon energy. During the pump pulse duration, the thermal diffusion length in diamond can be estimated by the following formula^{[ 110 ]}:

(8) $$\begin{align}{L}_d\sim {\left( D\tau \right)}^{\frac{1}{2}},\end{align}$$

in which D ≈ 12 cm^–1⋅s^–1 is the diffusivity of diamond^{[ 111 ]}. If the estimated value is far smaller than the beam diameter, the thermal diffusion length of diamond can be ignored, which is not considered in the following calculation. As refractive index change and crystal distortion are related to temperature change, the Gaussian radial distribution of beam energy can be expected to be output according to the radial temperature distribution $\delta T(r)$ ^{[ 67 ]}. With respect to axial distribution, if the transverse size of diamond is less than the pulse time diffusion length, the temperature before the next pulse is almost uniformly distributed:

(9) $$\begin{align}\delta T(r)=0.165\times {E}_{\mathrm{St}}\times 2/\left(\pi \cdot {w}^2\cdot \rho \cdot l\cdot {C}_{\rho}\right)\times \exp\;\left(-\frac{2{r}^2}{w^2}\right).\end{align}$$

In this formula, $w$ is the mode radius, $\rho$ is the mass density of diamond, and ${C}_{\rho }$ is the heat capacity of diamond. For the parabolic approximation of the temperature curve, the focal length ${F}_t$ of the induction lens is calculated by the following formula^{[ 67 ]}:

(10) $$\begin{align}{F}_t^{-1}&=l\cdot \left[n\frac{\mathrm{d}n}{\mathrm{d}T}+\left(n-1\right)\alpha \right]\cdot \left(\frac{\mathrm{d}^2T}{{\mathrm{d}r}^2}\right)\notag\\&=0.66\cdot {E}_{\mathrm{St}}\cdot \left[n\frac{\mathrm{d}n}{\mathrm{d}T}+\left(n-1\right)\alpha \right]\left/\left(\pi \cdot {w}^4\cdot \rho \cdot {C}_{\rho}\right)\right..\end{align}$$

As the thermal expansion coefficient of diamond crystal is several orders of magnitude lower than that of thermo-optic coefficient, the thermal expansion term in Equation (10) can be ignored.

4.2. Negative thermal effects

The excellent thermal conductivity of diamond compared with other Raman active media enables it to achieve equivalent power output without being affected by heat, and there is no distortion of beam. When the average power is higher, the heat deposited in the diamond is not enough to affect the output power. In order to obtain high-average-power Stokes radiation and cascade to high-order Stokes beam, DRLs usually work under the condition of strong focus. At this time, the power density in the crystal center is higher and the internal temperature is higher. Thermal effects may become an important factor limiting the average power of DRLs. Despite the excellent thermal properties of diamond researchers have observed some phenomena in experiments, and further research and discussion are made on thermal effects.

In 2015, Williams et al. realized pulse and CW operation in a double-pass pumped external cavity DRL, in which the pump light came from a YDF laser. Under the action of pump light with a linewidth of 0.16 nm, high noise was observed in Stokes output power, and one possible factor was the influence of thermal change in the cavity. To estimate the thermal lens in the DRL, it is assumed that the thermal deposition was uniformly distributed along the crystal length, and only the contribution of thermo-optic effect to thermal lens is considered, mainly because the end-face curvature and photoelastic effect are several orders of magnitude weaker. At the output power level of 381 W, the focal length of 5.9 mm thermal lens caused by Raman phonons is calculated according to Equation (3), whereas the thermal lens strength caused by Stokes beam absorption is weaker by more than one order of magnitude and neglected. The focal length has exceeded the stability limit of the cavity (f _min = 28.7 mm), and led to the increase of Raman mode size of the diamond. It was expected that under a pump power as low as 200 W, the efficiency would decrease and the output beam would deteriorate owing to the influence of the thermal effect. However, the predicted result was quite different from the experimental observation result: one key factor was that the influence of the mismatched pump beam and Stokes beam on the thermal lens intensity is greatly intensified and cannot be ignored owing to the fact that the pump beam is significantly smaller than the Stokes beam, and because the pump beam profile is Gaussian^{[ 43 , 107 ]}.

Pashinin et al. used a 1064 nm Q-switched Nd:YAG laser as a pump source, and realized high pulse energy output at 1240 and 1480 nm in an external cavity DRL in 2016. However, in the process of first-order Stokes output at 1240 nm, the efficiency decreased when the pump energy exceeded 4 mJ. Pashinin et al. speculated that it may be caused by the thermal lens effect in the resonant cavity, so the pulse theory model was used to further verify whether it is related to the thermal lens effect. The thermal lens strength was calculated by Equation (10) in the thermal lens model. When the energy E was 0.45 and 0.55 mJ, the focal length F of the thermal lens was 114 and 93 mm, respectively. In this case, the thermal lens effect could be further alleviated by increasing the diameter of the mode. However, when the energy exceeded 0.6 mJ, increasing the mode diameter made the resonator unstable. The result showed that at some point in the Stokes pulse, the increase of the mode diameter begins to limit the further enhancement of the thermal lens, but leads to a small Raman gain. This confirmed that the observed reduction of conversion efficiency under high pump energy was caused by the thermal lens effect in the cavity^{[ 67 ]}.

Jasbeer et al. achieved high-power output at 620 nm in a quasi-CW external cavity DRL by intracavity frequency doubling of LBO crystal in 2018. The author also proposed that with the increase of pump power and duration, the thermal effect of intracavity crystals cannot be ignored. When the output power was 30 W, the thermal load generated by diamond Raman phonon was 6.7 W, and the heat load generated by the absorption loss was 3.2 W. The focal length of the thermal lens was 18 cm according to Equation (3). Note that only the thermo-optic term was considered here. ABCD analysis showed that when the focal length of the thermal lens was as short as 2.6 cm, the thermal effect could be reduced by a small length adjustment, and the inferred focal length value was at least one order of magnitude weaker than the limit of the stability of the cavity. The thermal effects of LBO crystal should also be considered because of the realized frequency doubling output. Finally, the thermal lens of diamond and LBO crystal was expected to obtain the output power of 95 W at 320 W pump^{[ 69 ]}.

In pumping a 1.2 kW external cavity DRL, Antipov et al. observed that the output beam quality factor decreased with the increase of the pump power in 2019^{[ 40 ]}. It was speculated that the occurrence of this phenomenon may be attributed to the good thermo-optic coefficient of the diamond crystal. With the increase of thermal load in the near concentric cavity, the TEM₀₀ mode radius increased. It means that the overlap area between the basic Stokes mode and the pump increased, thus increasing the power ratio coupled to the TEM₀₀ mode.

In addition, ABCD calculation showed that it takes 10 diopters to increase Stokes mode size by 20%, whereas the lens strength calculated by experiment reached 14.6 diopters. The comparison of data also showed that there was thermal lens effect in the diamond. To verify this conjecture, the author used the same configuration and cavity design as the DRL pump laser to analyze the thermal lens effect and output beam of the DRL in 2020^{[ 107 ]}. The experimental device for characterizing the external cavity DRL output beam is shown in Figure 10(a). The results showed that the beam quality factor and divergence angle of Stokes beam decreased with the increase of output power. The thermal lens strength was 16 diopters at most, and the thermal lens had little influence on the pump beam, and the change in dimension was less than 1%. Comparing the experimental results with the thermal lens model mentioned previously, although there was a certain deviation between the experimental result and the calculated value of the model, the overall trend of the two was consistent as shown in Figure 10(b). It was verified that the increase of output beam quality was due to the increase of thermal lens when the output power exceeded 0.4 kW.

Figure 10. High-power DRL pumped by Nd:YAG pulsed laser^{[ 107 ]}: (a) experimental setup of the DRL and output beam characteristics; (b) thermal lens strength as a function of Stokes output power.

5. Summary

The outstanding properties of diamond make it an excellent material for high-power, high-beam-quality Raman lasers. So far, many works have focused on quality optimization, wavelength expansion, output power, and conversion efficiency by using DRLs. Its high Raman gain coefficient and wide transparency range promote the improvement of efficiency and wavelength conversion. High thermal conductivity and low thermal expansion promote high efficiency and near diffraction limited quality, and have successfully achieved kilowatt power comparable to Raman fiber lasers. In addition, the highest output power of Brillouin laser has been obtained by using diamond^{[ 112 , 113 ]}.

However, with the increase of power, DRLs are usually operated under the condition of strong focusing. At this time, the internal power density of the diamond crystal gradually increases, which may lead to negative factors such as the thermal effect. Among them, the existence of thermal effects in the resonant cavity has been observed in the DRL with kilowatt power, and the problem and analysis model of the thermal lens effect in a diamond gain medium have also been proposed. The decay properties of Raman photons and the uncertainty of the distribution of decay products have always been key factors for the immature thermal analysis of DRLs. Therefore, in the future, the sources and distribution of heat in diamond crystals will be the focus of research. From the aspect of a thermal analysis model, it is necessary to control the uneven depletion of pump beam and subsequent diffraction in the thermal analysis model effectively to minimize the error. In addition, given the fact that there is no spatial hole burning in the Raman conversion process and the mode competition provided by harmonic mixing, the stable operation of SLM in DRLs is realized. Although most of the thermal effects of DRLs are analyzed under steady-state conditions, few studies have been reported under other modes. It is of great significance to understand how thermal effects affect the performance in different operating modes and determine effective solutions for achieving higher-power, higher-conversion-efficiency, and higher-brightness DRLs output and cascade in different fields in the future.