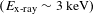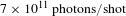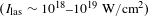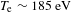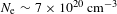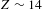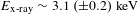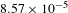1 Introduction
Laser-produced plasma as a bright, point-like, pulse source of X-ray radiation in the energy range from 0.1 to 50 keV has been actively investigated in the past decades[Reference Popmintchev, Chen, Popmintchev, Arpin, Brown, Ališauskas, Andriukaitis, Balčiunas, Mücke, Pugzlys, Baltuška, Shim, Schrauth, Gaeta, Hernández-García, Plaja, Becker, Jaron-Becker, Murnane and Kapteyn1–Reference Rousse, Ta Phuoc, Shah, Pukhov, Lefebvre, Malka, Kiselev, Burgy, Rousseau, Umstadter and Hulin4]. The power of X-ray source and emission efficiency are determined by laser plasma parameters, which in turn strongly depend on experimental conditions. For highly intense X-ray source formation in laser-produced plasma, usually foil targets made of a material with a high atomic number  $Z\sim 30{-}50$ are used. To provide high efficiency of K-shell ionization processes in targets with
$Z\sim 30{-}50$ are used. To provide high efficiency of K-shell ionization processes in targets with  $Z\geqslant 25$, it is necessary to provide conditions for fast electron impact inner-shell ionizations[Reference Serbanescu, Fourmaux, Kieffer, Kincaid and Krol5] using non-relativistic laser pulses or to heat them up to temperatures about 2–5 keV. This is possible only via high-contrast laser pulses with peak power
$Z\geqslant 25$, it is necessary to provide conditions for fast electron impact inner-shell ionizations[Reference Serbanescu, Fourmaux, Kieffer, Kincaid and Krol5] using non-relativistic laser pulses or to heat them up to temperatures about 2–5 keV. This is possible only via high-contrast laser pulses with peak power  ${\sim}0.3{-}1~\text{PW}$, i.e., pico- and femtosecond laser pulses with ultra-relativistic intensities
${\sim}0.3{-}1~\text{PW}$, i.e., pico- and femtosecond laser pulses with ultra-relativistic intensities  $(I_{\text{las}}\geqslant 10^{21}~\text{W}/\text{cm}^{2})$. Plasma generated under these conditions is a bright source not only of keV X-ray photons with flux density up to
$(I_{\text{las}}\geqslant 10^{21}~\text{W}/\text{cm}^{2})$. Plasma generated under these conditions is a bright source not only of keV X-ray photons with flux density up to  $10^{12}{-}10^{13}$ photons/shot, but also of different particles’ beams: electrons, protons and neutrons. Since a laser plasma can be labeled as a ‘clean’ X-ray source when it is debris free, its X-ray emission is rather intense and dominates over fast particle emission. The ultra-relativistic laser plasma of solid-state foils is considered a pulsed, intense, but not clean X-ray source. Despite this, such a plasma as a pulsed source of X-ray radiation is widely used for fundamental research, for example, in the fields of indirect inertial confinement fusion and high energy density physics. However, the presence of the intense corpuscular emission is significantly complicating and often makes it impossible to use the X-ray radiation from ultra-relativistic laser plasma for practical applications for lithography and absorption or phase-contrast radiography of plasma, nanostructured and biological objects.
$10^{12}{-}10^{13}$ photons/shot, but also of different particles’ beams: electrons, protons and neutrons. Since a laser plasma can be labeled as a ‘clean’ X-ray source when it is debris free, its X-ray emission is rather intense and dominates over fast particle emission. The ultra-relativistic laser plasma of solid-state foils is considered a pulsed, intense, but not clean X-ray source. Despite this, such a plasma as a pulsed source of X-ray radiation is widely used for fundamental research, for example, in the fields of indirect inertial confinement fusion and high energy density physics. However, the presence of the intense corpuscular emission is significantly complicating and often makes it impossible to use the X-ray radiation from ultra-relativistic laser plasma for practical applications for lithography and absorption or phase-contrast radiography of plasma, nanostructured and biological objects.
The point is that for most of practical applications the criterion of plasma X-ray source ‘purity’ and its high repetition frequency becomes designating. Since accelerated corpuscular beams create a noise background on a detector, it prevents obtaining of a high-quality image of an investigated object. Thus, a solution for the problem of generating a clean X-ray source in a laser-produced plasma can be found by optimization of the laser–matter interaction conditions, which implies selecting such conditions and geometry of an experiment when the most part of the main laser pulse energy converts to X-ray radiation, and processes of the accelerated corpuscular beams formation proceed weakly, or do not proceed at all. For instance, it is possible to decrease a number of accelerated particles emitted from a laser plasma by using laser pulses with moderate and relativistic intensities  $(I_{\text{las}}\sim 10^{16}{-}10^{19}~\text{W}/\text{cm}^{2})$. On the one hand, it also leads to decreasing of the X-ray source emission intensity by more than one order. This disadvantage can be compensated by using foam/porous/gel structures as laser targets. It was shown in Refs. [Reference Nishikawa, Suzuki, Watanabe, Zhou and Nakano6–Reference Sumeruk, Kneip, Symes, Churina, Belolipetski, Donnelly and Ditmire8] that the application of foam nanostructure targets resulted in a significant increase of X-ray emission from a laser plasma[Reference Rosmej, Andreev, Zaehter, Zahn, Christ, Borm, Radon, Sokolov, Pugachev, Khaghani, Horst, Borisenko, Sklizkov and Pimenov9]. Unfortunately for most of the cases, the production of these targets is a complicated many-step process, which makes such target application rather expensive for wide use.
$(I_{\text{las}}\sim 10^{16}{-}10^{19}~\text{W}/\text{cm}^{2})$. On the one hand, it also leads to decreasing of the X-ray source emission intensity by more than one order. This disadvantage can be compensated by using foam/porous/gel structures as laser targets. It was shown in Refs. [Reference Nishikawa, Suzuki, Watanabe, Zhou and Nakano6–Reference Sumeruk, Kneip, Symes, Churina, Belolipetski, Donnelly and Ditmire8] that the application of foam nanostructure targets resulted in a significant increase of X-ray emission from a laser plasma[Reference Rosmej, Andreev, Zaehter, Zahn, Christ, Borm, Radon, Sokolov, Pugachev, Khaghani, Horst, Borisenko, Sklizkov and Pimenov9]. Unfortunately for most of the cases, the production of these targets is a complicated many-step process, which makes such target application rather expensive for wide use.
On the other hand, the moderate laser intensities allow for increasing significantly the X-ray pulses’ repetition rate since modern laser systems are able to generate short-duration pulses with intensities  ${\sim}10^{19}~\text{W}/\text{cm}^{2}$ with frequency 0.1–10 Hz, but it implies special requirements for laser targets. A system which provides the interaction with non-perturbated matter for each shot should be implemented within an experimental setup. For example, laser radiation can be focused on a surface of a rapidly rotated cylinder[Reference Serbanescu, Fourmaux, Kieffer, Kincaid and Krol5]. But irradiation of such type targets is usually accompanied with all-direction debris dispersion which is undesirable within the context of the clean X-ray source creating. Other types of fast renewable targets are supersonic gas jets, gas clusters, liquid or hybrid structures. For all listed cases, repetition rate of X-ray pulses becomes limited only by laser pulses generation frequency.
${\sim}10^{19}~\text{W}/\text{cm}^{2}$ with frequency 0.1–10 Hz, but it implies special requirements for laser targets. A system which provides the interaction with non-perturbated matter for each shot should be implemented within an experimental setup. For example, laser radiation can be focused on a surface of a rapidly rotated cylinder[Reference Serbanescu, Fourmaux, Kieffer, Kincaid and Krol5]. But irradiation of such type targets is usually accompanied with all-direction debris dispersion which is undesirable within the context of the clean X-ray source creating. Other types of fast renewable targets are supersonic gas jets, gas clusters, liquid or hybrid structures. For all listed cases, repetition rate of X-ray pulses becomes limited only by laser pulses generation frequency.
An opportunity of liquid targets’ application, for example, of liquid gallium (Ga) was considered in Refs. [Reference Ivanov, Uryupina, Volkov, Shkurinov, Ozheredov, Paskhalov, Eremin and Savelev10–Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Kishimoto, Yamakawa, Faenov, Magunov, Pikuz, Skobelev, Abdallah, Csanak, Boldarev and Gasilov12]. This target is unique since it is completely renewable and makes the X-ray repetition rate depend only on the laser pulse repetition rate. Ga has an atomic number  $Z=31$ and it was enough to reach high X-ray photons yield about
$Z=31$ and it was enough to reach high X-ray photons yield about  $10^{5}$ photons/shot when liquid Ga target was irradiated by laser pulses with intensity
$10^{5}$ photons/shot when liquid Ga target was irradiated by laser pulses with intensity  ${\sim}2\times 10^{17}~\text{W}/\text{cm}^{2}$[Reference Ivanov, Uryupina, Volkov, Shkurinov, Ozheredov, Paskhalov, Eremin and Savelev10]. The main disadvantage of this target type is strong sputtering into vacuum space
${\sim}2\times 10^{17}~\text{W}/\text{cm}^{2}$[Reference Ivanov, Uryupina, Volkov, Shkurinov, Ozheredov, Paskhalov, Eremin and Savelev10]. The main disadvantage of this target type is strong sputtering into vacuum space  ${\sim}10^{3}~\unicode[STIX]{x03BC}\text{m}$ of liquid Ga per laser shot at laser intensity on target
${\sim}10^{3}~\unicode[STIX]{x03BC}\text{m}$ of liquid Ga per laser shot at laser intensity on target  ${\sim}10^{16}~\text{W}/\text{cm}^{2}$. High rate of an interaction volume pollution by small drops of liquid Ga makes it impossible to use this material as a target for experiments with even sub-relativistic laser pulses
${\sim}10^{16}~\text{W}/\text{cm}^{2}$. High rate of an interaction volume pollution by small drops of liquid Ga makes it impossible to use this material as a target for experiments with even sub-relativistic laser pulses  $(10^{16}\leqslant I_{\text{las}}\leqslant 10^{18}~\text{W}/\text{cm}^{2})$. Application of cluster targets allowed for obtaining rather high yield of X-ray photons[Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Kishimoto, Yamakawa, Faenov, Magunov, Pikuz, Skobelev, Abdallah, Csanak, Boldarev and Gasilov12–Reference Junkel-Vives, Abdallah, Auguste, D’Oliveira, Hulin, Monot, Dobosz, Faenov, Magunov, Pikuz, Skobelev, Boldarev and Gasilov14]. But in this case, depending on clusters formation conditions and type of a gas, laser-cluster plasma emits not only X-rays but also accelerated particles[Reference Parra, Alexeev, Fan, Kim, McNaught and Milchberg13–Reference Zhang, Chen, Wang, Yan, Yuan, Mao, Wang, Liu, Shen, Faenov, Pikuz, Li, Li, Dong, Lu, Ma, Wei, Sheng and Zhang17]. In Refs. [Reference Chen, Yan, Li, Hu, Zhang, Wang, Hafz, Mao, Huang, Ma, Zhao, Ma, Li, Lu, Sheng, Wei, Gao and Zhang2, Reference Zhang, Chen, Wang, Yan, Yuan, Mao, Wang, Liu, Shen, Faenov, Pikuz, Li, Li, Dong, Lu, Ma, Wei, Sheng and Zhang17, Reference Malka, Faure, Gauduel, Lefebvre, Rousse and Phuoc18] it was shown that intense laser pulses interaction with small-size clusters, i.e., in under-critical density area
$(10^{16}\leqslant I_{\text{las}}\leqslant 10^{18}~\text{W}/\text{cm}^{2})$. Application of cluster targets allowed for obtaining rather high yield of X-ray photons[Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Kishimoto, Yamakawa, Faenov, Magunov, Pikuz, Skobelev, Abdallah, Csanak, Boldarev and Gasilov12–Reference Junkel-Vives, Abdallah, Auguste, D’Oliveira, Hulin, Monot, Dobosz, Faenov, Magunov, Pikuz, Skobelev, Boldarev and Gasilov14]. But in this case, depending on clusters formation conditions and type of a gas, laser-cluster plasma emits not only X-rays but also accelerated particles[Reference Parra, Alexeev, Fan, Kim, McNaught and Milchberg13–Reference Zhang, Chen, Wang, Yan, Yuan, Mao, Wang, Liu, Shen, Faenov, Pikuz, Li, Li, Dong, Lu, Ma, Wei, Sheng and Zhang17]. In Refs. [Reference Chen, Yan, Li, Hu, Zhang, Wang, Hafz, Mao, Huang, Ma, Zhao, Ma, Li, Lu, Sheng, Wei, Gao and Zhang2, Reference Zhang, Chen, Wang, Yan, Yuan, Mao, Wang, Liu, Shen, Faenov, Pikuz, Li, Li, Dong, Lu, Ma, Wei, Sheng and Zhang17, Reference Malka, Faure, Gauduel, Lefebvre, Rousse and Phuoc18] it was shown that intense laser pulses interaction with small-size clusters, i.e., in under-critical density area  $(N<N_{\text{cr}}=10^{21}~\text{cm}^{-3})$, led to highly efficient wakefield acceleration of electrons up to energies
$(N<N_{\text{cr}}=10^{21}~\text{cm}^{-3})$, led to highly efficient wakefield acceleration of electrons up to energies  ${\sim}100~\text{MeV}$ in the laser propagation direction. Usage of big-size clusters with diameter
${\sim}100~\text{MeV}$ in the laser propagation direction. Usage of big-size clusters with diameter  $d\sim 1.5{-}3~\unicode[STIX]{x03BC}\text{m}$ results in successful formation of accelerated protons beams acquiring high energy as a result of Coulomb explosion of Ar clusters[Reference Tsymbalov, Ivanov, Volkov, Savel’ev, Novikov, Galanina, Chirskaya, Bychenkov and Chumakov11, Reference Malka, Faure, Gauduel, Lefebvre, Rousse and Phuoc18].
$d\sim 1.5{-}3~\unicode[STIX]{x03BC}\text{m}$ results in successful formation of accelerated protons beams acquiring high energy as a result of Coulomb explosion of Ar clusters[Reference Tsymbalov, Ivanov, Volkov, Savel’ev, Novikov, Galanina, Chirskaya, Bychenkov and Chumakov11, Reference Malka, Faure, Gauduel, Lefebvre, Rousse and Phuoc18].
Another approach of bright X-ray source creating is associated with hybrid targets which consist of a gas jet and a thick solid foil with  $Z>30$ located behind the jet. The idea of bright X-ray source formation by the application of hybrid targets is as follows. Laser pulse irradiates the gas jet and generates an underdense plasma, where electrons are accelerated up to MeV energies in the direction of laser propagation. These electrons collide with the thick solid foil which results in generation of intense bremsstrahlung emission. On the basis of theoretical calculations described in Ref. [Reference Compant La Fontaine, Courtois and Lefebvre19] it was shown that for such X-ray sources emission efficiency depends on the experimental conditions.
$Z>30$ located behind the jet. The idea of bright X-ray source formation by the application of hybrid targets is as follows. Laser pulse irradiates the gas jet and generates an underdense plasma, where electrons are accelerated up to MeV energies in the direction of laser propagation. These electrons collide with the thick solid foil which results in generation of intense bremsstrahlung emission. On the basis of theoretical calculations described in Ref. [Reference Compant La Fontaine, Courtois and Lefebvre19] it was shown that for such X-ray sources emission efficiency depends on the experimental conditions.
In this work we considered the simplest type of target structure – gas jets with molecular density  ${\sim}10^{17}{-}10^{18}~\text{cm}^{-3}$, injected from a nozzle under the pressure about several MPa. Commonly, molecular gases are used as targets: oxygen
${\sim}10^{17}{-}10^{18}~\text{cm}^{-3}$, injected from a nozzle under the pressure about several MPa. Commonly, molecular gases are used as targets: oxygen  $(\text{O}_{2})$, nitrogen
$(\text{O}_{2})$, nitrogen  $(\text{N}_{2})$, hydrogen
$(\text{N}_{2})$, hydrogen  $(\text{H}_{2})$, carbon dioxide
$(\text{H}_{2})$, carbon dioxide  $(\text{CO}_{2})$ or molecular gases (
$(\text{CO}_{2})$ or molecular gases ( $\text{SF}_{6}$,
$\text{SF}_{6}$,  $\text{CF}_{3}\text{I}$)[Reference Gordienko, Djidjoev, Zhvaniya, Petukhov, Platonenko, Trubnikov and Khomenko20, Reference Gordienko, Dzhidzhoev, Zhvaniya, Platonenko, Trubnikov and Fedorov21]; and also atomic gases: helium (He,
$\text{CF}_{3}\text{I}$)[Reference Gordienko, Djidjoev, Zhvaniya, Petukhov, Platonenko, Trubnikov and Khomenko20, Reference Gordienko, Dzhidzhoev, Zhvaniya, Platonenko, Trubnikov and Fedorov21]; and also atomic gases: helium (He,  $Z=2$), neon (Ne,
$Z=2$), neon (Ne,  $Z=10$), argon (Ar,
$Z=10$), argon (Ar,  $Z=18$), xenon (Xe,
$Z=18$), xenon (Xe,  $Z=36$) and krypton (Kr,
$Z=36$) and krypton (Kr,  $Z=54$). It is admittedly known that generation of fast ions and neutron beams does not happen in the case of laser interaction with a gas jet target. Thus, there is an opportunity to find such experimental conditions when efficiency of electron acceleration process is rather low, but emission of soft X-ray radiation is quite intense. It is possible to vary such parameters of a gas jet as gas type, gas jet density (inlet pressure of a nozzle), and volume (size) of interaction area in the direction of laser pulse propagation (i.e., laser beam focusing). Parameters of X-ray emission source depend on experimental setup geometry and main laser pulse parameters: laser pulse energy –
$Z=54$). It is admittedly known that generation of fast ions and neutron beams does not happen in the case of laser interaction with a gas jet target. Thus, there is an opportunity to find such experimental conditions when efficiency of electron acceleration process is rather low, but emission of soft X-ray radiation is quite intense. It is possible to vary such parameters of a gas jet as gas type, gas jet density (inlet pressure of a nozzle), and volume (size) of interaction area in the direction of laser pulse propagation (i.e., laser beam focusing). Parameters of X-ray emission source depend on experimental setup geometry and main laser pulse parameters: laser pulse energy –  $E_{\text{las}}$, laser pulse duration –
$E_{\text{las}}$, laser pulse duration –  $\unicode[STIX]{x1D70F}_{\text{las}}$, laser intensity on a target –
$\unicode[STIX]{x1D70F}_{\text{las}}$, laser intensity on a target –  $I_{\text{las}}$ and laser pulse contrast (intensity ratio of the main laser pulse to the laser prepulse) –
$I_{\text{las}}$ and laser pulse contrast (intensity ratio of the main laser pulse to the laser prepulse) –  $K_{\text{las}}$. From the point of view of X-ray emission yield increase, theoretical statements demand to use targets made of high
$K_{\text{las}}$. From the point of view of X-ray emission yield increase, theoretical statements demand to use targets made of high  $Z$ materials. In the gas jet case, it mostly implies application of noble gases: argon, xenon, krypton. Usage of heavy gases (for example, Xe with
$Z$ materials. In the gas jet case, it mostly implies application of noble gases: argon, xenon, krypton. Usage of heavy gases (for example, Xe with  $Z=36$ and Kr with
$Z=36$ and Kr with  $Z=54$) as a target requires laser intensities up to
$Z=54$) as a target requires laser intensities up to  $10^{20}~\text{W}/\text{cm}^{2}$. Even though such laser systems are widely used in laboratories around the world, they are still ‘unique’ and not mass produced. In turn, laser systems capable to generate femtosecond laser pulses with an intensity of
$10^{20}~\text{W}/\text{cm}^{2}$. Even though such laser systems are widely used in laboratories around the world, they are still ‘unique’ and not mass produced. In turn, laser systems capable to generate femtosecond laser pulses with an intensity of  $I_{\text{las}}\sim 10^{16}{-}10^{19}~\text{W}/\text{cm}^{2}$ on a target have already become commercially available (see, for example, Ref. [22]), compact facilities that are orders of magnitude cheaper than such sources of soft X-ray radiation as X-ray free electron lasers or synchrotron acceleration facilities.
$I_{\text{las}}\sim 10^{16}{-}10^{19}~\text{W}/\text{cm}^{2}$ on a target have already become commercially available (see, for example, Ref. [22]), compact facilities that are orders of magnitude cheaper than such sources of soft X-ray radiation as X-ray free electron lasers or synchrotron acceleration facilities.
This paper is devoted to investigation of optimal conditions for clean X-ray source formation in plasma, generated by high-contrast  $({\sim}10^{9})$ relativistic
$({\sim}10^{9})$ relativistic  $(I_{\text{las}}\sim 10^{16}{-}10^{19}~\text{W}/\text{cm}^{2})$ femtosecond laser pulses interaction with argon
$(I_{\text{las}}\sim 10^{16}{-}10^{19}~\text{W}/\text{cm}^{2})$ femtosecond laser pulses interaction with argon  $(Z=18)$ gas jets. The search of optimal conditions was done by X-ray spectroscopy approaches, allowing for measuring main parameters of the plasma source and its X-ray emission efficiency.
$(Z=18)$ gas jets. The search of optimal conditions was done by X-ray spectroscopy approaches, allowing for measuring main parameters of the plasma source and its X-ray emission efficiency.

Figure 1. (a) General scheme of the experimental setup. (b) Central cross-section of the nozzle. (c) Coordinates of the focal spot position.
2 Experimental setup
The experiments were performed on the laser facility IOP 20 TW at the Institute of Physics (IOP), Chinese Academy of Sciences[22, Reference Wang, Feng, Zhu, Li, He, Li, Tan, Ma and Chen23]. This Ti:sapphire laser, operated by the chirped-pulse amplification scheme is capable of generating high-contrast  $K_{\text{las}}\sim 10^{9}$ (laser contrast measured at picosecond scale) laser pulses at
$K_{\text{las}}\sim 10^{9}$ (laser contrast measured at picosecond scale) laser pulses at  $\unicode[STIX]{x1D706}=800~\text{nm}$ wavelength (full width at half maximum) with energy up to
$\unicode[STIX]{x1D706}=800~\text{nm}$ wavelength (full width at half maximum) with energy up to  $E_{\text{las}}\sim 500~\text{mJ}$ per pulse and duration of
$E_{\text{las}}\sim 500~\text{mJ}$ per pulse and duration of  $\unicode[STIX]{x1D70F}_{\text{las}}\sim 40~\text{fs}$. A laser beam with diameter
$\unicode[STIX]{x1D70F}_{\text{las}}\sim 40~\text{fs}$. A laser beam with diameter  ${\sim}5~\text{cm}$ was focused by an off-axis parabolic mirror with f-number 3.5 to form a focal spot with diameter
${\sim}5~\text{cm}$ was focused by an off-axis parabolic mirror with f-number 3.5 to form a focal spot with diameter  $d\sim 5~\unicode[STIX]{x03BC}\text{m}$, that corresponds to the laser intensity on a target up to
$d\sim 5~\unicode[STIX]{x03BC}\text{m}$, that corresponds to the laser intensity on a target up to  $I_{\text{lt}}\sim 2\times 10^{19}~\text{W}/\text{cm}^{2}$. A supersonic Ar gas jet was formed by a slit nozzle (named as wave-free supersonic slit nozzle MS05-10-166[Reference Hosokai, Kinoshita, Watanabe, Yoshii, Ueda, Zhidokov, Uesaka, Nakajima, Kando, Kotaki and Kansai24] by SourceLAB) with a rectangular slit profile with width 1.2 mm and length 5 mm. The laser beam was focused at the center of the gas jet (distance from the edge of the nozzle outlet
$I_{\text{lt}}\sim 2\times 10^{19}~\text{W}/\text{cm}^{2}$. A supersonic Ar gas jet was formed by a slit nozzle (named as wave-free supersonic slit nozzle MS05-10-166[Reference Hosokai, Kinoshita, Watanabe, Yoshii, Ueda, Zhidokov, Uesaka, Nakajima, Kando, Kotaki and Kansai24] by SourceLAB) with a rectangular slit profile with width 1.2 mm and length 5 mm. The laser beam was focused at the center of the gas jet (distance from the edge of the nozzle outlet  $L_{x}=0.6~\text{mm}$) parallel to the short edge of the nozzle (see Figure 1).
$L_{x}=0.6~\text{mm}$) parallel to the short edge of the nozzle (see Figure 1).
Distance from the nozzle outlet to focal spot position along a gas spread axis  $(L_{z})$ was varied from 1 to 4 mm. The Ar gas inlet pressure range was:
$(L_{z})$ was varied from 1 to 4 mm. The Ar gas inlet pressure range was:  $P_{\text{gas}}=2{-}9~\text{MPa}$. Recently[Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25] it was shown that Ar gas jets created by the mentioned nozzle contains a significant amount of nm-size Ar clusters. We carried out simulations of cluster formation for our conditions on the basis of the model described in Ref. [Reference Boldarev, Gasilov, Faenov, Fukuda and Yamakawa26]. The calculations demonstrate that for the inlet pressure of 6 MPa and
$P_{\text{gas}}=2{-}9~\text{MPa}$. Recently[Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25] it was shown that Ar gas jets created by the mentioned nozzle contains a significant amount of nm-size Ar clusters. We carried out simulations of cluster formation for our conditions on the basis of the model described in Ref. [Reference Boldarev, Gasilov, Faenov, Fukuda and Yamakawa26]. The calculations demonstrate that for the inlet pressure of 6 MPa and  $L_{z}=1~\text{mm}$ cluster concentration reached
$L_{z}=1~\text{mm}$ cluster concentration reached  $5\times 10^{12}~\text{cm}^{-3}$, gas atomic density
$5\times 10^{12}~\text{cm}^{-3}$, gas atomic density  ${\sim}5\times 10^{19}~\text{cm}^{-3}$ and radius of cluster
${\sim}5\times 10^{19}~\text{cm}^{-3}$ and radius of cluster  ${\sim}25~\text{nm}$. However, such clusters are very small and are destroyed already by a laser prepulse even with intensity
${\sim}25~\text{nm}$. However, such clusters are very small and are destroyed already by a laser prepulse even with intensity  ${\sim}10^{10}~\text{W}/\text{cm}^{2}$. Thus, in our case the main laser pulse interacts only with Ar gas and existence of insufficient amount of Ar clusters in the jet did not influence investigated laser–gas jet interaction processes.
${\sim}10^{10}~\text{W}/\text{cm}^{2}$. Thus, in our case the main laser pulse interacts only with Ar gas and existence of insufficient amount of Ar clusters in the jet did not influence investigated laser–gas jet interaction processes.

Figure 2. (a), (b) X-ray emission spectra and (c)–(e) corresponding electron measurement results detected in  $0^{\circ }$-direction (laser propagation axis) for the following experimental conditions: inlet gas pressure –
$0^{\circ }$-direction (laser propagation axis) for the following experimental conditions: inlet gas pressure –  $P_{\text{gas}}=6~\text{MPa}$, laser energy –
$P_{\text{gas}}=6~\text{MPa}$, laser energy –  $E_{\text{las}}=250~\text{mJ}$, laser beam is focused at the center of Ar gas jet, perpendicularly to gas flow
$E_{\text{las}}=250~\text{mJ}$, laser beam is focused at the center of Ar gas jet, perpendicularly to gas flow  $z$-axis at the distance from nozzle outlet (a), (c), (d)
$z$-axis at the distance from nozzle outlet (a), (c), (d)  $L_{z}=1~\text{mm}$ and (b), (e)
$L_{z}=1~\text{mm}$ and (b), (e)  $L_{z}=2~\text{mm}$.
$L_{z}=2~\text{mm}$.
The X-ray radiation of the plasma, generated during the laser pulses interaction with the Ar gas jet, was detected by three focusing spectrometers with high spatial resolution (FSSRs)[Reference Faenov, Pikuz, Erko, Bryunetkin, Dyakin, Ivanenkov, Mingaleev, Pikuz, Romanova and Shelkovenko27, Reference Skobelev, Faenov, Bryunetkin, Dyakin, Pikuz, Pikuz, Shelkovenko, Romanova and Mingaleev28] equipped by spherically bent crystals of  $\unicode[STIX]{x1D6FC}$-quartz with curvature radius
$\unicode[STIX]{x1D6FC}$-quartz with curvature radius  $R=150~\text{mm}$ (see Figure 1). The spectrometers were aligned to observe X-rays emitted in three different directions: FSSR-
$R=150~\text{mm}$ (see Figure 1). The spectrometers were aligned to observe X-rays emitted in three different directions: FSSR- $0^{\circ }$ – the direction of laser propagation we choose as the zero-degree direction (
$0^{\circ }$ – the direction of laser propagation we choose as the zero-degree direction ( $0^{\circ }$-direction below), FSSR-
$0^{\circ }$-direction below), FSSR- $45^{\circ }$ – the direction at an angle of
$45^{\circ }$ – the direction at an angle of  $45^{\circ }$ to the laser propagation axis; and FSSR-
$45^{\circ }$ to the laser propagation axis; and FSSR- $90^{\circ }$ – perpendicular to the laser propagation axis. The spectrometer FSSR-
$90^{\circ }$ – perpendicular to the laser propagation axis. The spectrometer FSSR- $0^{\circ }$ was equipped by the spherically bent
$0^{\circ }$ was equipped by the spherically bent  $\unicode[STIX]{x1D6FC}$-quartz crystal with the Miller indices 22(-4)3 (lattice space –
$\unicode[STIX]{x1D6FC}$-quartz crystal with the Miller indices 22(-4)3 (lattice space –  $2d=4.91~\text{Å}$) and located 10.5 cm higher than interaction plane at the distance
$2d=4.91~\text{Å}$) and located 10.5 cm higher than interaction plane at the distance  $a=374.4~\text{mm}$ from the laser focusing point. This spectrometer was aligned to FSSR-I mode when an X-ray detector is also located on the Rowland circle and spectral resolution of scheme does not depend on emission source size. Thereby, FSSR-
$a=374.4~\text{mm}$ from the laser focusing point. This spectrometer was aligned to FSSR-I mode when an X-ray detector is also located on the Rowland circle and spectral resolution of scheme does not depend on emission source size. Thereby, FSSR- $0^{\circ }$ registered X-ray emission in the wavelength range
$0^{\circ }$ registered X-ray emission in the wavelength range  $\unicode[STIX]{x1D706}=3.7{-}4.25~\text{Å}$. The spectrometers FSSR-
$\unicode[STIX]{x1D706}=3.7{-}4.25~\text{Å}$. The spectrometers FSSR- $0^{\circ }$ and FSSR-
$0^{\circ }$ and FSSR- $90^{\circ }$ were equipped by identical bent
$90^{\circ }$ were equipped by identical bent  $\unicode[STIX]{x1D6FC}$-quartz crystals 11(-2)0 (
$\unicode[STIX]{x1D6FC}$-quartz crystals 11(-2)0 ( $2d=6.66~\text{Å}$) and located directly in the interaction plane at the distance
$2d=6.66~\text{Å}$) and located directly in the interaction plane at the distance  $a=400~\text{mm}$ from the laser focusing point. Both spectrometers were used at FSSR-II mode and provided X-ray emission measurements with spatial resolution along the laser propagation axis (FSSR-
$a=400~\text{mm}$ from the laser focusing point. Both spectrometers were used at FSSR-II mode and provided X-ray emission measurements with spatial resolution along the laser propagation axis (FSSR- $90^{\circ }$) and along gas jet propagation (FSSR-
$90^{\circ }$) and along gas jet propagation (FSSR- $45^{\circ }$). For the FSSR-
$45^{\circ }$). For the FSSR- $45^{\circ }$ and FSSR-
$45^{\circ }$ and FSSR- $90^{\circ }$ a central wavelength was chosen as
$90^{\circ }$ a central wavelength was chosen as  $\unicode[STIX]{x1D706}_{0}=4~\text{Å}$ to provide the detection range
$\unicode[STIX]{x1D706}_{0}=4~\text{Å}$ to provide the detection range  $\unicode[STIX]{x1D706}=3.2{-}4.5~\text{Å}$. We used Fujifilm BAS TR Image Plates as X-ray detectors. The plates were scanned by the Amersham Typhoon FLA scanner by General Electric with the pixel size of
$\unicode[STIX]{x1D706}=3.2{-}4.5~\text{Å}$. We used Fujifilm BAS TR Image Plates as X-ray detectors. The plates were scanned by the Amersham Typhoon FLA scanner by General Electric with the pixel size of  $25~\unicode[STIX]{x03BC}\text{m}$. The detectors were protected against exposure of the visible light by two layers of
$25~\unicode[STIX]{x03BC}\text{m}$. The detectors were protected against exposure of the visible light by two layers of  $1~\unicode[STIX]{x03BC}\text{m}$ thick polypropylene coated by
$1~\unicode[STIX]{x03BC}\text{m}$ thick polypropylene coated by  $0.2~\unicode[STIX]{x03BC}\text{m}$ Al. The X-ray emission spectra were measured at cumulative mode: one spectrum for 50 laser flashing with frequency 0.3 Hz.
$0.2~\unicode[STIX]{x03BC}\text{m}$ Al. The X-ray emission spectra were measured at cumulative mode: one spectrum for 50 laser flashing with frequency 0.3 Hz.

Figure 3. X-ray emission spectra of Ar plasma depend on  $L_{z}$ – laser focusing point displacement from nozzle outlet
$L_{z}$ – laser focusing point displacement from nozzle outlet  $(L_{z}=2{-}4~\text{mm})$, measured at fixed parameters: inlet Ar gas pressure –
$(L_{z}=2{-}4~\text{mm})$, measured at fixed parameters: inlet Ar gas pressure –  $P_{\text{gas}}=6~\text{MPa}$, laser energy on target –
$P_{\text{gas}}=6~\text{MPa}$, laser energy on target –  $E_{\text{las}}=250~\text{mJ}$, laser pulse duration –
$E_{\text{las}}=250~\text{mJ}$, laser pulse duration –  $\unicode[STIX]{x1D70F}_{\text{las}}\sim 45~\text{fs}$, laser contrast –
$\unicode[STIX]{x1D70F}_{\text{las}}\sim 45~\text{fs}$, laser contrast –  $K_{\text{las}}\sim 10^{9}$ in diagnostic direction (a)
$K_{\text{las}}\sim 10^{9}$ in diagnostic direction (a)  $0^{\circ }$, (b)
$0^{\circ }$, (b)  $45^{\circ }$ and (c)
$45^{\circ }$ and (c)  $90^{\circ }$. Note that, the X-ray intensity on axis of ordinates is given in absolute values.
$90^{\circ }$. Note that, the X-ray intensity on axis of ordinates is given in absolute values.
Response functions for all diagnostic equipment included in the spectrometric route were considered step by step to calculate absolute values of spectral lines’ intensities from raw data. First, values of a raw grayscale image produced by the scanner can be easily recalculated to photostimulated luminescence (PSL) units according to manufacturer specifications described for example in Ref. [Reference Haugh, Lee, Romano and Schneider29]. The PSL values are linearly[Reference Holder, Izumi, Beach, Ayers, Bell, Schneider, Bradley, Kohut, Ehrlich, Cohen, Ramirez and Thorn30] proportional to incident photon energy for soft (at least for photon energy  ${<}20~\text{keV}$) X-rays. These two facts together allow for obtaining exact number of photons per image plate pixel. This number also should be corrected according to transmission functions of filters which were placed in front of the image plates to protect them from visible light. The X-ray transmission properties for a variety of different materials can be obtained, for example, from the Henke database[Reference Henke, Gullikson and Davis31]. Also, the crystal reflectivity efficiency should be considered. It differs for different wavelengths of the incident radiation. Ray-tracing computer simulations described in Ref. [Reference Lavrinenko, Morozov, Pikuz and Skobelev32] were performed to study reflectivity properties of the crystals used for the measurements. In the simulations the real shape of rocking curve for different wavelengths was included. The curve shape was calculated by the XOP software[Reference Sánchez del Río and Dejus33]. Also, a solid angle of the dispersive crystal was calculated according to experimental geometry to estimate a fraction of photons which miss a crystal surface.
${<}20~\text{keV}$) X-rays. These two facts together allow for obtaining exact number of photons per image plate pixel. This number also should be corrected according to transmission functions of filters which were placed in front of the image plates to protect them from visible light. The X-ray transmission properties for a variety of different materials can be obtained, for example, from the Henke database[Reference Henke, Gullikson and Davis31]. Also, the crystal reflectivity efficiency should be considered. It differs for different wavelengths of the incident radiation. Ray-tracing computer simulations described in Ref. [Reference Lavrinenko, Morozov, Pikuz and Skobelev32] were performed to study reflectivity properties of the crystals used for the measurements. In the simulations the real shape of rocking curve for different wavelengths was included. The curve shape was calculated by the XOP software[Reference Sánchez del Río and Dejus33]. Also, a solid angle of the dispersive crystal was calculated according to experimental geometry to estimate a fraction of photons which miss a crystal surface.
For measurements of electron energy distribution, we used a split electron spectrometer with magnetic field  $B=9000~\text{G}$. The e-spectrometer was equipped by photoluminescent plates Fujifilm-MS (scanning pixel size –
$B=9000~\text{G}$. The e-spectrometer was equipped by photoluminescent plates Fujifilm-MS (scanning pixel size –  $d_{\text{pix}}=50~\unicode[STIX]{x03BC}\text{m}$) for electron signal detection. The e-spectrometer was installed in the interaction plane at the distance
$d_{\text{pix}}=50~\unicode[STIX]{x03BC}\text{m}$) for electron signal detection. The e-spectrometer was installed in the interaction plane at the distance  ${\sim}20~\text{cm}$ from the focusing point. It was aligned to detect emission of fast electrons in the energy range 10–120 MeV in the direction of laser propagation axis (
${\sim}20~\text{cm}$ from the focusing point. It was aligned to detect emission of fast electrons in the energy range 10–120 MeV in the direction of laser propagation axis ( $0^{\circ }$-direction). We also provided monitoring of an electron beam profile and estimating of its energy distribution in a low-energy range (few keV) via image plates Fujifilm-MS covered by 1–5 layers of Al foils with thickness
$0^{\circ }$-direction). We also provided monitoring of an electron beam profile and estimating of its energy distribution in a low-energy range (few keV) via image plates Fujifilm-MS covered by 1–5 layers of Al foils with thickness  $15~\unicode[STIX]{x03BC}\text{m}$. These image plates were located in
$15~\unicode[STIX]{x03BC}\text{m}$. These image plates were located in  $0^{\circ }$-direction in the interaction plane
$0^{\circ }$-direction in the interaction plane  ${\sim}20~\text{cm}$ far from the focusing point on a front surface of the e-spectrometer and had an orifice for passing electrons inside the spectrometer.
${\sim}20~\text{cm}$ far from the focusing point on a front surface of the e-spectrometer and had an orifice for passing electrons inside the spectrometer.
3 Results and discussion
For the search of optimal conditions for generation of the clean X-ray source in relativistic laser-produced plasma, first we must choose the initial experimental parameters for following the search step by step. The important challenge was the choice of laser focusing geometry, i.e., which region of the gas jet should be chosen as a laser focusing point. In some previous papers devoted to electron acceleration it was shown that a laser beam normally focused on a far wall of a gas jet and the distance from a nozzle exit plane was about 0.5–1 mm [Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Skobelev, Faenov, Bryunetkin, Dyakin, Pikuz, Pikuz, Shelkovenko, Romanova and Mingaleev28, Reference Zhang, Chen, Yuan, Yan, Wang, Liu, Shen, Faenov, Pikuz, Skobelev, Gasilov, Boldarev, Mao, Li, Dong, Lu, Ma, Wang, Sheng and Zhang34, Reference Koester, Bussolino, Cristoforetti, Faenov, Giulietti, Giulietti, Labate, Levato, Pikuz and Gizzi35]. Typical inlet Ar gas pressure was about 4–5 MPa [Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Zhang, Chen, Yuan, Yan, Wang, Liu, Shen, Faenov, Pikuz, Skobelev, Gasilov, Boldarev, Mao, Li, Dong, Lu, Ma, Wang, Sheng and Zhang34]. To avoid the experimental conditions when electrons are accelerated up to MeV energies with high efficiency, we chose the following initial conditions: inlet Ar pressure  $P_{\text{gas}}=6~\text{MPa}$, laser beam focused at the center of the gas jet at the distance from the nozzle outlet
$P_{\text{gas}}=6~\text{MPa}$, laser beam focused at the center of the gas jet at the distance from the nozzle outlet  $L_{z}\geqslant 1~\text{mm}$. X-ray emission spectra of Ar plasma detected for these experimental conditions by FSSR-
$L_{z}\geqslant 1~\text{mm}$. X-ray emission spectra of Ar plasma detected for these experimental conditions by FSSR- $0^{\circ }$ and typical spectrograms are shown in Figure 2(a).
$0^{\circ }$ and typical spectrograms are shown in Figure 2(a).
As it is seen from Figure 2(a), the detector surface was brightened by a uniform noisy signal. The faint signal on the associated spectrum corresponds to resonant line of  $\text{He}_{\unicode[STIX]{x1D6FC}1}$ and intercombination line
$\text{He}_{\unicode[STIX]{x1D6FC}1}$ and intercombination line  $\text{He}_{\unicode[STIX]{x1D6FC}2}$ corresponding to transitions in helium-like argon ions Ar XVII. The uniform background we observed on the X-ray detector appeared due to polychromatic high intensity emission produced by MeV-electrons effectively accelerated during the laser–gas interaction. The energy distribution of such electrons is shown in Figure 2(c) and the shape of the electron beam on the distance 20 cm far from the source is shown in Figure 2(d). It demonstrates that in the case of initial experimental condition described above, the most part of laser energy is spent on the electron acceleration with middle energy
$\text{He}_{\unicode[STIX]{x1D6FC}2}$ corresponding to transitions in helium-like argon ions Ar XVII. The uniform background we observed on the X-ray detector appeared due to polychromatic high intensity emission produced by MeV-electrons effectively accelerated during the laser–gas interaction. The energy distribution of such electrons is shown in Figure 2(c) and the shape of the electron beam on the distance 20 cm far from the source is shown in Figure 2(d). It demonstrates that in the case of initial experimental condition described above, the most part of laser energy is spent on the electron acceleration with middle energy  ${\sim}20~\text{MeV}$, which did not fulfill the goal of clean X-ray source formation.
${\sim}20~\text{MeV}$, which did not fulfill the goal of clean X-ray source formation.

Figure 4. (a) Dependence of the X-ray emission registered in the  $90^{\circ }$-direction on
$90^{\circ }$-direction on  $L_{z}$ (the distance from the nozzle outlet to the laser focusing point). Simulated spectra obtained by the radiational–collisional code PrismSpect for different electron temperatures
$L_{z}$ (the distance from the nozzle outlet to the laser focusing point). Simulated spectra obtained by the radiational–collisional code PrismSpect for different electron temperatures  $T_{\text{e}}$, fixed atomic densities and the hot electrons fraction of 0.1% with the temperature
$T_{\text{e}}$, fixed atomic densities and the hot electrons fraction of 0.1% with the temperature  $T_{\text{hot}}=3~\text{keV}$ are shown by the red lines. (b) X-ray yield per laser shot of photons with the energy of
$T_{\text{hot}}=3~\text{keV}$ are shown by the red lines. (b) X-ray yield per laser shot of photons with the energy of  $E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ versus distance from the nozzle throat
$E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ versus distance from the nozzle throat  $(L_{z})$ for diagnostic directions
$(L_{z})$ for diagnostic directions  $0^{\circ }$,
$0^{\circ }$,  $45^{\circ }$ and
$45^{\circ }$ and  $90^{\circ }$. (c) Results of hydrodynamic calculations for the gas jet density profile for the slit nozzle MS05-10-166[Reference Hosokai, Kinoshita, Watanabe, Yoshii, Ueda, Zhidokov, Uesaka, Nakajima, Kando, Kotaki and Kansai24] and different
$90^{\circ }$. (c) Results of hydrodynamic calculations for the gas jet density profile for the slit nozzle MS05-10-166[Reference Hosokai, Kinoshita, Watanabe, Yoshii, Ueda, Zhidokov, Uesaka, Nakajima, Kando, Kotaki and Kansai24] and different  $L_{z}$.
$L_{z}$.
Displacement of the focusing point 2 mm higher from the nozzle outlet, at the position  $L_{z}=2~\text{mm}$, with keeping other experimental parameters, has led to an interesting result (see Figure 2(b)). At this focusing geometry the X-ray detector surface remained clean, with a negligible level of the noise signal. The spectrogram shows the absence of intense noise background and contains only X-ray emission signal – spectral lines corresponding to transitions in He, Li-, Be-, B-like ions of argon. The signal on the e-spectrometer also disappeared, but on the image plate installed in front of the e-spectrometer in
$L_{z}=2~\text{mm}$, with keeping other experimental parameters, has led to an interesting result (see Figure 2(b)). At this focusing geometry the X-ray detector surface remained clean, with a negligible level of the noise signal. The spectrogram shows the absence of intense noise background and contains only X-ray emission signal – spectral lines corresponding to transitions in He, Li-, Be-, B-like ions of argon. The signal on the e-spectrometer also disappeared, but on the image plate installed in front of the e-spectrometer in  $0^{\circ }$-direction we observed a spatial profile of electron beams deflected by edge magnetic fields (see Figure 2(e)). The electrons energy estimated using Larmor radius equation for electron in magnetic field does not exceed 0.3 MeV. X-ray emission spectra of the Ar plasma measured for diagnostic directions,
$0^{\circ }$-direction we observed a spatial profile of electron beams deflected by edge magnetic fields (see Figure 2(e)). The electrons energy estimated using Larmor radius equation for electron in magnetic field does not exceed 0.3 MeV. X-ray emission spectra of the Ar plasma measured for diagnostic directions,  $0^{\circ }$,
$0^{\circ }$,  $45^{\circ }$ and
$45^{\circ }$ and  $90^{\circ }$, for different
$90^{\circ }$, for different  $L_{z}$ distances
$L_{z}$ distances  $(L_{z}=2{-}4~\text{mm})$ from the nozzle outlet, are shown in Figure 3. Using the spectra measured at FSSR-II mode,
$(L_{z}=2{-}4~\text{mm})$ from the nozzle outlet, are shown in Figure 3. Using the spectra measured at FSSR-II mode,  $90^{\circ }$-direction, a typical scale length of the source was estimated as
$90^{\circ }$-direction, a typical scale length of the source was estimated as  ${\sim}250~\unicode[STIX]{x03BC}\text{m}$.
${\sim}250~\unicode[STIX]{x03BC}\text{m}$.
Figure 3 demonstrates that shifting up of the laser focusing point along the gas jet expansion axis notably changes the X-ray emission spectral shape. The intensive resonant line –  $\text{He}_{\unicode[STIX]{x1D6FC}1}$ and intercombination line –
$\text{He}_{\unicode[STIX]{x1D6FC}1}$ and intercombination line –  $\text{He}_{\unicode[STIX]{x1D6FC}2}$ of Ar XVII simultaneously with lines of Li- and Be-like satellites were observed for
$\text{He}_{\unicode[STIX]{x1D6FC}2}$ of Ar XVII simultaneously with lines of Li- and Be-like satellites were observed for  $L_{z}=2~\text{mm}$. Spectral lines corresponding to B-, C- and N-like argon ions appeared on the spectra for higher
$L_{z}=2~\text{mm}$. Spectral lines corresponding to B-, C- and N-like argon ions appeared on the spectra for higher  $L_{z}$ and relative intensity of these lines gradually increased. For the fixed laser pulse parameters (
$L_{z}$ and relative intensity of these lines gradually increased. For the fixed laser pulse parameters ( $E_{\text{las}}=250~\text{mJ}$,
$E_{\text{las}}=250~\text{mJ}$,  $\unicode[STIX]{x1D70F}_{\text{las}}\sim 45~\text{fs}$,
$\unicode[STIX]{x1D70F}_{\text{las}}\sim 45~\text{fs}$,  $I_{\text{lt}}\sim 2\times 10^{19}~\text{W}/\text{cm}^{2}$,
$I_{\text{lt}}\sim 2\times 10^{19}~\text{W}/\text{cm}^{2}$,  $K_{\text{las}}\sim 10^{9}$), such spectral changes should be evidently associated both with decreasing of the gas jet density along the
$K_{\text{las}}\sim 10^{9}$), such spectral changes should be evidently associated both with decreasing of the gas jet density along the  $z$-axis and different plasma temperatures.
$z$-axis and different plasma temperatures.

Figure 5. Dependence of Ar plasma X-ray emission spectra on the laser pulse energy  $E_{\text{las}}=50{-}280~\text{mJ}$. The X-ray emission was observed in (a)
$E_{\text{las}}=50{-}280~\text{mJ}$. The X-ray emission was observed in (a)  $0^{\circ }$-direction, (b)
$0^{\circ }$-direction, (b)  $45^{\circ }$-direction and (c)
$45^{\circ }$-direction and (c)  $90^{\circ }$-direction. The X-ray emission spectra have been measured under the following experimental conditions: entry pressure of the Ar gas jet –
$90^{\circ }$-direction. The X-ray emission spectra have been measured under the following experimental conditions: entry pressure of the Ar gas jet –  $P_{\text{gas}}=6~\text{MPa}$, the distance from nozzle outlet to laser focus position –
$P_{\text{gas}}=6~\text{MPa}$, the distance from nozzle outlet to laser focus position –  $L_{z}=2~\text{mm}$, laser pulse duration –
$L_{z}=2~\text{mm}$, laser pulse duration –  $\unicode[STIX]{x1D70F}_{\text{las}}=45~\text{fs}$, laser pulse contrast –
$\unicode[STIX]{x1D70F}_{\text{las}}=45~\text{fs}$, laser pulse contrast –  $K_{\text{las}}=10^{9}$.
$K_{\text{las}}=10^{9}$.
Figure 4 shows the comparison between X-ray spectra measured in the  $90^{\circ }$-direction and kinetic modeling carried out with collisional-radiative computational code PrismSpect[Reference MacFarlane, Golovkin, Woodruff, Kulkarni and Hall36]. Since the gas density changes only for 2.5 times with shifting from
$90^{\circ }$-direction and kinetic modeling carried out with collisional-radiative computational code PrismSpect[Reference MacFarlane, Golovkin, Woodruff, Kulkarni and Hall36]. Since the gas density changes only for 2.5 times with shifting from  $L_{z}=1~\text{mm}$ to
$L_{z}=1~\text{mm}$ to  $L_{z}=2~\text{mm}$ (see Figure 4(c)), the calculations have been done for various values of plasma electron temperature in the assumption of zero optical depth for the fixed atomic densities
$L_{z}=2~\text{mm}$ (see Figure 4(c)), the calculations have been done for various values of plasma electron temperature in the assumption of zero optical depth for the fixed atomic densities  $N_{\text{i}}=5.2~\times 10^{19}{-}2.1\times 10^{19}~\text{cm}^{-3}$ for various
$N_{\text{i}}=5.2~\times 10^{19}{-}2.1\times 10^{19}~\text{cm}^{-3}$ for various  $L_{z}=1{-}4~\text{mm}$ and a hot electrons fraction 0.1% with the temperature 3 keV. Reached good correspondence of the measured and calculated spectra allowed for asserting that when the distance
$L_{z}=1{-}4~\text{mm}$ and a hot electrons fraction 0.1% with the temperature 3 keV. Reached good correspondence of the measured and calculated spectra allowed for asserting that when the distance  $L_{z}$ is varied from 1 to 2 mm the plasma electron temperature remained
$L_{z}$ is varied from 1 to 2 mm the plasma electron temperature remained  $T_{\text{e}}=180~(\pm 5)~\text{eV}$, but following distance increase
$T_{\text{e}}=180~(\pm 5)~\text{eV}$, but following distance increase  $L_{z}\geqslant 2~\text{mm}$ resulted in decreasing of electron temperature by 40 eV. Consequently, it also led to the X-ray emission intensity decrease by more than one order of magnitude. Numerical estimations for the number of X-ray photons –
$L_{z}\geqslant 2~\text{mm}$ resulted in decreasing of electron temperature by 40 eV. Consequently, it also led to the X-ray emission intensity decrease by more than one order of magnitude. Numerical estimations for the number of X-ray photons –  $\unicode[STIX]{x1D702}_{\text{ph}}$ emitted from the argon plasma within the full solid angle for one laser shot were obtained by integrating the experimentally measured spectra (see Figure 3) over the wavelength range
$\unicode[STIX]{x1D702}_{\text{ph}}$ emitted from the argon plasma within the full solid angle for one laser shot were obtained by integrating the experimentally measured spectra (see Figure 3) over the wavelength range  $\unicode[STIX]{x1D706}=3.95{-}4.2~\text{Å}$. The dependence of
$\unicode[STIX]{x1D706}=3.95{-}4.2~\text{Å}$. The dependence of  $\unicode[STIX]{x1D702}_{\text{ph}}$ on
$\unicode[STIX]{x1D702}_{\text{ph}}$ on  $L_{z}$ is shown in Figure 4(b).
$L_{z}$ is shown in Figure 4(b).
As seen from Figure 4, the optimal position of the laser focusing point along the gas expansion axis was reached when the distance from the nozzle outlet was  $L_{z}=2~\text{mm}$. Focusing on this point allowed for creating the clean X-ray source with energy
$L_{z}=2~\text{mm}$. Focusing on this point allowed for creating the clean X-ray source with energy  $E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ and the amount of X-ray photons per laser shot about
$E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ and the amount of X-ray photons per laser shot about  $\unicode[STIX]{x1D702}_{\text{ph}}\sim 3\times 10^{10}~\text{photons}/\text{shot}$. Figure 4(c) demonstrates the results of hydrodynamic calculations of the gas jet density profile for a rather similar slit nozzle considered in Refs. [Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Koester, Bussolino, Cristoforetti, Faenov, Giulietti, Giulietti, Labate, Levato, Pikuz and Gizzi35]. The gas density profile at the distance from the nozzle outlet
$\unicode[STIX]{x1D702}_{\text{ph}}\sim 3\times 10^{10}~\text{photons}/\text{shot}$. Figure 4(c) demonstrates the results of hydrodynamic calculations of the gas jet density profile for a rather similar slit nozzle considered in Refs. [Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Koester, Bussolino, Cristoforetti, Faenov, Giulietti, Giulietti, Labate, Levato, Pikuz and Gizzi35]. The gas density profile at the distance from the nozzle outlet  $L_{z}=2{-}4~\text{mm}$ has a form that visually looks like the X-ray emission dependence shown in Figure 4(b). Note that, the molecular densities for distances
$L_{z}=2{-}4~\text{mm}$ has a form that visually looks like the X-ray emission dependence shown in Figure 4(b). Note that, the molecular densities for distances  $L_{z}=1~\text{mm}$ and
$L_{z}=1~\text{mm}$ and  $L_{z}=2~\text{mm}$ are quite close as shown in Figure 4(c) and discussed in Refs. [Reference Zhang, Chen, Wang, Yan, Yuan, Mao, Wang, Liu, Shen, Faenov, Pikuz, Li, Li, Dong, Lu, Ma, Wei, Sheng and Zhang17, Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Koester, Bussolino, Cristoforetti, Faenov, Giulietti, Giulietti, Labate, Levato, Pikuz and Gizzi35]. Note that, the position
$L_{z}=2~\text{mm}$ are quite close as shown in Figure 4(c) and discussed in Refs. [Reference Zhang, Chen, Wang, Yan, Yuan, Mao, Wang, Liu, Shen, Faenov, Pikuz, Li, Li, Dong, Lu, Ma, Wei, Sheng and Zhang17, Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Koester, Bussolino, Cristoforetti, Faenov, Giulietti, Giulietti, Labate, Levato, Pikuz and Gizzi35]. Note that, the position  $L_{z}\leqslant 1~\text{mm}$ is usually chosen as the most effective for purposes of the wakefield electron acceleration in a laser–gas jet interaction[Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Koester, Bussolino, Cristoforetti, Faenov, Giulietti, Giulietti, Labate, Levato, Pikuz and Gizzi35]. It is associated not only with a cluster formation regime, but mostly explained by high sensitivity of a laser self-focusing process to a gas area shape. We stressed that the detailed consideration of electron acceleration regimes implies comprehensive particle-in-cell simulations and remains out of the scope of the paper.
$L_{z}\leqslant 1~\text{mm}$ is usually chosen as the most effective for purposes of the wakefield electron acceleration in a laser–gas jet interaction[Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Koester, Bussolino, Cristoforetti, Faenov, Giulietti, Giulietti, Labate, Levato, Pikuz and Gizzi35]. It is associated not only with a cluster formation regime, but mostly explained by high sensitivity of a laser self-focusing process to a gas area shape. We stressed that the detailed consideration of electron acceleration regimes implies comprehensive particle-in-cell simulations and remains out of the scope of the paper.
On the one hand, the effective electron acceleration can provide X-ray emission increase in the energy range  ${\sim}100{-}300~\text{eV}$ because of electrons deceleration on gas area atoms. On the other hand, such a source could not be considered as a clean X-ray source. Figure 4(b) also confirmed decreasing of keV X-ray emission at
${\sim}100{-}300~\text{eV}$ because of electrons deceleration on gas area atoms. On the other hand, such a source could not be considered as a clean X-ray source. Figure 4(b) also confirmed decreasing of keV X-ray emission at  $L_{z}\leqslant 2~\text{mm}$. Thus, the focusing point distances from the nozzle outlet as
$L_{z}\leqslant 2~\text{mm}$. Thus, the focusing point distances from the nozzle outlet as  $L_{z}\geqslant 2~\text{mm}$ satisfy the conditions of the clean X-ray source formation. However, the
$L_{z}\geqslant 2~\text{mm}$ satisfy the conditions of the clean X-ray source formation. However, the  $L_{z}$ increase is limited since it leads to fast decreasing of the X-ray emission intensity. So,
$L_{z}$ increase is limited since it leads to fast decreasing of the X-ray emission intensity. So,  $L_{z}=2~\text{mm}$ was an optimum distance for clean and effective keV X-ray source formation in the femtosecond relativistic laser plasma.
$L_{z}=2~\text{mm}$ was an optimum distance for clean and effective keV X-ray source formation in the femtosecond relativistic laser plasma.

Figure 6. (a) The comparison of the Ar plasma X-ray emission spectra measured for two different laser pulse energies  $E_{\text{las}}=50$ and
$E_{\text{las}}=50$ and  $E_{\text{las}}=280~\text{mJ}$ and kinetic modeling carried out with the PrismSpect. The calculations have been done for the fixed parameters: the ion density of the Ar gas jet –
$E_{\text{las}}=280~\text{mJ}$ and kinetic modeling carried out with the PrismSpect. The calculations have been done for the fixed parameters: the ion density of the Ar gas jet –  $N_{\text{i}}=5.2\times 10^{19}~\text{cm}^{-3}$, fraction 0.1% of hot electrons with
$N_{\text{i}}=5.2\times 10^{19}~\text{cm}^{-3}$, fraction 0.1% of hot electrons with  $T_{\text{hot}}=3~\text{keV}$. (b) Yield of X-ray photons with the energies
$T_{\text{hot}}=3~\text{keV}$. (b) Yield of X-ray photons with the energies  $E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ versus the incident laser pulse energy.
$E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ versus the incident laser pulse energy.

Figure 7. (a) X-ray emission spectra of Ar plasma; (b) X-ray photons yield –  $\unicode[STIX]{x1D702}_{\text{ph}}$ at the energy range
$\unicode[STIX]{x1D702}_{\text{ph}}$ at the energy range  $E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ versus the laser pulse duration –
$E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ versus the laser pulse duration –  $\unicode[STIX]{x1D70F}_{\text{las}}~(\text{fs})$; (c) X-ray photons yield –
$\unicode[STIX]{x1D70F}_{\text{las}}~(\text{fs})$; (c) X-ray photons yield –  $\unicode[STIX]{x1D702}_{\text{ph}}$ in the energy range
$\unicode[STIX]{x1D702}_{\text{ph}}$ in the energy range  $E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ versus entry Ar gas pressure –
$E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ versus entry Ar gas pressure –  $P_{\text{gas}}=3.5{-}9~\text{MPa}$, observed for the laser focusing position
$P_{\text{gas}}=3.5{-}9~\text{MPa}$, observed for the laser focusing position  $L_{z}=2~\text{mm}$ for diagnostic directions
$L_{z}=2~\text{mm}$ for diagnostic directions  $0^{\circ }$,
$0^{\circ }$,  $45^{\circ }$ and
$45^{\circ }$ and  $90^{\circ }$ toward the axis of the laser propagation direction.
$90^{\circ }$ toward the axis of the laser propagation direction.
The following parameter we considered is the laser pulse energy, since its variation directly affects the plasma heating and the properties of the X-ray emission consequently. X-ray emission spectra of argon plasma measured in three main diagnostic directions for different values of the laser pulse energy are shown in Figure 5.
As it is seen from Figure 5, varying the laser energy in the energy range  $E_{\text{las}}=50{-}280~\text{mJ}$ resulted in rather slight changes of the spectrum shape in comparison with variation of laser focusing point position, but significantly influences X-ray spectral intensities. In the case of the highest available facility laser energy on a target
$E_{\text{las}}=50{-}280~\text{mJ}$ resulted in rather slight changes of the spectrum shape in comparison with variation of laser focusing point position, but significantly influences X-ray spectral intensities. In the case of the highest available facility laser energy on a target  $(E_{\text{las}}=280~\text{mJ})$ measured spectra contain lines corresponding to transitions in He-, Li, -Be-like Ar ions and a peak intensity (
$(E_{\text{las}}=280~\text{mJ})$ measured spectra contain lines corresponding to transitions in He-, Li, -Be-like Ar ions and a peak intensity ( $1.5\times 10^{12}~\text{photons}/\text{Å}$ per shot) of the spectra is reached for the
$1.5\times 10^{12}~\text{photons}/\text{Å}$ per shot) of the spectra is reached for the  $\text{He}_{\unicode[STIX]{x1D6FC}1}$ line. Gradual decreasing of the laser energy led to appearance and relative intensity growth of the spectral lines associated with transitions in B-, C-, N-like argon ions. However, even at the energy
$\text{He}_{\unicode[STIX]{x1D6FC}1}$ line. Gradual decreasing of the laser energy led to appearance and relative intensity growth of the spectral lines associated with transitions in B-, C-, N-like argon ions. However, even at the energy  $E_{\text{las}}=50~\text{mJ}$ the relative intensity of the satellites did not exceed the intensity of resonant line
$E_{\text{las}}=50~\text{mJ}$ the relative intensity of the satellites did not exceed the intensity of resonant line  $\text{He}_{\unicode[STIX]{x1D6FC}1}$.
$\text{He}_{\unicode[STIX]{x1D6FC}1}$.
The comparison of X-ray spectra measured for the maximum laser energy on a target – 280 mJ and minimum – 50 mJ together with corresponding atomic calculations is shown in Figure 6(a).
We stressed that such X-ray intensity growth was identical for all the diagnostic directions. For the maximum laser energy at these experimental conditions –  $E_{\text{las}}=280~\text{mJ}$ the yield of X-ray photons with energies
$E_{\text{las}}=280~\text{mJ}$ the yield of X-ray photons with energies  $E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ reached
$E_{\text{x}\text{-}\text{ray}}\sim 3.1\;(\pm 0.2)~\text{keV}$ reached  $\unicode[STIX]{x1D702}_{\text{ph}}\sim 3.8\times 10^{10}~\text{photons}/\text{shot}$. We also observed the growth of X-ray emission due to increase of a laser pulse duration (see Figure 7).
$\unicode[STIX]{x1D702}_{\text{ph}}\sim 3.8\times 10^{10}~\text{photons}/\text{shot}$. We also observed the growth of X-ray emission due to increase of a laser pulse duration (see Figure 7).
Figure 7 brightly demonstrates the laser pulse duration increase from 40 fs to 100 fs led to the intense growth of the relative intensity of spectral lines corresponding to transitions in He-like and Li-like Ar ions. It resulted in  $40\%\pm 10\%$ X-ray emission intensity increase (see Figure 7(b)) up to
$40\%\pm 10\%$ X-ray emission intensity increase (see Figure 7(b)) up to  $\unicode[STIX]{x1D702}_{\text{ph}}\sim 7\;(\pm 0.5)\times 10^{10}~\text{photons}/\text{shot}$.
$\unicode[STIX]{x1D702}_{\text{ph}}\sim 7\;(\pm 0.5)\times 10^{10}~\text{photons}/\text{shot}$.
Note that, all the measured X-ray spectra do not contain the Ar  $\text{K}_{\unicode[STIX]{x1D6FC}}$ line, that appears when laser–solid interaction takes place. Absence of the Ar
$\text{K}_{\unicode[STIX]{x1D6FC}}$ line, that appears when laser–solid interaction takes place. Absence of the Ar  $\text{K}_{\unicode[STIX]{x1D6FC}}$ line in observed X-ray spectra is experimental confirmation of the direct laser–Ar gas jet interaction, not a laser–Ar cluster interaction as observed in Refs. [Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Nakai, Tsuji, Yamakawa, Hironaka, Kishimura, Morishita, Kondo and Nakamura37] and [Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Kishimoto, Yamakawa, Faenov, Magunov, Pikuz, Skobelev, Abdallah, Csanak, Boldarev and Gasilov12].
$\text{K}_{\unicode[STIX]{x1D6FC}}$ line in observed X-ray spectra is experimental confirmation of the direct laser–Ar gas jet interaction, not a laser–Ar cluster interaction as observed in Refs. [Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Nakai, Tsuji, Yamakawa, Hironaka, Kishimura, Morishita, Kondo and Nakamura37] and [Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Kishimoto, Yamakawa, Faenov, Magunov, Pikuz, Skobelev, Abdallah, Csanak, Boldarev and Gasilov12].
One more important parameter that can influence the X-ray emission intensity is inlet gas pressure –  $P_{\text{gas}}$. The dependence of X-ray photon yield on inlet gas pressure magnitude is shown in Figure 7(c). Contrary to the case of cluster target application, where the inlet gas pressure is of crucial importance[Reference Chen, Yan, Li, Hu, Zhang, Wang, Hafz, Mao, Huang, Ma, Zhao, Ma, Li, Lu, Sheng, Wei, Gao and Zhang2, Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Zhang, Chen, Yuan, Yan, Wang, Liu, Shen, Faenov, Pikuz, Skobelev, Gasilov, Boldarev, Mao, Li, Dong, Lu, Ma, Wang, Sheng and Zhang34, Reference Koester, Bussolino, Cristoforetti, Faenov, Giulietti, Giulietti, Labate, Levato, Pikuz and Gizzi35], the Ar gas jet X-ray emission weakly depends on the nozzle inlet pressure –
$P_{\text{gas}}$. The dependence of X-ray photon yield on inlet gas pressure magnitude is shown in Figure 7(c). Contrary to the case of cluster target application, where the inlet gas pressure is of crucial importance[Reference Chen, Yan, Li, Hu, Zhang, Wang, Hafz, Mao, Huang, Ma, Zhao, Ma, Li, Lu, Sheng, Wei, Gao and Zhang2, Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi25, Reference Zhang, Chen, Yuan, Yan, Wang, Liu, Shen, Faenov, Pikuz, Skobelev, Gasilov, Boldarev, Mao, Li, Dong, Lu, Ma, Wang, Sheng and Zhang34, Reference Koester, Bussolino, Cristoforetti, Faenov, Giulietti, Giulietti, Labate, Levato, Pikuz and Gizzi35], the Ar gas jet X-ray emission weakly depends on the nozzle inlet pressure –  $P_{\text{gas}}$ (see Figure 7(c)). The X-ray photon yield observed for all the diagnostic directions remained almost constant for a wide range of pressure from 2 to 9 MPa. Just for the gas pressure
$P_{\text{gas}}$ (see Figure 7(c)). The X-ray photon yield observed for all the diagnostic directions remained almost constant for a wide range of pressure from 2 to 9 MPa. Just for the gas pressure  $P_{\text{gas}}\sim 6~(\pm 0.25)~\text{MPa}$, we observed more intense X-ray emission, with an intensity increase of
$P_{\text{gas}}\sim 6~(\pm 0.25)~\text{MPa}$, we observed more intense X-ray emission, with an intensity increase of  $40\%\pm 10\%$.
$40\%\pm 10\%$.
4 Conclusion
We optimized the experimental conditions to generate a clean source of soft X-ray radiation with photon energies ( $E_{\text{x}\text{-}\text{ray}}$) of
$E_{\text{x}\text{-}\text{ray}}$) of  ${\sim}3.1\;(\pm 0.2)~\text{keV}$ in Ar gas jet relativistic plasma. This X-ray source can be successfully created by the interaction of high-contrast femtosecond laser pulses of relativistic intensity with Ar supersonic jets when this interaction leads to the formation of plasma with the typical electron temperature
${\sim}3.1\;(\pm 0.2)~\text{keV}$ in Ar gas jet relativistic plasma. This X-ray source can be successfully created by the interaction of high-contrast femtosecond laser pulses of relativistic intensity with Ar supersonic jets when this interaction leads to the formation of plasma with the typical electron temperature  $T_{\text{e}}\sim 185~\text{eV}$, electron density
$T_{\text{e}}\sim 185~\text{eV}$, electron density  $N_{\text{e}}\sim 7\times 10^{20}~\text{cm}^{-3}$ and mean charge
$N_{\text{e}}\sim 7\times 10^{20}~\text{cm}^{-3}$ and mean charge  $Z\sim 14$. We found that such plasma parameters can be attained for the following experimental conditions: the laser energy flux density on the target
$Z\sim 14$. We found that such plasma parameters can be attained for the following experimental conditions: the laser energy flux density on the target  $I_{\text{las}}\sim 1\times 10^{19}~\text{W}/\text{cm}^{2}$, the laser pulse energy
$I_{\text{las}}\sim 1\times 10^{19}~\text{W}/\text{cm}^{2}$, the laser pulse energy  $E_{\text{las}}=280~\text{mJ}$, the duration of laser pulse
$E_{\text{las}}=280~\text{mJ}$, the duration of laser pulse  $\unicode[STIX]{x1D70F}_{\text{las}}\sim 100~\text{fs}$ and the inlet gas pressure of
$\unicode[STIX]{x1D70F}_{\text{las}}\sim 100~\text{fs}$ and the inlet gas pressure of  $P_{\text{gas}}\sim 6~\text{MPa}$. We demonstrated that the focusing point position is the most important parameter for the purpose of optimization. For the clean and effective X-ray source creation, a laser beam must be focused 2 mm far from the slit nozzle[Reference Hosokai, Kinoshita, Watanabe, Yoshii, Ueda, Zhidokov, Uesaka, Nakajima, Kando, Kotaki and Kansai24] outlet on the jet central axis. Such focusing geometry makes it possible to efficiently convert laser energy to
$P_{\text{gas}}\sim 6~\text{MPa}$. We demonstrated that the focusing point position is the most important parameter for the purpose of optimization. For the clean and effective X-ray source creation, a laser beam must be focused 2 mm far from the slit nozzle[Reference Hosokai, Kinoshita, Watanabe, Yoshii, Ueda, Zhidokov, Uesaka, Nakajima, Kando, Kotaki and Kansai24] outlet on the jet central axis. Such focusing geometry makes it possible to efficiently convert laser energy to  $3.1\;(\pm 0.2)~\text{keV}$ X-ray radiation with flux
$3.1\;(\pm 0.2)~\text{keV}$ X-ray radiation with flux  $\unicode[STIX]{x1D702}_{\text{ph}}\sim 7\times 10^{10}~\text{photons}/\text{shot}$ or
$\unicode[STIX]{x1D702}_{\text{ph}}\sim 7\times 10^{10}~\text{photons}/\text{shot}$ or  $2.5\times 10^{11}~\text{photon}/\text{J}$ and conversion efficiency
$2.5\times 10^{11}~\text{photon}/\text{J}$ and conversion efficiency  $8.57\times 10^{-5}$. The experimental results confirmed the isotropy of the X-ray source radiation toward the observation directions (see Figures 6 and 7(c)) and a linear increase in the X-ray yield from
$8.57\times 10^{-5}$. The experimental results confirmed the isotropy of the X-ray source radiation toward the observation directions (see Figures 6 and 7(c)) and a linear increase in the X-ray yield from  $5\times 10^{9}$ to
$5\times 10^{9}$ to  $4\times 10^{10}~\text{photons}/\text{shot}$ with growth of the laser pulse energy from 50 to 280 mJ. We also demonstrated as in the case of Ar cluster plasma[Reference Magunov, Pikuz, Skobelev, Faenov, Blasco, Dorchies, Caillaud, Bonte, Salin, Stenz, Loboda, Litvinenko, Popova, Baidin, Junkel-Vives and Abdallah38, Reference Fukuda, Faenov, Tampo, Pikuz, Nakamura, Kando, Hayashi, Yogo, Sakaki, Kameshima, Pirozhkov, Ogura, Mori, Esirkepov, Koga, Boldarev, Gasilov, Magunov, Yamauchi, Kodama, Bolton, Kato, Tajima, Daido and Bulanov39] that the increase in the laser pulse duration from 40 fs to 100 fs results in
$4\times 10^{10}~\text{photons}/\text{shot}$ with growth of the laser pulse energy from 50 to 280 mJ. We also demonstrated as in the case of Ar cluster plasma[Reference Magunov, Pikuz, Skobelev, Faenov, Blasco, Dorchies, Caillaud, Bonte, Salin, Stenz, Loboda, Litvinenko, Popova, Baidin, Junkel-Vives and Abdallah38, Reference Fukuda, Faenov, Tampo, Pikuz, Nakamura, Kando, Hayashi, Yogo, Sakaki, Kameshima, Pirozhkov, Ogura, Mori, Esirkepov, Koga, Boldarev, Gasilov, Magunov, Yamauchi, Kodama, Bolton, Kato, Tajima, Daido and Bulanov39] that the increase in the laser pulse duration from 40 fs to 100 fs results in  $40\%\pm 10\%$ growth of the X-ray photon yield (see Figures 7(a) and 7(b)). Varying the inlet gas pressure results in a change in the X-ray photon yield by a factor of 2–3. However, we found experimentally that the optimum inlet pressure of Ar corresponding to the maximum of the X-ray emission exists and is reached for
$40\%\pm 10\%$ growth of the X-ray photon yield (see Figures 7(a) and 7(b)). Varying the inlet gas pressure results in a change in the X-ray photon yield by a factor of 2–3. However, we found experimentally that the optimum inlet pressure of Ar corresponding to the maximum of the X-ray emission exists and is reached for  $P_{\text{gas}}=6\;(\pm 0.25)~\text{MPa}$. Decreasing of the X-ray yield at lower Ar gas pressure
$P_{\text{gas}}=6\;(\pm 0.25)~\text{MPa}$. Decreasing of the X-ray yield at lower Ar gas pressure  $P_{\text{gas}}<6~\text{MPa}$ corresponds to deficient amount of Ar atoms to be ionized during the laser-target interaction time. Following decreasing of the X-ray yield at
$P_{\text{gas}}<6~\text{MPa}$ corresponds to deficient amount of Ar atoms to be ionized during the laser-target interaction time. Following decreasing of the X-ray yield at  $P_{\text{gas}}\geqslant 6~\text{MPa}$ probably happens due to X-ray absorption in a gas surrounding the small-size interaction region.
$P_{\text{gas}}\geqslant 6~\text{MPa}$ probably happens due to X-ray absorption in a gas surrounding the small-size interaction region.
The results we obtained confirm that the plasma generated as a result of interaction of high-contrast relativistic femtosecond laser pulses with argon supersonic gas jets can be considered a clean, compact, pulsed source of soft X-ray radiation. It is a unique object for fundamental investigation and also the effective X-ray source for a wide range of practical applications, including adsorption radiography and obtaining phase-contrast images.
Acknowledgement
The reported study was funded by RFBR according to the research project No. 18-52-53033 and National Natural Science Foundation of China (No. 11811530076).