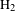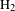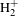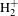1 Introduction
Both electronic and nuclear vibrational dynamics play a crucial role in molecular reactions, such as molecular ionization, dissociation and isomerization[Reference Yamanouchi1]. In general, nuclear vibrational dynamics happens on time scales from tens of femtoseconds up to hundreds of femtoseconds, while the valence electronic dynamics take place on the sub-femtosecond/attosecond time scale[Reference Ranitovic, Hogle, Rivière, Palacios, Tong, Toshima, González-Castrillo, Martin, Martin, Murnane and Kapteyn2]. Therefore, techniques with attosecond temporal resolution are required to gain insight into the dynamics of valence electrons in molecules. Experimental techniques such as attosecond extreme-ultraviolet or x-ray transient absorption spectroscopy[Reference Goulielmakis, Loh, Wirth, Santra, Rohringer, Yakovlev, Zherebtsov, Pfeifer, Azzeer, Kling, Leone and Krausz3–Reference Loh and Leone6], high harmonic spectroscopy[Reference Smirnova, Mairesse, Patchkovskii, Dudovich, Villeneuve, Corkum and Ivanov7–Reference Wörner, Bertrand, Fabre, Higuet, Ruf, Dubrouil, Patchkovskii, Spanner, Mairesse, Blanchet, Mével, Constant, Corkum and Villeneuve9] and photoelectron spectroscopy based on electron wave packet (EWP) interferences[Reference Gopal, Simeonidis, Moshammer, Ergler, Dürr, Kurka, Kühnel, Tschuch, Schröter, Bauer, Ullrich, Rudenko, Herrwerth, Uphues, Schultze, Goulielmakis, Uiberacker, Lezius and Kling10–Reference Xie15], have been demonstrated in studies of attosecond electronic dynamics in atoms and molecules[Reference Krausz and Ivanov16]. To retrieve the motion of valence electrons in a molecule, not only attosecond temporal resolution is required but also information on the involved molecular orbitals and the geometry of the molecule is critical. Since the EWPs released during tunneling ionization of molecules carry phase information on the molecular orbital where they are emitted from[Reference Xie, Jordan, Wickenhauser and Scrinzi17], this information can be retrieved from the interference patterns of EWPs in photoelectron spectra. Over the last few years, EWP interferometry has been applied in studies of ionization dynamics[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12], imaging molecular orbitals[Reference Meckel, Comtois, Zeidler, Staudte, Pavicic, Bandulet, Pepin, Kieffer, Dörner, Villeneuve and Corkum18] and the influence of the ionic Coulomb potential[Reference Huismans, Rouzée, Gijsbertsen, Jungmann, Smolkowska, Logman, Lépine, Cauchy, Zamith, Marchenko, Bakker, Berden, Redlich, van der Meer, Muller, Vermin, Schafer, Spanner, Ivanov, Smirnova, Bauer, Popruzhenko and Vrakking11, Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19]. With the phase of the interfering EWPs can be reconstructed, dynamical information taking place during the strong field interaction can be read out from the interference pattern with attosecond temporal resolution[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12].
Four types of strong-field-induced EWP interferences in molecules can be distinguished: the first type is the inter-cycle interference (ICI) produced by EWPs released during different optical cycles which lead to above-threshold ionization (ATI)-like structures in the momentum or the energy distribution of photoelectrons[Reference Boguslavskiy, Mikosch, Gijsbertsen, Spanner, Patchkovskii, Gador, Vrakking and Stolow13, Reference Arbó, Ishikawa, Schiessl, Persson and Burgdörfer20]. The second type is the so-called subcycle interference (SCI) formed by EWPs detached during different half cycles within one optical cycle[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12, Reference Lindner, Schätzel, Walther, Baltuška, Goulielmakis, Krausz, Milošević, Bauer, Becker and Paulus21–Reference Arbó, Nagele, Tong, Xie, Kitzler and Burgdörfer23]. The third type of interference is formed by EWPs removed from the system during the same quarter of one optical cycle due to scattering on the ionic potential[Reference Huismans, Rouzée, Gijsbertsen, Jungmann, Smolkowska, Logman, Lépine, Cauchy, Zamith, Marchenko, Bakker, Berden, Redlich, van der Meer, Muller, Vermin, Schafer, Spanner, Ivanov, Smirnova, Bauer, Popruzhenko and Vrakking11, Reference Spanner, Smirnova, Corkum and Ivanov24, Reference Bian and Bandrauk25]. The fourth type is multi-center interference due to EWPs scattering on different nuclei of a molecule[Reference Spanner, Smirnova, Corkum and Ivanov24, Reference Yurchenko, Patchkovskii, Litvinyuk, Corkum and Yudin26]. Accurately defined momentum-to-time mapping and a precise identification of the type of observed interference fringes is necessary for retrieving the information on the electronic dynamics and structures from the measured interference pattern. Previous studies revealed that it is important to consider the influence of the ionic Coulomb potential on the interference patterns[Reference Huismans, Rouzée, Gijsbertsen, Jungmann, Smolkowska, Logman, Lépine, Cauchy, Zamith, Marchenko, Bakker, Berden, Redlich, van der Meer, Muller, Vermin, Schafer, Spanner, Ivanov, Smirnova, Bauer, Popruzhenko and Vrakking11, Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12, Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19, Reference Zhang, Xie, Roither, Kartashov, Wang, Wang, Schöffler, Shafir, Corkum, Baltuška, Ivanov, Kheifets, Liu, Staudte and Kitzler27]. However, this is not a trivial task. Besides, the existence of the mixture of different kinds of interferences and complicated low-energy structures (LES)[Reference Blaga, Catoire, Colosimo, Paulus, Muller, Agostini and Dimauro28–Reference Dimitrovski, Maurer, Stapelfeldt and Madsen31], affects the positions of the fringe positions will be modified which influences the precision of the phase reconstruction[Reference Arbó, Ishikawa, Schiessl, Persson and Burgdörfer20].
To obtain a well-defined interference pattern of EWPs, a cycle-shaped laser field is beneficial, because the EWP interference patterns are induced by EWPs released at different times. Their release times are thus extremely sensitive to the shape of the laser field and can be controlled by the shape of the cycle of the laser field. There are several ways to obtain such laser fields. One of the most straightforward methods is to stabilize the carrier-envelope phase of a few-cycle laser pulse. Another method is to lock the phase delay between multiple laser fields with different colors. Such cycle-shaped laser fields have been applied to controlling high harmonic generation[Reference Goulielmakis, Schultze, Hofstetter, Yakovlev, Gagnon, Uiberacker, Aquila, Gullikson, Attwood, Kienberger, Krausz and Kleineberg32, Reference Haessler, Balčiunas, Fan, Andriukaitis, Pugžlys, Baltuška, Witting, Squibb, Zaïr, Tisch, Marangos and Chipperfield33], molecular orientation[Reference De, Znakovskaya, Ray, Anis, Johnson, Bocharova, Magrakvelidze, Esry, Cocke, Litvinyuk and Kling34] and dissociation[Reference Ray, He, De, Cao, Mashiko, Ranitovic, Singh, Znakovskaya, Thumm, Paulus, Kling, Litvinyuk and Cocke35], and single and double ionization of atoms[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12, Reference Zhang, Xie, Roither, Kartashov, Wang, Wang, Schöffler, Shafir, Corkum, Baltuška, Ivanov, Kheifets, Liu, Staudte and Kitzler27, Reference Zhang, Xie, Roither, Zhou, Lu, Kartashov, Schöffler, Shafir, Corkum, Baltuška, Staudte and Kitzler36].
In this work, we employed a two-color laser field with precise control over the relative phase between a fundamental laser field and its second harmonic. In a previous study[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12], we have demonstrated that subcycle ionization dynamics can be retrieved from the SCI patterns of atomic targets created by such two-color laser fields. It has been shown that with a cycle-shaped two-color laser field the final momentum of electrons can be shifted to bigger momentum values to avoid overlapping with the complex LES and to minimize the influence from the Coulomb potential[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12].
In the case of molecules, because of the small differences in the ionization potentials and the different angular dependence of ionization rates for different orbitals, tunnel ionization may happen from lower lying molecular orbitals rather than only from the HOMO[Reference Wu, Schmidt, Kunitski, Meckel, Voss, Sann, Kim, Jahnke, Czasch and Dörner37]. Moreover, the strong field interaction may lead to dissociation of the molecule along different pathways[Reference Xie, Doblhoff-Dier, Roither, Schöffler, Kartashov, Xu, Rathje, Paulus, Baltuška, Gräfe and Kitzler38], typically leading to different combinations of photo-ions, which are often addressed as channels. To get access to the electron dynamics of molecular ionization, discrimination between these different channels is necessary. Here we extend subcycle EWP interferometry from atoms to molecules using coincidence measurements which allow disentangling the different contributions of the various possible channels to interference structures in measured photoelectron momentum distributions. For our proof-of-principle measurements we chose the simplest molecule, hydrogen (
![]() $\text{H}_{2}$
), as the target.
$\text{H}_{2}$
), as the target.
A schematic view of subcycle EWP interference is shown in Figure 1. The EWPs released at different times within one laser optical cycle may end at the same final momentum and therefore interfere with each other in the momentum space. Measurement of the photoelectron momentum distribution with a reaction microscope allows recording these interferences[Reference Dörner, Mergel, Jagutzki, Ullrich, Spielberger, Moshammer and Schmidt-Böcking39, Reference Ullrich, Moshammer, Dorn, Dörner, Schmidt and Schmidt-Böcking40].

Figure 1. A schematic view of subcycle EWP interferences. When a molecule is exposed to a two-color laser field, shown as the magenta line, EWPs will be released around the field’s peaks. In a unit cell of the pulse, the EWPs released during each half cycle (t1 and t2) will lead to the same final momentum p, which leads to interference fringes in the momentum space.
2 Experiments
Coincidence measurements of electrons and ions were performed for
![]() $\text{H}_{2}$
with a reaction microscope. A laser beam from a home-built Ti:sapphire laser amplifier system with a center wavelength of 795 nm, a repetition rate of 5 kHz and a pulse duration (full width at half maximum of the intensity) of about 25 fs is superimposed with the second harmonic beam generated with a
$\text{H}_{2}$
with a reaction microscope. A laser beam from a home-built Ti:sapphire laser amplifier system with a center wavelength of 795 nm, a repetition rate of 5 kHz and a pulse duration (full width at half maximum of the intensity) of about 25 fs is superimposed with the second harmonic beam generated with a
![]() $500~\unicode[STIX]{x03BC}\text{m}$
type-I BBO crystal. The pulse duration of the second harmonic pulse was 46 fs according to self diffraction frequency resolved optical gating (FROG) measurements. The second harmonic beam was polarized parallel to the fundamental beam and the peak laser intensities were about
$500~\unicode[STIX]{x03BC}\text{m}$
type-I BBO crystal. The pulse duration of the second harmonic pulse was 46 fs according to self diffraction frequency resolved optical gating (FROG) measurements. The second harmonic beam was polarized parallel to the fundamental beam and the peak laser intensities were about
![]() $6\times 10^{13}~\text{W}~\text{cm}^{-2}$
for each beam. The group velocity delay between the two laser pulses was compensated by calcite plates and a pair of fused silica wedges which was also used to adjust the phase delay between the two colors in steps of
$6\times 10^{13}~\text{W}~\text{cm}^{-2}$
for each beam. The group velocity delay between the two laser pulses was compensated by calcite plates and a pair of fused silica wedges which was also used to adjust the phase delay between the two colors in steps of
![]() $0.06\unicode[STIX]{x1D70B}$
. The calibration of the relative phase between the two colors and the laser peak intensities was done using reference measurements on helium, as described in Ref. [Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12]. A weak homogeneous dc field of
$0.06\unicode[STIX]{x1D70B}$
. The calibration of the relative phase between the two colors and the laser peak intensities was done using reference measurements on helium, as described in Ref. [Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12]. A weak homogeneous dc field of
![]() $2.5~\text{V}~\text{cm}^{-1}$
was applied along the time-of-flight (TOF) spectrometer to accelerate electrons and ions toward two position-sensitive multi-channel plate detectors. In addition, a homogeneous magnetic field of 6.4 gauss ensures
$2.5~\text{V}~\text{cm}^{-1}$
was applied along the time-of-flight (TOF) spectrometer to accelerate electrons and ions toward two position-sensitive multi-channel plate detectors. In addition, a homogeneous magnetic field of 6.4 gauss ensures
![]() $4\unicode[STIX]{x1D70B}$
detection of electrons. The beam of hydrogen molecules with a diameter of about
$4\unicode[STIX]{x1D70B}$
detection of electrons. The beam of hydrogen molecules with a diameter of about
![]() $170~\unicode[STIX]{x03BC}\text{m}$
is prepared by supersonic expansion of
$170~\unicode[STIX]{x03BC}\text{m}$
is prepared by supersonic expansion of
![]() $\text{H}_{2}$
gas through a nozzle with a diameter of
$\text{H}_{2}$
gas through a nozzle with a diameter of
![]() $30~\unicode[STIX]{x03BC}\text{m}$
and collimation with a two-stage skimmer before the ultra-high vacuum interaction chamber (background pressure about
$30~\unicode[STIX]{x03BC}\text{m}$
and collimation with a two-stage skimmer before the ultra-high vacuum interaction chamber (background pressure about
![]() $1.3\times 10^{-10}~\text{mbar}$
). TOFs and positions of electrons and ions are recorded and the momentum vectors of all particles are retrieved in the off-line data analysis. Momentum conservation conditions between electrons and ions can be applied to minimize the background signals. To ensure a high efficiency of coincidence detection, the ionization rate was kept at about 0.4 ionization events per laser shot. More details on the experimental setup can be found in our previous publications[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12, Reference Xie, Doblhoff-Dier, Roither, Schöffler, Kartashov, Xu, Rathje, Paulus, Baltuška, Gräfe and Kitzler38].
$1.3\times 10^{-10}~\text{mbar}$
). TOFs and positions of electrons and ions are recorded and the momentum vectors of all particles are retrieved in the off-line data analysis. Momentum conservation conditions between electrons and ions can be applied to minimize the background signals. To ensure a high efficiency of coincidence detection, the ionization rate was kept at about 0.4 ionization events per laser shot. More details on the experimental setup can be found in our previous publications[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12, Reference Xie, Doblhoff-Dier, Roither, Schöffler, Kartashov, Xu, Rathje, Paulus, Baltuška, Gräfe and Kitzler38].
3 Results and discussion
3.1
 $H_{2}$
in two-color laser fields
$H_{2}$
in two-color laser fields
When a hydrogen molecule interacts with a strong laser field, one electron can be removed through tunnel ionization. After single ionization, the molecule will reach a cationic state.
![]() $\text{H}_{2}^{+}$
may then dissociate into a proton and a hydrogen atom, or
$\text{H}_{2}^{+}$
may then dissociate into a proton and a hydrogen atom, or
![]() $\text{H}_{2}^{+}$
can be further ionized and eventually Coulomb-explored into two protons. A typical TOF spectrum of
$\text{H}_{2}^{+}$
can be further ionized and eventually Coulomb-explored into two protons. A typical TOF spectrum of
![]() $\text{H}_{2}$
in a strong two-color laser field is presented in Figure 2. The single ionization (
$\text{H}_{2}$
in a strong two-color laser field is presented in Figure 2. The single ionization (
![]() $\text{H}_{2}^{+}$
), dissociation (
$\text{H}_{2}^{+}$
), dissociation (
![]() $\text{H}^{+}+\text{H}$
) and Coulomb explosion (
$\text{H}^{+}+\text{H}$
) and Coulomb explosion (
![]() $\text{H}^{+}+\text{H}^{+}$
) channels can be well distinguished. As marked in Figure 2, there are two pathways for the dissociation of
$\text{H}^{+}+\text{H}^{+}$
) channels can be well distinguished. As marked in Figure 2, there are two pathways for the dissociation of
![]() $\text{H}_{2}^{+}$
: above-threshold dissociation (ATD) leading to protons with high energy, and zero-photon dissociation (ZPD) leading to low-energy protons[Reference Moser and Gibson41, Reference Posthumus, Plumridge, Frasinski, Codling, Divall, Langley and Taday42]. As the protons generated along these different pathways can be easily distinguished by their momenta, we can distinguish three different channels resulting from singly charged hydrogen, namely the non-fragmenting channel that results in
$\text{H}_{2}^{+}$
: above-threshold dissociation (ATD) leading to protons with high energy, and zero-photon dissociation (ZPD) leading to low-energy protons[Reference Moser and Gibson41, Reference Posthumus, Plumridge, Frasinski, Codling, Divall, Langley and Taday42]. As the protons generated along these different pathways can be easily distinguished by their momenta, we can distinguish three different channels resulting from singly charged hydrogen, namely the non-fragmenting channel that results in
![]() $\text{H}_{2}^{+}$
and the ATD and ZPD channels.
$\text{H}_{2}^{+}$
and the ATD and ZPD channels.

Figure 2. TOF spectrum of
![]() $\text{H}_{2}$
interacting with two-color laser fields. In the
$\text{H}_{2}$
interacting with two-color laser fields. In the
![]() $\text{H}^{+}$
distribution, there are three regions: ZPD, ATD and Coulomb explosion (CE).
$\text{H}^{+}$
distribution, there are three regions: ZPD, ATD and Coulomb explosion (CE).
First we focus on the channel leading to
![]() $\text{H}_{2}^{+}$
. A measured electron momentum distribution correlated with
$\text{H}_{2}^{+}$
. A measured electron momentum distribution correlated with
![]() $\text{H}_{2}^{+}$
is shown in Figure 3, integrated over all relative two-color phases. In the distribution there appear two clear types of structures: finger-like patterns due to scattering of EWPs on the parent nucleus and ATI-like ring structures. Here in this paper, we focus on SCI of EWPs released during strong field interaction. However, in the phase-integrated spectrum shown in Figure 3 there are no clear structures of subcycle EWP interferences visible. The reason is that the subcycle EWP interference is very sensitive to the cycle shape of the laser field. As the electron momentum distribution in Figure 3 is integrated over all relative phases between the two-color fields, the structures created by SCI are smeared out.
$\text{H}_{2}^{+}$
is shown in Figure 3, integrated over all relative two-color phases. In the distribution there appear two clear types of structures: finger-like patterns due to scattering of EWPs on the parent nucleus and ATI-like ring structures. Here in this paper, we focus on SCI of EWPs released during strong field interaction. However, in the phase-integrated spectrum shown in Figure 3 there are no clear structures of subcycle EWP interferences visible. The reason is that the subcycle EWP interference is very sensitive to the cycle shape of the laser field. As the electron momentum distribution in Figure 3 is integrated over all relative phases between the two-color fields, the structures created by SCI are smeared out.
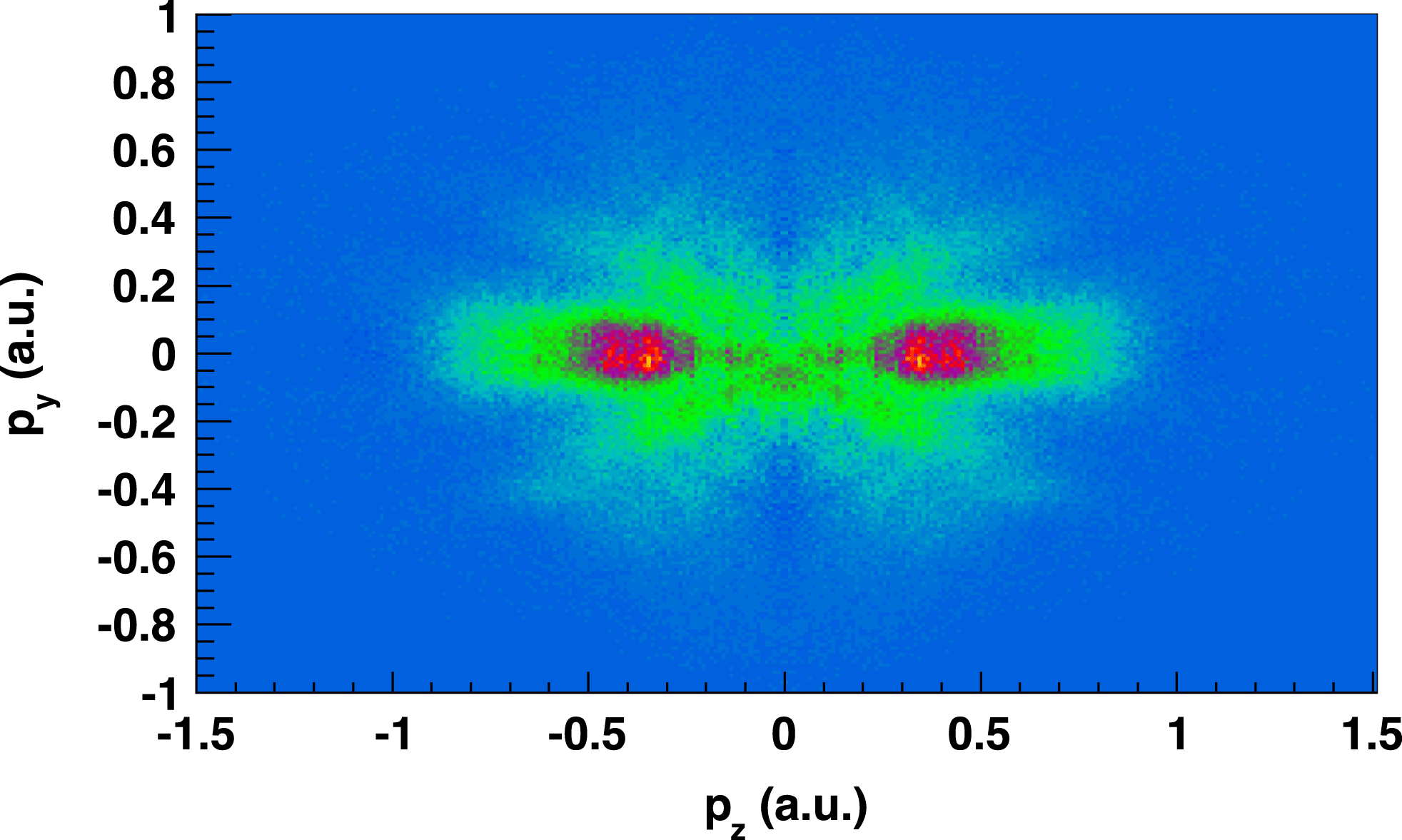
Figure 3. A slice through a measured electron momentum distribution in the
![]() $x{-}z$
plane (laser field polarization along
$x{-}z$
plane (laser field polarization along
![]() $z$
-direction) with a condition
$z$
-direction) with a condition
![]() $|p_{y}|<0.1$
a.u. and integration over all relative phases of the two-color laser fields. Momentum conservation conditions between one electron and
$|p_{y}|<0.1$
a.u. and integration over all relative phases of the two-color laser fields. Momentum conservation conditions between one electron and
![]() $\text{H}_{2}^{+}$
are applied to the measured data to ensure coincidence selection. To enhance the visibility of structures induced by EWP interferences, a gaussian function is subtracted from the momentum distribution for each relative phase[Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19].
$\text{H}_{2}^{+}$
are applied to the measured data to ensure coincidence selection. To enhance the visibility of structures induced by EWP interferences, a gaussian function is subtracted from the momentum distribution for each relative phase[Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19].
3.2 Photoelectron momentum distribution over relative phase
Measured distributions of the
![]() $\text{H}_{2}^{+}$
ionic momentum along the laser polarization direction (
$\text{H}_{2}^{+}$
ionic momentum along the laser polarization direction (
![]() $p_{z}$
) over the relative phase are shown in Figure 4(a). Clear
$p_{z}$
) over the relative phase are shown in Figure 4(a). Clear
![]() $2\unicode[STIX]{x1D70B}$
-periodic modulations can be seen. The mean momentum value oscillates over the relative phase [depicted in Figure 4(b) as red circles] and reaches maximum offset at
$2\unicode[STIX]{x1D70B}$
-periodic modulations can be seen. The mean momentum value oscillates over the relative phase [depicted in Figure 4(b) as red circles] and reaches maximum offset at
![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D719}=0.35+n\unicode[STIX]{x1D70B},n\in \mathbb{Z}$
. The mean value of the momentum distribution is determined by the shape of the laser field vector potential. For relative phase 0, the vector potential of the two-color field is symmetric which, according to predictions of the simple-man’s model within the strong field approximation (SFA)[Reference Corkum43], should lead to zero mean value. As shown previously, the observed offset from 0 is due to the influence of the ionic Coulomb potential[Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19, Reference Chelkowski, Bandrauk and Apolonski44, Reference Chelkowski and Bandrauk45]. The phase shift due the Coulomb potential is about
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D719}=0.35+n\unicode[STIX]{x1D70B},n\in \mathbb{Z}$
. The mean value of the momentum distribution is determined by the shape of the laser field vector potential. For relative phase 0, the vector potential of the two-color field is symmetric which, according to predictions of the simple-man’s model within the strong field approximation (SFA)[Reference Corkum43], should lead to zero mean value. As shown previously, the observed offset from 0 is due to the influence of the ionic Coulomb potential[Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19, Reference Chelkowski, Bandrauk and Apolonski44, Reference Chelkowski and Bandrauk45]. The phase shift due the Coulomb potential is about
![]() $-0.2\unicode[STIX]{x1D70B}$
as compared with the simple-man’s results, in which the Coulomb influence is neglected[Reference Chelkowski, Bandrauk and Apolonski44, Reference Chelkowski and Bandrauk45]. The momentum mean value of a measurement on helium with higher laser peak intensity (
$-0.2\unicode[STIX]{x1D70B}$
as compared with the simple-man’s results, in which the Coulomb influence is neglected[Reference Chelkowski, Bandrauk and Apolonski44, Reference Chelkowski and Bandrauk45]. The momentum mean value of a measurement on helium with higher laser peak intensity (
![]() $1\times 10^{13}~\text{W}~\text{cm}^{-2}$
for each color)[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12] is plotted for comparison in Figure 4(b) as blue squares. The amplitude of the mean value oscillation for helium is almost twice as that for hydrogen because of the higher peak laser intensity. On the other hand, we notice that the phase shift of the helium measurements is about
$1\times 10^{13}~\text{W}~\text{cm}^{-2}$
for each color)[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12] is plotted for comparison in Figure 4(b) as blue squares. The amplitude of the mean value oscillation for helium is almost twice as that for hydrogen because of the higher peak laser intensity. On the other hand, we notice that the phase shift of the helium measurements is about
![]() $-0.3\unicode[STIX]{x1D70B}$
, i.e., more than that of the hydrogen measurement. This contradicts our previous finding that the Coulomb effect is stronger for lower laser peak intensity[Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19]. The reason may be the participation of excited states or non-adiabatic effects in the ionization process of hydrogen[Reference Yudin and Ivanov46, Reference Spanner, Mikosch, Gijsbertsen, Boguslavskiy and Stolow47].
$-0.3\unicode[STIX]{x1D70B}$
, i.e., more than that of the hydrogen measurement. This contradicts our previous finding that the Coulomb effect is stronger for lower laser peak intensity[Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19]. The reason may be the participation of excited states or non-adiabatic effects in the ionization process of hydrogen[Reference Yudin and Ivanov46, Reference Spanner, Mikosch, Gijsbertsen, Boguslavskiy and Stolow47].

Figure 4. (a) Measured ion momentum distributions of
![]() $\text{H}_{2}^{+}$
along the laser polarization direction over the relative phase between the two colors. To enhance the visibility of structures induced by EWP interferences, a gaussian function is subtracted for each relative phase[Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19]. (b) The mean value of the momentum distributions of
$\text{H}_{2}^{+}$
along the laser polarization direction over the relative phase between the two colors. To enhance the visibility of structures induced by EWP interferences, a gaussian function is subtracted for each relative phase[Reference Xie, Roither, Gräfe, Kartashov, Persson, Lemell, Zhang, Schöffler, Baltuška, Burgdörfer and Kitzler19]. (b) The mean value of the momentum distributions of
![]() $\text{H}_{2}^{+}$
along the laser polarization direction as a function of the relative phase between the two colors. For comparison the same quantity for
$\text{H}_{2}^{+}$
along the laser polarization direction as a function of the relative phase between the two colors. For comparison the same quantity for
![]() $\text{He}^{+}$
is added to the figure. The gray line represents the simulated results using the SFA.
$\text{He}^{+}$
is added to the figure. The gray line represents the simulated results using the SFA.
3.3 Subcycle interferences of electron wave packets correlated with
 $H_{2}^{+}$
$H_{2}^{+}$
To observe SCI structures we investigate electron momentum distributions for certain relative phases between the two colors, since for electrons the momentum resolution is much higher than that for ions along the directions perpendicular to the laser polarization direction. The measured electron momentum distributions in the laser polarization plane are illustrated in Figures 5(f)–(j) for five different relative phases (0,
![]() $0.25\unicode[STIX]{x1D70B}$
,
$0.25\unicode[STIX]{x1D70B}$
,
![]() $0.5\unicode[STIX]{x1D70B}$
,
$0.5\unicode[STIX]{x1D70B}$
,
![]() $0.75\unicode[STIX]{x1D70B}$
and
$0.75\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}$
). The structures in the momentum distributions look similar to those measured for helium[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12]. There are narrow ATI-like peaks in the low momentum region as shown in the
$\unicode[STIX]{x1D70B}$
). The structures in the momentum distributions look similar to those measured for helium[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12]. There are narrow ATI-like peaks in the low momentum region as shown in the
![]() $p_{z}$
distributions that have been obtained by cutting a narrow cylinder along the laser polarization direction (
$p_{z}$
distributions that have been obtained by cutting a narrow cylinder along the laser polarization direction (
![]() $|p_{x,y}|<0.1$
a.u.) from the 3D momentum distributions [Figures 5(k)–(o)], and finger-like structures in the 2D momentum distributions [Figures 5(f)–(j)]. SCI structures can be seen in the 1D momentum distribution as broad peaks [Figures 5(k)–(o)]. As compared to the corresponding ones obtained earlier for helium[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12], the momentum distributions in Figures 5(k)–(o) for hydrogen differ in several details because of different laser intensities, different ionic potentials and energy structures.
$|p_{x,y}|<0.1$
a.u.) from the 3D momentum distributions [Figures 5(k)–(o)], and finger-like structures in the 2D momentum distributions [Figures 5(f)–(j)]. SCI structures can be seen in the 1D momentum distribution as broad peaks [Figures 5(k)–(o)]. As compared to the corresponding ones obtained earlier for helium[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12], the momentum distributions in Figures 5(k)–(o) for hydrogen differ in several details because of different laser intensities, different ionic potentials and energy structures.

Figure 5. (a)–(e) Electric fields (red lines) and vector potentials (blue lines) for relative two-color phases 0,
![]() $0.25\unicode[STIX]{x1D70B}$
,
$0.25\unicode[STIX]{x1D70B}$
,
![]() $0.5\unicode[STIX]{x1D70B}$
,
$0.5\unicode[STIX]{x1D70B}$
,
![]() $0.75\unicode[STIX]{x1D70B}$
and
$0.75\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}$
. (f)–(j) Measured electron momentum distributions in the laser polarization plane with subtraction of a gaussian function for the five relative phases. (k)–(o) Momentum distributions along the laser polarization direction with
$\unicode[STIX]{x1D70B}$
. (f)–(j) Measured electron momentum distributions in the laser polarization plane with subtraction of a gaussian function for the five relative phases. (k)–(o) Momentum distributions along the laser polarization direction with
![]() $|p_{x,y}|<0.1$
a.u. for the five relative phases. Vertical gray lines indicate the positions of the ATI peaks.
$|p_{x,y}|<0.1$
a.u. for the five relative phases. Vertical gray lines indicate the positions of the ATI peaks.
First, we focus on the results with relative phase 0. According to the shape of the vector potential [Figure 5(a)], the momentum distribution should be symmetric along the
![]() $p_{z}$
-coordinate. The measured momentum distribution in Figure 5(k) shows a pronounced asymmetry, though. This can be explained by the influence of the Coulomb potential of the ion, which influences the trajectories of the EWP such that an EWP released before the peak of the laser field will be driven back and will scatter with the parent ion which leads to the appearance of clear finger-like holographic structures. In the results for helium there are no obvious SCI structures visible[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12]. The reason is that for helium the ionization mainly happens near the major peak within one optical cycle and therefore the SCI structures are suppressed[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12]. In contrast, in the momentum distributions for
$p_{z}$
-coordinate. The measured momentum distribution in Figure 5(k) shows a pronounced asymmetry, though. This can be explained by the influence of the Coulomb potential of the ion, which influences the trajectories of the EWP such that an EWP released before the peak of the laser field will be driven back and will scatter with the parent ion which leads to the appearance of clear finger-like holographic structures. In the results for helium there are no obvious SCI structures visible[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12]. The reason is that for helium the ionization mainly happens near the major peak within one optical cycle and therefore the SCI structures are suppressed[Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12]. In contrast, in the momentum distributions for
![]() $\text{H}_{2}^{+}$
there appear SCI fringes for
$\text{H}_{2}^{+}$
there appear SCI fringes for
![]() $p_{z}>0.2$
a.u. [Figure 5(f,k)]. Within the SFA such structures are explained by the interference of EWPs released at
$p_{z}>0.2$
a.u. [Figure 5(f,k)]. Within the SFA such structures are explained by the interference of EWPs released at
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
, respectively, as indicated in Figure 5(a). The momenta after the laser pulse of EWPs released at
$t_{2}$
, respectively, as indicated in Figure 5(a). The momenta after the laser pulse of EWPs released at
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
will be equal which leads to SCI structures. The reason for the more pronounced SCI structure for a relative phase of 0 in hydrogen than in helium may be the following: the ionization potential of helium, 24.6 eV, is higher than that of hydrogen, 15.5 eV. Therefore, the ionization of helium dominantly happens near the main peak within a laser optical cycle, while in the ionization of hydrogen the two minor peaks also contribute considerably.
$t_{2}$
will be equal which leads to SCI structures. The reason for the more pronounced SCI structure for a relative phase of 0 in hydrogen than in helium may be the following: the ionization potential of helium, 24.6 eV, is higher than that of hydrogen, 15.5 eV. Therefore, the ionization of helium dominantly happens near the main peak within a laser optical cycle, while in the ionization of hydrogen the two minor peaks also contribute considerably.
For a relative phase of
![]() $0.5\unicode[STIX]{x1D70B}$
, the laser electric field is symmetric [Figure 5(c)]. Therefore, within one optical cycle, ionization happens equally at the two main peaks (
$0.5\unicode[STIX]{x1D70B}$
, the laser electric field is symmetric [Figure 5(c)]. Therefore, within one optical cycle, ionization happens equally at the two main peaks (
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
). The released EWPs will interfere with each other in the momentum space because they will end at the same final momentum. In Ref. [Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12] the SCI structures observed for a relative phase of
$t_{2}$
). The released EWPs will interfere with each other in the momentum space because they will end at the same final momentum. In Ref. [Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12] the SCI structures observed for a relative phase of
![]() $0.5\unicode[STIX]{x1D70B}$
are exploited for the retrieval of the relative phase of the released EWPs and to investigate the electron dynamics during strong field ionization. As shown in Figure 5(h), there exist clear SCI structures visible on the negative momentum side. A detailed analysis of these structures along the procedures described in Ref. [Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12] necessitates, however, intricate numerical modeling. As for
$0.5\unicode[STIX]{x1D70B}$
are exploited for the retrieval of the relative phase of the released EWPs and to investigate the electron dynamics during strong field ionization. As shown in Figure 5(h), there exist clear SCI structures visible on the negative momentum side. A detailed analysis of these structures along the procedures described in Ref. [Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler12] necessitates, however, intricate numerical modeling. As for
![]() $\text{H}_{2}$
this is a much more complex task than for He this is well beyond the scope of the current work.
$\text{H}_{2}$
this is a much more complex task than for He this is well beyond the scope of the current work.
When the relative phase between the two colors varies, the shape of the laser field’s cycle varies. Since tunneling ionization is very sensitive to the field strength of a laser field, the ionization time within an optical cycle depends delicately on the shape of the laser cycle. As a result, SCI structures can be sensitively controlled by varying the relative phase of the two-color field. As shown in Figure 5, the interference structures, especially the SCI structures, indeed strongly depend on the relative phase of the two colors.
3.4 Subcycle interferences of electron wave packets for dissociation channels
After single ionization in a two-color field,
![]() $\text{H}_{2}^{+}$
may dissociate into a proton and a hydrogen atom through ATD or ZPD. We can distinguish the dissociation channels based on the kinetic energy released during the dissociation process. By coincidence gating we can obtain the corresponding photoelectron spectra. From the such obtained photoelectron spectra we can get access to the electron and nuclear dynamics leading to the different dissociation channels. For
$\text{H}_{2}^{+}$
may dissociate into a proton and a hydrogen atom through ATD or ZPD. We can distinguish the dissociation channels based on the kinetic energy released during the dissociation process. By coincidence gating we can obtain the corresponding photoelectron spectra. From the such obtained photoelectron spectra we can get access to the electron and nuclear dynamics leading to the different dissociation channels. For
![]() $\text{H}_{2}$
these different channels can be easily separated by the proton momentum. We select the proton momentum in the range of
$\text{H}_{2}$
these different channels can be easily separated by the proton momentum. We select the proton momentum in the range of
![]() $6<|p_{z}|<11$
a.u. for ATD, and
$6<|p_{z}|<11$
a.u. for ATD, and
![]() $|p_{z}|<6$
a.u. for ZDP. Due to the relatively low dissociation probability of the ZPD channel, cf. the small proton yield in Figure 2 in the TOF range corresponding to ZPD, we could not obtain electron momentum distributions with high enough statistics to identify interference structures.
$|p_{z}|<6$
a.u. for ZDP. Due to the relatively low dissociation probability of the ZPD channel, cf. the small proton yield in Figure 2 in the TOF range corresponding to ZPD, we could not obtain electron momentum distributions with high enough statistics to identify interference structures.

Figure 6. Electron momentum distribution correlated with the ATD pathway for a relative two-color phase of 0.
In Figure 6 electron momentum distributions along the laser polarization direction are plotted for the ATD channel and a relative phase of 0. The structure is similar to that of the
![]() $\text{H}_{2}^{+}$
channel [Figure 5(f)]. This experimental observation of SCI in the strong field ionization of
$\text{H}_{2}^{+}$
channel [Figure 5(f)]. This experimental observation of SCI in the strong field ionization of
![]() $\text{H}_{2}$
, however, constitutes a proof-of-principle experiment of channel-resolved EWP interferometry based on SCI. Due to the limited momentum resolution in the distribution in Figure 6 we refrain from a more detailed analysis. In the future, however, we think that channel-resolved subcycle EWP interferometry can be applied to investigate the relation between strong-field-induced electron dynamics and the ensuing nuclear dynamics in molecules, similarly to channel-resolved ATI spectroscopy based on the ICI of EWPs[Reference Boguslavskiy, Mikosch, Gijsbertsen, Spanner, Patchkovskii, Gador, Vrakking and Stolow13].
$\text{H}_{2}$
, however, constitutes a proof-of-principle experiment of channel-resolved EWP interferometry based on SCI. Due to the limited momentum resolution in the distribution in Figure 6 we refrain from a more detailed analysis. In the future, however, we think that channel-resolved subcycle EWP interferometry can be applied to investigate the relation between strong-field-induced electron dynamics and the ensuing nuclear dynamics in molecules, similarly to channel-resolved ATI spectroscopy based on the ICI of EWPs[Reference Boguslavskiy, Mikosch, Gijsbertsen, Spanner, Patchkovskii, Gador, Vrakking and Stolow13].
4 Conclusion
In conclusion, we demonstrated a proof-of-principle experiment of channel-resolved interferometry based on SCI of EWPs released during strong field interaction of
![]() $\text{H}_{2}$
. We report on the observation of SCI in the strong field interaction of hydrogen molecules with cycle-shaped two-color laser fields. It is found that the structures corresponding to SCI are very sensitive to the shape of the two-color laser field cycle. Because ATD and ZPD of
$\text{H}_{2}$
. We report on the observation of SCI in the strong field interaction of hydrogen molecules with cycle-shaped two-color laser fields. It is found that the structures corresponding to SCI are very sensitive to the shape of the two-color laser field cycle. Because ATD and ZPD of
![]() $\text{H}_{2}^{+}$
can be distinguished by proton energy, channel-resolved electron momentum spectra could be obtained for the ionization and dissociation channels of
$\text{H}_{2}^{+}$
can be distinguished by proton energy, channel-resolved electron momentum spectra could be obtained for the ionization and dissociation channels of
![]() $\text{H}_{2}^{+}$
. In the future, the channel-resolved subcycle EWP interferometry demonstrated here can be employed for studies of multi-electron and multi-orbital effects in the laser-field-induced ionization and dissociation of molecules[Reference Boguslavskiy, Mikosch, Gijsbertsen, Spanner, Patchkovskii, Gador, Vrakking and Stolow13, Reference Xie, Doblhoff-Dier, Xu, Roither, Schöffler, Kartashov, Erattupuzha, Rathje, Paulus, Yamanouchi, Baltuška, Gräfe and Kitzler48, Reference Xie, Roither, Schöffler, Lötstedt, Kartashov, Zhang, Paulus, Iwasaki, Baltuška, Yamanouchi and Kitzler49].
$\text{H}_{2}^{+}$
. In the future, the channel-resolved subcycle EWP interferometry demonstrated here can be employed for studies of multi-electron and multi-orbital effects in the laser-field-induced ionization and dissociation of molecules[Reference Boguslavskiy, Mikosch, Gijsbertsen, Spanner, Patchkovskii, Gador, Vrakking and Stolow13, Reference Xie, Doblhoff-Dier, Xu, Roither, Schöffler, Kartashov, Erattupuzha, Rathje, Paulus, Yamanouchi, Baltuška, Gräfe and Kitzler48, Reference Xie, Roither, Schöffler, Lötstedt, Kartashov, Zhang, Paulus, Iwasaki, Baltuška, Yamanouchi and Kitzler49].
Acknowledgements
This research was financed by the Austrian Science Fund (FWF) under grants P25615-N27, P28475-N27, P21463-N22, P27491-N27 and SFB-F49 NEXTlite, and by a starting grant from the European Research Council (ERC project CyFi).