Attosecond twisted beams from high-order harmonic generation driven by optical vortices

Abstract

Optical vortices are structures of the electromagnetic field with a spiral phase ramp about a point-phase singularity, carrying orbital angular momentum (OAM). Recently, OAM has been imprinted to short-wavelength radiation through high-order harmonic generation (HHG), leading to the emission of attosecond twisted beams in the extreme-ultraviolet (XUV) regime. We explore the details of the mapping of the driving vortex to its harmonic spectrum. In particular, we show that the geometry of the harmonic vortices is convoluted, arising from the superposition of the contribution from the short and long quantum paths responsible of HHG. Finally, we show how to take advantage of transverse phase-matching to select twisted attosecond beams with different spatiotemporal properties.

1 Introduction

Twisted beams, also called optical vortices, exhibit a helical phase structure that imprints orbital angular momentum (OAM) to the beam, in addition to the spin angular momentum associated with the polarization^[1–3]. These singular beams, commonly generated in the optical spectral region, have potential technological applications in optical communication, micromanipulation, phase-contrast microscopy, among others^[4–7]. The production of twisted beams in the extreme-ultraviolet (XUV) and x-ray regimes is of great interest as it allows for the extension of the applications of optical vortices down to the nanometric scale. In this short-wavelength regime one can drastically reduce the diffraction limit, as well as exploit the selectively site-specific excitation, with an important impact in microscopy and spectroscopy^[8–14]. Several proposals have been explored in order to generate x-ray vortices in synchrotrons and FEL facilities^[15–18]. However, the generation of twisted beams carrying OAM in the x-ray regime is limited by the availability of efficient optical and diffractive elements.

In the last years, high-order harmonic generation (HHG) has been used to generate XUV vortices by imprinting the phase singularities in the infrared (IR) driving beam^{[13, 19, 20]}. HHG is a unique non-perturbative process, that combines microscopic and macroscopic physics to produce coherent XUV to soft x-ray radiation in the form of attosecond pulses^[21–25]. When an intense IR beam is focused into a gas target, the laser–matter interaction in each atom or molecule results in the emission of higher-order harmonics of the driving field. Microscopically, HHG can be understood with simple semiclassical arguments^{[26, 27]}: an electron is first tunnel-ionized from an atom, then accelerated in the continuum, and, due to the oscillatory behavior of the driving field, its recollision with the parent ion leads to the emission of higher-frequency radiation. Interestingly, there are two possible electronic quantum paths leading to the same kinetic energy at the recollision process – and thus to the same harmonic – known as short and long trajectories^{[28, 29]}. Macroscopically, the coherent addition of the radiation emitted from all the atoms in the target – also known as phase-matching^[30–32] – plays a relevant role for the efficient production of XUV/soft x-ray harmonics^{[30, 33]}. One can define longitudinal – or transverse – phase-matching as the interference of the harmonic emission emitted from different atoms in the target placed along the longitudinal or transverse direction^[34]. Transverse phase-matching is especially relevant in HHG driven by vortex beams due to their involved transverse field structure^[35].

If driven by pure vortex beams, the harmonic vortices are generated with a topological charge $\ell _{q}=q\ell$ ( $q$ being the harmonic order and $\ell$ the topological charge of the driver)^{[13, 20]}, and with similar divergence^{[13, 20, 36]}. As a consequence, several XUV highly charged harmonic vortices can by synthesized into twisted coherent attosecond beams, i.e., attosecond pulse trains delayed along the azimuthal beam coordinate. These beams, first predicted in Ref. [20], and recently measured in Ref. [36], arise as the superposition of several frequency beams with different OAM content^[37], and their spatiotemporal properties depend on phase-matching conditions^[35].

In this work we present a detailed theoretical analysis of the generation of twisted attosecond beams in the XUV regime. To this end, we analyze the phase-matching conditions in HHG driven by OAM beams, by means of two theoretical methods: the semiclassical thin slab model (TSM), and the 3D quantum model based on the strong field approximation (SFA) including propagation^[38]. We demonstrate that macroscopic phase-matching plays a relevant role to select OAM-HHG contributions from different quantum paths in the emission of XUV vortices. Finally, we show how to take advantage of transverse phase-matching to select twisted attosecond beams generated from different quantum-path contributions – and thus, exhibiting different spatiotemporal properties, – by changing the relative position between the driving beam focus and the gas jet.

2 Physical scenario of OAM-HHG

Before describing the theoretical methods, let us analyze the physical scenario of HHG driven by OAM beams. In Figure 1, we present a schematic view of the OAM-HHG scheme used in this work. A pulsed vortex beam centered at $\unicode[STIX]{x1D706}_{0}=800~\text{nm}$ , a typical wavelength used for HHG, is focused into an argon gas jet. High-order harmonics are emitted at each atom in the target, and, upon propagation, their coherent addition result in the far-field emission of XUV vortices, represented along the divergence $\unicode[STIX]{x1D6FD}$ and azimuth $\unicode[STIX]{x1D711}$ coordinates.

The spatial structure of the IR vortex beam is represented by a monochromatic Laguerre–Gaussian beam propagating in the $z$ -direction, with wavelength $\unicode[STIX]{x1D706}_{0}$ ( $k_{0}=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{0}$ ), expressed as $LG_{\ell ,p}(r,\unicode[STIX]{x1D719},z;k_{0})\text{e}^{\text{i}k_{0}z}$ where

(1) $$\begin{eqnarray}\displaystyle & & \displaystyle LG_{\ell ,p}(r,\unicode[STIX]{x1D719},z;k_{0})\nonumber\\ \displaystyle & & \displaystyle \quad =E_{0}\frac{w_{0}}{w(z)}\left(\frac{\sqrt{2}r}{w(z)}\right)^{\!|\ell |}L_{p}^{|\ell |}\!\left(\frac{2r^{2}}{w^{2}(z)}\right)\exp \left(-\frac{r^{2}}{w^{2}(z)}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \exp \left[\text{i}\ell \unicode[STIX]{x1D719}+\text{i}\frac{k_{0}r^{2}}{2R(z)}+\text{i}\unicode[STIX]{x1D6F7}_{G}(z)\right],\end{eqnarray}$$

and $w(z)=w_{0}\sqrt{1+(z/z_{0})^{2}}$ with $w_{0}$ is the waist of the mode, $z_{0}=k_{0}w_{0}^{2}/2$ the Rayleigh range, $R(z)=z[1+(z_{0}/z)^{2}]$ the phase-front radius, $\unicode[STIX]{x1D6F7}_{G}(z)=-(2p+|\ell |+1)\arctan (z/z_{0})$ the Gouy phase, and $L_{p}^{|\ell |}(x)$ the associated Laguerre polynomials

(2) $$\begin{eqnarray}\displaystyle L_{p}^{|\ell |}(x)=\mathop{\sum }_{m=0}^{p}(-1)^{m}\frac{(|\ell |+p)!}{(p-m)!\,(|\ell |+m)!\,m!}\,x^{m}. & & \displaystyle\end{eqnarray}$$

The indices $\ell =0,\pm 1,\pm 2,\ldots$ and $p=0,1,2,\ldots$ correspond to the topological charge and the number of nonaxial radial nodes of the mode, respectively. At the bottom of Figure 1 we present the amplitude (left) and phase (right) of the $LG_{1,0}$ IR mode. In the simulations presented in this work, we have considered as a driving field a well-defined OAM of $\ell =1$ , with a beam waist of $w_{0}=30~\unicode[STIX]{x03BC}\text{m}$ and, therefore, a Rayleigh range of $z_{0}=3.5~\text{mm}$ . The amplitude of the field $E_{0}$ is chosen to give a peak intensity of $1.4\times 10^{14}~\text{W}~\text{cm}^{-2}$ at the radii of maximum intensity of the $LG_{1,0}$ mode at the focal plane.

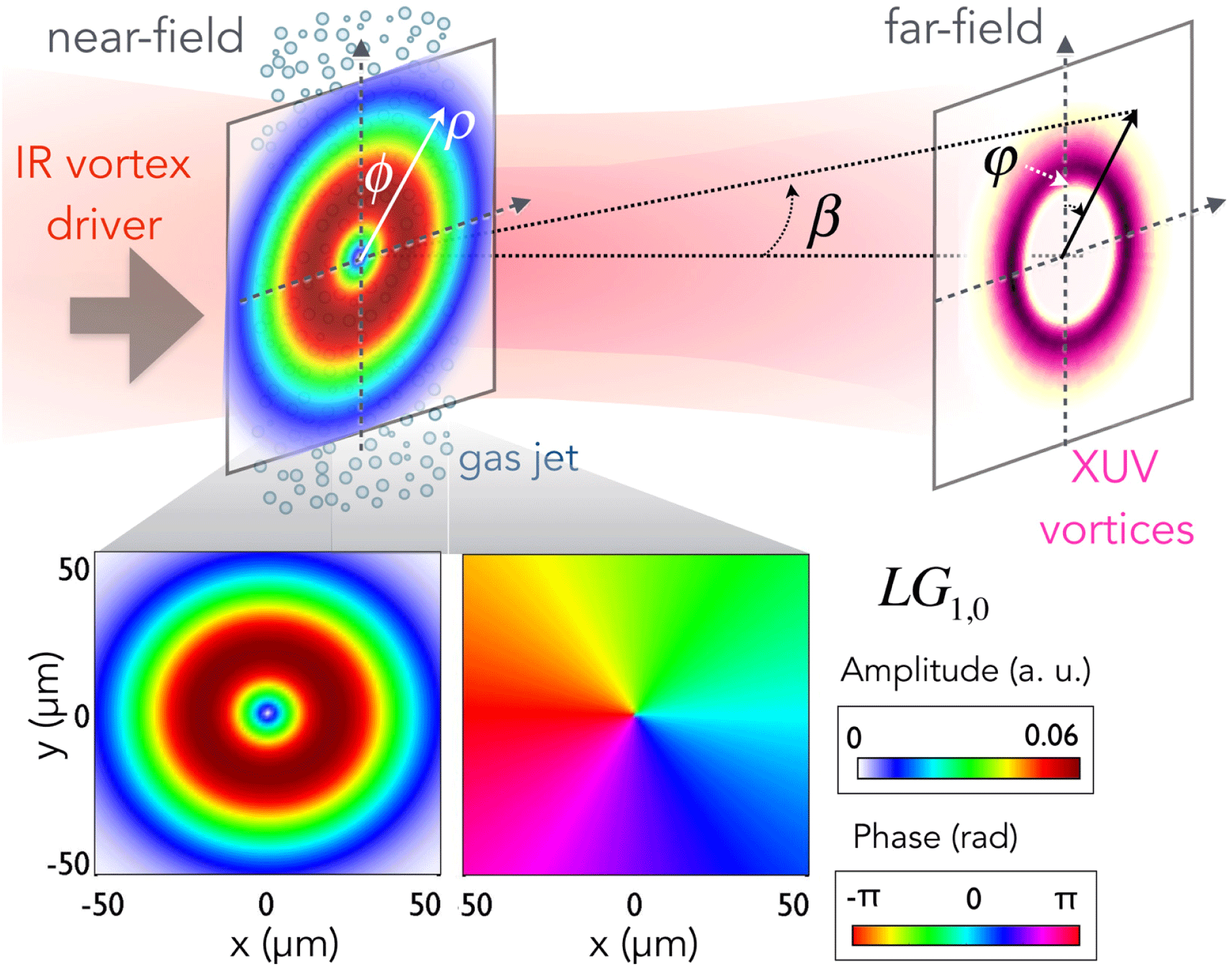
Figure 1. Schematic view of HHG driven by OAM beams. An intense IR vortex beam carrying OAM (with $\ell =1$ in this case), is focused into an argon gas jet. The near-field coordinates are ( $\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719}$ ). Each atom emits HHG radiation that, upon propagation, results in the far-field emission of XUV vortices with some divergence and azimuth ( $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D711}$ ). In the bottom we show the near-field amplitude (left) and phase (right) of the $LG_{1,0}$ IR mode, with beam waist of $30~\unicode[STIX]{x03BC}\text{m}$ .

3 Theoretical methods

Let us first present the two theoretical methods we use for the theoretical description of HHG driven by OAM beams. First, we present the semiclassical TSM that allows us to obtain an insight of the HHG process. Second, we present the 3D quantum SFA model, that gives a quantitative description of the process including both microscopic and macroscopic physics.

3.1 TSM

We have developed a semiclassical TSM – referred as quantum-path OAM model in Ref. [35] – that allows us to identify the physics of the XUV vortices generated via HHG. In this simplified description, the target is represented by a thin (2D) slab placed perpendicular to the propagation axis of the driving beam. This approach neglects the longitudinal phase-matching effects and allows us to focus the discussion on the transverse phase-matching^[34]. The driving beam profile in the thin slab, placed at $z=z_{t}$ , can be written as

(3) $$\begin{eqnarray}\displaystyle A(\mathbf{r})=U(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z_{t})\text{e}^{\text{i}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z_{t})}, & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D6F7}(\mathbf{r})$ contains the phase terms in the exponential of Equation (1), and the amplitude terms are grouped in $U(\mathbf{r})$ .

We consider the thin slab as a planar source of high-order harmonics, whose intensity profiles at the slab are related to that of the fundamental field. In the perturbative regime the amplitude of the generated radiation is proportional to the power of the fundamental beam amplitude, $\propto U(\mathbf{r})^{q}$ , where $q$ is the order of the emitted harmonic. However, since HHG is highly non-perturbative, the amplitude of the generated field scales with a lower power^[39]. Thus, the harmonic field at the slab can be approximated by an analytic SFA representation, first used in Ref. [40]. In this representation the amplitude of the $q$ th-harmonic is proportional to the $p$ th-power of the fundamental amplitude, $U(\mathbf{r})^{p}$ , where $p<q$ reflects the non-perturbative HHG behavior, being approximately constant for the harmonics in the plateau region. In our case we use $p=3.9$ ^{[35, 41]}. On the other hand, the phase of the harmonics scales with $q$ times the phase of the driving field, $q\unicode[STIX]{x1D6F7}(\mathbf{r})$ , and has an additional non-perturbative term, the intrinsic phase, which is proportional to the intensity of the fundamental field $\unicode[STIX]{x1D6FC}_{q}^{j}|U(\mathbf{r})|^{2}$ through the strong-field parameters $\unicode[STIX]{x1D6FC}_{q}^{j}$ , which depend on the electronic quantum path $(j)$ (short or long). They can be calculated from the action of classical trajectories with recollision energies leading to the considered harmonic^[30], and in our case we use $\unicode[STIX]{x1D6FC}_{19}^{S}=2.75\times 10^{-14}~\text{cm}^{2}~\text{W}^{-1}$ , and $\unicode[STIX]{x1D6FC}_{19}^{L}=2.220\times 10^{-13}~\text{cm}^{2}~\text{W}^{-1}$ , to reproduce the 19th harmonic. Thus, the contribution of the short $(S)$ and long $(L)$ quantum paths to the $q$ th-harmonic emitted at a slab located at $z_{t}$ can be written as

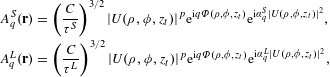(4) $$\begin{eqnarray}\displaystyle A_{q}^{S}(\mathbf{r}) & = & \displaystyle \left(\frac{C}{\unicode[STIX]{x1D70F}^{S}}\right)^{3/2}|U(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z_{t})|^{p}\text{e}^{\text{i}q\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z_{t})}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}_{q}^{S}|U(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z_{t})|^{2}},\nonumber\\ \displaystyle A_{q}^{L}(\mathbf{r}) & = & \displaystyle \left(\frac{C}{\unicode[STIX]{x1D70F}^{L}}\right)^{3/2}|U(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z_{t})|^{p}\text{e}^{\text{i}q\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z_{t})}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}_{q}^{L}|U(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},z_{t})|^{2}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

where $C$ is a constant and $\unicode[STIX]{x1D70F}^{S},\unicode[STIX]{x1D70F}^{L}$ are the excursion times associated with the short and long quantum paths, respectively^[28], affecting the efficiency of HHG due to the quantum diffusion of the electronic wavepacket.

Once we have the near-field description of the $q$ th-harmonic, we use Fraunhofer diffraction theory to calculate the far-field signal. The $q$ th-harmonic field at the divergence $(\unicode[STIX]{x1D6FD})$ and azimuthal $(\unicode[STIX]{x1D711})$ coordinates is given by

(5) $$\begin{eqnarray}\displaystyle F_{q}^{S}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D711}) & \propto & \displaystyle \int _{0}^{\infty }\!\int _{0}^{2\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D70C}^{\prime }\,\text{d}\unicode[STIX]{x1D70C}^{\prime }\,\text{d}\unicode[STIX]{x1D719}^{\prime }A_{q}^{S}(\mathbf{r}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,\text{e}^{-\text{i}(2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{q})\unicode[STIX]{x1D70C}^{\prime }\tan \unicode[STIX]{x1D6FD}\cos (\unicode[STIX]{x1D711}-\unicode[STIX]{x1D719}^{\prime })},\nonumber\\ \displaystyle F_{q}^{L}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D711}) & \propto & \displaystyle \int _{0}^{\infty }\!\int _{0}^{2\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D70C}^{\prime }\,\text{d}\unicode[STIX]{x1D70C}^{\prime }\,\text{d}\unicode[STIX]{x1D719}^{\prime }A_{q}^{L}(\mathbf{r}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,\text{e}^{-\text{i}(2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{q})\unicode[STIX]{x1D70C}^{\prime }\tan \unicode[STIX]{x1D6FD}\cos (\unicode[STIX]{x1D711}-\unicode[STIX]{x1D719}^{\prime })},\end{eqnarray}$$

where $(\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D719}^{\prime })$ represent the near-field polar coordinates, and $\unicode[STIX]{x1D706}_{q}$ is the wavelength of the $q$ th-harmonic related to the fundamental wavelength as $\unicode[STIX]{x1D706}_{q}=\unicode[STIX]{x1D706}_{0}/q$ . While this equation is valid for a driving field composed of any combination of Laguerre–Gaussian modes, let us now consider a driving field composed of a single OAM mode. In this case, the intensity of the driving does not vary along the azimuthal coordinate, i.e., $|U(\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D719}^{\prime },z_{t})|=|U(\unicode[STIX]{x1D70C}^{\prime },z_{t})|$ , and we can perform the analytic integral over $\unicode[STIX]{x1D719}^{\prime }$ . By considering the phase part of the fundamental Laguerre–Gaussian beam in Equation (1), we finally obtain^[35],

(6) $$\begin{eqnarray}\displaystyle F_{q}^{S}(\unicode[STIX]{x1D6FD}) & \propto & \displaystyle \left(\frac{C}{\unicode[STIX]{x1D70F}^{S}}\right)^{3/2}\int \unicode[STIX]{x1D70C}^{\prime }\,\text{d}\unicode[STIX]{x1D70C}^{\prime }|U(\unicode[STIX]{x1D70C}^{\prime },z_{t})|^{p}J_{q\ell }\left(\frac{2\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}_{q}}\unicode[STIX]{x1D6FD}~\unicode[STIX]{x1D70C}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\text{e}^{\text{i}q(k_{0}{\unicode[STIX]{x1D70C}^{\prime }}^{2}/2R(z_{t}))}\text{e}^{\text{i}q\unicode[STIX]{x1D6F7}_{G}(z_{t})}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}_{q}^{S}|U(\unicode[STIX]{x1D70C}^{\prime },z_{t})|^{2}},\nonumber\\ \displaystyle F_{q}^{L}(\unicode[STIX]{x1D6FD}) & \propto & \displaystyle \left(\frac{C}{\unicode[STIX]{x1D70F}^{L}}\right)^{3/2}\int \unicode[STIX]{x1D70C}^{\prime }\,\text{d}\unicode[STIX]{x1D70C}^{\prime }|U(\unicode[STIX]{x1D70C}^{\prime },z_{t})|^{p}J_{q\ell }\left(\frac{2\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}_{q}}\unicode[STIX]{x1D6FD}~\unicode[STIX]{x1D70C}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\text{e}^{\text{i}q(k_{0}{\unicode[STIX]{x1D70C}^{\prime }}^{2}/2R(z_{t}))}\text{e}^{\text{i}q\unicode[STIX]{x1D6F7}_{G}(z_{t})}\text{e}^{\text{i}\unicode[STIX]{x1D6FC}_{q}^{L}|U(\unicode[STIX]{x1D70C}^{\prime },z_{t})|^{2}}.\end{eqnarray}$$

Note that the detected harmonic signal will result from the superposition of short and long quantum-path contributions. We remark that Equation (6) is valid when the fundamental beam is composed by a single OAM mode. For any combination of different OAM modes, one should use Equation (5)^[41]. The TSM has been successfully validated against the 3D quantum SFA model for OAM-HHG calculations^{[35, 41]}.

3.2 3D quantum SFA simulation

In order to compute OAM-HHG including all quantum dynamics, we use our 3D quantum SFA method to compute HHG including both single-atom (microscopic) and propagation (macroscopic). We compute harmonic propagation using the electromagnetic field propagator^[38], where we assume the harmonic radiation to propagate with the vacuum phase velocity, which is a reasonable assumption for high-order harmonics. Propagation effects in the fundamental field, such as the production of free charges, the refractive index of the neutrals, the group velocity walk-off^[42], as well as absorption in the propagation of the harmonics, are also taken into account. In order to compute single-atom HHG, the exact calculation requires the integration of the time dependent Schrödinger equation. However, to ease the computational effort required to calculate propagation in a 3D geometry, the use of simplified models is almost mandatory. We use an extension of the standard SFA, hence we will refer it as SFA+, that shows an excellent agreement with the TDSE^[43].

One of the advantages of this method, that takes into account both microscopic and macroscopic HHG, is that is well-fitted to non-symmetric geometries; therefore, it is specially suited for computing HHG driven by beams carrying OAM^{[20, 35, 41]}.

4 Results

Once we have presented the physical scenario of OAM-HHG and the theoretical methods that we use, we analyze the simulation results. First, using the TSM, we will describe the OAM-HHG emission in terms of short and long quantum-path contributions, in order to identify the macroscopic conditions that allows us to separate them. Second, using the 3D quantum SFA model, we will analyze how the XUV vortices are emitted in the temporal domain, in order to macroscopically select attosecond twisted beams with different spatiotemporal properties.

4.1 Selecting different quantum-path contributions in OAM-HHG

The HHG spectrum results from the coherent addition of different quantum-path contributions. At the single-atom level, short and long quantum-path harmonic contributions are always present, although the later ones are less intense due to their longer excursion time. However, as they exhibit different harmonic phases, macroscopic phase-matching differs for each quantum-path contribution. As a consequence, different phase-matching conditions have been typically applied to macroscopically select the contributions from a single path. For example, when driving HHG by Gaussian beams, it is well known that if the gas jet is placed before the beam focus position, short quantum-path contributions dominate in the on-axis far-field profile. Moving to off-axis detection angles, long quantum-path contributions become prominent. In contrast, if the gas jet is placed after the focus position, short quantum-path contributions dominate the HHG spectrum over the whole far-field profile^{[31, 32]}. As a result, the relative position between the gas jet and the beam focus can be used to select quantum-path contributions, and thus to modify the temporal properties of the attosecond pulses emitted^[44]. Note that these phenomena has been successfully explained in terms of longitudinal phase-matching. In other words, the longitudinal phase variation along the gas jet, which depends strongly on the relative position between the Gaussian beam focus and the gas jet, favors the efficient emission of different quantum-path contributions. However, if HHG is driven by OAM beams, this behavior changes completely^[35], as we will discuss here in detail.

Here, with the help of our TSM we will disentangle the presence of short and long quantum-path contributions in HHG driven by OAM beams. As it has been done when driving HHG by Gaussian beams, in OAM-HHG we scan the relative position between the gas jet and the beam focus to modify the phase-matching conditions. Note that in the TSM, longitudinal phase-matching effects are neglected as a thin target is assumed. Thus, any macroscopic effect in the harmonic emission is unequivocally related to transverse phase-matching. In Figure 2, we show the results of the TSM for the 19th harmonic driven in argon. In the first row we show the far-field profile of the 19th harmonic obtained from the coherent addition of short and long quantum-path contributions. The thin slab is placed at different positions with respect to the beam focus ( $z=0$ ), from $z_{t}=-3~\text{mm}$ (left) to $z_{t}=3~\text{mm}$ (right). Different harmonic structures are obtained depending on the relative position between the gas jet and the focus. In order to identify the origin of those structures, we also present the results of the TSM considering only the short and long quantum-path contributions.

First, we observe that the yield of the short quantum-path contributions is more intense than the long ones, as expected form the shorter excursion time. Second, whereas the harmonic profiles from short quantum-path contributions are almost symmetric when placing the gas jet with respect to the focus position, those from the long contributions are completely asymmetric. For instance, in Figure 2(c), we can observe that if the gas jet is placed before the focus position $(z_{t}<0)$ long quantum-path contributions are more intense, and exhibit low divergence. On the other hand, if the gas jet is placed after the focus position $(z_{t}>0)$ long quantum-path contributions are substantially weaker and with higher divergence.

As a consequence, we can conclude that the emission of the 19th harmonic vortex shown in Figure 2(a) is dominated by the short quantum-path contributions except if the gas jet is placed before the focus position. In that case $(z_{t}<0)$ , short and long quantum-path contributions to the 19th harmonic exhibit similar intensity. In particular, in $z_{t}=-3~\text{mm}$ we can clearly distinguish a double vortex structure, where the inner part comes from the long quantum-path contributions, and the outer part from the short ones. We remark that these results, obtained using the TSM, are consequence of transverse phase-matching. Similar results were obtained when using thicker targets, indicating that in when using OAM beams, transverse phase-matching dominates over longitudinal phase-matching in HHG.

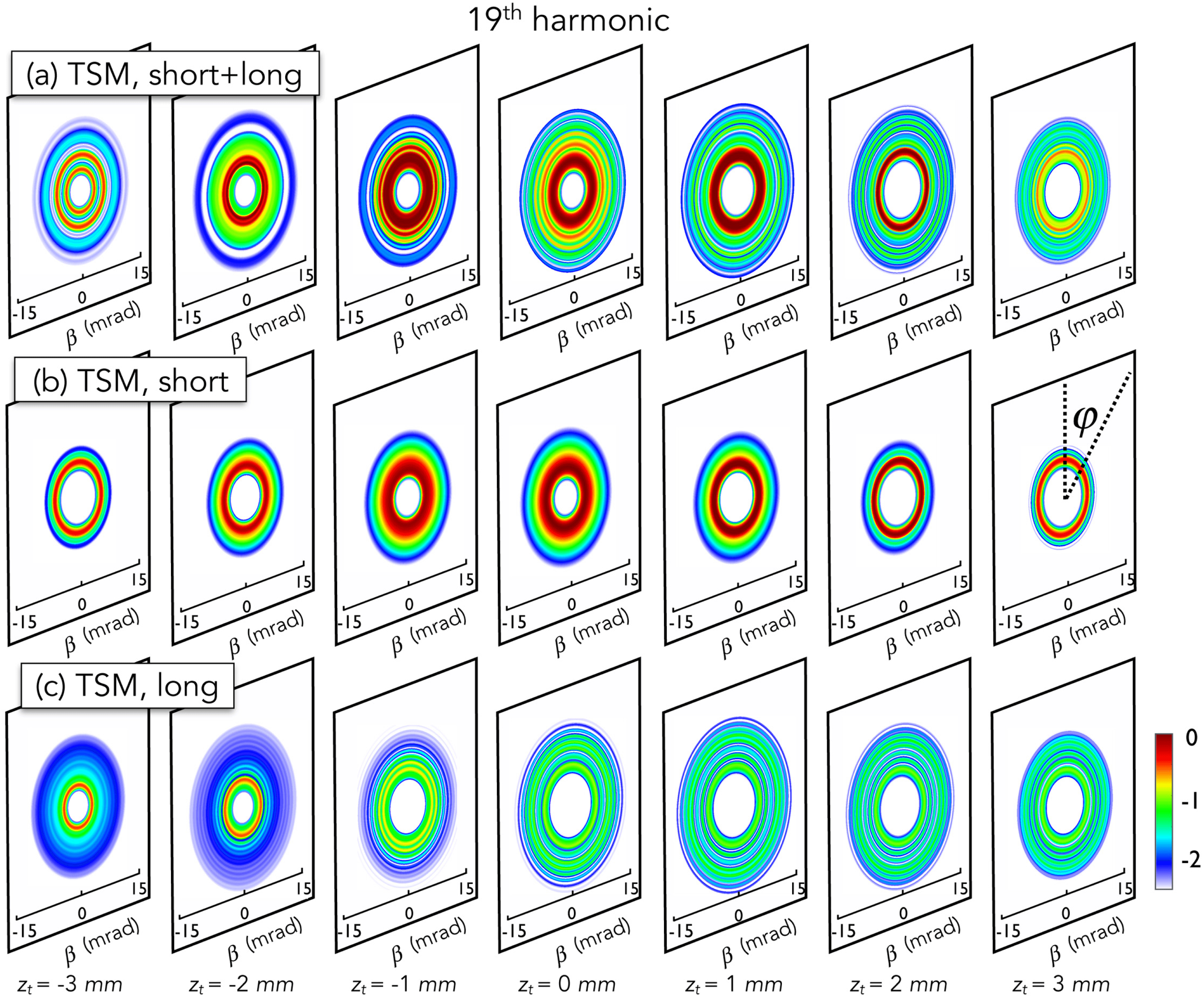
Figure 2. Spatial intensity profile of the emitted 19th harmonic for a slab placed at seven near-field positions, from $z_{t}=-3~\text{mm}$ (left) to $z_{t}=3~\text{mm}$ (right), calculated with the TSM considering (a) short $+$ long, (b) short and (c) long quantum-path contributions. Whereas short quantum-path contributions exhibit similar intensity and structure independently of the near-field slab location, long ones are more intense if the slab is placed before the focus position. As a consequence, a rich vortex structure profile is obtained depending on the relative position between the gas jet and the beam focus.

Figure 3. Radial intensity profile of the emitted 19th harmonic as a function of the near-field slab position, calculated with the TSM considering (a) short $+$ long, (b) short and (c) long quantum-path contributions. As depicted in Figure 2, the dependence of the profile of short quantum-path contributions with the slab position is almost symmetric with respect to the focus, whereas that of the long ones is completely asymmetric. As a consequence, the relative position between the gas jet and the beam focus serves as a knob control to select harmonic vortices with short or long quantum-path contributions.

For illustration purposes we present in Figure 3, the radial profile intensity of the 19th harmonic as a function of the slab position using the TSM an accounting for short  $+$ long, short and long quantum-path contributions. As depicted in Figure 2, the dependence of the radial profile of short quantum-path contributions with the slab position is almost symmetric with respect to the focus. However, in the case of long quantum-path contributions that dependence is asymmetric, being more intense and less divergent if the slab is placed before the focus position. As a consequence, we demonstrate that the relative position between the gas jet and the beam focus serves as a knob control to select harmonic vortices with short or long quantum-path contributions.

Figure 4. Attosecond twisted beam structures of the emitted harmonic radiation obtained with the 3D SFA quantum model for a multi-cycle driving laser pulse of $\unicode[STIX]{x1D70F}_{P}=15.4~\text{fs}$ (a, b) and a few-cycle driver of $\unicode[STIX]{x1D70F}_{P}=3.8~\text{fs}$ (c, d). The harmonics are generated in a $500~\unicode[STIX]{x03BC}\text{m}$ argon gas jet placed 2 mm before (a, c) and after (b, d) the focus position. On the left we show the attosecond twisted beam structure, whereas on the right we show transverse intensity snapshots at four different time instants within a half-cycle, $0.12T,0.25T,0.38T$ and $0.5T$ (where $T$ is the laser period). The contribution from long quantum-path contributions is indicated in yellow.

4.2 Attosecond twisted beams

Harmonic vortices generated through OAM-HHG exhibit similar far-field divergence. This result, that has been observed both theoretically^{[20, 35]} and experimentally^{[13, 19, 36]}, is a consequence of the simple OAM build-up rule $\ell _{q}=q\ell$ ^[36]. This allows us to synthesize several harmonic vortices, each of them with different topological charge $\ell _{q}$ . As a result, an attosecond twisted beam^[20], also called light spring ^[37] is obtained. This structure can be interpreted as an attosecond pulse train that is delayed along the azimuthal coordinate according to the spatial phase of the fundamental OAM beam. Here we will take advantage of the macroscopic conditions described before to generate attosecond helical beams whose main contribution comes from short or long quantum paths.

To this end, we use the 3D quantum SFA model. The driving laser beam, spatially represented as an $LG_{1,0}$ mode, is modeled temporally with a $sin^{2}$ temporal envelope with pulse duration $\unicode[STIX]{x1D70F}_{p}$ (intensity full-width-half-maximum). The 3D gas jet is directed along the $x$ -axis, and modeled by a Gaussian distribution along the $y$ and $z$ dimensions (whose FWHM is $500~\unicode[STIX]{x03BC}\text{m}$ ), and a constant profile along its axial dimension, $x$ , with a peak density of $10^{17}~\text{atoms}~\text{cm}^{-3}$ .

In Figure 4, we show first the attosecond twisted beams driven by a multi-cycle laser pulse with $\unicode[STIX]{x1D70F}_{p}=15.4~\text{fs}$ (5.8 cycles), in a gas jet centered at $z_{t}=-2~\text{mm}$ and $z_{t}=2~\text{mm}$ . On the left we show the attosecond helical beam structure, whereas on the right we show transverse intensity snapshots at four different time instants within a half-cycle. Note that an Al filter (250 nm thick) has been used to filter out the low-order harmonics (below the 11th). The remaining harmonic beam is thus composed of harmonics from 13th to 27th. When the gas jet is placed before the focus we can distinguish two attosecond beam structures, which can be identified as coming from the long (yellow) and short (purple) quantum-path contributions, accordingly to what was observed in the previous section. In addition, at the different snapshots we observe an inner part structure (indicated by the yellow arrows) that comes from the long quantum-path contributions. Note that this structure is delayed in time with respect to the main structure, thus in agreement with the knowledge of HHG, where long quantum paths are emitted after the short ones. On the other hand, if the gas jet is placed after the focus position, short quantum-path contributions dominate. Note that the emission of short and long quantum-path contributions exhibit opposite harmonic chirp^[45]. As a consequence, we have shown that by selecting appropriate macroscopic conditions we can obtain helical attosecond beams with different spatial and temporal properties.

Finally, we show the attosecond twisted beams driven by a few-cycle laser pulse $(\unicode[STIX]{x1D70F}_{p}=3.8~\text{fs})$ . As in the case of the longer driver, when the gas jet is placed 2 mm before the focus, two well-defined structures from long (yellow) and short (purple) quantum-path contributions are obtained. For instance it can be observed that the attosecond helical beam from long quantum-path contributions is delayed in time with respect to the short one. On the other hand, if the gas jet is placed 2 mm after the focus position, short quantum-path trajectories dominate. Note that in both cases, the attosecond helical beam driven by a few-cycle laser beam can be used as a carrier-envelope-phase map of the driver field into the XUV harmonics along the azimuthal coordinate.

5 Conclusions and outlook

We have presented a detailed analysis of the macroscopic synthesis of attosecond twisted beams. With the help of a semiclassical TSM of OAM-HHG and the 3D quantum SFA simulations, we identify the adequate phase-matching conditions to disentangle the short and long quantum-path contributions in HHG driven by optical vortices. In particular, we have shown that by modifying the relative position between the gas jet and the beam focus, we can obtain twisted attosecond beams with different spatial and temporal properties.

Our results open an exciting perspective for the application of attosecond twisted beams. First, we note that although we have reported harmonic vortices in the XUV regime, their energy content could be extended towards the soft x-rays if driving beams with longer, mid-IR^[33], or shorter, ultraviolet^[46] wavelengths were used in HHG, or by using other scenarios, such as plasmas^[47–49], solid targets^{[50, 51]}, or free electron laser facilities^[52]. In the attosecond twisted beams both the phase and the intensity profile exhibit a helical structure. Thus, they are perfect candidates to exchange OAM in situations where not only the phase possesses a helical structure (like standard OAM beams), opening an entire new light–matter interaction regime. New regimes, in which the non-perturbative behavior of HHG imprints a relevant signature in the generated attosecond twisted beams^[41], or where harmonics with both OAM and spin angular momentum are generated^[53], remain to be explored.