1 Introduction
In laser driven inertial confinement fusion[Reference Lindl, Amedt, Berger, Glendinning, Glenzer, Hann, Landen and Suter1, Reference Bodner, Colomant, Gardner, Lehmberg, Obenschain, Phillips, Schmitt, Sethian, McCrory, Seka, Verdon, Knauer, Afeyan and Powell2], the optical spectrum is broadened for two purposes, one is to avoid the stimulated Brillouin scattering in the large aperture optics[Reference Murray, Smith, Ehrlich, Kyrazis, Thompson, Weiland and Wilcox3], and the other is to ‘smooth’ the speckle pattern of beam on the target combined with the spectral dispersion (SSD) method[Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures4–Reference Zuegel, Jacobs-Perkins, Marozas, Roides, Bittle, MIchaels, Regan, Craxton, Kelly, Kessler, Seka and Skupsky6]. Phase modulation is the current method to broaden the optical spectrum (also called the frequency modulation (FM))[Reference Liao, Zhou and Meng7, Reference Hocquet, Penninckx, Gleyze, Gouedard and Jaouen8]. Ideally, the pure phase modulation will not change the beam intensity. However, if the optical spectral transmission is nonuniform in propagation, the FM would convert to the amplitude modulation (AM)[Reference Rothenberg, Browning and Wilcox9, Reference Hocquet, Penninckx, Bordenave, Gouedard and Jaouen10]. The AM needs to be reduced or at least controlled for two reasons. First, it is a main difficulty in controlling temporal shape to ensure an optimal interaction of laser–target[Reference Lindl, Amedt, Berger, Glendinning, Glenzer, Hann, Landen and Suter1, Reference Bodner, Colomant, Gardner, Lehmberg, Obenschain, Phillips, Schmitt, Sethian, McCrory, Seka, Verdon, Knauer, Afeyan and Powell2]. Second, the intensity peaks due to the AM might damage optics and hence depress laser performance[Reference Bespalov and Talanov11–Reference Zheng, Ma, Li, Liu and Chen13]. The common basis for all effects is the nonuniform spectral transmission[Reference Rothenberg, Browning and Wilcox9]. Etalon effect is an important factor that causes spectral transmission distortion because the number of transmissive optics is large and optics coating would degrade during long term operation in high-power laser facility[Reference Xu, Wang, Li, Lin, Zhang, Deng, Deng, Huang, Wang, Ding and Tang14, Reference Ling, Zhao, Li, Shao and Fan15].
Typically SSD beam contains an optical fiber phase modulation that imposes bandwidth in the front-end system and an SSD grating that disperses the broadband beam in the pre-amplifier system[Reference Jolly, Gleyze, Penninckx, Beck, Videau and Coic16, Reference Spaeth, Manes, Kalantar, Miller, Heebner, Bliss, Speck, Parham, Whitman, Wegner, Baisden, Menapace, Bowers, Cohen, Suratwala, Di Nicola, Newton, Adams, Trenholme, Finucane, Bonanno, Rardin, Arnold, Dixit, Erbert, Erlandson, Fair, Feigenbaum, Gourdin, Hawley, Honig, House, Jancaitis, LaFortune, Larson, Le Galloudec, Lindl, MacGowan, Marshall, McCandless, McCracken, Montesanti, Moses, Nostrand, Pryatel, Roberts, Rodriguez, Rowe, Sacks, Salmon, Shaw, Sommer, Stolz, Tietbohl, Widmayer and Zacharias17]. Compared with traditional broadband beam, phase modulation or SSD beam is very special for its monochromatic feature at given time and space[Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures4]. The traditional method using optical spectral transfer function as filters to analyze the FM-to-AM conversion is therefore insufficient to describe the AM characteristics of SSD beam. Since the AM in near field is associated with laser nonlinear effect and laser damage of optics[Reference Bespalov and Talanov11], in far field it affects the laser–target interaction[Reference Lindl, Amedt, Berger, Glendinning, Glenzer, Hann, Landen and Suter1], and in partial area sampled from near field impacts pulse measurement and precision control[Reference Li, Jing, Wu, Zhao, Li, Lin and Su18]. It is necessary to obtain the complete AM characteristics for its importance on above-mentioned aspects.
In this paper, we theoretically investigate the AM characteristic of SSD beam induced by the etalon effect in high-power laser facility. With a low-order approximation, the analytic model of temporal shape intensity is obtained for the first time, which gives the detailed AM phenomenon and rules of shaped SSD pulse at local and integral aspects.
2 Theoretical analysis of etalon effect in transmission plate
When a beam passes through a transmission plate, with thickness
![]() $d$
and residual reflectivity
$d$
and residual reflectivity
![]() $R$
, as shown in Figure 1, the number of reflections approaches infinite: in one cycle, the forward beam in the plate is split into two beams at the output interface and the reflected part will be reflected again at the input interface. As a result, it goes forward as the initial forward beam in the plate in the next cycle.
$R$
, as shown in Figure 1, the number of reflections approaches infinite: in one cycle, the forward beam in the plate is split into two beams at the output interface and the reflected part will be reflected again at the input interface. As a result, it goes forward as the initial forward beam in the plate in the next cycle.
According to the reflection process, the delay time of the
![]() $m$
-order output is obtained by
$m$
-order output is obtained by
In the calculation, the change of the refractive index with the optical wavelength of SSD beam is ignored due to the beam’s small bandwidth. The output optical field contains amplitude attenuation and a phase delay. Considering these two aspects, the
![]() $m$
-order optical field transmission is given by
$m$
-order optical field transmission is given by
The total output is a summation of the infinite series that comes from the multi-times reflection in the plate and given by
where
![]() $A_{\text{in}}(t)$
and
$A_{\text{in}}(t)$
and
![]() $A_{\text{out}}(t)$
are the input and output amplitudes of the optical field, respectively. When the steady-state approximation, which is a traditional method used in the Fabry–Perot (F–P) etalon, is applied to solve Equation (3), the output optical amplitude can be derived as
$A_{\text{out}}(t)$
are the input and output amplitudes of the optical field, respectively. When the steady-state approximation, which is a traditional method used in the Fabry–Perot (F–P) etalon, is applied to solve Equation (3), the output optical amplitude can be derived as
And the intensity is calculated as
Equation (5) is the standard spectral transmission function of the F–P etalon. Generally, steady-state approximation is not satisfied in high-power laser facility due to the sharply shaped pulse which would cause inaccurate solutions. Since
![]() $R$
is a small quantity in high-power laser facility thus the
$R$
is a small quantity in high-power laser facility thus the
![]() $|T_{m+1}|/|T_{m}|\ll 1$
, one can use the low-order approximation to solve Equation (3). We get the first two terms of Equation (3) and calculate the output optical amplitude
$|T_{m+1}|/|T_{m}|\ll 1$
, one can use the low-order approximation to solve Equation (3). We get the first two terms of Equation (3) and calculate the output optical amplitude
Let us consider a typical SSD beam that the dispersion direction is along
![]() $x$
-axis. Then the time–space optical field distribution can be written as
$x$
-axis. Then the time–space optical field distribution can be written as
where
![]() $A_{0}(t,x)$
is the pulse amplitude, and
$A_{0}(t,x)$
is the pulse amplitude, and
![]() $\unicode[STIX]{x1D714}_{0}$
and
$\unicode[STIX]{x1D714}_{0}$
and
![]() $\unicode[STIX]{x1D714}$
are the central and modulation angular frequency, respectively.
$\unicode[STIX]{x1D714}$
are the central and modulation angular frequency, respectively.
![]() $\unicode[STIX]{x1D6FF}$
is the modulation depth,
$\unicode[STIX]{x1D6FF}$
is the modulation depth,
![]() $k$
is the dispersion parameter and the value is
$k$
is the dispersion parameter and the value is
![]() $2\unicode[STIX]{x1D70B}N_{c}/D$
,
$2\unicode[STIX]{x1D70B}N_{c}/D$
,
![]() $N_{c}$
is the number of color cycles and
$N_{c}$
is the number of color cycles and
![]() $D$
is the beam aperture. Substituting Equation (7) into Equation (6), we can obtain the output optical field as
$D$
is the beam aperture. Substituting Equation (7) into Equation (6), we can obtain the output optical field as
 $$\begin{eqnarray}\displaystyle E_{\text{out}}(t,x) & = & \displaystyle (1-R)A_{0}\left(t-\frac{nd}{c}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,e^{i\unicode[STIX]{x1D714}_{0}(t-nd/c)}e^{i\unicode[STIX]{x1D6FF}\sin \left[\unicode[STIX]{x1D714}\left(t-nd/c\right)+kx\right]}\nonumber\\ \displaystyle & & \displaystyle +\,(1-R)RA_{0}\left(t-\frac{3nd}{c}\right)e^{i\unicode[STIX]{x1D714}_{0}(t-3nd/c)}\nonumber\\ \displaystyle & & \displaystyle \times \,e^{i\unicode[STIX]{x1D6FF}\sin [\unicode[STIX]{x1D714}(t-3nd/c)+kx]}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{\text{out}}(t,x) & = & \displaystyle (1-R)A_{0}\left(t-\frac{nd}{c}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,e^{i\unicode[STIX]{x1D714}_{0}(t-nd/c)}e^{i\unicode[STIX]{x1D6FF}\sin \left[\unicode[STIX]{x1D714}\left(t-nd/c\right)+kx\right]}\nonumber\\ \displaystyle & & \displaystyle +\,(1-R)RA_{0}\left(t-\frac{3nd}{c}\right)e^{i\unicode[STIX]{x1D714}_{0}(t-3nd/c)}\nonumber\\ \displaystyle & & \displaystyle \times \,e^{i\unicode[STIX]{x1D6FF}\sin [\unicode[STIX]{x1D714}(t-3nd/c)+kx]}.\end{eqnarray}$$
In Equation (8), the time–space optical field has theoretical expression; therefore, AM can be calculated directly in time domain instead of using optical spectrum transfer function to describe FM-to-AM conversion of etalon effect.
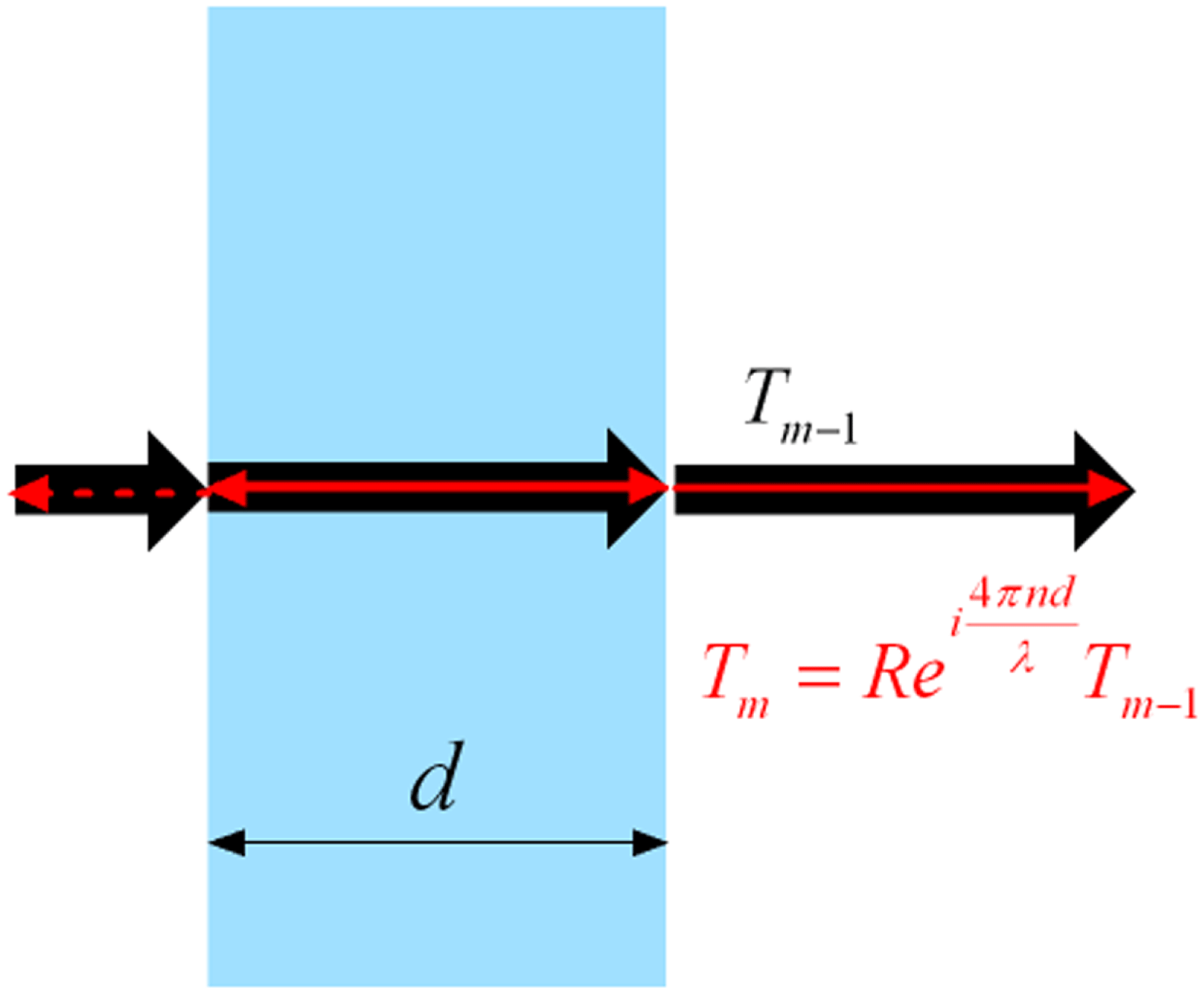
Figure 1. Schematic representation of the beam mixing process in transmission plate.
3 AM of SSD beam induced by etalon effect in near field
For single sinusoidal phase modulation, the temporal intensity of output optical field is calculated from Equation (8) as
In Equation (9), the parameters
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x1D6F7}(t,x)$
are extracted by
$\unicode[STIX]{x1D6F7}(t,x)$
are extracted by
and
where
![]() $a=2\unicode[STIX]{x1D6FF}\sin (\unicode[STIX]{x1D714}nd/c)$
and
$a=2\unicode[STIX]{x1D6FF}\sin (\unicode[STIX]{x1D714}nd/c)$
and
![]() $\unicode[STIX]{x1D711}_{0}=2n\unicode[STIX]{x1D714}_{0}d/c$
. The output pulse intensity as shown in Equation (9) has a cosine function term that accounts for the AM of SSD beam; the modulus and the phase of the cosine function determine the amplitude and patterns of AM.
$\unicode[STIX]{x1D711}_{0}=2n\unicode[STIX]{x1D714}_{0}d/c$
. The output pulse intensity as shown in Equation (9) has a cosine function term that accounts for the AM of SSD beam; the modulus and the phase of the cosine function determine the amplitude and patterns of AM.
With the definition of the FM-to-AM conversion factor[Reference Hocquet, Penninckx, Bordenave, Gouedard and Jaouen10], the distortion criterion
![]() $\unicode[STIX]{x1D6FC}$
is calculated as
$\unicode[STIX]{x1D6FC}$
is calculated as
It indicates that the distortion criterion is proportional to
![]() $R$
and
$R$
and
![]() $\unicode[STIX]{x1D702}$
.
$\unicode[STIX]{x1D702}$
.
![]() $R$
is a constant parameter related to the plate property,
$R$
is a constant parameter related to the plate property,
![]() $\unicode[STIX]{x1D702}$
is impacted by the pulse temporal shape expressed by Equation (10). We can easily obtain that the distortion criterion is reduced at the position where pulse has a sharp rise.
$\unicode[STIX]{x1D702}$
is impacted by the pulse temporal shape expressed by Equation (10). We can easily obtain that the distortion criterion is reduced at the position where pulse has a sharp rise.
Equation (9) obviously shows that the time-varying AM patterns have the same period as FM. In order to obtain the detailed AM patterns, we performed a modulo-
![]() $\unicode[STIX]{x1D70B}$
operation on the phase function and quantized the results into discrete phase levels with the name equivalent phase.
$\unicode[STIX]{x1D70B}$
operation on the phase function and quantized the results into discrete phase levels with the name equivalent phase.
![]() $\unicode[STIX]{x1D6F7}(t,x)$
is accordingly converted into equivalent phases to analyze the AM patterns, and it indicates that the values of
$\unicode[STIX]{x1D6F7}(t,x)$
is accordingly converted into equivalent phases to analyze the AM patterns, and it indicates that the values of
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $a$
(the half variation range of
$a$
(the half variation range of
![]() $\unicode[STIX]{x1D6F7}(t,x)$
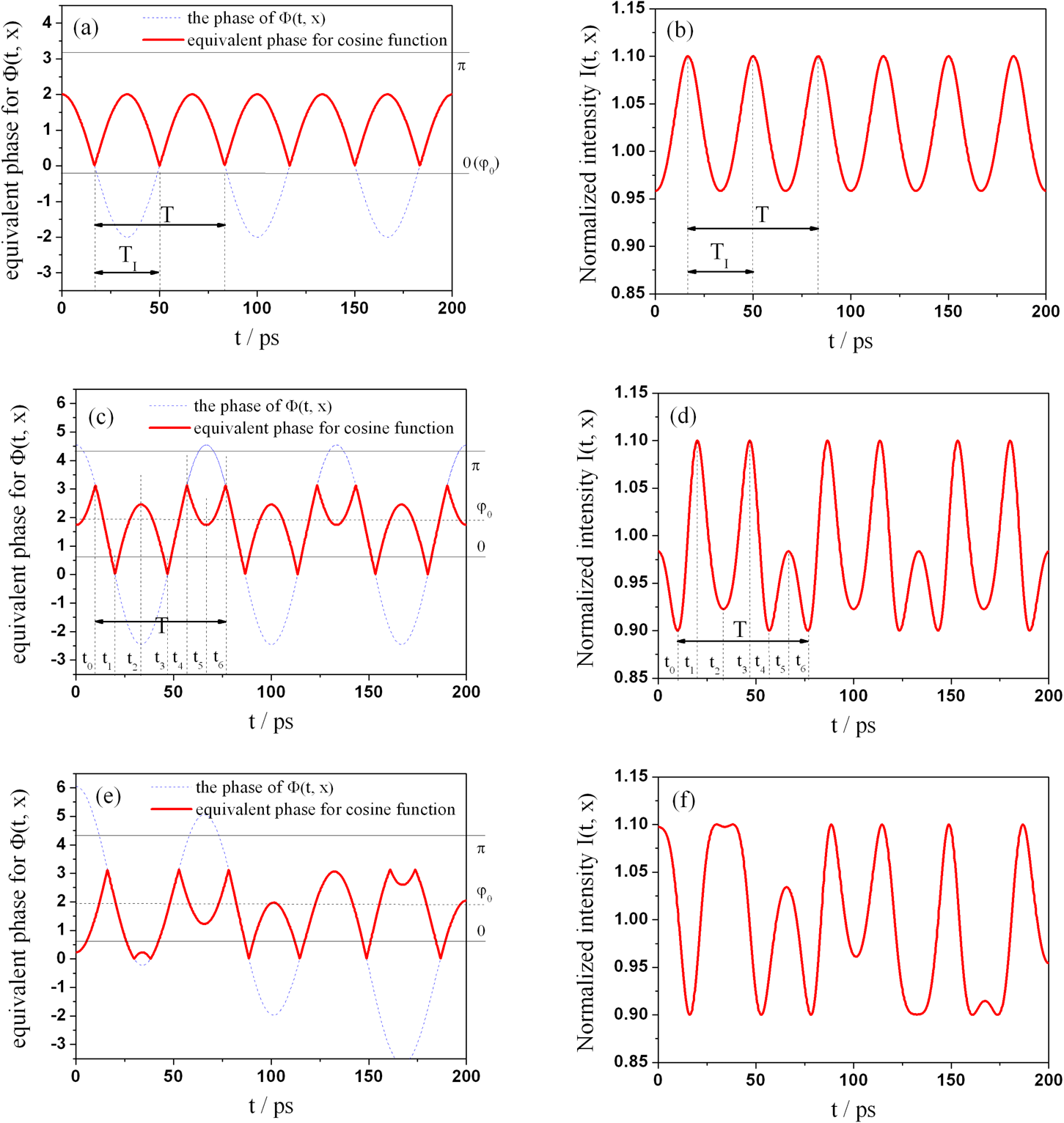
) are key points to impact AM patterns. Figures 2 shows some examples of the equivalent phases (Figures 2(a), 2(c) and 2(e)) and the corresponding AM patterns (Figures 2(b), 2(d) and 2(f)). For clear comparisons, we classify our discussion into two cases as follows.
$\unicode[STIX]{x1D6F7}(t,x)$
) are key points to impact AM patterns. Figures 2 shows some examples of the equivalent phases (Figures 2(a), 2(c) and 2(e)) and the corresponding AM patterns (Figures 2(b), 2(d) and 2(f)). For clear comparisons, we classify our discussion into two cases as follows.
(1) When
 $\unicode[STIX]{x1D711}_{0}$
satisfies the condition
$\unicode[STIX]{x1D711}_{0}$
satisfies the condition
 $\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}$
(
$\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}$
(
 $n_{0}$
is an integer, the same below), the term
$n_{0}$
is an integer, the same below), the term
 $\cos \unicode[STIX]{x1D6F7}(t,x)$
from Equation (9) can be simplified as
$\cos \unicode[STIX]{x1D6F7}(t,x)$
from Equation (9) can be simplified as
 $\cos \{a\cos [\unicode[STIX]{x1D714}(t-2nd/c)+kx]\}$
, which has two uniform types in a period and the AM period is reduced to half, which is shown in Figures 2(a) and 2(b). Supposing the FM period is
$\cos \{a\cos [\unicode[STIX]{x1D714}(t-2nd/c)+kx]\}$
, which has two uniform types in a period and the AM period is reduced to half, which is shown in Figures 2(a) and 2(b). Supposing the FM period is
 $T$
, the actual period
$T$
, the actual period
 $T_{1}$
can be easily obtained as
$T_{1}$
can be easily obtained as
 $T_{1}=T/2$
.
$T_{1}=T/2$
.(2) When
 $\unicode[STIX]{x1D711}_{0}$
is not
$\unicode[STIX]{x1D711}_{0}$
is not
 $2\unicode[STIX]{x1D70B}n_{0}$
, AM patterns may have multiple ripples with different amplitudes and widths in a period. As shown in Figures 2(c) and 2(d), there are three different ripples. Additionally, if the value of
$2\unicode[STIX]{x1D70B}n_{0}$
, AM patterns may have multiple ripples with different amplitudes and widths in a period. As shown in Figures 2(c) and 2(d), there are three different ripples. Additionally, if the value of
 $a$
is bigger, the number of ripples in one period is larger. This phenomenon can be easily mistaken for random noise in high-power laser facility.
$a$
is bigger, the number of ripples in one period is larger. This phenomenon can be easily mistaken for random noise in high-power laser facility.
We analyzed the values of
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $a$
with typical SSD parameters. That is,
$a$
with typical SSD parameters. That is,
![]() $\unicode[STIX]{x1D6FF}=2$
,
$\unicode[STIX]{x1D6FF}=2$
,
![]() $\unicode[STIX]{x1D714}=2\unicode[STIX]{x1D70B}f=30\unicode[STIX]{x1D70B}~\text{GHz}$
,
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x1D70B}f=30\unicode[STIX]{x1D70B}~\text{GHz}$
,
![]() $n=1.5$
, and
$n=1.5$
, and
![]() $\unicode[STIX]{x1D714}_{0}=1.8\times 10^{15}(1053~\text{nm})$
. The results are
$\unicode[STIX]{x1D714}_{0}=1.8\times 10^{15}(1053~\text{nm})$
. The results are
![]() $\unicode[STIX]{x1D711}_{0}=1.8\times 10^{7}d$
and
$\unicode[STIX]{x1D711}_{0}=1.8\times 10^{7}d$
and
![]() $a=2\unicode[STIX]{x1D6FF}\sin (\unicode[STIX]{x1D714}nd/c)$
.
$a=2\unicode[STIX]{x1D6FF}\sin (\unicode[STIX]{x1D714}nd/c)$
.
![]() $\unicode[STIX]{x1D711}_{0}$
changes linearly with the plate thickness, while the large slope coefficient indicates that the plate thickness is very sensitive. Generally, in high-power laser facility,
$\unicode[STIX]{x1D711}_{0}$
changes linearly with the plate thickness, while the large slope coefficient indicates that the plate thickness is very sensitive. Generally, in high-power laser facility,
![]() $\unicode[STIX]{x1D711}_{0}$
around
$\unicode[STIX]{x1D711}_{0}$
around
![]() $2\unicode[STIX]{x1D70B}n_{0}$
has low probability to occur,
$2\unicode[STIX]{x1D70B}n_{0}$
has low probability to occur,
![]() $a$
is periodically varied with the plate thickness and it indicates that the plate thickness can be precisely designed to reduce the ripples’ number and amplitude.
$a$
is periodically varied with the plate thickness and it indicates that the plate thickness can be precisely designed to reduce the ripples’ number and amplitude.
For multiple sinusoidal phase modulations, the temporal shape is calculated as
 $$\begin{eqnarray}\displaystyle I(t,x) & = & \displaystyle (1-R)^{2}\left|A_{0}\left(t-\frac{nd}{c}\right)\right|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\vphantom{\frac{2n\unicode[STIX]{x1D714}_{0}d}{c}}1+2R\unicode[STIX]{x1D702}\cos \left[\vphantom{\frac{2n\unicode[STIX]{x1D714}_{0}d}{c}}a_{1}\cos \unicode[STIX]{x1D6F7}_{1}(t,x)\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.a_{2}\cos \unicode[STIX]{x1D6F7}_{2}(t,x)+\frac{2n\unicode[STIX]{x1D714}_{0}d}{c}\right]\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(t,x) & = & \displaystyle (1-R)^{2}\left|A_{0}\left(t-\frac{nd}{c}\right)\right|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\vphantom{\frac{2n\unicode[STIX]{x1D714}_{0}d}{c}}1+2R\unicode[STIX]{x1D702}\cos \left[\vphantom{\frac{2n\unicode[STIX]{x1D714}_{0}d}{c}}a_{1}\cos \unicode[STIX]{x1D6F7}_{1}(t,x)\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.a_{2}\cos \unicode[STIX]{x1D6F7}_{2}(t,x)+\frac{2n\unicode[STIX]{x1D714}_{0}d}{c}\right]\right\}.\end{eqnarray}$$
The distortion criterion of AM has the same value as one sinusoidal phase modulation, but AM patterns are more complex, as shown in Figures 2(e) and 2(f). The traditional periodical pattern disappeared and the amplitude and the width of ripples varied over entire pulse.
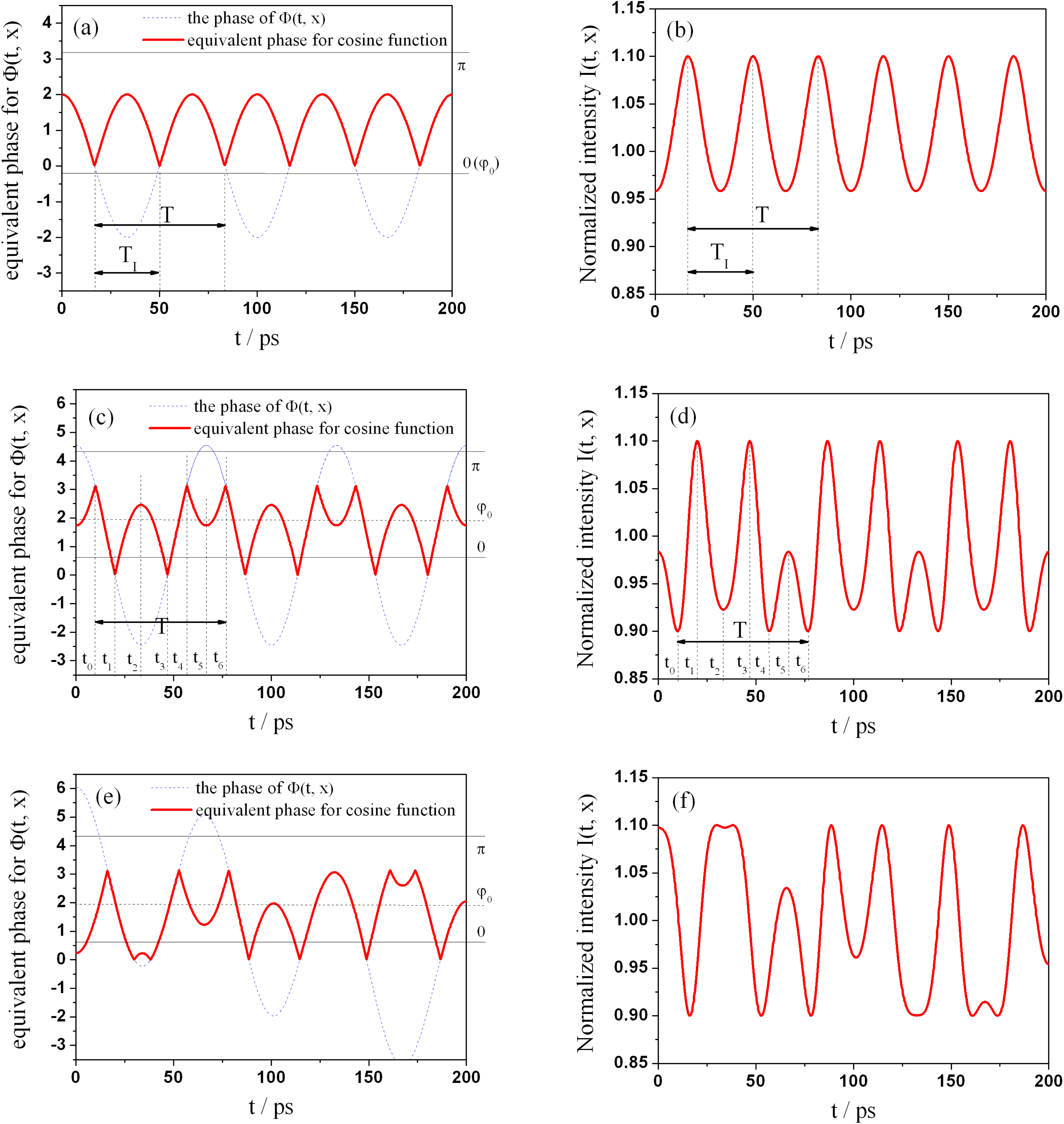
Figure 2. Samples of equivalent phases and the corresponding AM patterns of SSD beam induced by etalon effect. In the left three figures, red curves and blue curves denote the equivalent phase and the original phase, respectively. The parameters are (a) one sinusoidal phase modulation with
![]() $\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}$
,
$\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}$
,
![]() $a=2$
, (c) one sinusoidal phase modulation with
$a=2$
, (c) one sinusoidal phase modulation with
![]() $\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}+\unicode[STIX]{x1D70B}/3$
,
$\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}+\unicode[STIX]{x1D70B}/3$
,
![]() $a=3.5$
and (e) two sinusoidal phase modulations with
$a=3.5$
and (e) two sinusoidal phase modulations with
![]() $\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}+\unicode[STIX]{x1D70B}/3$
,
$\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}+\unicode[STIX]{x1D70B}/3$
,
![]() $a_{1}=3$
,
$a_{1}=3$
,
![]() $a_{2}=2$
. The corresponding temporal ripples are shown in (b), (d) and (f) and the intensity scale is normalized to mean intensity.
$a_{2}=2$
. The corresponding temporal ripples are shown in (b), (d) and (f) and the intensity scale is normalized to mean intensity.

Figure 3. Schematic representations of the focusing process for an SSD beam (single sinusoidal phase modulation). Integration of intensity on focal plane can reduce the distortion criterion of SSD beam. The colors represent the isointensity surface in near field, and the horizontal dashed line corresponds to AM patterns in near field as shown in Figure 2.
When multi-plates are applied in series in system, ignoring the high order of AM terms, the temporal intensity is calculated as
 $$\begin{eqnarray}\displaystyle I(t,x) & = & \displaystyle \mathop{\prod }_{i=1}^{N}I_{i}(t,x)=\mathop{\prod }_{i=1}^{N}(1-R)^{2}\left|A_{0}\left(t-\frac{nd}{c}\right)\right|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{i=1}^{N}[1+2R\unicode[STIX]{x1D702}\cos \unicode[STIX]{x1D6F7}(t,x)]\nonumber\\ \displaystyle & {\approx} & \displaystyle \left\{1+2\mathop{\sum }_{i=1}^{N}[R_{i}\unicode[STIX]{x1D702}_{i}\cos \unicode[STIX]{x1D6F7}_{i}(t,x)]\right\}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{i=1}^{N}(1-R_{i})^{2}\left|A_{0}\left(t-\frac{nd_{i}}{c}\right)\right|^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(t,x) & = & \displaystyle \mathop{\prod }_{i=1}^{N}I_{i}(t,x)=\mathop{\prod }_{i=1}^{N}(1-R)^{2}\left|A_{0}\left(t-\frac{nd}{c}\right)\right|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{i=1}^{N}[1+2R\unicode[STIX]{x1D702}\cos \unicode[STIX]{x1D6F7}(t,x)]\nonumber\\ \displaystyle & {\approx} & \displaystyle \left\{1+2\mathop{\sum }_{i=1}^{N}[R_{i}\unicode[STIX]{x1D702}_{i}\cos \unicode[STIX]{x1D6F7}_{i}(t,x)]\right\}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{i=1}^{N}(1-R_{i})^{2}\left|A_{0}\left(t-\frac{nd_{i}}{c}\right)\right|^{2}.\end{eqnarray}$$
Equation (14) indicates that AM with multi-plates has similar patterns and increased distortion criterion compared to the one plate scenario. When multi-plates have equal thickness (in high-power laser facility, only the beam passing through one plate by multi-times can satisfy this condition), the distortion criterion is superposed with linearity as
![]() $\unicode[STIX]{x1D6FC}=4\sum _{i=1}^{N}R_{i}\unicode[STIX]{x1D702}_{i}$
. Otherwise, the distortion criterion is superposed with quadratic sum as
$\unicode[STIX]{x1D6FC}=4\sum _{i=1}^{N}R_{i}\unicode[STIX]{x1D702}_{i}$
. Otherwise, the distortion criterion is superposed with quadratic sum as
![]() $\unicode[STIX]{x1D6FC}=4\sqrt{\sum _{i=1}^{N}(R_{i}\unicode[STIX]{x1D702}_{i})^{2}}$
because of the random equivalent phase
$\unicode[STIX]{x1D6FC}=4\sqrt{\sum _{i=1}^{N}(R_{i}\unicode[STIX]{x1D702}_{i})^{2}}$
because of the random equivalent phase
![]() $\unicode[STIX]{x1D6F7}_{i}(t,x)$
. Supposing
$\unicode[STIX]{x1D6F7}_{i}(t,x)$
. Supposing
![]() $n_{i}$
is the passing number for the
$n_{i}$
is the passing number for the
![]() $i$
th plate, the integral distortion criterion of multi-plates can be obtained as
$i$
th plate, the integral distortion criterion of multi-plates can be obtained as
![]() $\unicode[STIX]{x1D6FC}=4\sqrt{\sum _{i=1}^{N}(n_{i}R_{i}\unicode[STIX]{x1D702}_{i})^{2}}$
.
$\unicode[STIX]{x1D6FC}=4\sqrt{\sum _{i=1}^{N}(n_{i}R_{i}\unicode[STIX]{x1D702}_{i})^{2}}$
.
4 AM of SSD beam induced by etalon effect in far field
For an SSD beam expressed as Equation (10),
![]() $kx$
is the phase factor associated with space, which represents that the grating generates a time delay proportional to
$kx$
is the phase factor associated with space, which represents that the grating generates a time delay proportional to
![]() $x$
. In the focusing process, the lens simply acts as an integrator on the focal plane, as presented in Figure 3. Therefore, the far-field intensity is temporally averaged due to the time delay.
$x$
. In the focusing process, the lens simply acts as an integrator on the focal plane, as presented in Figure 3. Therefore, the far-field intensity is temporally averaged due to the time delay.
For a spatially flat-top beam, the far-field intensity is linked to near-field intensity by the following expression:
 $$\begin{eqnarray}\displaystyle I_{f\!\!f}(t) & = & \displaystyle \int _{-D/2}^{D/2}I_{0}(t,x)\,\text{d}x=\int _{-D/2}^{D/2}(1-R)^{2}\nonumber\\ \displaystyle & & \displaystyle \times \left|A_{0}\left(t-\frac{nd}{c}\right)\right|^{2}\left\{\vphantom{\frac{2nd}{c}}1+2R\unicode[STIX]{x1D702}\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.\cos \left\{a\cos \left[\unicode[STIX]{x1D714}\left(t-\frac{2nd}{c}\right)+kx\right]+\unicode[STIX]{x1D711}_{0}\right\}\right\}\text{d}x\nonumber\\ \displaystyle & = & \displaystyle (1-R)^{2}\left|A_{0}\left(t-\frac{nd}{c}\right)\right|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \left\{\vphantom{\int _{-D/2}^{D/2}}D+2R\unicode[STIX]{x1D702}\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.\int _{-D/2}^{D/2}\cos \left\{a\cos \left[kx+\unicode[STIX]{x1D714}\left(t-\frac{2nd}{c}\right)\right]\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.\vphantom{\int _{-D/2}^{D/2}}+\unicode[STIX]{x1D711}_{0}\right\}\text{d}x\right\}=I_{M}(t)+I_{AM}(t),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{f\!\!f}(t) & = & \displaystyle \int _{-D/2}^{D/2}I_{0}(t,x)\,\text{d}x=\int _{-D/2}^{D/2}(1-R)^{2}\nonumber\\ \displaystyle & & \displaystyle \times \left|A_{0}\left(t-\frac{nd}{c}\right)\right|^{2}\left\{\vphantom{\frac{2nd}{c}}1+2R\unicode[STIX]{x1D702}\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.\cos \left\{a\cos \left[\unicode[STIX]{x1D714}\left(t-\frac{2nd}{c}\right)+kx\right]+\unicode[STIX]{x1D711}_{0}\right\}\right\}\text{d}x\nonumber\\ \displaystyle & = & \displaystyle (1-R)^{2}\left|A_{0}\left(t-\frac{nd}{c}\right)\right|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \left\{\vphantom{\int _{-D/2}^{D/2}}D+2R\unicode[STIX]{x1D702}\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.\int _{-D/2}^{D/2}\cos \left\{a\cos \left[kx+\unicode[STIX]{x1D714}\left(t-\frac{2nd}{c}\right)\right]\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.\vphantom{\int _{-D/2}^{D/2}}+\unicode[STIX]{x1D711}_{0}\right\}\text{d}x\right\}=I_{M}(t)+I_{AM}(t),\end{eqnarray}$$
where
![]() $I_{M}(t)$
and
$I_{M}(t)$
and
![]() $I_{AM}(t)$
are the mean intensity and modulation intensity, respectively. The relative modulation
$I_{AM}(t)$
are the mean intensity and modulation intensity, respectively. The relative modulation
![]() $I_{AM}(t)/I_{M}(t)$
is calculated as
$I_{AM}(t)/I_{M}(t)$
is calculated as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{I_{AM}(t)}{I_{M}(t)}=2R\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{-1/2}^{1/2}\cos \!\left\{a\cos \!\left[2\unicode[STIX]{x1D70B}N_{c}x_{0}+\unicode[STIX]{x1D714}\left(t-\frac{2nd}{c}\right)\right]\!+\unicode[STIX]{x1D711}_{0}\right\}\text{d}x_{0}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{I_{AM}(t)}{I_{M}(t)}=2R\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{-1/2}^{1/2}\cos \!\left\{a\cos \!\left[2\unicode[STIX]{x1D70B}N_{c}x_{0}+\unicode[STIX]{x1D714}\left(t-\frac{2nd}{c}\right)\right]\!+\unicode[STIX]{x1D711}_{0}\right\}\text{d}x_{0}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

Figure 4. (a) Dependence of the far-field distortion criterion on the number of color cycle for an SSD beam, where the equivalent phase of
![]() $\unicode[STIX]{x1D711}_{0}$
is 0,
$\unicode[STIX]{x1D711}_{0}$
is 0,
![]() $\unicode[STIX]{x1D70B}/6$
,
$\unicode[STIX]{x1D70B}/6$
,
![]() $\unicode[STIX]{x1D70B}/3$
and
$\unicode[STIX]{x1D70B}/3$
and
![]() $\unicode[STIX]{x1D70B}/2$
, respectively. (b) The comparison of AM patterns in near field and far field for an SSD beam with the parameters
$\unicode[STIX]{x1D70B}/2$
, respectively. (b) The comparison of AM patterns in near field and far field for an SSD beam with the parameters
![]() $N_{c}=1.3$
and
$N_{c}=1.3$
and
![]() $\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}+\unicode[STIX]{x1D70B}/3$
.
$\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}+\unicode[STIX]{x1D70B}/3$
.
Here the transform
![]() $x_{0}=x/D$
is applied. From Equation (16) it can be indicated that, AM in the far field has similar patterns and reduced distortion criterion to the near field. Equation (16) clearly shows the dependence of distortion criterion on the number of color cycle. When
$x_{0}=x/D$
is applied. From Equation (16) it can be indicated that, AM in the far field has similar patterns and reduced distortion criterion to the near field. Equation (16) clearly shows the dependence of distortion criterion on the number of color cycle. When
![]() $N_{c}\rightarrow 0$
, the distortion criterion of the far field has the maximum value
$N_{c}\rightarrow 0$
, the distortion criterion of the far field has the maximum value
![]() $\unicode[STIX]{x1D6FC}=4R\unicode[STIX]{x1D702}$
, which is the same as the near field. When
$\unicode[STIX]{x1D6FC}=4R\unicode[STIX]{x1D702}$
, which is the same as the near field. When
![]() $N_{c}$
is an integer, the distortion criterion becomes 0 at any time slice, and AM on the far field disappears. Generally, the distortion criterion has a decreasing trend with
$N_{c}$
is an integer, the distortion criterion becomes 0 at any time slice, and AM on the far field disappears. Generally, the distortion criterion has a decreasing trend with
![]() $N_{c}$
increasing, and the constant phase
$N_{c}$
increasing, and the constant phase
![]() $\unicode[STIX]{x1D711}_{0}$
has an influence on the distortion criterion especially when
$\unicode[STIX]{x1D711}_{0}$
has an influence on the distortion criterion especially when
![]() $N_{c}$
is small.
$N_{c}$
is small.
We then investigate the number of color cycle dependence of the distortion criterion by numerical illustrations as follows. During the calculation, the temporal pulse profile was flat-in-time and 3 ns wide, SSD parameters are the same as in Figure 2(c) and the distortion criterion induced by the etalon effect is
![]() $\unicode[STIX]{x1D6FC}=20\%$
in the near field. The distortion criterion trend is shown in Figure 4(a). It shows that with increasing
$\unicode[STIX]{x1D6FC}=20\%$
in the near field. The distortion criterion trend is shown in Figure 4(a). It shows that with increasing
![]() $N_{c}$
, the distortion criterion in far field decreases integrally and it has an inflection point at the position where
$N_{c}$
, the distortion criterion in far field decreases integrally and it has an inflection point at the position where
![]() $N_{c}$
is an integer; the constant phase
$N_{c}$
is an integer; the constant phase
![]() $\unicode[STIX]{x1D711}_{0}$
does not change the characteristic of the curve but can modify the details. For clear comparisons, in Figure 4(b), we give an example of AM patterns in the near field and the far field, and the corresponding parameters are
$\unicode[STIX]{x1D711}_{0}$
does not change the characteristic of the curve but can modify the details. For clear comparisons, in Figure 4(b), we give an example of AM patterns in the near field and the far field, and the corresponding parameters are
![]() $N_{c}=1.3$
and
$N_{c}=1.3$
and
![]() $\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}+\unicode[STIX]{x1D70B}/3$
, respectively. We can see that AM in the far field and near field has similar patterns, but the distortion criterion in the far field is obviously smaller. The analytical results are in good agreement with the simulation ones.
$\unicode[STIX]{x1D711}_{0}=2\unicode[STIX]{x1D70B}n_{0}+\unicode[STIX]{x1D70B}/3$
, respectively. We can see that AM in the far field and near field has similar patterns, but the distortion criterion in the far field is obviously smaller. The analytical results are in good agreement with the simulation ones.
5 Conclusion
Etalon effect is a factor that would cause the spectral transmission distortion and hence impose the FM-to-AM conversion in high-power laser system. SSD beam is a very special broadband beam for its monochromatic feature at the given time and space in near field. The traditional method which uses the optical spectral transfer function as filters cannot accurately describe its AM characteristics. Based on the beam mixing process in the transmission optics, the theories of etalon effect for SSD shaped pulse are studied. With a low-order approximation, the analytic model of temporal shape of SSD beam is achieved for the first time. It concludes that the distortion criterion is proportional to the residual reflectivity of the plate and the temporal gradient of the pulse. Since AM patterns contain many ripples with different amplitudes and widths, a precisely designed plate thickness can reduce the ripples’ number and amplitude. Additionally, multiple elements in series are analyzed; it indicates that multiple phase modulations in series would increase the complexity of the patterns, and multi-plates in series would increase the distortion criterion. Finally, the FM-to-AM conversion on focal plane is investigated; the integration of intensity on focal plane can reduce AM of SSD beam impacted by the etalon effect and the distortion criterion is reduced by increasing the number of the color cycle. Because AM control is necessary for the near field to avoid optics damage and for the far field to ensure an optimal interaction of laser–target, our investigations could provide some important phenomena and rules for pulse shape control.
Acknowledgements
The reported investigations were supported by the National Natural Science Foundation of China (No. 11404306) and the Presidential Foundation of the China Academy of Engineering Physics (No. YZJJLX2016008).