Acceleration of 60 MeV proton beams in the commissioning experiment of the SULF-10 PW laser

Abstract

We report the experimental results of the commissioning phase in the 10 PW laser beamline of the Shanghai Superintense Ultrafast Laser Facility (SULF). The peak power reaches 2.4 PW on target without the last amplifying during the experiment. The laser energy of 72 ± 9 J is directed to a focal spot of approximately 6 μm diameter (full width at half maximum) in 30 fs pulse duration, yielding a focused peak intensity around 2.0 × 10²¹ W/cm². The first laser-proton acceleration experiment is performed using plain copper and plastic targets. High-energy proton beams with maximum cut-off energy up to 62.5 MeV are achieved using copper foils at the optimum target thickness of 4 μm via target normal sheath acceleration. For plastic targets of tens of nanometers thick, the proton cut-off energy is approximately 20 MeV, showing ring-like or filamented density distributions. These experimental results reflect the capabilities of the SULF-10 PW beamline, for example, both ultrahigh intensity and relatively good beam contrast. Further optimization for these key parameters is underway, where peak laser intensities of 10²²–10²³ W/cm² are anticipated to support various experiments on extreme field physics.

1 Introduction

Chirped-pulse amplification (CPA) technology has significantly advanced the development of ultrashort ultraintense lasers in the past few decades^{[ 1– 3]}. Today, nearly one hundred 100 TW systems are operating, with about 20 systems at the PW level existing or under construction^{[ 3]}, pushing laser intensities to go beyond the relativistic threshold (about 10¹⁸ W/cm² for laser wavelengths of ~μm). Unprecedented extreme physical conditions can be created in laboratories^{[ 4– 6]}, which strongly motivate the studies of laser-driven particle acceleration^{[ 4, 7, 8]}, X/gamma ray radiation^{[ 9– 11]}, laboratory astrophysics^{[ 6, 12, 13]}, laser-driven nuclear physics^{[ 14]}, etc. On the other hand, the rising interest in strong-field quantum electrodynamics calls for lasers with even higher intensities (10²²–10²³ W/cm²). Such a quest has been supported by several projects aiming to reach 10 PW-level outputs, such as ELI^{[ 15]}, Vulcan-10 PW^{[ 16]}, Apollon-10 PW^{[ 17]} and SULF-10 PW^{[ 18]}. The first 100 PW-level laser facility under construction is the Station of Extreme Light Science (SEL)^{[ 19]}, while several others are also under consideration (ELI-200 PW, XCELS, Nexawatt, Gekko EXA, Rochester, etc.).

The Shanghai Superintense Ultrafast Laser Facility (SULF) is the first 10 PW-class laser facility in China, which was proposed and constructed by the Shanghai Institute of Optics and Fine Mechanics (SIOM) in July 2016. Figure 1 shows the layout of the SULF laser facility^{[ 20]}. The SULF laser employs a typical CPA Ti:sapphire scheme and contains two high-intensity laser beamlines, SULF-10 PW, operating at a repetition rate of one shot per 3 minutes^{[ 21]}, and SULF-1 PW, operating at a repetition rate of 0.1 Hz^{[ 22]}. In 2018, the SULF-10 PW beamline realized output peak power up to 10.3 PW (after compression) with 339 J output pulse energy (compressor transmission efficiency of 64%) compressed to 21 fs pulse duration^{[ 18]}. This peak power was further increased to 12.9 PW in 2019^{[ 21]}. The physical experimental areas in SULF include the three research platforms of dynamics of materials under extreme conditions (DMEC), ultrafast sub-atomic physics (USAP) and big molecule dynamics and extreme-fast chemistry (MODEC).

Figure 1 The layout of the SULF laser facility^{[ 20]}.

The commissioning experiment of the SULF-10 PW beamline was carried out on the USAP platform, focusing on laser-proton acceleration using plain Cu and plastic targets. The peak power reaches 2.4 PW without the last amplifying section, corresponding to laser energy of 72 ± 9 J, focal spot size of approximately 6 μm diameter (full width at half maximum (FWHM)) and 30 fs pulse duration. These together yield a focused peak intensity around 2.0 × 10²¹ W/cm². We obtained a proton beam with cut-off energy up to 62.5 MeV using the Cu target at the optimum target thickness of 4 μm. For much thinner targets (tens of nanometers), the proton cut-off energy declines to 20 MeV and ring-like or filamented structures appear in the density distribution. The obtained results from laser–foil interaction directly illustrate the current capabilities of the SULF-10 PW beamline.

2 The current status of the experimental area and SULF-10 PW beamline

2.1 Experimental area in USAP

As seen in Figure 1, the SULF-10 PW laser beam goes through seven multi-pass amplifiers on the first floor of the SULF building, and then is transmitted to floor B2 through a transmission pipeline. Following that, the amplified beam is further expanded and the image is relayed into the compressor cavity. Behind the compressor chamber are the beam-quality improvement chamber and experimental chamber (USAP). Figure 2 shows a photograph of the experimental area in USAP located on floor B2. The beam-quality improvement chamber is specially designed to place a deformable mirror (DM) and plasma mirrors (PMs) to further improve the beam quality and contrast of the laser. The experimental chamber for laser–matter interaction comprises two vacuum cavities, the larger one for short-focal-length experiments, such as laser-ion acceleration, and the smaller one for experiments requiring a long focal length, such as laser wakefield acceleration of electrons. The internal size of both the beam-quality improvement and the short-focal-length chambers is 4.5 m × 3.5 m × 2.0 m and it takes about 1 hour for the vacuum system to pump it from standard atmospheric pressure down to 10^–4–10^–3 Pa. An important function of the USAP platform is that it allows users to simultaneously employ both the SULF-10 PW and SULF-1 PW beamlines, for either pump-probe or laser-electron scattering experiments. In the commissioning experiment on the SULF-10 PW beamline, only the off-axis parabola (OAP) of short focal length and the DM in the beam-quality improvement chamber were employed without introducing the PMs in the laser path.

Figure 2 The experimental area in USAP.

2.2 Laser parameters of the SULF-10 PW beamline

In the commissioning stage, the output energy of the SULF-10 PW laser before the compressor is measured to be 110 ± 13 J with six multi-pass amplifiers (the last one was switched off). The energy transmission efficiency from the compressor to the target is 66%, resulting in the on-target energy of 72 ± 9 J. The near-field profile of the final output laser is elliptic, 470 mm × 430 mm along the horizontal and vertical directions, respectively. The measured modulation of the near-field beam is about 1.8, mainly due to the modulation of the pump laser beam from the main amplifier.

Decreasing the size of the focal spot is an efficient method to increase the laser intensity. However, the large-aperture optic elements implemented in the SULF-10 PW system inevitably increase the wavefront aberrations. Here, double DMs with different actuator densities are cascaded to optimize the wavefront aberrations and, hence, the focal intensity^{[ 23]}. The first adaptive-optics (AO) correction system is placed at the output of the sixth amplifier, and the DM has a diameter of 130 mm with 64 mechanical actuators. A second AO correction loop is installed using a larger DM with 520 mm diameter and 121 mechanical actuators. It is placed at the output of compressor (in the beam-quality improvement chamber). The wavefront sampling laser is exported out of the experimental chamber following the light path built after an OAP. The focal spot is amplified by 10 times and then online monitored by a low-noise charge-coupled device (CCD). An OAP with 2000 mm focal length is used for laser-proton acceleration, corresponding to an effective f-number of 4.4. Figure 3(a) shows the typical focal laser intensity distribution after the correction. The FWHM size of focal spot is 6.28 μm × 5.92 μm, containing 24% of the total laser energy.

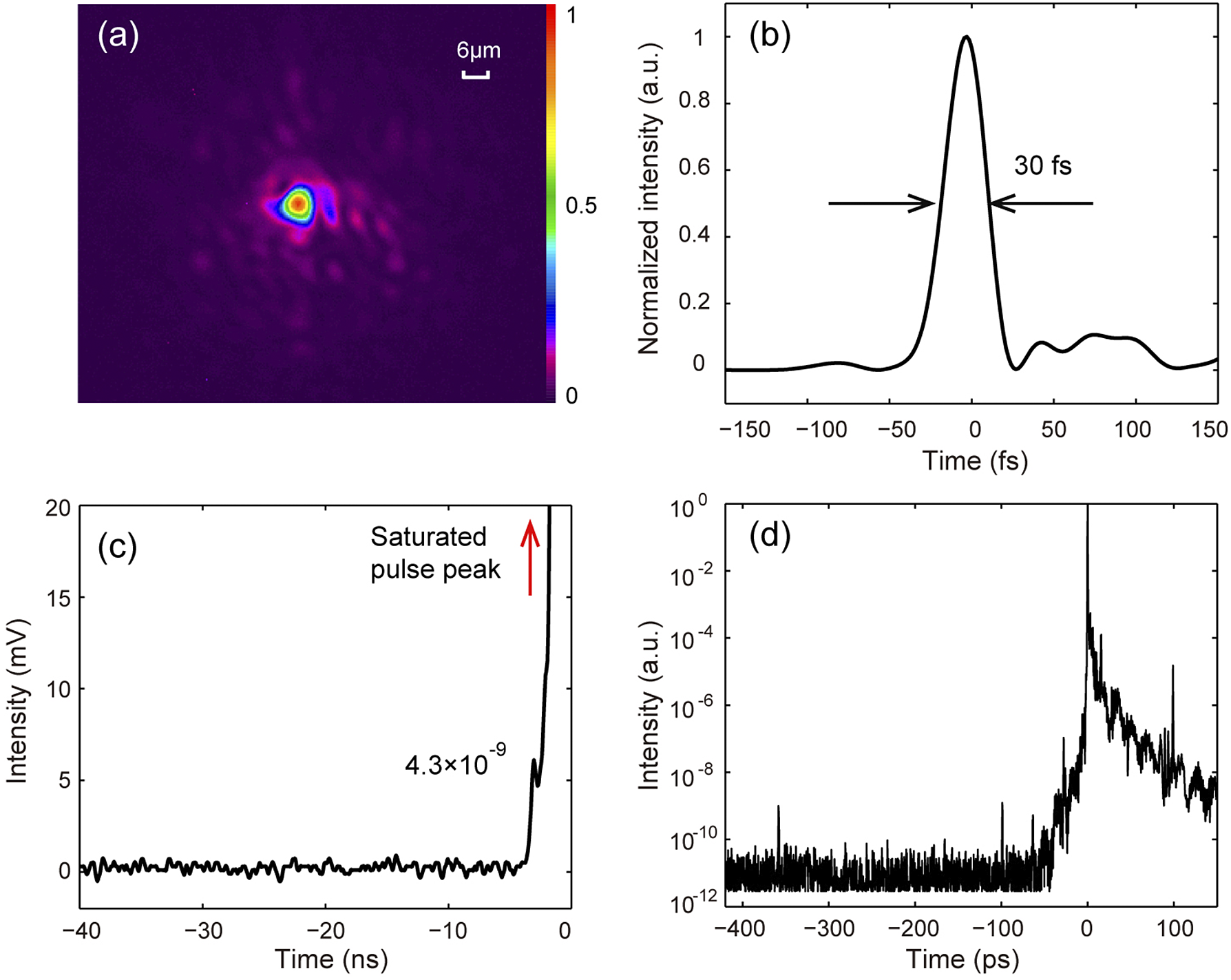
Figure 3 Laser parameters of the SULF-10 PW beamline for the commissioning experiment. (a) The typical focal spot of the laser after the correction of the double DM system, which is measured using a low-noise CCD by the light path built after an f/4.4 OAP. (b) The typical pulse duration of the compressed pulse measured by a Fastlite Wizzler instrument. The temporal contrast of (c) the nanosecond scale measured by a photodiode with a stack of neutral attenuators and (d) the picosecond scale measured by a third-order cross-correlator. The red arrow represents the saturated peak of the laser pulse.

The measured spectral width of the output pulse is ±40 nm (FWHM) at 800 nm central wavelength. The laser beam is compressed by a four-grating compressor and the pulse duration is measured using a Fastlite Wizzler instrument. Figure 3(b) shows that the typical pulse duration is about 30 fs (FWHM), resulting in an output peak power of 2.4 PW. These data indicate that the focal peak intensity reaches 2.0 × 10²¹ W/cm².

A key parameter for laser–solid interaction at relativistic intensities is the temporal contrast of the laser pulse. Pre-pulses of intensity above 10¹⁰ W/cm^{2[ 24]} would ionize the target, introducing low-density pre-plasmas in front of the target, which could enhance proton acceleration^{[ 25, 26]}. However, if the pre-plasma induced by pre-pulse driven shock appears at the target rear, proton acceleration will be restricted^{[ 27]}. In order to improve the temporal contrast of the SULF-10 PW beamline, a combination of cross-polarized wave generation (XPWG) and femtosecond optical parametric amplification (OPA) techniques is implemented at the front end^{[ 28]}. Along with further optimization^{[ 29]}, the contrast ratio at 50 ps before the main pulse is measured to be around 1.7 × 10^–9. Meanwhile, two Pockels cells are installed after the first amplifier to increase the nanosecond temporal contrast. Here, the contrast evolution at the nanosecond scale was measured by a combination of an oscilloscope and a photodiode at the output of the compressor, as shown in Figure 3(c). It can be found that the amplified spontaneous emission (ASE) noise level is better than 10^–9 (limited by the photodiode). An intense pre-pulse is also seen at –3 ns with the contrast of approximately 4.3 × 10^–9, for reasons that are still under investigation. The temporal contrast at the picosecond scale was measured by a commercial third-order cross-correlator (Amplitude, Sequoia). The contrast curve within –420 ps before the main pulse is illustrated in Figure 3(d), showing a pedestal around 10^–11, which starts rising from –50 ps. In addition, three pre-pulses appear at –360, –100 and –60 ps with the contrast ratio of approximately 10^–9 due to multiple reflections of the optical components in the amplifiers (the detailed analysis of pre-pulses will be introduced in another paper). Considering the laser intensity of 10²¹ W/cm², these pre-pulses reach intensities of 10¹² W/cm², sufficiently strong to trigger material ionization, and could induce pre-plasmas on the target rear. PMs are to be installed in the near future to improve the performance on laser–foil interactions.

3 Experimental results

3.1 Experimental setup

A sketch of the experimental setup is shown in Figure 4. The p-polarized laser pulse is focused by the f/4.4 OAP mirror onto the target at an incident angle of 15^°. In this run, the target table accommodates seven planar foils (could be more if necessary). The specially designed stacks of radiochromic films (RCFs) and BAS-SR image plates (IPs), located 6.3 cm behind the rear of the target, are used to measure the profile and energy spectrum of protons and electrons, respectively. These stacks are of 50 mm × 50 mm, with a 3-mm-diameter hole in the center to let protons pass through, and enwrapped by 15 μm-thickness Al foil to shield debris. Copper and aluminum sheets of different thickness are inserted between the RCFs and SR-IPs to attenuate proton and electron energy, respectively. Due to limited space, only two stacks are used simultaneously in an experiment.

Figure 4 The sketch of the experimental setup. The specially designed stacks of radiochromic films and BAS-SR image plates are used to measure the profile and energy spectrum of protons and electrons. The stacks and targets can move along the y direction. Two Thomson parabola spectrometers are used to detect the ion spectra at the target normal direction and laser direction. It installs six BAS-TR image plates at a time.

Two types of Thomson parabola (TP) spectrometers (TP1 and TP2) are used to detect the proton energy spectrum, as shown in Figure 4. TP1, composed of a 1.0 T magnetic field over 5-cm length and a pair of 15-cm long copper electrodes charged up to 10 kV, is placed 87.8 cm away from the target along the target normal direction. The diameter of TP1’s pinhole is 150 μm, corresponding to the solid angle of 2.3 × 10^–8 sr. The energy resolution of TP1 is 0.4 MeV at 100 MeV, with a low energy threshold of 3.5 MeV. The other high-resolution TP spectrometer, TP2, placed 80 cm away from the target along the laser direction, is switched on when the RCFs and IPs are not in use. TP2 employs a magnetic field of 1.7 T over 5-cm length and electrodes up to 35 cm length with 10 kV. It has a pinhole of 200 μm diameter, corresponding to a 4.9 × 10^–8 sr solid angle. The energy resolution reaches 0.13 MeV at 100 MeV and the lower energy threshold is 9.2 MeV. From Figure 4, one should note that the ions cannot be detected by TP2 if the stacks move in. In both TPs, BAS-TR IPs are placed at a turntable holder that can rotate 360° in the horizontal plane, allowing for six successive measurements without interruption. Both of the TPs are surrounded by a lead shield to reduce the signal noise during experiments. For future development, an online detector, named a microchannel plate (MCP), with a fluorescent screen^{[ 30]} will be installed to improve the diagnosis efficiency.

3.2 Acceleration of a 60 MeV proton beam via target normal sheath acceleration

The maximum energy of protons accelerated by intense ultrafast lasers is mainly determined by, but not limited to, the laser intensity, pulse duration and pulse contrast ratio, and thus is considered as an important perspective to find out a laser facility’s capabilities. The most widely studied mechanisms for laser-driven ion acceleration are target normal sheath acceleration (TNSA)^{[ 31, 32]} and radiation pressure acceleration (RPA)^{[ 33, 34]}, which require different laser and target parameters. In the commissioning experiment, under the current conditions of the SULF-10 PW described above, we focus on TNSA using micrometer-thick Cu foils.

The proton cut-off energy as a function of target thickness is shown in Figure 5(a), measured by TP1 along the target normal direction and by both TP2 and RCF stacks along the laser propagation direction. The target thickness l of the Cu foil varies from 1 to 10 μm. It can be clearly seen that in both directions, the proton cut-off energy increases when the foil thickness increases from 1 to 4 μm, and then decreases with larger thickness, corresponding to an optimum value at 4 μm. This trend agrees with the previously reported results for TNSA-produced proton beams, where the effects of electron reflux and pre-pulse-induced plasma expansion at the target rear side result in an optimum target thickness for proton acceleration^{[ 35]}. One notices that the proton energies along the target normal direction are much higher than those along the laser direction for all target thicknesses. Typical proton spectra for various target thicknesses are illustrated in Figure 5(b), showing the broad-energy-spread distribution.

Figure 5 (a) The proton cut-off energy as a function of the target thickness of the plain Cu foils measured by TP1 in the target normal direction (red squares) and by both TP2 and RCF stacks in the laser propagation direction (blue circles), where the red and blue lines represent the average proton energy over two to three shots. The vertical error bars for some data are defined by the energy interval between adjacent RCF layers. (b) Typical proton spectra for five target thicknesses of l = 1 μm (black line), 2 μm (blue line), 4 μm (red line), 7 μm (magenta line) and 10 μm (cyan line) in the target normal direction, respectively. The proton energy spectrum for l = 4 μm (dashed red line) in the laser direction is also included in (b). (c), (d) The raw IP data of TP1 and TP2 for the best result of proton acceleration from a shot on a 4-μm Cu foil, where the inset in (c) is a magnified image of the ion trace in the high-energy region.

For 4-μm-thick foils, the average cut-off energy of protons is 60 MeV according to the data from three shots, where the highest one achieves 62.5 MeV. This is among the state-of-the-art results in proton acceleration using femtosecond lasers according to previous reports^{[ 31, 36]}. Figures 5(c) and 5(d) show the raw IP data of TP1 and TP2 for the best case with the 4-μm Cu target, from which the proton energy spectra are extracted and presented in Figure 5(b). Note that both the cut-off energy and particle number of protons in the target normal direction are much higher than those measured along the laser propagation direction. The cut-off energies are 42.5 MeV (laser direction) and 62.5 MeV (target normal direction), respectively. From the proton spectrum of the best shot (see in Figure 5(b)), the proton number for energy of more than 3.5 MeV can be estimated and reaches up to 2.4 × 10¹², corresponding to a 1.5% energy conversion efficiency (assuming the proton beam has a divergence half-angle of 10°).

Typical proton profiles from three shots on Cu targets of l = 1, 4 and 10 μm are shown in Figure 6(a) at selected layers of RCF stacks, with the highest energy detected of 44.3, 52.1 and 32.2 MeV, respectively. These results are slightly lower than the actual values according to the signal of TP1 with the cut-off energies of 47.3, 58.9 and 36.3 MeV for the same shots. This is mainly due to not only the large interval of energy measurement between adjacent RCF layers but also the use of the HD-V2 type RCFs, which cannot detect the low-density protons in the high-energy region. It can be found from Figure 6(a) that the proton signal monotonically decreases at higher energies. Figure 6(b) shows the corresponding divergent angle of the proton beam as a function of the energy. Protons are more collimated at higher energies. The minimum divergences measured for l = 1, 4 and 10 μm are 8.4°, 7.6° and 12.5°, respectively. It is a typical feature in the TNSA regime, which is different from that of RPA-produced protons where the beam is more divergent at higher proton energies^{[ 37, 38]}. From the density profiles of protons more than 32.2 MeV, it can be found that the center of the proton beams is not exactly aligned with the target normal direction, but shifts slightly toward the laser direction in the cases of l = 1 and 4 μm (see Figure 6(a)). This is mainly due to the bending of the target surface induced by the laser pre-pulse before the main pulse arrives^{[ 39]}.

Figure 6 (a) Typical proton profiles from three shots on Cu targets of l = 1, 4 and 10 μm at selected layers of RCF stacks corresponding to the proton energies of 11.6, 23.8, 32.2, 44.3 and 52.1 MeV, respectively. The target normal direction (0°) and laser direction (15°) are illustrated by dashed blue and red lines for 11.6 and 32.2 MeV. (b) Divergent angles of protons at different energies for l = 1 μm (blue circles), 4 μm (red squares) and 10 μm (black triangles).

The electron number distributions are also measured using IP stacks that record electrons of energy over 11.8, 14.2, 17.2, 20.2 and 23.7 MeV (electrons with energies lower than 11 MeV are stopped by the RCF stacks), respectively. As shown in Figure 7(a), the emitting direction of the electrons also shifts slightly toward the laser direction (>0°), similar to the proton beam (see in Figure 6(a)). Considering the total electron signal within each IP shown in Figure 7(a), the electron numbers within four energy intervals of 11.8–14.2, 14.2–17.2, 17.2–20.2 and 20.2–23.7 MeV are obtained and the processed spectrum is displayed in Figure 7(b). The fitting curve of the electron spectrum indicates an electron temperature T _e of 7.6 MeV, which agrees reasonably well with the theoretical result of 8.6 MeV following the ponderomotive scaling law given by ${T}_{\mathrm{e}}\left({m}_{\mathrm{e}}{c}^2\right)={\int}_0^{\frac{2\pi}{{\mathrm{w}}_0}}\sqrt{1+{a}_0^2{\sin}^2\left({w}_0t\right)} \mathrm{d}t/\left(2\pi /{w}_0\right)\hbox{--} 1$ ^{[ 40]}, where ${m}_e$ , $c$ , ${a}_0$ and ${w}_0$ are the electron mass, light speed, peak normalized vector potential and angular frequency of the laser pulse, respectively (the laser intensity for this shot is 1.7 × 10²¹ W/cm²). The features mentioned above suggest that TNSA is dominant, given the provided laser intensity and micrometer-thick Cu foils. Both the 60 MeV proton beams of several shots and the electron temperature reflect the current capabilities of the SULF-10 PW beamline for providing laser beams with ultrahigh intensity, ultrashort duration and relatively high contrast.

Figure 7 (a) Electron number distribution measured using IP stacks for electron energies greater than 11.8, 14.2, 17.2, 20.2 and 23.7 MeV, from the same shot on a 4-μm-thick Cu target, as illustrated in Figure 6. (b) The processed electron spectrum, where the dashed line represents the fitting curve.

3.3 Proton acceleration using nanometer-thick targets

Laser-driven proton acceleration using nanometer-thick plastic (CH) foils is also investigated here. The profiles of proton beams at selected energies for CH foils with target thicknesses of l = 30, 40 and 70 nm are exhibited in Figure 8. The highest proton energies shown by the RCF are smaller than those measured by TP1 with the cut-off energies of 19.2, 20.0 and 19.4 MeV for l = 30, 40 and 70 nm, respectively. Clear ring-like profiles appear for l = 30 and 40 nm on all RCF layers, which is probably induced by the relativistic transparency effect in nanometer target situation^{[ 37]}. In both cases, the divergent angles of protons remain almost unchanged at different energies and the center of the proton beams is well aligned along the target normal direction, as shown in Figures 8(a) and 8(b), in contrast to the TNSA case using micrometer-thick targets^{[ 39]} and the RPA case^{[ 37]}. Such properties indicate that protons are not effectively accelerated since ionization and pre-expanding of nanometer-thick targets driven by pre-pulses may lead to relativistically transparent plasma^{[ 41]}.

Figure 8 Proton beam profiles for plain CH targets with three different thicknesses of (a1)–(a4) 30 nm, (b1)–(b4) 40 nm and (c1)–(c4) 70 nm, at selected proton energies of 4.8, 7.2, 11.6 and 15.9 MeV, respectively. The dashed lines in blue and red represent the target normal direction (0°) and laser direction (15°), respectively.

A filamented structure emerges when the target thickness increases to 70 nm (see Figures 8(c1)–8(c4)), which is possibly associated with Weibel instability^{[ 42]} or the wrinkles on the target surface^{[ 43]}. The divergent angles of protons become smaller for more energetic protons, while the center of the proton beam profile mainly concentrates near the laser propagation axis. It is an obvious sign that the plasma is still opaque rather than transparent. Considering the use of linearly polarized lasers and an oblique incidence angle of 15°, the proton acceleration for the l = 70 nm case may be dominant by using a hybrid scheme where both the hole boring stage^{[ 44]} of RPA and TNSA play important roles. The results with nanometer-thick targets show that the laser contrast of the SULF-10 PW beamline is not sufficient to drive effective acceleration schemes, such as RPA^{[ 33, 34]} and acceleration using a structural target^{[ 45, 46]}. Proton energies beyond 100 MeV are expected after further optimization of the temporal contrast and focal spot of the SULF-10 PW beamline.

4 Conclusions and perspectives

A commissioning experiment of the SULF-10 PW beamline has been carried out, focusing on laser-proton acceleration with plain Cu and plastic targets. The SULF-10 PW laser beamline can provide 2.4 PW peak power on target currently. A high-energy proton beam with maximum cut-off energy up to 62.5 MeV was achieved with Cu foils at the optimum target thickness of 4 μm via TNSA, which is approaching the requirement of tumor therapy treatment^{[ 47]}. For plastic targets of tens-of-nanometer thickness, the proton profiles show apparent ring-like or filamented structures. The experimental results illustrate the current status of the SULF-10 PW beamline.

The on-target peak power of the SULF-10 PW beamline will be increased to 10 PW after maintenance of the pump sources in the last amplifier. Further optimization works to improve laser intensity and contrast are continuing through using a smaller f-number OAP and setting up a traditional PM. In the near future, the peak laser intensity is expected to reach 10²²–10²³ W/cm², which provides strong support for research in strong-field physics.