Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T08:03:06.500Z Has data issue: false hasContentIssue false
  • English
  • Français

WEAK CAYLEY TABLE GROUPS OF SOME CRYSTALLOGRAPHIC GROUPS

Part of: Representation theory of groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  28 January 2018

STEPHEN P. HUMPHRIES  and
REBECA A. PAULSEN
STEPHEN P. HUMPHRIES
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT 84602, USA e-mail: [email protected], [email protected]
REBECA A. PAULSEN
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT 84602, USA e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a group G, a weak Cayley table isomorphism is a bijection f : G → G such that f(g1g2) is conjugate to f(g1)f(g2) for all g1, g2 ∈ G. The set of all weak Cayley table isomorphisms forms a group 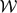(G) that is the group of symmetries of the weak Cayley table of G. We determine 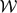(G) for each of the 17 wallpaper groups G, and for some other crystallographic groups.

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20C05: Group rings of finite groups and their modules 20F28: Automorphism groups of groups
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 60 , Issue 3 , September 2018 , pp. 635 - 660
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

References

REFERENCES

1. Curtis, C. W., Pioneers of representation theory: Frobenius, Burnside, Schur, and Brauer. History of mathematics, vol. 15 (American Mathematical Society, Providence, RI; London Mathematical Society, London, 1999), 287 pages.Google Scholar
2. Curtis, C. W. and Reiner, I., Representation theory of finite groups and associative algebras. (AMS Chelsea Publishing, Providence, RI, 2006). Reprint of the 1962 original.Google Scholar
3. Feit, W., Characters of finite groups (W. A. Benjamin, New York-Amsterdam 1967), viii+186 pp.Google Scholar
4. Gonçalves, D. and Wong, P., Automorphisms of the two dimensional crystallographic groups, Comm. Algebra 42 (2) (2014), 909–931.Google Scholar
5. Humphries, S. P., Weak Cayley table groups, J. Algebra 216 (1999), 135–158.Google Scholar
6. Humphries, S. P. and Long, N., Weak Cayley table groups: Alternating and coxeter groups, Comm. Algebra 43 (11) (2015), 4763–4782.CrossRefGoogle Scholar
7. Humphries, S. P. and Long, N., Weak Cayley table groups III: PSL(2,q), Comm. Algebra 45 (7) (2017), 3110–3136.Google Scholar
8. Iversen, B., Lectures on crystallographic groups. Lecture notes series, vol. 60 (Aarhus Universitet, Matematisk Institut, Aarhus, 1990), vi+144.Google Scholar
9. Janssen, T., Crystallographic groups (North-Holland Publishing Co., Amsterdam-London; American Elsevier Publishing Co., Inc., New York, 1973), xiii+281.Google Scholar
10. Johnson, K. W., Mattarei, S. and Sehgal, S. K., Weak Cayley tables, J. Lond. Math. Soc. 61 (2000), 395–411.Google Scholar
11. Bosma, W. and Cannon, J., MAGMA (University of Sydney, 1994).Google Scholar
12. Magnus, W., Karrass, S., and Solitar, D., Combinatorial group theory (Dover, New York, 1976).Google Scholar