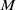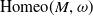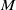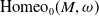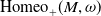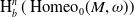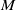1. Introduction
Let
![]() $M$
be an oriented connected smooth manifold. Suppose
$M$
be an oriented connected smooth manifold. Suppose
![]() $\omega$
is a finite measure induced by a volume form on
$\omega$
is a finite measure induced by a volume form on
![]() $M$
. In [Reference Brandenbursky and Marcinkowski5], we defined a homomorphism
$M$
. In [Reference Brandenbursky and Marcinkowski5], we defined a homomorphism
where
![]() $\operatorname{H}_b^\bullet (\operatorname{Homeo}_0\!(M,\omega ))$
is the bounded cohomology of a discrete group. The map
$\operatorname{H}_b^\bullet (\operatorname{Homeo}_0\!(M,\omega ))$
is the bounded cohomology of a discrete group. The map
![]() $\Gamma _b$
is a generalization of a map defined by Gambaudo and Ghys in the quasimorphism setting [Reference Gambaudo and Ghys10, Section 5].
$\Gamma _b$
is a generalization of a map defined by Gambaudo and Ghys in the quasimorphism setting [Reference Gambaudo and Ghys10, Section 5].
![]() $\Gamma _{\hspace{-2px}b}$
was used in [Reference Brandenbursky and Marcinkowski5] to show that the
$\Gamma _{\hspace{-2px}b}$
was used in [Reference Brandenbursky and Marcinkowski5] to show that the
![]() $3^{rd}$
bounded cohomology of
$3^{rd}$
bounded cohomology of
![]() $\operatorname{Homeo}_0\!(M,\omega )$
is infinite dimensional for many manifolds
$\operatorname{Homeo}_0\!(M,\omega )$
is infinite dimensional for many manifolds
![]() $M$
. In [Reference Nitsche19], more results concerning bounded cohomology, as well as standard cohomology, of
$M$
. In [Reference Nitsche19], more results concerning bounded cohomology, as well as standard cohomology, of
![]() $\operatorname{Homeo}_0\!(M,\omega )$
were obtained. Variations of
$\operatorname{Homeo}_0\!(M,\omega )$
were obtained. Variations of
![]() $\Gamma _b$
were used in [Reference Kimura15] to prove similar results concerning
$\Gamma _b$
were used in [Reference Kimura15] to prove similar results concerning
![]() $\operatorname{Diff}_0\!(S,area)$
, where
$\operatorname{Diff}_0\!(S,area)$
, where
![]() $S$
is a disc, sphere, or torus.
$S$
is a disc, sphere, or torus.
In this paper, we continue this line of research and focus on two important families of cohomology classes described below. Moreover, we construct an extension of
![]() $\Gamma _b$
to a map
$\Gamma _b$
to a map
where
![]() $\mathcal{M}(M,*)$
is the mapping class group of once punctured
$\mathcal{M}(M,*)$
is the mapping class group of once punctured
![]() $M$
(see Section 3.3). This extension is used to define the Euler class on
$M$
(see Section 3.3). This extension is used to define the Euler class on
![]() $\operatorname{Homeo}_+(S,\omega )$
for an oriented closed hyperbolic surface
$\operatorname{Homeo}_+(S,\omega )$
for an oriented closed hyperbolic surface
![]() $S$
, and we hope that it might be useful to study the cohomology of
$S$
, and we hope that it might be useful to study the cohomology of
![]() $\operatorname{Homeo}\!(M,\omega )$
for other manifolds
$\operatorname{Homeo}\!(M,\omega )$
for other manifolds
![]() $M$
.
$M$
.
The bounded volume class. Let
![]() $M$
be an oriented hyperbolic manifold, and let
$M$
be an oriented hyperbolic manifold, and let
![]() $\omega _h$
be the volume form induced by the hyperbolic metric. In this setting,
$\omega _h$
be the volume form induced by the hyperbolic metric. In this setting,
![]() $\omega _h$
defines a class
$\omega _h$
defines a class
![]() $Vol_M \in \operatorname{H}_b^n(\pi _1(M)) \simeq \operatorname{H}_b^n(M)$
(see Section 2.2). If
$Vol_M \in \operatorname{H}_b^n(\pi _1(M)) \simeq \operatorname{H}_b^n(M)$
(see Section 2.2). If
![]() $M$
is closed,
$M$
is closed,
![]() $Vol_M$
is a natural bounded representative of
$Vol_M$
is a natural bounded representative of
![]() $[\omega _h] \in \operatorname{H}_{dR}^n(M)$
.
$[\omega _h] \in \operatorname{H}_{dR}^n(M)$
.
Our main result positively answers the question in Section 5 of [Reference Brandenbursky and Marcinkowski5] for degree 2 and partially for degree 3. Moreover, it may be seen as a successful attempt to define a volume class in the bounded cohomology of an infinite dimensional transformation group.
Theorem 1.1.
Let
![]() $M$
be an oriented manifold of dimension
$M$
be an oriented manifold of dimension
![]() $n$
such that it is either:
$n$
such that it is either:
-
• A hyperbolic surface with a non-abelian fundamental group or
-
• A complete
 $3$
-dimensional hyperbolic manifold that fibers over the circle with a non-compact fiber.
$3$
-dimensional hyperbolic manifold that fibers over the circle with a non-compact fiber.
Suppose a measure
![]() $\omega$
is induced by a volume form on
$\omega$
is induced by a volume form on
![]() $M$
and
$M$
and
![]() $\omega$
is finite. Then the class
$\omega$
is finite. Then the class
![]() $\Gamma _{\hspace{-2px}b}(Vol_M) \in \operatorname{H}_b^n(\operatorname{Homeo}_0\!(M,\omega ))$
has positive norm and hence is non-trivial.
$\Gamma _{\hspace{-2px}b}(Vol_M) \in \operatorname{H}_b^n(\operatorname{Homeo}_0\!(M,\omega ))$
has positive norm and hence is non-trivial.
The class
![]() $Vol_M \in \operatorname{H}_b^n(M)$
was considered by Gromov and Thurston in the proof of the proportionality principle [Reference Gromov11, Reference Thurston21]. Moreover, it serves as a rich source for classes in
$Vol_M \in \operatorname{H}_b^n(M)$
was considered by Gromov and Thurston in the proof of the proportionality principle [Reference Gromov11, Reference Thurston21]. Moreover, it serves as a rich source for classes in
![]() $3^{rd}$
bounded cohomology of free and surface groups [Reference Soma20].
$3^{rd}$
bounded cohomology of free and surface groups [Reference Soma20].
It is worth mentioning that it is not known if the bounded cohomology in degree
![]() $n$
of a non-abelian free group for
$n$
of a non-abelian free group for
![]() $n\gt 3$
is non-trivial; hence, our proof works in dimension
$n\gt 3$
is non-trivial; hence, our proof works in dimension
![]() $2$
and sometimes in dimension
$2$
and sometimes in dimension
![]() $3$
so far. The problem of non-triviality of
$3$
so far. The problem of non-triviality of
![]() $\Gamma _b(Vol_M)$
for higher dimensional hyperbolic manifolds or closed hyperbolic
$\Gamma _b(Vol_M)$
for higher dimensional hyperbolic manifolds or closed hyperbolic
![]() $3$
-manifolds is still open.
$3$
-manifolds is still open.
The bounded Euler class. Let
![]() $S$
be a closed oriented surface and
$S$
be a closed oriented surface and
![]() $\omega$
a measure defined by an area form on
$\omega$
a measure defined by an area form on
![]() $S$
. Denote by
$S$
. Denote by
![]() $\operatorname{Homeo}_+(S,\omega )$
the subgroup of
$\operatorname{Homeo}_+(S,\omega )$
the subgroup of
![]() $\operatorname{Homeo}(S,\omega )$
of orientation preserving homeomorphisms.
$\operatorname{Homeo}(S,\omega )$
of orientation preserving homeomorphisms.
Let
![]() $* \in S$
be a point in
$* \in S$
be a point in
![]() $S$
and
$S$
and
![]() $\mathcal{M}_+(S,*)$
be the orientation preserving mapping class group of
$\mathcal{M}_+(S,*)$
be the orientation preserving mapping class group of
![]() $S\; \backslash \; \{*\}$
. Recall that
$S\; \backslash \; \{*\}$
. Recall that
![]() $\pi _1(S,*) \lt \mathcal{M}_+(S,*)$
due to the Birman exact sequence. As we will see in Section 3.3, the map
$\pi _1(S,*) \lt \mathcal{M}_+(S,*)$
due to the Birman exact sequence. As we will see in Section 3.3, the map
![]() $\Gamma _b$
can be extended to a map
$\Gamma _b$
can be extended to a map
![]() $\Gamma ^{{\scriptscriptstyle \mathcal{M}_+}}_b$
such that the following diagram commutes:
$\Gamma ^{{\scriptscriptstyle \mathcal{M}_+}}_b$
such that the following diagram commutes:

The vertical arrows are induced by inclusions. Thus, at the cost of passing to a bigger group
![]() $\mathcal{M}_+(S,*)$
, we can generate classes in the group of
$\mathcal{M}_+(S,*)$
, we can generate classes in the group of
![]() $\omega$
-preserving homeomorphisms of
$\omega$
-preserving homeomorphisms of
![]() $S$
not necessarily isotopic to the identity.
$S$
not necessarily isotopic to the identity.
Let
![]() $\operatorname{Homeo}_+(S^1)$
be the group of orientation preserving homeomorphisms of the circle, and let
$\operatorname{Homeo}_+(S^1)$
be the group of orientation preserving homeomorphisms of the circle, and let
![]() $e_b \in \operatorname{H}_b^2(\operatorname{Homeo}_+(S^1))$
be the bounded Euler class. There is a natural map
$e_b \in \operatorname{H}_b^2(\operatorname{Homeo}_+(S^1))$
be the bounded Euler class. There is a natural map
![]() $\alpha\ :\ \mathcal{M}_+(S,*) \to \operatorname{Homeo}_+(S^1)$
defined by the action of
$\alpha\ :\ \mathcal{M}_+(S,*) \to \operatorname{Homeo}_+(S^1)$
defined by the action of
![]() $\mathcal{M}_+(S,*) \simeq \operatorname{Aut}_+(\pi _1(S))$
on the Gromov boundary of
$\mathcal{M}_+(S,*) \simeq \operatorname{Aut}_+(\pi _1(S))$
on the Gromov boundary of
![]() $\pi _1(S)$
. Let
$\pi _1(S)$
. Let
![]() $e_b^{{\scriptscriptstyle \mathcal{M}_+}}$
and
$e_b^{{\scriptscriptstyle \mathcal{M}_+}}$
and
![]() $e_b^S$
be the pullbacks of
$e_b^S$
be the pullbacks of
![]() $e_b$
to
$e_b$
to
![]() $\mathcal{M}_+(S,*)$
and
$\mathcal{M}_+(S,*)$
and
![]() $\pi _1(S)$
.
$\pi _1(S)$
.
Theorem 1.2.
Let
![]() $S$
be a closed oriented surface of genus
$S$
be a closed oriented surface of genus
![]() $\geq 2$
, and
$\geq 2$
, and
![]() $\omega$
a measure induced by an area form on
$\omega$
a measure induced by an area form on
![]() $S$
. Then the classes
$S$
. Then the classes
![]() $\Gamma _b(e_b^S) \in \operatorname{H}_b^2(\operatorname{Homeo}_0(S,\omega ))$
and
$\Gamma _b(e_b^S) \in \operatorname{H}_b^2(\operatorname{Homeo}_0(S,\omega ))$
and
![]() $\Gamma _b^{{\scriptscriptstyle \mathcal{M}_+}}(e_b^{{\scriptscriptstyle \mathcal{M}_+}}) \in \operatorname{H}_b^2(\operatorname{Homeo}_+(S,\omega ))$
have positive norms and hence are non-trivial.
$\Gamma _b^{{\scriptscriptstyle \mathcal{M}_+}}(e_b^{{\scriptscriptstyle \mathcal{M}_+}}) \in \operatorname{H}_b^2(\operatorname{Homeo}_+(S,\omega ))$
have positive norms and hence are non-trivial.
We emphasize that in Theorems1.1 and in 1.2 one can take instead of
![]() $\operatorname{Homeo}_0\!(M,\omega )$
smaller groups like
$\operatorname{Homeo}_0\!(M,\omega )$
smaller groups like
![]() $\operatorname{Diff}_0(M,\omega )$
, or
$\operatorname{Diff}_0(M,\omega )$
, or
![]() $\operatorname{Symp}_0(S,\omega )$
or
$\operatorname{Symp}_0(S,\omega )$
or
![]() $\operatorname{Ham}(S)$
whenever
$\operatorname{Ham}(S)$
whenever
![]() $S$
is a hyperbolic surface, and the same results hold.
$S$
is a hyperbolic surface, and the same results hold.
On the proof and organization of the paper. The method of the proof is a refinement (and at the same time a simplification) of the one from [Reference Brandenbursky and Marcinkowski5]. In the case of bounded volume classes, it is based on mapping a non-abelian free group
![]() $F$
to
$F$
to
![]() $\pi _1(M)$
and to
$\pi _1(M)$
and to
![]() $\operatorname{Homeo}_0\!(M,\omega )$
, restricting
$\operatorname{Homeo}_0\!(M,\omega )$
, restricting
![]() $Vol_M$
and
$Vol_M$
and
![]() $\Gamma _b(Vol_M)$
to
$\Gamma _b(Vol_M)$
to
![]() $F$
and then comparing these two classes. An identical method is used for Euler classes. This technique is quite special since we do not know many subgroups of
$F$
and then comparing these two classes. An identical method is used for Euler classes. This technique is quite special since we do not know many subgroups of
![]() $\operatorname{Homeo}_0\!(M,\omega )$
. See [Reference Mann and Tshishiku18, Chapter 4] for a survey on realizations of groups by diffeomorphisms and homeomorphisms.
$\operatorname{Homeo}_0\!(M,\omega )$
. See [Reference Mann and Tshishiku18, Chapter 4] for a survey on realizations of groups by diffeomorphisms and homeomorphisms.
The outline of the paper is as follows. In Section 2.1, we give basic definitions of bounded cohomology. In Section 2.2, we define two versions of the volume class: the topological
![]() $Vol_M \in \operatorname{H}_b^n(M)$
and its group version
$Vol_M \in \operatorname{H}_b^n(M)$
and its group version
![]() $Vol_M^{gp} \in \operatorname{H}_b^n(\pi _1(M))$
. The topological version is well known, and we use it in the proofs. We need the group version because
$Vol_M^{gp} \in \operatorname{H}_b^n(\pi _1(M))$
. The topological version is well known, and we use it in the proofs. We need the group version because
![]() $\Gamma _b$
takes classes from the group cohomology. As expected,
$\Gamma _b$
takes classes from the group cohomology. As expected,
![]() $Vol_M$
and
$Vol_M$
and
![]() $Vol^{gp}_M$
define the same class under the canonical identification
$Vol^{gp}_M$
define the same class under the canonical identification
![]() $\operatorname{H}_b^n(M) \simeq \operatorname{H}_b^n(\pi _1(M))$
. We could not find a proof of this fact in the literature; thus, for completeness, we provide a detailed argument in Lemma 2.2. In Section 2.3, we define the Euler class in the mapping class group of a punctured surface. In Section 3, we define the maps
$\operatorname{H}_b^n(M) \simeq \operatorname{H}_b^n(\pi _1(M))$
. We could not find a proof of this fact in the literature; thus, for completeness, we provide a detailed argument in Lemma 2.2. In Section 2.3, we define the Euler class in the mapping class group of a punctured surface. In Section 3, we define the maps
![]() $\Gamma _b$
and
$\Gamma _b$
and
![]() $\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
. In Section 4, we show that for hyperbolic surfaces and certain
$\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
. In Section 4, we show that for hyperbolic surfaces and certain
![]() $3$
-dimensional hyperbolic manifolds, the class
$3$
-dimensional hyperbolic manifolds, the class
![]() $Vol_M$
restricts non-trivially to a free subgroup of
$Vol_M$
restricts non-trivially to a free subgroup of
![]() $\pi _1(M)$
. The same result holds for Euler classes and closed surfaces of genus
$\pi _1(M)$
. The same result holds for Euler classes and closed surfaces of genus
![]() $\geq 2$
. In Section 5, we give a simpler and at the same time more general version of a technical Lemma 3.1 from [Reference Brandenbursky and Marcinkowski5] and prove the main theorems. In Section 6, we discuss the case when
$\geq 2$
. In Section 5, we give a simpler and at the same time more general version of a technical Lemma 3.1 from [Reference Brandenbursky and Marcinkowski5] and prove the main theorems. In Section 6, we discuss the case when
![]() $\omega$
is the Dirac measure.
$\omega$
is the Dirac measure.
2. Preliminaries
2.1. Bounded cohomology
Let us give the definitions of bounded cohomology of a group and a space.
Let
![]() $G$
be a group. The space of bounded
$G$
be a group. The space of bounded
![]() $n$
-cochains is defined by
$n$
-cochains is defined by
Let
![]() $d_n$
be the ordinary coboundary operator
$d_n$
be the ordinary coboundary operator
![]() $d_n\ :\ \operatorname{C}^n_b(G) \to \operatorname{C}^{n+1}_b(G)$
. The group
$d_n\ :\ \operatorname{C}^n_b(G) \to \operatorname{C}^{n+1}_b(G)$
. The group
![]() $G$
acts on
$G$
acts on
![]() $\operatorname{C}^n_b(G)$
by
$\operatorname{C}^n_b(G)$
by
Let
![]() $\operatorname{C}^n_b(G)^G$
be the space of
$\operatorname{C}^n_b(G)^G$
be the space of
![]() $G$
-invariant cochains. The bounded cohomology of
$G$
-invariant cochains. The bounded cohomology of
![]() $G$
, denoted by
$G$
, denoted by
![]() $\operatorname{H}^\bullet _b(G)$
, is the homology of the cochain complex
$\operatorname{H}^\bullet _b(G)$
, is the homology of the cochain complex
![]() $\{\operatorname{C}^n_b(G)^G,d_n\}$
. Note that
$\{\operatorname{C}^n_b(G)^G,d_n\}$
. Note that
![]() $\operatorname{C}_b^n(G)^G$
is a subcomplex of the space of all
$\operatorname{C}_b^n(G)^G$
is a subcomplex of the space of all
![]() $G$
-invariant cochains; hence, we have a map
$G$
-invariant cochains; hence, we have a map
![]() $\operatorname{H}_b^n(G) \to \operatorname{H}^n(G,\mathbb{R})$
called the comparison map.
$\operatorname{H}_b^n(G) \to \operatorname{H}^n(G,\mathbb{R})$
called the comparison map.
On
![]() $\operatorname{C}^n_b(G)$
, we have the supremum norm denoted by
$\operatorname{C}^n_b(G)$
, we have the supremum norm denoted by
![]() $|\hspace{-1px}|\hspace{-3px}\cdot \hspace{-3px}|\hspace{-1px}|$
. This norm induces a semi-norm on
$|\hspace{-1px}|\hspace{-3px}\cdot \hspace{-3px}|\hspace{-1px}|$
. This norm induces a semi-norm on
![]() $\operatorname{H}^n_b(G)$
; that is, if
$\operatorname{H}^n_b(G)$
; that is, if
![]() $C \in \operatorname{H}_b^n(G)$
, then
$C \in \operatorname{H}_b^n(G)$
, then
Let
![]() $M$
be a topological space. A singular simplex is a continuous map from the standard simplex to
$M$
be a topological space. A singular simplex is a continuous map from the standard simplex to
![]() $M$
. By
$M$
. By
![]() $\operatorname{C}_n(M)$
, we denote the space of singular chains and by
$\operatorname{C}_n(M)$
, we denote the space of singular chains and by
![]() $\operatorname{S}_n(M) \subset \operatorname{C}_n(M)$
the set of all singular simplices in
$\operatorname{S}_n(M) \subset \operatorname{C}_n(M)$
the set of all singular simplices in
![]() $M$
. Let
$M$
. Let
![]() $\operatorname{C}^n_b(M)$
be the set of linear functions from
$\operatorname{C}^n_b(M)$
be the set of linear functions from
![]() $\operatorname{C}_n(M)$
to the reals that are bounded on
$\operatorname{C}_n(M)$
to the reals that are bounded on
![]() $\operatorname{S}_n(M)$
. Since
$\operatorname{S}_n(M)$
. Since
![]() $\operatorname{S}_n(M)$
generates
$\operatorname{S}_n(M)$
generates
![]() $\operatorname{C}_n(M)$
, one can think of an element in
$\operatorname{C}_n(M)$
, one can think of an element in
![]() $\operatorname{C}_n^b(M)$
as a bounded function
$\operatorname{C}_n^b(M)$
as a bounded function
![]() $c\ :\ \operatorname{S}_n(M) \to \mathbb{R}$
.
$c\ :\ \operatorname{S}_n(M) \to \mathbb{R}$
.
The bounded cohomology of
![]() $M$
, denoted by
$M$
, denoted by
![]() $\operatorname{H}^\bullet _b(M)$
, is the homology of the cochain complex
$\operatorname{H}^\bullet _b(M)$
, is the homology of the cochain complex
![]() $\{\operatorname{C}^n_b(M),d_n\}$
, where
$\{\operatorname{C}^n_b(M),d_n\}$
, where
![]() $d_n\ :\ \operatorname{C}^n_b(M) \to \operatorname{C}^{n+1}_b(M)$
is the standard coboundary operator. Like in the group case, we have the semi-norm and the comparison map. Sometimes it is convenient to work in the universal cover of
$d_n\ :\ \operatorname{C}^n_b(M) \to \operatorname{C}^{n+1}_b(M)$
is the standard coboundary operator. Like in the group case, we have the semi-norm and the comparison map. Sometimes it is convenient to work in the universal cover of
![]() $M$
. Let us recall that on
$M$
. Let us recall that on
![]() $\operatorname{C}^n_b(\widetilde{M})$
, we have an action of
$\operatorname{C}^n_b(\widetilde{M})$
, we have an action of
![]() $G = \pi _1(M)$
and
$G = \pi _1(M)$
and
![]() $\operatorname{C}^n_b(M)$
is naturally isomorphic to
$\operatorname{C}^n_b(M)$
is naturally isomorphic to
![]() $\operatorname{C}^n_b(\widetilde{M})^G$
.
$\operatorname{C}^n_b(\widetilde{M})^G$
.
We point out that bounded cohomology cannot be defined in terms of simplicial cochains (given some triangulation of
![]() $M$
). For example, if the triangulation is finite, then every simplicial cochain is bounded, and we get the standard cohomology.
$M$
). For example, if the triangulation is finite, then every simplicial cochain is bounded, and we get the standard cohomology.
In this paper, the manifold
![]() $M$
is aspherical. In this case,
$M$
is aspherical. In this case,
![]() $\operatorname{H}_b^n(\pi _1(M))$
is canonically isometric to
$\operatorname{H}_b^n(\pi _1(M))$
is canonically isometric to
![]() $\operatorname{H}_b^n(M)$
. See [Reference Frigerio9, Chapter 5] for a relatively elementary proof of this fact. It is based on an appropriate notion of resolution for bounded cohomology. Note that by the remarkable Mapping Theorem of Gromov, the assumption on asphericity of
$\operatorname{H}_b^n(M)$
. See [Reference Frigerio9, Chapter 5] for a relatively elementary proof of this fact. It is based on an appropriate notion of resolution for bounded cohomology. Note that by the remarkable Mapping Theorem of Gromov, the assumption on asphericity of
![]() $M$
can be dropped, but the proof of this fact is much harder [Reference Gromov11].
$M$
can be dropped, but the proof of this fact is much harder [Reference Gromov11].
2.2. The bounded volume class
In this paper, a hyperbolic manifold is a manifold (with or without boundary) whose all sectiontal curvatures equal
![]() $-1$
. In particular, we do not assume a hyperbolic manifold to be complete. Let
$-1$
. In particular, we do not assume a hyperbolic manifold to be complete. Let
![]() $M$
be a connected, oriented, and aspherical hyperbolic
$M$
be a connected, oriented, and aspherical hyperbolic
![]() $n$
-manifold. Below, we recall the definition of
$n$
-manifold. Below, we recall the definition of
![]() $Vol_M$
and give a detailed description of its counterpart in the group cohomology
$Vol_M$
and give a detailed description of its counterpart in the group cohomology
![]() $\operatorname{H}_b^n(\pi _1(M))$
, which seems to be less known. In Lemma 2.2, we show that both versions give the same class under the canonical identification of
$\operatorname{H}_b^n(\pi _1(M))$
, which seems to be less known. In Lemma 2.2, we show that both versions give the same class under the canonical identification of
![]() $\operatorname{H}_b^n(M)$
and
$\operatorname{H}_b^n(M)$
and
![]() $\operatorname{H}_b^n(\pi _1(M))$
.
$\operatorname{H}_b^n(\pi _1(M))$
.
We start with defining the volume class in the cohomology of a group. Let
![]() $Iso_+(\mathbb{H}^n)$
denote the group of orientation preserving isometries of the hyperbolic
$Iso_+(\mathbb{H}^n)$
denote the group of orientation preserving isometries of the hyperbolic
![]() $n$
-space, and let
$n$
-space, and let
![]() $vol_h$
be the hyperbolic volume form on
$vol_h$
be the hyperbolic volume form on
![]() $\mathbb{H}^n$
. Fix
$\mathbb{H}^n$
. Fix
![]() $* \in \mathbb{H}^n$
and for a tuple of elements
$* \in \mathbb{H}^n$
and for a tuple of elements
![]() $\bar{g} = (g_0,\ldots, g_n)$
in
$\bar{g} = (g_0,\ldots, g_n)$
in
![]() $Iso_+(\mathbb{H})$
consider the geodesic simplex
$Iso_+(\mathbb{H})$
consider the geodesic simplex
![]() $\Delta _{\bar{g}} \subset \mathbb{H}^n$
spanned by the points
$\Delta _{\bar{g}} \subset \mathbb{H}^n$
spanned by the points
![]() $g_0(*),\ldots, g_n(*)$
. This simplex can be parametrized using the barycentric coordinates [Reference Thurston21, Chapter 6]. Therefore, we regard
$g_0(*),\ldots, g_n(*)$
. This simplex can be parametrized using the barycentric coordinates [Reference Thurston21, Chapter 6]. Therefore, we regard
![]() $\Delta _{\bar{g}}$
as a map from the standard simplex to
$\Delta _{\bar{g}}$
as a map from the standard simplex to
![]() $\mathbb{H}^n$
. We define
$\mathbb{H}^n$
. We define
Note that
![]() $v(\bar{g})$
is the signed volume of
$v(\bar{g})$
is the signed volume of
![]() $\Delta _{\bar{g}}$
. Moreover,
$\Delta _{\bar{g}}$
. Moreover,
![]() $v$
is an
$v$
is an
![]() $Iso_+(\mathbb{H}^n)$
-invariant cocycle. Since volumes of geodesic simplices are bounded,
$Iso_+(\mathbb{H}^n)$
-invariant cocycle. Since volumes of geodesic simplices are bounded,
![]() $v$
is bounded and we can define:
$v$
is bounded and we can define:
For
![]() $G \lt Iso_+(\mathbb{H}^n)$
, we define
$G \lt Iso_+(\mathbb{H}^n)$
, we define
![]() $v_G$
to be the restriction of
$v_G$
to be the restriction of
![]() $v$
to
$v$
to
![]() $G$
and
$G$
and
![]() $Vol_G = [v_G] \in \operatorname{H}^n_b(G)$
.
$Vol_G = [v_G] \in \operatorname{H}^n_b(G)$
.
Recall that
![]() $M$
is a connected, oriented, and aspherical hyperbolic
$M$
is a connected, oriented, and aspherical hyperbolic
![]() $n$
-manifold. We allow
$n$
-manifold. We allow
![]() $M$
to have cusps or a boundary that is not totally geodesic. Represent
$M$
to have cusps or a boundary that is not totally geodesic. Represent
![]() $M$
as a quotient
$M$
as a quotient
![]() $M = X/\pi _1(M)$
where
$M = X/\pi _1(M)$
where
![]() $X \subset \mathbb{H}^n$
is contractible and
$X \subset \mathbb{H}^n$
is contractible and
![]() $\pi _1(M)$
acts on
$\pi _1(M)$
acts on
![]() $X$
by deck transformations. Note that the action of
$X$
by deck transformations. Note that the action of
![]() $\pi _1(M)$
on
$\pi _1(M)$
on
![]() $X$
extends uniquely to an action on
$X$
extends uniquely to an action on
![]() $\mathbb{H}^n$
. Denote this action by
$\mathbb{H}^n$
. Denote this action by
![]() $\rho\ :\ \pi _1(M) \to Iso_+(\mathbb{H}^n)$
. In what follows, we usually do not mention the representation
$\rho\ :\ \pi _1(M) \to Iso_+(\mathbb{H}^n)$
. In what follows, we usually do not mention the representation
![]() $\rho$
and regard
$\rho$
and regard
![]() $\pi _1(M)$
as a discrete subgroup of
$\pi _1(M)$
as a discrete subgroup of
![]() $Iso_+(\mathbb{H}^n)$
. To
$Iso_+(\mathbb{H}^n)$
. To
![]() $M$
, we associate the class
$M$
, we associate the class
and write
![]() $Vol_M^{gp} = Vol_{\rho (\pi _1(M))}$
. The action
$Vol_M^{gp} = Vol_{\rho (\pi _1(M))}$
. The action
![]() $\rho$
is well defined up to conjugacy; thus
$\rho$
is well defined up to conjugacy; thus
![]() $Vol_M^{gp}$
does not depend on
$Vol_M^{gp}$
does not depend on
![]() $\rho$
.
$\rho$
.
Let us now describe a singular cocycle that defines the class
![]() $Vol_M$
in
$Vol_M$
in
![]() $\operatorname{H}_b^n(M)$
. Let
$\operatorname{H}_b^n(M)$
. Let
![]() $\sigma$
be a singular simplex in
$\sigma$
be a singular simplex in
![]() $X \subset \mathbb{H}^n$
. The straightening
$X \subset \mathbb{H}^n$
. The straightening
![]() $str(\sigma )$
is the geodesic simplex with the same vertices as
$str(\sigma )$
is the geodesic simplex with the same vertices as
![]() $\sigma$
and parametrized using the barycentric coordinates (it is possible that
$\sigma$
and parametrized using the barycentric coordinates (it is possible that
![]() $str(\sigma )$
is not contained in
$str(\sigma )$
is not contained in
![]() $X$
). We define
$X$
). We define
We have that
![]() $v^{\prime }_M$
is a
$v^{\prime }_M$
is a
![]() $\pi _1(M)$
-invariant cocycle on
$\pi _1(M)$
-invariant cocycle on
![]() $X$
. It defines the bounded class
$X$
. It defines the bounded class
![]() $[v^{\prime }_M] \in \operatorname{H}_b^n(M)$
, which we denote by
$[v^{\prime }_M] \in \operatorname{H}_b^n(M)$
, which we denote by
![]() $Vol_M$
.
$Vol_M$
.
Hence we associate two classes to
![]() $M$
:
$M$
:
![]() $Vol_M$
in the cohomology of the space
$Vol_M$
in the cohomology of the space
![]() $M$
and a class
$M$
and a class
![]() $Vol_M^{gp}$
in the group cohomology of
$Vol_M^{gp}$
in the group cohomology of
![]() $\pi _1(M)$
.
$\pi _1(M)$
.
Remark 2.1.
The definition of
![]() $Vol_M$
can be generalized by integrating, instead of
$Vol_M$
can be generalized by integrating, instead of
![]() $vol_h$
, the pullback
$vol_h$
, the pullback
![]() $\tilde{\omega }$
of a closed
$\tilde{\omega }$
of a closed
![]() $k$
-form
$k$
-form
![]() $\omega$
on
$\omega$
on
![]() $M^n$
for
$M^n$
for
![]() $k \leq n$
(see Reference Barge and Ghys2, Reference Battista, Francaviglia, Moraschini, Sarti and Savini3). For a surface and
$k \leq n$
(see Reference Barge and Ghys2, Reference Battista, Francaviglia, Moraschini, Sarti and Savini3). For a surface and
![]() $2$
-forms such that
$2$
-forms such that
![]() $\tilde{\omega } = fvol_h$
for
$\tilde{\omega } = fvol_h$
for
![]() $f\gt 0$
, Theorem
1.1
holds with the same proof. As well, instead of a hyperbolic metric, one can take a pinched negatively curved metric on
$f\gt 0$
, Theorem
1.1
holds with the same proof. As well, instead of a hyperbolic metric, one can take a pinched negatively curved metric on
![]() $M$
, where one can straighten simplices. This should generate even more
$M$
, where one can straighten simplices. This should generate even more
![]() $Vol_M$
-like classes.
$Vol_M$
-like classes.
Lemma 2.2.
Let
![]() $M$
be a connected, oriented, and aspherical hyperbolic
$M$
be a connected, oriented, and aspherical hyperbolic
![]() $n$
-dimensional manifold, and let
$n$
-dimensional manifold, and let
![]() $r\ :\ \operatorname{H}_b^n(\pi _1(M)) \to \operatorname{H}_b^n(M)$
be the canonical isometric isomorphism. Then we have
$r\ :\ \operatorname{H}_b^n(\pi _1(M)) \to \operatorname{H}_b^n(M)$
be the canonical isometric isomorphism. Then we have
![]() $r(Vol_M^{gp}) = Vol_M$
.
$r(Vol_M^{gp}) = Vol_M$
.
Proof. Let
![]() $M = X/\pi _1(M)$
, where
$M = X/\pi _1(M)$
, where
![]() $X \subset \mathbb{H}^n$
. First, we shall show that without loss of generality, we can assume that
$X \subset \mathbb{H}^n$
. First, we shall show that without loss of generality, we can assume that
![]() $X = \mathbb{H}^n$
. Consider
$X = \mathbb{H}^n$
. Consider
![]() $M^{ex}= \mathbb{H}^n/\pi _1(M)$
. Since
$M^{ex}= \mathbb{H}^n/\pi _1(M)$
. Since
![]() $X\; \subset \; \mathbb{H}^n$
, we have that
$X\; \subset \; \mathbb{H}^n$
, we have that
![]() $M$
is a submanifold of
$M$
is a submanifold of
![]() $M^{ex}$
. Moreover,
$M^{ex}$
. Moreover,
![]() $M$
is aspherical, and by the Whitehead theorem, the inclusion
$M$
is aspherical, and by the Whitehead theorem, the inclusion
![]() $i\ :\ M \to M^{ex}$
is a homotopy equivalence. Hence
$i\ :\ M \to M^{ex}$
is a homotopy equivalence. Hence
is an isometric isomorphism. Moreover,
![]() $i^*(Vol_{M^{ex}}) = Vol_M$
. Thus instead of
$i^*(Vol_{M^{ex}}) = Vol_M$
. Thus instead of
![]() $M$
, we can consider
$M$
, we can consider
![]() $M^{ex}$
. In other words, we can assume that
$M^{ex}$
. In other words, we can assume that
![]() $X = \mathbb{H}^n$
.
$X = \mathbb{H}^n$
.
The explicit formula for
![]() $r$
can be found in [Reference Frigerio9, Lemma 5.2] (note that on the standard cohomology,
$r$
can be found in [Reference Frigerio9, Lemma 5.2] (note that on the standard cohomology,
![]() $r$
is just the map induced by the classifying map). We shall give a formula for the inverse of
$r$
is just the map induced by the classifying map). We shall give a formula for the inverse of
![]() $r$
.
$r$
.
Let
![]() $G = \pi _1(M)$
and
$G = \pi _1(M)$
and
![]() $* \in \mathbb{H}^n$
be a basepoint. Let
$* \in \mathbb{H}^n$
be a basepoint. Let
![]() $\Delta$
be the map which to each tuple
$\Delta$
be the map which to each tuple
![]() $\bar{g} = (g_0, \ldots, g_n) \in G^{n+1}$
associates
$\bar{g} = (g_0, \ldots, g_n) \in G^{n+1}$
associates
![]() $\Delta _{\bar{g}}$
, the geodesic simplex spanned by the
$\Delta _{\bar{g}}$
, the geodesic simplex spanned by the
![]() $g_i(*)$
and parametrized by barycentric coordinates.
$g_i(*)$
and parametrized by barycentric coordinates.
Consider the augmented cochain complexes
![]() $\{\operatorname{C}^\bullet _b(G),d\}$
and
$\{\operatorname{C}^\bullet _b(G),d\}$
and
![]() $\{\operatorname{C}_b^\bullet (\mathbb{H}^n)),d\}$
. It means that
$\{\operatorname{C}_b^\bullet (\mathbb{H}^n)),d\}$
. It means that
![]() $\operatorname{C}^{-1}_b(G) = \operatorname{C}_b^{-1}(\mathbb{H}) = \mathbb{R}$
and in both cases
$\operatorname{C}^{-1}_b(G) = \operatorname{C}_b^{-1}(\mathbb{H}) = \mathbb{R}$
and in both cases
![]() $d_{-1}$
maps a real number to a constant function. The map
$d_{-1}$
maps a real number to a constant function. The map
![]() $\Delta$
commutes with taking facets. That is, if
$\Delta$
commutes with taking facets. That is, if
![]() $\bar{f} \subset \bar{g}$
is an
$\bar{f} \subset \bar{g}$
is an
![]() $n$
-tuple in an
$n$
-tuple in an
![]() $(n+1)$
-tuple
$(n+1)$
-tuple
![]() $\bar{g}$
, then
$\bar{g}$
, then
![]() $\Delta _{\bar{f}}$
is just
$\Delta _{\bar{f}}$
is just
![]() $\Delta _{\bar{g}}$
restricted to the corresponding facet. Thus
$\Delta _{\bar{g}}$
restricted to the corresponding facet. Thus
![]() $\Delta$
induces a map of augmented cochain complexes
$\Delta$
induces a map of augmented cochain complexes
given by
![]() $\Delta ^*(c)(\bar{g}) = c(\Delta _{\bar{g}})$
and the identity on the augmentations. The map
$\Delta ^*(c)(\bar{g}) = c(\Delta _{\bar{g}})$
and the identity on the augmentations. The map
![]() $\Delta ^*$
is
$\Delta ^*$
is
![]() $G$
-invariant, and since these resolutions are relatively injective strong resolutions [Reference Frigerio9, Lemmas 4.12 and Lemma 5.4],
$G$
-invariant, and since these resolutions are relatively injective strong resolutions [Reference Frigerio9, Lemmas 4.12 and Lemma 5.4],
![]() $\Delta ^*$
induces a map
$\Delta ^*$
induces a map
which is the inverse of
![]() $r$
[Reference Frigerio9, Theorem 4.15]. Since
$r$
[Reference Frigerio9, Theorem 4.15]. Since
![]() $r$
is an isometric isomorphism, the same holds for
$r$
is an isometric isomorphism, the same holds for
![]() $\operatorname{H}^n_b(\Delta )$
. Moreover, it follows directly from the definitions that
$\operatorname{H}^n_b(\Delta )$
. Moreover, it follows directly from the definitions that
![]() $\Delta ^*(v^{\prime }_M) = v_G$
. Thus
$\Delta ^*(v^{\prime }_M) = v_G$
. Thus
![]() $r(Vol_M^{gp})\; =\; Vol_M$
.
$r(Vol_M^{gp})\; =\; Vol_M$
.
Let
![]() $\omega _h$
be the hyperbolic volume form on a closed hyperbolic manifold
$\omega _h$
be the hyperbolic volume form on a closed hyperbolic manifold
![]() $M$
. Let us point out that
$M$
. Let us point out that
![]() $[v^{\prime }_M] \in \operatorname{H}_b^n(M)$
goes to
$[v^{\prime }_M] \in \operatorname{H}_b^n(M)$
goes to
![]() $[\omega _h] \in \operatorname{H}_{dR}(M) \simeq H^n(M)$
after applying the comparison map. This can be seen by the straightening of simplices homotopy; see [Reference Thurston21] or [Reference Frigerio9, Lemma 8.12].
$[\omega _h] \in \operatorname{H}_{dR}(M) \simeq H^n(M)$
after applying the comparison map. This can be seen by the straightening of simplices homotopy; see [Reference Thurston21] or [Reference Frigerio9, Lemma 8.12].
2.3. Euler class in the mapping class group
Let
![]() $\operatorname{Homeo}_+^{\mathbb{Z}}(\mathbb{R})$
be the set of orientation preserving homeomorphisms
$\operatorname{Homeo}_+^{\mathbb{Z}}(\mathbb{R})$
be the set of orientation preserving homeomorphisms
![]() $f$
of
$f$
of
![]() $\mathbb{R}$
that are lifts of maps from
$\mathbb{R}$
that are lifts of maps from
![]() $\operatorname{Homeo}_+(S^1)$
. That is,
$\operatorname{Homeo}_+(S^1)$
. That is,
![]() $f(x+1) = f(x) + 1$
. It fits the central extension
$f(x+1) = f(x) + 1$
. It fits the central extension
The Euler class
![]() $e_b \in \operatorname{H}_b^2(\operatorname{Homeo}_+(S^1))$
is a particular bounded class representing the Euler class of this extension [Reference Frigerio9, Chapter 10]. Let
$e_b \in \operatorname{H}_b^2(\operatorname{Homeo}_+(S^1))$
is a particular bounded class representing the Euler class of this extension [Reference Frigerio9, Chapter 10]. Let
![]() $S$
be a closed oriented surface of genus
$S$
be a closed oriented surface of genus
![]() $\geq 2$
. On
$\geq 2$
. On
![]() $S$
, we fix a hyperbolic metric. Let
$S$
, we fix a hyperbolic metric. Let
![]() $\mathcal{M}_+(S,*)$
be the subgroup of
$\mathcal{M}_+(S,*)$
be the subgroup of
![]() $\mathcal{M}(S,*)$
of mapping classes represented by orientation preserving homeomorphisms. By the Dehn–Nielsen theorem
$\mathcal{M}(S,*)$
of mapping classes represented by orientation preserving homeomorphisms. By the Dehn–Nielsen theorem
![]() $\mathcal{M}_+(S,*) \simeq \operatorname{Aut}_+(\pi _1(S,*))$
; thus
$\mathcal{M}_+(S,*) \simeq \operatorname{Aut}_+(\pi _1(S,*))$
; thus
![]() $\mathcal{M}_+(S,*)$
acts on the Gromov boundary
$\mathcal{M}_+(S,*)$
acts on the Gromov boundary
![]() $\partial \pi _1(S,*) \simeq S^1$
. Hence we have a map
$\partial \pi _1(S,*) \simeq S^1$
. Hence we have a map
In geometric terms,
![]() $\alpha$
is described as follows. Let
$\alpha$
is described as follows. Let
![]() $f \in \operatorname{Homeo}_+(S,*)$
represent an element
$f \in \operatorname{Homeo}_+(S,*)$
represent an element
![]() $\psi \in \mathcal{M}_+(S,*)$
. Let
$\psi \in \mathcal{M}_+(S,*)$
. Let
![]() $\tilde{*} \in \mathbb{H}^2$
be a fixed preimage of
$\tilde{*} \in \mathbb{H}^2$
be a fixed preimage of
![]() $*$
, and let
$*$
, and let
![]() $\tilde{f}$
be the lift of
$\tilde{f}$
be the lift of
![]() $f$
such that
$f$
such that
![]() $\tilde{f}(\tilde{*}) = \tilde{*}$
. Now
$\tilde{f}(\tilde{*}) = \tilde{*}$
. Now
![]() $\alpha (\psi )$
is the action of
$\alpha (\psi )$
is the action of
![]() $\tilde{f}$
on
$\tilde{f}$
on
![]() $\partial \mathbb{H}^2$
and it does not depend on the choice of
$\partial \mathbb{H}^2$
and it does not depend on the choice of
![]() $f$
representing
$f$
representing
![]() $\psi$
. Note that
$\psi$
. Note that
![]() $\alpha$
restricted to
$\alpha$
restricted to
![]() $\pi _1(S,*) \lt \mathcal{M}_+(S,*)$
is just the standard action on
$\pi _1(S,*) \lt \mathcal{M}_+(S,*)$
is just the standard action on
![]() $\partial \mathbb{H}^2$
by deck transformations.
$\partial \mathbb{H}^2$
by deck transformations.
Let
![]() $e_b^{{\scriptscriptstyle \mathcal{M}_+}} = \alpha ^*(e_b)$
and
$e_b^{{\scriptscriptstyle \mathcal{M}_+}} = \alpha ^*(e_b)$
and
![]() $e_b^S$
be the restriction of
$e_b^S$
be the restriction of
![]() $e_b^{{\scriptscriptstyle \mathcal{M}_+}}$
to
$e_b^{{\scriptscriptstyle \mathcal{M}_+}}$
to
![]() $\pi _1(S,*) \lt \mathcal{M}_+(S,*)$
. The class
$\pi _1(S,*) \lt \mathcal{M}_+(S,*)$
. The class
![]() $e_b^{{\scriptscriptstyle \mathcal{M}_+}}$
was studied in [Reference Chen7, Reference Jekel and Rolland13].
$e_b^{{\scriptscriptstyle \mathcal{M}_+}}$
was studied in [Reference Chen7, Reference Jekel and Rolland13].
3. Definitions of
 $\Gamma _{\hspace{-2px}b}$
and
$\Gamma _{\hspace{-2px}b}$
and
 $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
Suppose
![]() $M$
is a connected smooth manifold and
$M$
is a connected smooth manifold and
![]() $\omega$
is a finite measure induced by a volume form. In this section, we define the maps
$\omega$
is a finite measure induced by a volume form. In this section, we define the maps
![]() $\Gamma _{\hspace{-2px}b}$
and
$\Gamma _{\hspace{-2px}b}$
and
![]() $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
(the latter for compact
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
(the latter for compact
![]() $M$
). We start with a geometrically motivated definition of
$M$
). We start with a geometrically motivated definition of
![]() $\Gamma _{\hspace{-2px}b}$
by a system of paths. This definition naturally leads to the definition of
$\Gamma _{\hspace{-2px}b}$
by a system of paths. This definition naturally leads to the definition of
![]() $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
by a system of homeomorphisms. To show that the definitions of
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
by a system of homeomorphisms. To show that the definitions of
![]() $\Gamma _{\hspace{-2px}b}$
and
$\Gamma _{\hspace{-2px}b}$
and
![]() $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
do not depend on the chosen systems, we use a result from [Reference Nitsche19]. To this end, we rephrase our definitions in the language of couplings. In the case of
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
do not depend on the chosen systems, we use a result from [Reference Nitsche19]. To this end, we rephrase our definitions in the language of couplings. In the case of
![]() $\Gamma _{\hspace{-2px}b}$
, the obvious coupling is given by the universal cover. For the convenience of the reader, we give the details in Section 3.2. It turns out that
$\Gamma _{\hspace{-2px}b}$
, the obvious coupling is given by the universal cover. For the convenience of the reader, we give the details in Section 3.2. It turns out that
![]() $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
can be described in the language of couplings as well. However, one needs to use a bigger (and therefore disconnected) cover of
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
can be described in the language of couplings as well. However, one needs to use a bigger (and therefore disconnected) cover of
![]() $M$
(see Section 3.4).
$M$
(see Section 3.4).
Fix a basepoint
![]() $* \in M$
. In this section, we assume that
$* \in M$
. In this section, we assume that
![]() $\pi _1(M,*)$
is center free. It holds for all manifolds we are interested in and with this assumption the construction of
$\pi _1(M,*)$
is center free. It holds for all manifolds we are interested in and with this assumption the construction of
![]() $\Gamma _{\hspace{-2px}b}$
and
$\Gamma _{\hspace{-2px}b}$
and
![]() $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
is slightly simpler.
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
is slightly simpler.
Let
![]() $p\ :\ \widetilde{M} \to M$
be the universal cover of
$p\ :\ \widetilde{M} \to M$
be the universal cover of
![]() $M$
. We view an element
$M$
. We view an element
![]() $l \in p^{-1}(x)$
as a homotopy class relative to
$l \in p^{-1}(x)$
as a homotopy class relative to
![]() $\{*,x\}$
of a path connecting
$\{*,x\}$
of a path connecting
![]() $*$
to
$*$
to
![]() $x$
. The action of
$x$
. The action of
![]() $\pi _1(M,*)$
on
$\pi _1(M,*)$
on
![]() $\widetilde{M}$
is given by concatenating a loop representing
$\widetilde{M}$
is given by concatenating a loop representing
![]() $\gamma \in \pi _1(M,*)$
and a path representing
$\gamma \in \pi _1(M,*)$
and a path representing
![]() $l \in \widetilde{M}$
.
$l \in \widetilde{M}$
.
Recall that
![]() $\operatorname{Homeo}(M)$
is the group of all homeomorphisms of
$\operatorname{Homeo}(M)$
is the group of all homeomorphisms of
![]() $M$
and
$M$
and
![]() $\operatorname{Homeo}_0(M)$
are those elements of
$\operatorname{Homeo}_0(M)$
are those elements of
![]() $\operatorname{Homeo}(M)$
that are isotopic to the identity of
$\operatorname{Homeo}(M)$
that are isotopic to the identity of
![]() $M$
. Similarly,
$M$
. Similarly,
![]() $\operatorname{Homeo}\!(M,\omega )$
is the group of all homeomorphims of
$\operatorname{Homeo}\!(M,\omega )$
is the group of all homeomorphims of
![]() $M$
preserving
$M$
preserving
![]() $\omega$
and
$\omega$
and
![]() $\operatorname{Homeo}_0\!(M,\omega )$
are those elements of
$\operatorname{Homeo}_0\!(M,\omega )$
are those elements of
![]() $\operatorname{Homeo}\!(M,\omega )$
that are isotopic to the identity of
$\operatorname{Homeo}\!(M,\omega )$
that are isotopic to the identity of
![]() $M$
via
$M$
via
![]() $\omega$
-preserving maps.
$\omega$
-preserving maps.
In all these transformation groups, we consider their right group action on
![]() $M$
so that
$M$
so that
![]() $fg$
acts by
$fg$
acts by
![]() $(fg)(x) = g(f(x))$
for all
$(fg)(x) = g(f(x))$
for all
![]() $x \in M$
. We are forced to use this convention since later in Section 3.3, we relate elements of
$x \in M$
. We are forced to use this convention since later in Section 3.3, we relate elements of
![]() $\pi _1(M,*)$
to homeomorphisms in
$\pi _1(M,*)$
to homeomorphisms in
![]() $\operatorname{Homeo}(M)$
using a push map, and we want the multiplication in
$\operatorname{Homeo}(M)$
using a push map, and we want the multiplication in
![]() $\pi _1(M,*)$
to be compatible with how we compose homeomorphisms.
$\pi _1(M,*)$
to be compatible with how we compose homeomorphisms.
Recall that a left action of a group
![]() $G$
on a set
$G$
on a set
![]() $X$
is a homomorphism
$X$
is a homomorphism
![]() $G \to \operatorname{Aut}(X)$
and a right action is an antihomomorphism
$G \to \operatorname{Aut}(X)$
and a right action is an antihomomorphism
![]() $G \to \operatorname{Aut}(X)$
. On
$G \to \operatorname{Aut}(X)$
. On
![]() $\operatorname{Aut}(X)$
, we compose maps starting from the right-most. In this way, we have a left action of
$\operatorname{Aut}(X)$
, we compose maps starting from the right-most. In this way, we have a left action of
![]() $\pi _1(M,*)$
on
$\pi _1(M,*)$
on
![]() $\widetilde{M}$
and a right action of
$\widetilde{M}$
and a right action of
![]() $\operatorname{Homeo}(M)$
on
$\operatorname{Homeo}(M)$
on
![]() $M$
.
$M$
.
3.1. Description of
 $\Gamma _{\hspace{-2px}b}$
$\Gamma _{\hspace{-2px}b}$
In this paragraph, we give the simplest, in our opinion, description of
![]() $\Gamma _{\hspace{-2px}b}$
. A more refined and general definition can be found in [Reference Brandenbursky and Marcinkowski5]. Another approach based on coupling of groups is given in [Reference Nitsche19]. Note that the definition in [Reference Nitsche19] is much more general and works for measurable spaces and groups of measurable transformations.
$\Gamma _{\hspace{-2px}b}$
. A more refined and general definition can be found in [Reference Brandenbursky and Marcinkowski5]. Another approach based on coupling of groups is given in [Reference Nitsche19]. Note that the definition in [Reference Nitsche19] is much more general and works for measurable spaces and groups of measurable transformations.
Let
![]() $s_x$
be a path connecting
$s_x$
be a path connecting
![]() $*$
to
$*$
to
![]() $x \in M$
. By
$x \in M$
. By
![]() $[s_x]$
, we denote the homotopy class of
$[s_x]$
, we denote the homotopy class of
![]() $s_x$
relative to the endpoints
$s_x$
relative to the endpoints
![]() $\{*,x\}$
, and by
$\{*,x\}$
, and by
![]() $\bar{s}_x$
, we denote the reverse of
$\bar{s}_x$
, we denote the reverse of
![]() $s_x$
. A system of paths for
$s_x$
. A system of paths for
![]() $M$
is a function on
$M$
is a function on
![]() $M$
of the form
$M$
of the form
![]() $S(x) = [s_x]$
, where
$S(x) = [s_x]$
, where
![]() $s_x$
is any path connecting
$s_x$
is any path connecting
![]() $*$
to
$*$
to
![]() $x$
.
$x$
.
Assume
![]() $S$
is a system of paths. We shall define a map
$S$
is a system of paths. We shall define a map
Let
![]() $S(x)$
be represented by a path
$S(x)$
be represented by a path
![]() $s_x$
. Fix
$s_x$
. Fix
![]() $f \in \operatorname{Homeo}_0\!(M,\omega )$
and
$f \in \operatorname{Homeo}_0\!(M,\omega )$
and
![]() $f_t$
an isotopy connecting
$f_t$
an isotopy connecting
![]() $Id_M$
to
$Id_M$
to
![]() $f$
. We define
$f$
. We define
![]() $\gamma (f,x) \in \pi _1(M,*)$
to be the homotopy class of the loop based at
$\gamma (f,x) \in \pi _1(M,*)$
to be the homotopy class of the loop based at
![]() $*$
which is the concatenation of
$*$
which is the concatenation of
![]() $s_x$
, the trajectory
$s_x$
, the trajectory
![]() $f_t(x)$
and
$f_t(x)$
and
![]() $\bar{s}_{f(x)}$
. The element
$\bar{s}_{f(x)}$
. The element
![]() $\gamma (f,x)$
does not depend on the choice of paths representing
$\gamma (f,x)$
does not depend on the choice of paths representing
![]() $S(x)$
and
$S(x)$
and
![]() $S(f(x))$
. Moreover,
$S(f(x))$
. Moreover,
![]() $\gamma (f,x)$
does not depend on the isotopy
$\gamma (f,x)$
does not depend on the isotopy
![]() $f_t$
. Indeed, it follows from [Reference Brandenbursky and Marcinkowski5, Proposition 3.1] that changing the isotopy
$f_t$
. Indeed, it follows from [Reference Brandenbursky and Marcinkowski5, Proposition 3.1] that changing the isotopy
![]() $f_t$
to another isotopy connecting
$f_t$
to another isotopy connecting
![]() $Id_M$
and
$Id_M$
and
![]() $f$
would change
$f$
would change
![]() $\gamma (f,x)$
by an element of the center of
$\gamma (f,x)$
by an element of the center of
![]() $\pi _1(M,*)$
. Since we assumed that the center of
$\pi _1(M,*)$
. Since we assumed that the center of
![]() $\pi _1(M,*)$
is trivial,
$\pi _1(M,*)$
is trivial,
![]() $\gamma (f,x)$
is well defined. Note that
$\gamma (f,x)$
is well defined. Note that
![]() $\gamma$
depends on the choice of the system of paths
$\gamma$
depends on the choice of the system of paths
![]() $S$
.
$S$
.
It is a simple calculation that
![]() $\gamma$
satisfies a cocycle condition in the following form:
$\gamma$
satisfies a cocycle condition in the following form:
Define
![]() $\widetilde{\omega }$
to be the measure on
$\widetilde{\omega }$
to be the measure on
![]() $\widetilde{M}$
induced by the pullback of the volume form on
$\widetilde{M}$
induced by the pullback of the volume form on
![]() $M$
that defines
$M$
that defines
![]() $\omega$
. Since elements of
$\omega$
. Since elements of
![]() $\widetilde{M}$
are homotopy classes relative to the endpoints of paths in
$\widetilde{M}$
are homotopy classes relative to the endpoints of paths in
![]() $M$
starting at
$M$
starting at
![]() $*$
, the image
$*$
, the image
![]() $im(S)$
is a subset of
$im(S)$
is a subset of
![]() $\widetilde{M}$
. We say that
$\widetilde{M}$
. We say that
![]() $S$
is measurable if
$S$
is measurable if
![]() $im(S)$
is
$im(S)$
is
![]() $\widetilde{\omega }$
-measurable. In Section 3.2, we show that measurable systems of paths exist.
$\widetilde{\omega }$
-measurable. In Section 3.2, we show that measurable systems of paths exist.
Now assume
![]() $S$
is a measurable system of paths. For each
$S$
is a measurable system of paths. For each
![]() $n$
, we define
$n$
, we define
to be the map induced by the following function defined on cochains (called again
![]() $\Gamma _{\hspace{-2px}b}$
):
$\Gamma _{\hspace{-2px}b}$
):
In Section 3.2, we show that the function under the integral is measurable and that
![]() $\Gamma _b$
does not depend on the choice of a measurable system of paths.
$\Gamma _b$
does not depend on the choice of a measurable system of paths.
Remark 3.1.
In [Reference Brandenbursky and Marcinkowski5], the group
![]() $\operatorname{Homeo}_0\!(M,\omega )$
is defined like in this paper with an additional assumption that homeomorphisms have compact support. This additional assumption was needed to define an analog of
$\operatorname{Homeo}_0\!(M,\omega )$
is defined like in this paper with an additional assumption that homeomorphisms have compact support. This additional assumption was needed to define an analog of
![]() $\Gamma _b$
for the ordinary cohomology in [Reference Brandenbursky and Marcinkowski5
, Section 3.4]. In this paper, we deal only with the bounded cohomology; therefore, we do not assume that elements of
$\Gamma _b$
for the ordinary cohomology in [Reference Brandenbursky and Marcinkowski5
, Section 3.4]. In this paper, we deal only with the bounded cohomology; therefore, we do not assume that elements of
![]() $\operatorname{Homeo}_0\!(M,\omega )$
are compactly supported. Moreover, contrary to [Reference Brandenbursky and Marcinkowski5], here we do not assume that
$\operatorname{Homeo}_0\!(M,\omega )$
are compactly supported. Moreover, contrary to [Reference Brandenbursky and Marcinkowski5], here we do not assume that
![]() $M$
carries a complete Riemannian metric.
$M$
carries a complete Riemannian metric.
Example 3.2.
Now we explicitly describe a cocycle representing the element
![]() $\Gamma _{\hspace{-2px}b}(Vol_M^{gp})$
. Let
$\Gamma _{\hspace{-2px}b}(Vol_M^{gp})$
. Let
![]() $M = X/\pi _1(M)$
, where
$M = X/\pi _1(M)$
, where
![]() $X \subset \mathbb{H}^n$
, and let
$X \subset \mathbb{H}^n$
, and let
![]() $\omega$
be any finite measure induced by a volume form on
$\omega$
be any finite measure induced by a volume form on
![]() $M$
. Assume that
$M$
. Assume that
![]() $\pi _1(M)$
has trivial center (equivalently,
$\pi _1(M)$
has trivial center (equivalently,
![]() $\pi _1(M)$
is not abelian, e.g.,
$\pi _1(M)$
is not abelian, e.g.,
![]() $M$
is not a quotient of
$M$
is not a quotient of
![]() $\mathbb{H}^n$
by a
$\mathbb{H}^n$
by a
![]() $\mathbb{Z}$
-action). Let
$\mathbb{Z}$
-action). Let
![]() $\tilde{*} \in X$
be a lift of the basepoint
$\tilde{*} \in X$
be a lift of the basepoint
![]() $*$
and
$*$
and
![]() $f_0,\ldots, f_n \in \operatorname{Homeo}_0\!(M,\omega )$
. For every
$f_0,\ldots, f_n \in \operatorname{Homeo}_0\!(M,\omega )$
. For every
![]() $x \in M$
, we get a tuple of elements
$x \in M$
, we get a tuple of elements
![]() $\gamma (f_0,x), \ldots, \gamma (f_n,x)$
in
$\gamma (f_0,x), \ldots, \gamma (f_n,x)$
in
![]() $\pi _1(M)$
that act on
$\pi _1(M)$
that act on
![]() $X$
. Consider the points
$X$
. Consider the points
![]() $v_i(x) = \gamma (f_i,x)\tilde{*}$
and span a geodesic simplex
$v_i(x) = \gamma (f_i,x)\tilde{*}$
and span a geodesic simplex
![]() $\Delta (x)$
in
$\Delta (x)$
in
![]() $X$
with vertices
$X$
with vertices
![]() $v_i(x)$
. Now
$v_i(x)$
. Now
![]() $\Gamma _{\hspace{-2px}b}(Vol_M^{gp})$
is represented by a cocycle that assigns to
$\Gamma _{\hspace{-2px}b}(Vol_M^{gp})$
is represented by a cocycle that assigns to
![]() $(f_0,\ldots, f_n)$
the average signed volume of
$(f_0,\ldots, f_n)$
the average signed volume of
![]() $\Delta (x)$
over
$\Delta (x)$
over
![]() $M$
with respect to
$M$
with respect to
![]() $\omega$
.
$\omega$
.
3.2.
 $\Gamma _b$
via coupling
$\Gamma _b$
via coupling
Let us describe the construction of
![]() $\Gamma _b$
via couplings given in [Reference Nitsche19]. A coupling is a measured space
$\Gamma _b$
via couplings given in [Reference Nitsche19]. A coupling is a measured space
![]() $(X,\mu )$
together with a
$(X,\mu )$
together with a
![]() $\mu$
-preserving left action of a group
$\mu$
-preserving left action of a group
![]() $\Gamma$
and a commuting
$\Gamma$
and a commuting
![]() $\mu$
-preserving right action of a group
$\mu$
-preserving right action of a group
![]() $\Lambda$
. Suppose that
$\Lambda$
. Suppose that
![]() $\Gamma$
is countable, the action of
$\Gamma$
is countable, the action of
![]() $\Gamma$
is free, and
$\Gamma$
is free, and
![]() $F \subset X$
is a strict measurable fundamental domain for an action of
$F \subset X$
is a strict measurable fundamental domain for an action of
![]() $\Gamma$
. A map
$\Gamma$
. A map
![]() $\chi\ :\ X \to \Gamma$
is defined by the equation
$\chi\ :\ X \to \Gamma$
is defined by the equation
![]() $\chi (\gamma .x)=\gamma$
for
$\chi (\gamma .x)=\gamma$
for
![]() $x \in F$
and
$x \in F$
and
![]() $\gamma \in \Gamma$
. Note that
$\gamma \in \Gamma$
. Note that
![]() $\chi$
is measurable; that is, the preimage of every element in
$\chi$
is measurable; that is, the preimage of every element in
![]() $\Gamma$
is a measurable set. A function
$\Gamma$
is a measurable set. A function
![]() $\bar{\chi }\ :\ \Lambda \times F \to \Gamma$
given by
$\bar{\chi }\ :\ \Lambda \times F \to \Gamma$
given by
![]() $\bar{\chi }(\lambda, x) = \chi (x.\lambda )$
induces a homomorphism
$\bar{\chi }(\lambda, x) = \chi (x.\lambda )$
induces a homomorphism
![]() $tr_\Gamma ^\Lambda X\ :\ \operatorname{H}_b^\bullet (\Gamma ) \to \operatorname{H}_b^\bullet (\Lambda )$
by the formula [Reference Nitsche19, Section 3]
$tr_\Gamma ^\Lambda X\ :\ \operatorname{H}_b^\bullet (\Gamma ) \to \operatorname{H}_b^\bullet (\Lambda )$
by the formula [Reference Nitsche19, Section 3]
The map
![]() $\bar{\chi }$
is a composition of measurable functions; hence, the function under the integral is measurable. Moreover,
$\bar{\chi }$
is a composition of measurable functions; hence, the function under the integral is measurable. Moreover,
![]() $tr_\Lambda ^\Gamma X$
does not depend on the choice of
$tr_\Lambda ^\Gamma X$
does not depend on the choice of
![]() $F$
[Reference Nitsche19, Lemma 3.3].
$F$
[Reference Nitsche19, Lemma 3.3].
Let
![]() $f \in \operatorname{Homeo}_0\!(M,\omega )$
and suppose
$f \in \operatorname{Homeo}_0\!(M,\omega )$
and suppose
![]() $f_t$
is an isotopy connecting the identity of
$f_t$
is an isotopy connecting the identity of
![]() $M$
to
$M$
to
![]() $f$
. Denote by
$f$
. Denote by
![]() $\widetilde{f}$
the endpoint of a lift of
$\widetilde{f}$
the endpoint of a lift of
![]() $f_t$
to
$f_t$
to
![]() $\widetilde{M}$
. Note that, again by [Reference Brandenbursky and Marcinkowski5, Proposition 3.1], and by the assumption that
$\widetilde{M}$
. Note that, again by [Reference Brandenbursky and Marcinkowski5, Proposition 3.1], and by the assumption that
![]() $\pi _1(M,*)$
has a trivial center,
$\pi _1(M,*)$
has a trivial center,
![]() $\widetilde{f}$
does not depend on the chosen isotopy
$\widetilde{f}$
does not depend on the chosen isotopy
![]() $f_t$
. Therefore, we have a right
$f_t$
. Therefore, we have a right
![]() $\widetilde{\omega }$
-preserving action of
$\widetilde{\omega }$
-preserving action of
![]() $\operatorname{Homeo}_0\!(M,\omega )$
on
$\operatorname{Homeo}_0\!(M,\omega )$
on
![]() $\widetilde{M}$
, given by
$\widetilde{M}$
, given by
![]() $x.f = \widetilde{f}(x)$
,
$x.f = \widetilde{f}(x)$
,
![]() $x \in \widetilde{M}$
. Note that
$x \in \widetilde{M}$
. Note that
![]() $x.f$
is represented by a path connecting
$x.f$
is represented by a path connecting
![]() $*$
to
$*$
to
![]() $x$
and then following the trajectory from
$x$
and then following the trajectory from
![]() $x$
to
$x$
to
![]() $f(x)$
given by
$f(x)$
given by
![]() $f_t(x)$
.
$f_t(x)$
.
Now we consider the following coupling:
![]() $X = (\widetilde{M},\widetilde{\omega })$
together with the left action of
$X = (\widetilde{M},\widetilde{\omega })$
together with the left action of
![]() $\Gamma = \pi _1(M,*)$
and the right action of
$\Gamma = \pi _1(M,*)$
and the right action of
![]() $\Lambda = \operatorname{Homeo}_0\!(M,\omega )$
. For this coupling, we have
$\Lambda = \operatorname{Homeo}_0\!(M,\omega )$
. For this coupling, we have
![]() $\Gamma _{\hspace{-2px}b} = tr_\Gamma ^\Lambda X$
. Indeed, if
$\Gamma _{\hspace{-2px}b} = tr_\Gamma ^\Lambda X$
. Indeed, if
![]() $S$
is a measurable system of paths,
$S$
is a measurable system of paths,
![]() $im(S)$
is a strict measurable fundamental domain of the
$im(S)$
is a strict measurable fundamental domain of the
![]() $\pi _1(M,*)$
-action, and vice versa, every measurable fundamental domain defines a measurable system of paths. Moreover, let
$\pi _1(M,*)$
-action, and vice versa, every measurable fundamental domain defines a measurable system of paths. Moreover, let
![]() $S$
be a measurable system of paths and
$S$
be a measurable system of paths and
![]() $F=im(S)$
. Recall that
$F=im(S)$
. Recall that
![]() $p\ :\ \widetilde{M} \to M$
is the universal covering map. If
$p\ :\ \widetilde{M} \to M$
is the universal covering map. If
![]() $\gamma$
and
$\gamma$
and
![]() $\bar{\chi }$
are defined by
$\bar{\chi }$
are defined by
![]() $S$
and
$S$
and
![]() $F$
, respectively, then
$F$
, respectively, then
![]() $\gamma (f,p(x)) = \bar{\chi }(f,x)$
for every
$\gamma (f,p(x)) = \bar{\chi }(f,x)$
for every
![]() $x \in F$
and
$x \in F$
and
![]() $f \in \operatorname{Homeo}_0\!(M,\omega )$
. Thus
$f \in \operatorname{Homeo}_0\!(M,\omega )$
. Thus
![]() $\Gamma _{\hspace{-2px}b}$
and
$\Gamma _{\hspace{-2px}b}$
and
![]() $tr_\Gamma ^\Lambda X$
coincide. In particular,
$tr_\Gamma ^\Lambda X$
coincide. In particular,
![]() $\Gamma _{\hspace{-2px}b}$
does not depend on the choice of a measurable system of paths.
$\Gamma _{\hspace{-2px}b}$
does not depend on the choice of a measurable system of paths.
To finish the construction of
![]() $\Gamma _{\hspace{-2px}b}$
, we shall show that measurable fundamental domains exist. Suppose
$\Gamma _{\hspace{-2px}b}$
, we shall show that measurable fundamental domains exist. Suppose
![]() $\{U_i\}_{i\in \mathbb{N}}$
is a cover of
$\{U_i\}_{i\in \mathbb{N}}$
is a cover of
![]() $M$
by simply connected open sets. Let
$M$
by simply connected open sets. Let
![]() $\widetilde{U}_i$
be a homeomorphic lift of
$\widetilde{U}_i$
be a homeomorphic lift of
![]() $U_i$
to
$U_i$
to
![]() $\widetilde{M}$
. Set
$\widetilde{M}$
. Set
![]() $F_i = \widetilde{U}_i \backslash p^{-1}(\cup _{j=1}^{i-1} U_j)$
. Then
$F_i = \widetilde{U}_i \backslash p^{-1}(\cup _{j=1}^{i-1} U_j)$
. Then
![]() $F = \cup _{j=1}^\infty F_j$
is a strict measurable fundamental domain.
$F = \cup _{j=1}^\infty F_j$
is a strict measurable fundamental domain.
3.3. Description of
 $\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
$\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
We describe an extension of
![]() $\Gamma _b$
to a map that ranges in the bounded cohomology of
$\Gamma _b$
to a map that ranges in the bounded cohomology of
![]() $\operatorname{Homeo}\!(M,\omega )$
. It is done by modifying the notion of a system of paths. In this and the next subsection, we assume that
$\operatorname{Homeo}\!(M,\omega )$
. It is done by modifying the notion of a system of paths. In this and the next subsection, we assume that
![]() $M$
is compact.
$M$
is compact.
Fix a point
![]() $* \in M$
. Let
$* \in M$
. Let
![]() $\operatorname{Homeo}(M,*)$
be the group of homeomorphisms of
$\operatorname{Homeo}(M,*)$
be the group of homeomorphisms of
![]() $M$
fixing
$M$
fixing
![]() $*$
and
$*$
and
![]() $\operatorname{Homeo}_0(M,*)$
the subgroup of homeomorphisms that are isotopic to the identity by
$\operatorname{Homeo}_0(M,*)$
the subgroup of homeomorphisms that are isotopic to the identity by
![]() $*$
-fixing homeomorphisms. It follows from [Reference Edwards and Kirby8, Corollary 1.1], which for compact
$*$
-fixing homeomorphisms. It follows from [Reference Edwards and Kirby8, Corollary 1.1], which for compact
![]() $M$
,
$M$
,
![]() $\operatorname{Homeo}_0(M,*)$
is the connected component of the identity in
$\operatorname{Homeo}_0(M,*)$
is the connected component of the identity in
![]() $\operatorname{Homeo}(M,*)$
equipped with the compact-open topology. Recall that in these groups, we compose homeomorphisms from left to right. Consider the mapping class group
$\operatorname{Homeo}(M,*)$
equipped with the compact-open topology. Recall that in these groups, we compose homeomorphisms from left to right. Consider the mapping class group
Let
![]() $\operatorname{Homeo}(M,*\to x) \lt \operatorname{Homeo}(M)$
be the subset of homeomorphisms of
$\operatorname{Homeo}(M,*\to x) \lt \operatorname{Homeo}(M)$
be the subset of homeomorphisms of
![]() $M$
that send
$M$
that send
![]() $*$
to
$*$
to
![]() $x$
. Suppose
$x$
. Suppose
![]() $h_x \in \operatorname{Homeo}(M,*\to x)$
. Denote by
$h_x \in \operatorname{Homeo}(M,*\to x)$
. Denote by
![]() $[h_x]$
the connected component of
$[h_x]$
the connected component of
![]() $h_x$
in
$h_x$
in
![]() $\operatorname{Homeo}(M,*\to x)$
with the compact-open topology. Note that two elements
$\operatorname{Homeo}(M,*\to x)$
with the compact-open topology. Note that two elements
![]() $h_x$
and
$h_x$
and
![]() $g_x$
in
$g_x$
in
![]() $\operatorname{Homeo}(M,*\to x)$
are in the same connected component if and only if there exists an isotopy
$\operatorname{Homeo}(M,*\to x)$
are in the same connected component if and only if there exists an isotopy
![]() $f_t$
connecting
$f_t$
connecting
![]() $h_x$
to
$h_x$
to
![]() $g_x$
such that
$g_x$
such that
![]() $f_t(*) = x$
for all
$f_t(*) = x$
for all
![]() $t$
. A system of homeomorphisms for
$t$
. A system of homeomorphisms for
![]() $M$
is a function on
$M$
is a function on
![]() $M$
of the form
$M$
of the form
![]() $P(x) = [h_x]$
, where
$P(x) = [h_x]$
, where
![]() $h_x \in \operatorname{Homeo}(M,*\to x)$
. For example, it can be a point-pushing map along
$h_x \in \operatorname{Homeo}(M,*\to x)$
. For example, it can be a point-pushing map along
![]() $s_x$
, where
$s_x$
, where
![]() $S(x) = [s_x]$
is a system of paths.
$S(x) = [s_x]$
is a system of paths.
Let
![]() $P(x) = [h_x]$
be a system of homeomorphisms. For every
$P(x) = [h_x]$
be a system of homeomorphisms. For every
![]() $f \in \operatorname{Homeo}\!(M,\omega )$
, we have
$f \in \operatorname{Homeo}\!(M,\omega )$
, we have
![]() $h_x \circ f \circ h_{f(x)}^{-1} \in \operatorname{Homeo}(M,*)$
. We define a cocycle
$h_x \circ f \circ h_{f(x)}^{-1} \in \operatorname{Homeo}(M,*)$
. We define a cocycle
by
![]() $\gamma ^{\scriptscriptstyle \mathcal{M}}(f,x) = [h_x \circ f \circ h_{f(x)}^{-1}]$
. Note that
$\gamma ^{\scriptscriptstyle \mathcal{M}}(f,x) = [h_x \circ f \circ h_{f(x)}^{-1}]$
. Note that
![]() $\gamma ^{\scriptscriptstyle \mathcal{M}}$
does not depend on the homeomorphisms
$\gamma ^{\scriptscriptstyle \mathcal{M}}$
does not depend on the homeomorphisms
![]() $h_x$
representing
$h_x$
representing
![]() $P(x)$
but depends on the choice of
$P(x)$
but depends on the choice of
![]() $P$
. There is a notion of a measurable system of homeomorphisms, we discuss it in Section 3.4.
$P$
. There is a notion of a measurable system of homeomorphisms, we discuss it in Section 3.4.
Likewise in Section 3.1, any measurable system of homeomorphisms
![]() $P$
induces a map
$P$
induces a map
In Section 3.4, we show that
![]() $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
does not depend on the choice of
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
does not depend on the choice of
![]() $P$
. Note that
$P$
. Note that
![]() $\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
generalizes the homomorphism
$\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
generalizes the homomorphism
![]() $\mathcal{G}_{S,1}$
from [Reference Brandenbursky and Marcinkowski4] defined only for surfaces
$\mathcal{G}_{S,1}$
from [Reference Brandenbursky and Marcinkowski4] defined only for surfaces
![]() $S$
and ranging in quasimorphisms on
$S$
and ranging in quasimorphisms on
![]() $\operatorname{Homeo}(S,\omega )$
.
$\operatorname{Homeo}(S,\omega )$
.
Remark 3.3.
If
![]() $M$
is oriented, we can consider the oriented version of
$M$
is oriented, we can consider the oriented version of
![]() $\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
. Namely, let
$\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
. Namely, let
![]() $\mathcal{M}_+(M,*)$
be the subgroup of
$\mathcal{M}_+(M,*)$
be the subgroup of
![]() $\mathcal{M}(M,*)$
of mapping classes represented by orientation preserving homeomorphisms, and let
$\mathcal{M}(M,*)$
of mapping classes represented by orientation preserving homeomorphisms, and let
![]() $\operatorname{Homeo}_+\!(M,\omega )$
be homeomorphisms preserving
$\operatorname{Homeo}_+\!(M,\omega )$
be homeomorphisms preserving
![]() $\omega$
and the orientation. Assuming that for every
$\omega$
and the orientation. Assuming that for every
![]() $x\in M$
,
$x\in M$
,
![]() $P(x)$
is represented by an orientation preserving homeomorphism, we have
$P(x)$
is represented by an orientation preserving homeomorphism, we have
![]() $\gamma ^{\scriptscriptstyle \mathcal{M}}(f,x) \in \mathcal{M}_+(M,*)$
for
$\gamma ^{\scriptscriptstyle \mathcal{M}}(f,x) \in \mathcal{M}_+(M,*)$
for
![]() $f \in \operatorname{Homeo}_+\!(M,\omega )$
. Thus we can define
$f \in \operatorname{Homeo}_+\!(M,\omega )$
. Thus we can define
This map is used in Theorem 1.2 .
Let us now explain in what sense
![]() $\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
extends
$\Gamma _b^{\scriptscriptstyle \mathcal{M}}$
extends
![]() $\Gamma _b$
. Note that
$\Gamma _b$
. Note that
![]() $\mathcal{M}(M,*) = \pi _0(\operatorname{Homeo}(M,*))$
and
$\mathcal{M}(M,*) = \pi _0(\operatorname{Homeo}(M,*))$
and
![]() $\mathcal{M}(M) = \pi _0(\operatorname{Homeo}(M))$
. Consider the fiber bundle
$\mathcal{M}(M) = \pi _0(\operatorname{Homeo}(M))$
. Consider the fiber bundle
where
![]() $ev(f) = f(*)$
. The long exact sequence of the homotopy groups gives
$ev(f) = f(*)$
. The long exact sequence of the homotopy groups gives
For
![]() $g \in \pi _1(M,*)$
,
$g \in \pi _1(M,*)$
,
![]() $Pu(g)$
is the mapping class represented by the time-one map
$Pu(g)$
is the mapping class represented by the time-one map
![]() $f_1$
of a point-pushing isotopy
$f_1$
of a point-pushing isotopy
![]() $\{f_t\}_{t\in [0,1]}$
along a loop representing
$\{f_t\}_{t\in [0,1]}$
along a loop representing
![]() $g$
. By [Reference Brandenbursky and Marcinkowski5, Proposition 3.1],
$g$
. By [Reference Brandenbursky and Marcinkowski5, Proposition 3.1],
![]() $im(ev_1)$
lies in the center of
$im(ev_1)$
lies in the center of
![]() $\pi _1(M,*)$
; therefore,
$\pi _1(M,*)$
; therefore,
![]() $ev_1$
is trivial and
$ev_1$
is trivial and
![]() $Pu$
is an embedding.
$Pu$
is an embedding.
Let
![]() $[f] \in im(Pu) = ker(F) \lt \mathcal{M}(M,*)$
, and let
$[f] \in im(Pu) = ker(F) \lt \mathcal{M}(M,*)$
, and let
![]() $f_t$
be an isotopy connecting the identity to
$f_t$
be an isotopy connecting the identity to
![]() $f$
in
$f$
in
![]() $\operatorname{Homeo}_0(M)$
. Let
$\operatorname{Homeo}_0(M)$
. Let
![]() $Tr([f])$
be the element of
$Tr([f])$
be the element of
![]() $\pi _1(M,*)$
represented by
$\pi _1(M,*)$
represented by
![]() $f_t(*)$
. By the triviality of
$f_t(*)$
. By the triviality of
![]() $ev_1$
, this map is well defined, and it is the inverse of
$ev_1$
, this map is well defined, and it is the inverse of
![]() $Pu$
on
$Pu$
on
![]() $im(Pu)$
.
$im(Pu)$
.
Let
![]() $S$
be any measurable system of paths and
$S$
be any measurable system of paths and
![]() $P$
a system of homeomorphims such that
$P$
a system of homeomorphims such that
![]() $P(x) = [h_x]$
with
$P(x) = [h_x]$
with
![]() $h_x$
the point-pushing map along a path
$h_x$
the point-pushing map along a path
![]() $s_x$
such that
$s_x$
such that
![]() $S(x) = [s_x]$
. The cocycles
$S(x) = [s_x]$
. The cocycles
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma ^{\scriptscriptstyle \mathcal{M}}$
are defined with respect to these systems. For every
$\gamma ^{\scriptscriptstyle \mathcal{M}}$
are defined with respect to these systems. For every
![]() $f \in \operatorname{Homeo}_0\!(M,\omega )$
, we have
$f \in \operatorname{Homeo}_0\!(M,\omega )$
, we have
![]() $\gamma (f,x) = Tr(\gamma ^{\scriptscriptstyle \mathcal{M}}(f,x))$
. Thus
$\gamma (f,x) = Tr(\gamma ^{\scriptscriptstyle \mathcal{M}}(f,x))$
. Thus
![]() $Pu(\gamma (f,x)) = \gamma ^{\scriptscriptstyle \mathcal{M}}(f,x)$
, and we have a commutative diagram:
$Pu(\gamma (f,x)) = \gamma ^{\scriptscriptstyle \mathcal{M}}(f,x)$
, and we have a commutative diagram:

Thus the following diagram commute:

3.4.
 $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
via couplings
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
via couplings
We shall construct a cover of
![]() $M$
on which
$M$
on which
![]() $\mathcal{M}(M,*)$
acts on the left and
$\mathcal{M}(M,*)$
acts on the left and
![]() $\operatorname{Homeo}\!(M,\omega )$
acts on the right.
$\operatorname{Homeo}\!(M,\omega )$
acts on the right.
Recall that
![]() $ev\ :\ \operatorname{Homeo}(M) \to M$
is a fiber bundle defined by
$ev\ :\ \operatorname{Homeo}(M) \to M$
is a fiber bundle defined by
![]() $ev(f) = f(*)$
. Note that
$ev(f) = f(*)$
. Note that
![]() $\operatorname{Homeo}(M,* \to x) = ev^{-1}(x)$
. Denote by
$\operatorname{Homeo}(M,* \to x) = ev^{-1}(x)$
. Denote by
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
the set of connected components of the fibers of
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
the set of connected components of the fibers of
![]() $ev$
and by
$ev$
and by
![]() $q\ :\ \operatorname{Homeo}(M) \to \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
the quotient map. On
$q\ :\ \operatorname{Homeo}(M) \to \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
the quotient map. On
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
, we consider the quotient topology. Note that we have
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
, we consider the quotient topology. Note that we have
![]() $q(f) = q(g)$
if and only if
$q(f) = q(g)$
if and only if
![]() $f$
can be connected to
$f$
can be connected to
![]() $g$
via an isotopy preserving
$g$
via an isotopy preserving
![]() $f(*)=g(*)$
at all times.
$f(*)=g(*)$
at all times.
The map
![]() $ev$
factors via
$ev$
factors via
![]() $q$
:
$q$
:

where
![]() $p^{\scriptscriptstyle \mathcal{M}}$
is the unique map making the above diagram commutative.
$p^{\scriptscriptstyle \mathcal{M}}$
is the unique map making the above diagram commutative.
The evaluation map is a fiber bundle; thus, every
![]() $x \in M$
has an open neighborhood
$x \in M$
has an open neighborhood
![]() $U$
such that
$U$
such that
![]() $ev^{-1}(U)$
is homeomorphic to
$ev^{-1}(U)$
is homeomorphic to
![]() $ U \times \operatorname{Homeo}(M,*)$
by a fiber preserving homeomorphism. Moreover, by the definition of
$ U \times \operatorname{Homeo}(M,*)$
by a fiber preserving homeomorphism. Moreover, by the definition of
![]() $q$
, we have that
$q$
, we have that
![]() $q(ev^{-1}(U))$
is the disjoint union of copies of
$q(ev^{-1}(U))$
is the disjoint union of copies of
![]() $U$
. On each such a copy,
$U$
. On each such a copy,
![]() $p^{\scriptscriptstyle \mathcal{M}}$
is a homeomorphism. Thus,
$p^{\scriptscriptstyle \mathcal{M}}$
is a homeomorphism. Thus,
![]() $p^{\scriptscriptstyle \mathcal{M}}$
is a covering map.
$p^{\scriptscriptstyle \mathcal{M}}$
is a covering map.
Denote by
![]() $\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
the measure on
$\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
the measure on
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
defined by the pullback of the volume form on
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
defined by the pullback of the volume form on
![]() $M$
that defines
$M$
that defines
![]() $\omega$
. We shall define the mentioned left and right actions.
$\omega$
. We shall define the mentioned left and right actions.
Let
![]() $[c] \in \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
be a connected component of
$[c] \in \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
be a connected component of
![]() $ev^{-1}(c(*))$
represented by
$ev^{-1}(c(*))$
represented by
![]() $c \in \operatorname{Homeo}(M)$
and
$c \in \operatorname{Homeo}(M)$
and
![]() $[h] \in \mathcal{M}(M,*)$
be a mapping class represented by
$[h] \in \mathcal{M}(M,*)$
be a mapping class represented by
![]() $h \in \operatorname{Homeo}(M,*)$
. The left action of
$h \in \operatorname{Homeo}(M,*)$
. The left action of
![]() $\mathcal{M}(M,*)$
on
$\mathcal{M}(M,*)$
on
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
is given by
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
is given by
![]() $[h].[c] = [hc] \in \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
(note that we compose homeomorphisms starting from the left), where
$[h].[c] = [hc] \in \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
(note that we compose homeomorphisms starting from the left), where
![]() $[hc]$
denotes the connected component of
$[hc]$
denotes the connected component of
![]() $ev^{-1}(c(*))$
containing
$ev^{-1}(c(*))$
containing
![]() $hc$
. This action is transitive on the fibers of
$hc$
. This action is transitive on the fibers of
![]() $p^{\scriptscriptstyle \mathcal{M}}$
and permutes the components of
$p^{\scriptscriptstyle \mathcal{M}}$
and permutes the components of
![]() $q(ev^{-1}(U))$
, where
$q(ev^{-1}(U))$
, where
![]() $U$
is as above. Therefore, it is a deck-transformation group of
$U$
is as above. Therefore, it is a deck-transformation group of
![]() $ \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
and preserves
$ \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
and preserves
![]() $\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
.
$\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
.
Let
![]() $[c] \in \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
and
$[c] \in \widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
and
![]() $f \in \operatorname{Homeo}\!(M,\omega )$
. The right action of
$f \in \operatorname{Homeo}\!(M,\omega )$
. The right action of
![]() $\operatorname{Homeo}\!(M,\omega )$
on
$\operatorname{Homeo}\!(M,\omega )$
on
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
is given by
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
is given by
![]() $[c].f = [cf]$
, where
$[c].f = [cf]$
, where
![]() $[cf]$
is the connected component of
$[cf]$
is the connected component of
![]() $ev^{-1}(f(c(*))$
containing
$ev^{-1}(f(c(*))$
containing
![]() $cf$
. This action covers the
$cf$
. This action covers the
![]() $\operatorname{Homeo}\!(M,\omega )$
-action on
$\operatorname{Homeo}\!(M,\omega )$
-action on
![]() $M$
and thus is
$M$
and thus is
![]() $\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
-preserving.
$\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
-preserving.
The above actions define a coupling on
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
. Moreover, by construction, if
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
. Moreover, by construction, if
![]() $P$
is a system of homeomorphisms,
$P$
is a system of homeomorphisms,
![]() $im(P)$
is a subset of
$im(P)$
is a subset of
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
. We say that a system of homeomorphisms
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
. We say that a system of homeomorphisms
![]() $P$
is measurable if
$P$
is measurable if
![]() $im(P)$
is
$im(P)$
is
![]() $\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
-measurable.
$\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
-measurable.
Every measurable system of homeomorphisms defines a strict fundamental domain for the
![]() $\mathcal{M}(M,*)$
-action and vice versa. It follows directly from definitions (see Section 3.2) that the constructions described in Section 3.3 and [Reference Nitsche19] coincide. In particular,
$\mathcal{M}(M,*)$
-action and vice versa. It follows directly from definitions (see Section 3.2) that the constructions described in Section 3.3 and [Reference Nitsche19] coincide. In particular,
![]() $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
does not depend on the choice of a measurable system of paths [Reference Nitsche19, Lemma 3.3].
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
does not depend on the choice of a measurable system of paths [Reference Nitsche19, Lemma 3.3].
Note that
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
is disconnected and contains the universal cover of
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
is disconnected and contains the universal cover of
![]() $M$
. Indeed, let
$M$
. Indeed, let
![]() $\widetilde{M}_0$
be the subset of
$\widetilde{M}_0$
be the subset of
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
containing classes that are represented by homeomorphisms isotopic to the identity in
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
containing classes that are represented by homeomorphisms isotopic to the identity in
![]() $\operatorname{Homeo}(M)$
. The subgroup
$\operatorname{Homeo}(M)$
. The subgroup
![]() $\pi _1(M,*) \lt \mathcal{M}(M,*)$
acts on
$\pi _1(M,*) \lt \mathcal{M}(M,*)$
acts on
![]() $\widetilde{M}_0$
, and the quotient is
$\widetilde{M}_0$
, and the quotient is
![]() $M$
; thus,
$M$
; thus,
![]() $\widetilde{M}_0$
is the universal cover of
$\widetilde{M}_0$
is the universal cover of
![]() $M$
. An explicit isomorphism between
$M$
. An explicit isomorphism between
![]() $\widetilde{M}_0$
and
$\widetilde{M}_0$
and
![]() $\widetilde{M}$
is given by the map
$\widetilde{M}$
is given by the map
![]() $T\ :\ \widetilde{M}_0 \to \widetilde{M}$
, where
$T\ :\ \widetilde{M}_0 \to \widetilde{M}$
, where
![]() $T([c])$
is the homotopy class of the path
$T([c])$
is the homotopy class of the path
![]() $c_t(*)$
traced by any isotopy
$c_t(*)$
traced by any isotopy
![]() $c_t$
connecting
$c_t$
connecting
![]() $Id_M$
to
$Id_M$
to
![]() $c$
. By the triviality of
$c$
. By the triviality of
![]() $ev_1\ :\ \pi _1(\operatorname{Homeo}(M)) \to \pi _1(M,*)$
, this map is well defined. Therefore,
$ev_1\ :\ \pi _1(\operatorname{Homeo}(M)) \to \pi _1(M,*)$
, this map is well defined. Therefore,
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
consists of infinitely many copies of
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
consists of infinitely many copies of
![]() $\widetilde{M}$
indexed by the right cosets of
$\widetilde{M}$
indexed by the right cosets of
![]() $\pi _1(M,*)$
in
$\pi _1(M,*)$
in
![]() $\mathcal{M}(M,*)$
.
$\mathcal{M}(M,*)$
.
Finally, we show that measurable systems of homeomorphisms exist. It follows from the existence of measurable systems of paths. Let
![]() $S(x) = [s_x]$
be a measurable system of paths, and let
$S(x) = [s_x]$
be a measurable system of paths, and let
![]() $P(x) = [h_x]$
, where
$P(x) = [h_x]$
, where
![]() $h_x$
is a point-pushing map along
$h_x$
is a point-pushing map along
![]() $s_x$
. Using the isomorphism
$s_x$
. Using the isomorphism
![]() $T\ :\ \widetilde{M}_0 \to \widetilde{M}$
, we can regard
$T\ :\ \widetilde{M}_0 \to \widetilde{M}$
, we can regard
![]() $im(S)$
as a
$im(S)$
as a
![]() $\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
-measurable subset of
$\widetilde{\omega }^{\scriptscriptstyle \mathcal{M}}$
-measurable subset of
![]() $\widetilde{M}_0$
, and under this identification
$\widetilde{M}_0$
, and under this identification
![]() $im(S) = im(P)$
. Thus
$im(S) = im(P)$
. Thus
![]() $P$
is a measurable system of homeomorphisms.
$P$
is a measurable system of homeomorphisms.
Remark 3.4.
Set
![]() $\pi = \pi _1(M,*)$
. The cover
$\pi = \pi _1(M,*)$
. The cover
![]() $\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
is isomorphic to
$\widetilde{M}^{\scriptscriptstyle \mathcal{M}}$
is isomorphic to
![]() $(\mathcal{M}(M,*) \times \widetilde{M})/_\pi$
, where
$(\mathcal{M}(M,*) \times \widetilde{M})/_\pi$
, where
![]() $\pi$
acts on
$\pi$
acts on
![]() $\mathcal{M}(M,*) \times \widetilde{M}$
by
$\mathcal{M}(M,*) \times \widetilde{M}$
by
![]() $\gamma .(h,x) = (h\gamma ^{-1},\gamma .x)$
.
$\gamma .(h,x) = (h\gamma ^{-1},\gamma .x)$
.
4. Restriction to a free subgroup
In this section, we find a free subgroup
![]() $F$
of
$F$
of
![]() $\pi _1(M,*)$
such that volume and Euler classes restricted to
$\pi _1(M,*)$
such that volume and Euler classes restricted to
![]() $F$
have positive norms.
$F$
have positive norms.
4.1. Volume class in dimension 2
Let
![]() $X$
be a topological space. The
$X$
be a topological space. The
![]() $l^1$
-homology of
$l^1$
-homology of
![]() $X$
is denoted by
$X$
is denoted by
![]() $\operatorname{H}^{l_1}_n(X)$
[Reference Frigerio9, Chapter 6]. In
$\operatorname{H}^{l_1}_n(X)$
[Reference Frigerio9, Chapter 6]. In
![]() $l^1$
-homology, we allow chains to be infinite sums
$l^1$
-homology, we allow chains to be infinite sums
![]() $c = \Sigma _i^\infty a_i\sigma _i$
, where
$c = \Sigma _i^\infty a_i\sigma _i$
, where
![]() $|\hspace{-1px}| c |\hspace{-1px}| = \Sigma _i^\infty |a_i| \lt \infty$
. As usual, the norm on chains induces the norm on
$|\hspace{-1px}| c |\hspace{-1px}| = \Sigma _i^\infty |a_i| \lt \infty$
. As usual, the norm on chains induces the norm on
![]() $\operatorname{H}^{l_1}_n(X)$
. We have a Kronecker product between
$\operatorname{H}^{l_1}_n(X)$
. We have a Kronecker product between
![]() $l^1$
-homology and bounded cohomology:
$l^1$
-homology and bounded cohomology:
The Kronecker product is defined on the level of chains by
![]() $\langle b, a \rangle = \Sigma _i^\infty a_ib(\sigma _i)$
, where
$\langle b, a \rangle = \Sigma _i^\infty a_ib(\sigma _i)$
, where
![]() $a = \Sigma _i^\infty a_i\sigma _i$
and
$a = \Sigma _i^\infty a_i\sigma _i$
and
![]() $b$
is a bounded cochain. Moreover, we have
$b$
is a bounded cochain. Moreover, we have
![]() $| \langle B, A \rangle | \leq |\hspace{-1px}| B |\hspace{-1px}| |\hspace{-1px}| A |\hspace{-1px}|$
, where
$| \langle B, A \rangle | \leq |\hspace{-1px}| B |\hspace{-1px}| |\hspace{-1px}| A |\hspace{-1px}|$
, where
![]() $B \in \operatorname{H}_b^n(X)$
and
$B \in \operatorname{H}_b^n(X)$
and
![]() $A \in \operatorname{H}_n^{l_1}(X)$
. The following lemma is a variation of a result obtained in [Reference Mitsumatsu16]. We do not assume that
$A \in \operatorname{H}_n^{l_1}(X)$
. The following lemma is a variation of a result obtained in [Reference Mitsumatsu16]. We do not assume that
![]() $S$
is closed.
$S$
is closed.
Lemma 4.1.
Let
![]() $S$
be an oriented hyperbolic surface with non-abelian fundamental group. Then
$S$
be an oriented hyperbolic surface with non-abelian fundamental group. Then
![]() $Vol_S$
has a positive norm.
$Vol_S$
has a positive norm.
Proof. We shall find
![]() $C\in \operatorname{H}_2^{l_1}(S)$
such that
$C\in \operatorname{H}_2^{l_1}(S)$
such that
![]() $\langle Vol_S, C\rangle \neq 0$
. We can assume that
$\langle Vol_S, C\rangle \neq 0$
. We can assume that
![]() $S$
is a quotient of
$S$
is a quotient of
![]() $\mathbb{H}^2$
, as in the beginning of the proof of Lemma 2.2. Let
$\mathbb{H}^2$
, as in the beginning of the proof of Lemma 2.2. Let
![]() $p\ :\ \mathbb{H}^2\to S$
be the covering map, and let
$p\ :\ \mathbb{H}^2\to S$
be the covering map, and let
![]() $G = \pi _1(S)$
. Since
$G = \pi _1(S)$
. Since
![]() $G$
is a surface group or is free, the commutator subgroup
$G$
is a surface group or is free, the commutator subgroup
![]() $[G,G]$
is non-abelian and hence contains a hyperbolic element
$[G,G]$
is non-abelian and hence contains a hyperbolic element
![]() $\gamma \in [G,G]$
[Reference Katok14, Theorem 2.4.4]. Let
$\gamma \in [G,G]$
[Reference Katok14, Theorem 2.4.4]. Let
![]() $A_\gamma \subset \mathbb{H}^2$
be the axis of
$A_\gamma \subset \mathbb{H}^2$
be the axis of
![]() $\gamma$
. The conjugacy class of
$\gamma$
. The conjugacy class of
![]() $\gamma$
is represented by the closed geodesic
$\gamma$
is represented by the closed geodesic
![]() $L_\gamma = p(A_\gamma )\subset S$
. We regard
$L_\gamma = p(A_\gamma )\subset S$
. We regard
![]() $L_\gamma$
as a map from
$L_\gamma$
as a map from
![]() $[0,1]$
to
$[0,1]$
to
![]() $S$
. Since
$S$
. Since
![]() $\gamma \in [G,G]$
,
$\gamma \in [G,G]$
,
![]() $\gamma$
is homologically trivial. Hence there exists a triangulated subsurface
$\gamma$
is homologically trivial. Hence there exists a triangulated subsurface
![]() $S_0 \subset S$
such that
$S_0 \subset S$
such that
![]() $\partial S_0 = L_\gamma$
.
$\partial S_0 = L_\gamma$
.
The loop
![]() $L_\gamma$
is the boundary of an
$L_\gamma$
is the boundary of an
![]() $l^1$
-chain
$l^1$
-chain
![]() $c_0$
whose simplices are contained in the image of
$c_0$
whose simplices are contained in the image of
![]() $L_\gamma$
[Reference Mitsumatsu16, Section 3]. Thus
$L_\gamma$
[Reference Mitsumatsu16, Section 3]. Thus
![]() $c = S_0-c_0$
is an
$c = S_0-c_0$
is an
![]() $l^1$
-cycle. Recall that
$l^1$
-cycle. Recall that
![]() $Vol_S = [v^{\prime }_S]$
. The straightening of every simplex in
$Vol_S = [v^{\prime }_S]$
. The straightening of every simplex in
![]() $c_0$
is degenerate (
$c_0$
is degenerate (
![]() $L_\gamma$
is a geodesic); thus, we have
$L_\gamma$
is a geodesic); thus, we have
![]() $\langle v^{\prime }_S, c_0 \rangle = 0$
. We can assume that the triangulation of
$\langle v^{\prime }_S, c_0 \rangle = 0$
. We can assume that the triangulation of
![]() $S_0$
consists of geodesic simplices; hence
$S_0$
consists of geodesic simplices; hence
![]() $\langle v^{\prime }_S, S_0\rangle$
equals the hyperbolic volume of
$\langle v^{\prime }_S, S_0\rangle$
equals the hyperbolic volume of
![]() $S_0$
. Hence if we set
$S_0$
. Hence if we set
![]() $C\; =\; [c]$
, we obtain
$C\; =\; [c]$
, we obtain
![]() $\langle Vol_S, C \rangle \gt 0$
. The inequality
$\langle Vol_S, C \rangle \gt 0$
. The inequality
![]() $\langle Vol_S, C \rangle \leq |\hspace{-1px}| Vol_S |\hspace{-1px}| |\hspace{-1px}| C |\hspace{-1px}|$
implies that the norm of
$\langle Vol_S, C \rangle \leq |\hspace{-1px}| Vol_S |\hspace{-1px}| |\hspace{-1px}| C |\hspace{-1px}|$
implies that the norm of
![]() $Vol_S$
is positive.
$Vol_S$
is positive.
The following corollary is stated in the group version terms of the volume class.
Corollary 4.2.
Let
![]() $S$
be an oriented hyperbolic surface with non-abelian fundamental group. There exists an embedding
$S$
be an oriented hyperbolic surface with non-abelian fundamental group. There exists an embedding
![]() $i\ :\ F \to \pi _1(S)$
of a free non-abelian group
$i\ :\ F \to \pi _1(S)$
of a free non-abelian group
![]() $F$
such that
$F$
such that
![]() $i^*(Vol_S^{gp})$
has a positive norm.
$i^*(Vol_S^{gp})$
has a positive norm.
Proof. Let
![]() $F$
be any free non-abelian subgroup of
$F$
be any free non-abelian subgroup of
![]() $S$
(which can be equal to
$S$
(which can be equal to
![]() $\pi _1(S)$
if
$\pi _1(S)$
if
![]() $S$
is not closed). We have
$S$
is not closed). We have
![]() $i^*(Vol_S^{gp}) = Vol_{i(F)}$
. By Lemma 2.2, we know that the norm of
$i^*(Vol_S^{gp}) = Vol_{i(F)}$
. By Lemma 2.2, we know that the norm of
![]() $Vol_{i(F)}$
is equal to the norm of
$Vol_{i(F)}$
is equal to the norm of
![]() $Vol_{S^{\prime }}$
, where
$Vol_{S^{\prime }}$
, where
![]() $S^{\prime } = \mathbb{H}^2/i(F)$
, and by Lemma 4.1, the norm of
$S^{\prime } = \mathbb{H}^2/i(F)$
, and by Lemma 4.1, the norm of
![]() $Vol_{S^{\prime }}$
is positive.
$Vol_{S^{\prime }}$
is positive.
4.2. Volume class in dimension 3
For some Kleinian groups, that is, the discrete subgroups of
![]() $Iso_+(\mathbb{H}^3)$
, the volume class was studied in [Reference Soma20]. Note that if
$Iso_+(\mathbb{H}^3)$
, the volume class was studied in [Reference Soma20]. Note that if
![]() $G$
is a torsion-free Kleinian group, then it acts freely and properly discontinuously on
$G$
is a torsion-free Kleinian group, then it acts freely and properly discontinuously on
![]() $\mathbb{H}^3$
. Thus
$\mathbb{H}^3$
. Thus
![]() $\mathbb{H}^3/G$
is a manifold.
$\mathbb{H}^3/G$
is a manifold.
Theorem 4.3.
[
Reference Soma20, Theorem 1] Let
![]() $G \lt Iso_+(\mathbb{H}^3)$
be a torsion-free topologically tame Kleinian group such that the volume of
$G \lt Iso_+(\mathbb{H}^3)$
be a torsion-free topologically tame Kleinian group such that the volume of
![]() $M = \mathbb{H}^3/G$
is infinite. Then
$M = \mathbb{H}^3/G$
is infinite. Then
![]() $Vol_M$
has a positive norm if and only if
$Vol_M$
has a positive norm if and only if
![]() $G$
is not elementary and geometrically infinite.
$G$
is not elementary and geometrically infinite.
A Kleinian group
![]() $G$
is geometrically finite if
$G$
is geometrically finite if
![]() $N_\epsilon (H(L_G)/G)$
has finite volume for some
$N_\epsilon (H(L_G)/G)$
has finite volume for some
![]() $\epsilon \gt 0$
, where
$\epsilon \gt 0$
, where
![]() $N_\epsilon$
is an
$N_\epsilon$
is an
![]() $\epsilon$
neighborhood and
$\epsilon$
neighborhood and
![]() $H(L_G)$
is the convex closure of the limit set of
$H(L_G)$
is the convex closure of the limit set of
![]() $G$
[Reference Thurston21, Chapter 8, Definition 8.4.1]. A torsion-free Kleinian group
$G$
[Reference Thurston21, Chapter 8, Definition 8.4.1]. A torsion-free Kleinian group
![]() $G$
is topologically tame if
$G$
is topologically tame if
![]() $\mathbb{H}^3/G$
is homeomorphic to the interior of a compact manifold.
$\mathbb{H}^3/G$
is homeomorphic to the interior of a compact manifold.
Note that every discrete finitely generated non-abelian free subgroup
![]() $F$
of
$F$
of
![]() $Iso_+(\mathbb{H}^3)$
is topologically tame [Reference Agol1, Reference Calegari and Gabai6], not elementary and
$Iso_+(\mathbb{H}^3)$
is topologically tame [Reference Agol1, Reference Calegari and Gabai6], not elementary and
![]() $\mathbb{H}^3/F$
has infinite volume (otherwise, by the thick-thin decomposition,
$\mathbb{H}^3/F$
has infinite volume (otherwise, by the thick-thin decomposition,
![]() $\mathbb{H}^3/F$
would have a cusp and
$\mathbb{H}^3/F$
would have a cusp and
![]() $\mathbb{Z}^2$
would embed in
$\mathbb{Z}^2$
would embed in
![]() $F$
). Let
$F$
). Let
![]() $M$
be an oriented
$M$
be an oriented
![]() $3$
-dimensional hyperbolic manifold. Then for every free group
$3$
-dimensional hyperbolic manifold. Then for every free group
![]() $F$
in
$F$
in
![]() $\pi _1(M) \lt Iso_+(\mathbb{H}^3)$
which is geometrically infinite,
$\pi _1(M) \lt Iso_+(\mathbb{H}^3)$
which is geometrically infinite,
![]() $Vol_F$
has positive norm. Below we describe our main example of such a situation, that is, manifolds that fiber over the circle with non-compact fiber.
$Vol_F$
has positive norm. Below we describe our main example of such a situation, that is, manifolds that fiber over the circle with non-compact fiber.
Example 4.4.
Suppose
![]() $S$
is a connected oriented surface without boundary and free fundamental group
$S$
is a connected oriented surface without boundary and free fundamental group
![]() $F = \pi _1(S)$
. Let
$F = \pi _1(S)$
. Let
![]() $f \in \operatorname{Diff}^{+}(S)$
. The mapping torus of
$f \in \operatorname{Diff}^{+}(S)$
. The mapping torus of
![]() $f$
is a
$f$
is a
![]() $3$
-dimensional manifold
$3$
-dimensional manifold
![]() $M_f = S \times [0,1] / \sim$
, where
$M_f = S \times [0,1] / \sim$
, where
![]() $(x,0) \sim (f(x),1)$
. That is, the boundary components of
$(x,0) \sim (f(x),1)$
. That is, the boundary components of
![]() $S \times [0,1]$
are glued together via
$S \times [0,1]$
are glued together via
![]() $f$
. Note that
$f$
. Note that
![]() $M_f$
fibers over the circle with fiber
$M_f$
fibers over the circle with fiber
![]() $S$
, and conversely, every
$S$
, and conversely, every
![]() $3$
-manifold that fibers over a circle with fiber
$3$
-manifold that fibers over a circle with fiber
![]() $S$
can be constructed in this way. The mapping torus
$S$
can be constructed in this way. The mapping torus
![]() $M_f$
is hyperbolic if and only if
$M_f$
is hyperbolic if and only if
![]() $f$
is isotopic to a pseudo-Anosov map [Reference Thurston22]. If
$f$
is isotopic to a pseudo-Anosov map [Reference Thurston22]. If
![]() $M_f$
is hyperbolic, the hyperbolic structure is unique, and we have a unique class
$M_f$
is hyperbolic, the hyperbolic structure is unique, and we have a unique class
![]() $Vol^{gp}_{M_f} \in \operatorname{H}_b^3(\pi _1(M_f))$
. Now the inclusion of the fiber
$Vol^{gp}_{M_f} \in \operatorname{H}_b^3(\pi _1(M_f))$
. Now the inclusion of the fiber
![]() $S$
into
$S$
into
![]() $M_f$
gives an embedding
$M_f$
gives an embedding
![]() $i\ :\ F \to \pi _1(M_f)$
, and
$i\ :\ F \to \pi _1(M_f)$
, and
![]() $i(F)$
is a normal subgroup of
$i(F)$
is a normal subgroup of
![]() $\pi _1(M)$
. It follows that the limit set of
$\pi _1(M)$
. It follows that the limit set of
![]() $i(F)$
is equal to the limit set of
$i(F)$
is equal to the limit set of
![]() $\pi _1(M)$
[
Reference Thurston21, Chapter 8, Corollary 8.1.3]; thus, it is the entire sphere at infinity. Hence
$\pi _1(M)$
[
Reference Thurston21, Chapter 8, Corollary 8.1.3]; thus, it is the entire sphere at infinity. Hence
![]() $i(F)$
is geometrically infinite. By Theorem
4.3
, we have that
$i(F)$
is geometrically infinite. By Theorem
4.3
, we have that
![]() $i^*(Vol^{gp}_{M_f}) = Vol_{i(F)}$
has positive norm.
$i^*(Vol^{gp}_{M_f}) = Vol_{i(F)}$
has positive norm.
4.3. Euler class
We briefly recall basic definitions concerning quasimorphisms [Reference Frigerio9, Chapter 2]. Let
![]() $G$
be a group. A real function
$G$
be a group. A real function
![]() $q\ :\ G \to \mathbb{R}$
is called a quasimorphism if there exists some
$q\ :\ G \to \mathbb{R}$
is called a quasimorphism if there exists some
![]() $D \in \mathbb{R}$
such that
$D \in \mathbb{R}$
such that
for any
![]() $a,b \in G$
. The minimal such
$a,b \in G$
. The minimal such
![]() $D$
is called the defect of
$D$
is called the defect of
![]() $q$
. A quasimorphism is homogeneous if
$q$
. A quasimorphism is homogeneous if
![]() $q(a^n) = nq(a)$
for any
$q(a^n) = nq(a)$
for any
![]() $a\in G$
and
$a\in G$
and
![]() $n \in \mathbb{Z}$
. The nonhomogeneous coboundary
$n \in \mathbb{Z}$
. The nonhomogeneous coboundary
![]() $dq(a,b) = q(a)-q(ab)+q(b)$
of
$dq(a,b) = q(a)-q(ab)+q(b)$
of
![]() $q$
is interpreted as a second bounded cohomology class
$q$
is interpreted as a second bounded cohomology class
![]() $[dq] \in \operatorname{H}_b^2(G)$
. If
$[dq] \in \operatorname{H}_b^2(G)$
. If
![]() $q$
is homogeneous and not a homomorphism, then
$q$
is homogeneous and not a homomorphism, then
![]() $[dq]$
is non-trivial and has a positive norm [Reference Frigerio9, Corollary 6.7].
$[dq]$
is non-trivial and has a positive norm [Reference Frigerio9, Corollary 6.7].
Lemma 4.5.
Let
![]() $S$
be an oriented closed surface of genus
$S$
be an oriented closed surface of genus
![]() $\geq 2$
. There exists an embedding
$\geq 2$
. There exists an embedding
![]() $i\ :\ F \to \pi _1(S)$
of a free non-abelian group
$i\ :\ F \to \pi _1(S)$
of a free non-abelian group
![]() $F$
such that
$F$
such that
![]() $i^*(e_b^S)$
has a positive norm.
$i^*(e_b^S)$
has a positive norm.
Proof. Let
![]() $T^1S$
be the unit tangent bundle of
$T^1S$
be the unit tangent bundle of
![]() $S$
and denote by
$S$
and denote by
![]() $q\ :\ \pi _1(T^1S) \to \pi _1(S)$
the map induced by the projection
$q\ :\ \pi _1(T^1S) \to \pi _1(S)$
the map induced by the projection
![]() $T^1S \to S$
. We will use the rotation quasimorphism
$T^1S \to S$
. We will use the rotation quasimorphism
![]() $Rot\ :\ \pi _1(T^1S) \to \mathbb{R}$
defined in [Reference Huber12]. It is a homogeneous quasimorphism of defect
$Rot\ :\ \pi _1(T^1S) \to \mathbb{R}$
defined in [Reference Huber12]. It is a homogeneous quasimorphism of defect
![]() $1$
, which trivializes the pullback
$1$
, which trivializes the pullback
![]() $q^*(e_b^S) \in \operatorname{H}_b^2(\pi _1(T^1S))$
, that is,
$q^*(e_b^S) \in \operatorname{H}_b^2(\pi _1(T^1S))$
, that is,
![]() $q^*(e_b^S) = [d Rot]$
[Reference Huber12, Theorem 5.9].
$q^*(e_b^S) = [d Rot]$
[Reference Huber12, Theorem 5.9].
Let
![]() $a,b \in \pi _1(T^1S)$
be such that
$a,b \in \pi _1(T^1S)$
be such that
![]() $Rot(ab) \neq Rot(a)+Rot(b)$
. Let
$Rot(ab) \neq Rot(a)+Rot(b)$
. Let
![]() $F = \langle q(a),q(b) \rangle \lt \pi _1(S)$
. Denote this inclusion by
$F = \langle q(a),q(b) \rangle \lt \pi _1(S)$
. Denote this inclusion by
![]() $i\ :\ F \to \pi _1(S)$
, and set
$i\ :\ F \to \pi _1(S)$
, and set
![]() $F^{\prime } = q^{-1}(F)$
. It follows from the definition of
$F^{\prime } = q^{-1}(F)$
. It follows from the definition of
![]() $a$
and
$a$
and
![]() $b$
that
$b$
that
![]() $Rot_{|F^{\prime }}$
is a homogeneous quasimorphism that is not a homomorphism. Thus
$Rot_{|F^{\prime }}$
is a homogeneous quasimorphism that is not a homomorphism. Thus
![]() $q^*(e^S_b)_{|F^{\prime }}$
has positive norm, and
$q^*(e^S_b)_{|F^{\prime }}$
has positive norm, and
![]() $i^*(e^S_b)$
must have positive norm since
$i^*(e^S_b)$
must have positive norm since
![]() $q^*i^*(e^S_b) = q^*(e^S_b)_{|F^{\prime }}$
. Finally,
$q^*i^*(e^S_b) = q^*(e^S_b)_{|F^{\prime }}$
. Finally,
![]() $F$
must be free of rank
$F$
must be free of rank
![]() $2$
. Indeed, every subgroup of
$2$
. Indeed, every subgroup of
![]() $\pi _1(S)$
is free non-abelian, abelian, or is a surface group. But surface groups are not generated by
$\pi _1(S)$
is free non-abelian, abelian, or is a surface group. But surface groups are not generated by
![]() $2$
elements, and abelian groups do not carry a non-trivial class in their second bounded cohomology. Thus
$2$
elements, and abelian groups do not carry a non-trivial class in their second bounded cohomology. Thus
![]() $F$
is free non-abelian of rank
$F$
is free non-abelian of rank
![]() $2$
.
$2$
.
5. Proof of the theorem
Let
![]() $M$
be a manifold with a volume form
$M$
be a manifold with a volume form
![]() $\omega$
. As usual,
$\omega$
. As usual,
![]() $\omega$
denotes as well the induced measure, and we assume that this measure is finite. Suppose
$\omega$
denotes as well the induced measure, and we assume that this measure is finite. Suppose
![]() $i\ :\ F \to \pi _1(M)$
is an embedding and consider
$i\ :\ F \to \pi _1(M)$
is an embedding and consider
![]() $i^*\ :\ \operatorname{H}_b^\bullet (\pi _1(M)) \to \operatorname{H}_b^\bullet (F)$
. Let
$i^*\ :\ \operatorname{H}_b^\bullet (\pi _1(M)) \to \operatorname{H}_b^\bullet (F)$
. Let
![]() $\rho\ :\ F \to \operatorname{Homeo}_0\!(M,\omega )$
be a representation of
$\rho\ :\ F \to \operatorname{Homeo}_0\!(M,\omega )$
be a representation of
![]() $F$
by homeomorphisms. Let
$F$
by homeomorphisms. Let
![]() $\rho ^*\ :\ \operatorname{H}_b^\bullet (\operatorname{Homeo}_0\!(M,\omega )) \to \operatorname{H}_b^\bullet (F)$
. Thus we have a not necessarily commutative diagram:
$\rho ^*\ :\ \operatorname{H}_b^\bullet (\operatorname{Homeo}_0\!(M,\omega )) \to \operatorname{H}_b^\bullet (F)$
. Thus we have a not necessarily commutative diagram:

Let
![]() $\Lambda, \epsilon \in \mathbb{R}$
. We say that
$\Lambda, \epsilon \in \mathbb{R}$
. We say that
![]() $\rho$
is an
$\rho$
is an
![]() $(F, \Lambda, \epsilon )$
-inverse of
$(F, \Lambda, \epsilon )$
-inverse of
![]() $\Gamma _b$
if for every
$\Gamma _b$
if for every
![]() $C \in \operatorname{H}_b^\bullet (\pi _1(M))$
, we have
$C \in \operatorname{H}_b^\bullet (\pi _1(M))$
, we have
Lemma 5.1.
Let
![]() $M$
be a manifold and
$M$
be a manifold and
![]() $\omega$
a finite measure induced by a volume form on
$\omega$
a finite measure induced by a volume form on
![]() $M$
. Suppose that
$M$
. Suppose that
![]() $i\ :\ F \to \pi _1(M)$
is an embedding of a non-abelian free group
$i\ :\ F \to \pi _1(M)$
is an embedding of a non-abelian free group
![]() $F$
. There exists
$F$
. There exists
![]() $\Lambda \in \mathbb{R}$
such that for every
$\Lambda \in \mathbb{R}$
such that for every
![]() $\epsilon \gt 0$
there exists an
$\epsilon \gt 0$
there exists an
![]() $(F, \Lambda, \epsilon )$
-inverse of
$(F, \Lambda, \epsilon )$
-inverse of
![]() $\Gamma _b$
.
$\Gamma _b$
.
Proof. Let
![]() $\operatorname{dim}(M)=m$
. Denote by
$\operatorname{dim}(M)=m$
. Denote by
![]() $B^{m-1} \subset \mathbb{R}^{m-1}$
the
$B^{m-1} \subset \mathbb{R}^{m-1}$
the
![]() $m-1$
dimensional closed unit ball, and let
$m-1$
dimensional closed unit ball, and let
![]() $S^1 = \mathbb{R}/\mathbb{Z}$
. Let us fix
$S^1 = \mathbb{R}/\mathbb{Z}$
. Let us fix
![]() $\eta \in (0,1)$
and define an isotopy
$\eta \in (0,1)$
and define an isotopy
![]() $P^t_\eta \; \in \; \operatorname{Diff}(S^1 \times B^{m-1})$
by
$P^t_\eta \; \in \; \operatorname{Diff}(S^1 \times B^{m-1})$
by
where
![]() $t \in [0,1]$
and
$t \in [0,1]$
and
![]() $f\ :\ [0,1]\to \mathbb{R}$
is a smooth function such that
$f\ :\ [0,1]\to \mathbb{R}$
is a smooth function such that
![]() $f(y) = 1$
for
$f(y) = 1$
for
![]() $y \leq 1-\eta$
and
$y \leq 1-\eta$
and
![]() $f(1) = 0$
. We call
$f(1) = 0$
. We call
![]() $P^t_\eta$
the finger-pushing isotopy and
$P^t_\eta$
the finger-pushing isotopy and
![]() $P^1_\eta$
the finger-pushing map. Note that
$P^1_\eta$
the finger-pushing map. Note that
![]() $P^0_\eta = Id$
and that
$P^0_\eta = Id$
and that
![]() $P^1_\eta$
fixes point-wise the boundary of
$P^1_\eta$
fixes point-wise the boundary of
![]() $S^1 \times B^{m-1}$
and fixes all points
$S^1 \times B^{m-1}$
and fixes all points
![]() $(\psi, x)$
for which
$(\psi, x)$
for which
![]() $|\hspace{-1px}| x |\hspace{-1px}| \leq 1-\eta$
. Moreover,
$|\hspace{-1px}| x |\hspace{-1px}| \leq 1-\eta$
. Moreover,
![]() $P^t_\eta$
fixes the boundary of
$P^t_\eta$
fixes the boundary of
![]() $S^1 \times B^{m-1}$
for all
$S^1 \times B^{m-1}$
for all
![]() $t$
. Denote by
$t$
. Denote by
![]() $g_0$
be the product of the standard Euclidean Riemannian metrics on
$g_0$
be the product of the standard Euclidean Riemannian metrics on
![]() $B^{m-1}$
and
$B^{m-1}$
and
![]() $S^1$
. By the theorem of Fubini, the measure induced by
$S^1$
. By the theorem of Fubini, the measure induced by
![]() $g_0$
is preserved by the map
$g_0$
is preserved by the map
![]() $P^t_\eta$
for every
$P^t_\eta$
for every
![]() $t \in [0,1]$
. Let
$t \in [0,1]$
. Let
![]() $a_1,\ldots, a_k$
be generators of
$a_1,\ldots, a_k$
be generators of
![]() $F\,:\!=\,F_k$
, where
$F\,:\!=\,F_k$
, where
![]() $k\gt 1$
. We represent
$k\gt 1$
. We represent
![]() $i(a_i)$
by a loop
$i(a_i)$
by a loop
![]() $\alpha _i$
which is based at
$\alpha _i$
which is based at
![]() $* \in M$
.
$* \in M$
.
Let
![]() $B$
be a closed ball in
$B$
be a closed ball in
![]() $M$
containing
$M$
containing
![]() $*$
and set
$*$
and set
![]() $\Lambda = \omega (B)$
. Suppose
$\Lambda = \omega (B)$
. Suppose
![]() $A_i$
are closed small tubular neighborhoods of
$A_i$
are closed small tubular neighborhoods of
![]() $\alpha _i$
. Then
$\alpha _i$
. Then
![]() $N_i=B\cup A_i$
is a closed neighborhood of
$N_i=B\cup A_i$
is a closed neighborhood of
![]() $\alpha _i$
which is diffeomorphic to
$\alpha _i$
which is diffeomorphic to
![]() $S^1 \times B^{m-1}$
. Let
$S^1 \times B^{m-1}$
. Let
![]() $P^t_{\eta }(\alpha _i) \in \operatorname{Diff}_0(M)$
be the isotopy defined by pulling-back
$P^t_{\eta }(\alpha _i) \in \operatorname{Diff}_0(M)$
be the isotopy defined by pulling-back
![]() $P^t_{\eta }$
via a diffeomorphism
$P^t_{\eta }$
via a diffeomorphism
![]() $n_{\alpha _i}\ :\ N_i \to S^1 \times B^{m-1}$
(i.e., we have
$n_{\alpha _i}\ :\ N_i \to S^1 \times B^{m-1}$
(i.e., we have
![]() $P^t_{\eta }(\alpha _i) = n_{\alpha _i}^{-1} \circ P^t_{\eta } \circ n_{\alpha _i}$
on
$P^t_{\eta }(\alpha _i) = n_{\alpha _i}^{-1} \circ P^t_{\eta } \circ n_{\alpha _i}$
on
![]() $N_i$
) and extending it by the identity outside
$N_i$
) and extending it by the identity outside
![]() $N_i$
. Note that the Moser trick [Reference Moser17] allows us to choose
$N_i$
. Note that the Moser trick [Reference Moser17] allows us to choose
![]() $n_{\alpha _i}$
such that
$n_{\alpha _i}$
such that
![]() $P^t_{\eta }(\alpha _i)$
preserves
$P^t_{\eta }(\alpha _i)$
preserves
![]() $\omega$
. Let
$\omega$
. Let
![]() $S_i$
be the support of
$S_i$
be the support of
![]() $P^1_{\eta }(\alpha _i)$
. It is a small thickening of the boundary of
$P^1_{\eta }(\alpha _i)$
. It is a small thickening of the boundary of
![]() $N_i$
.
$N_i$
.
The homomorphism
![]() $\rho\ :\ F \to \operatorname{Homeo}_0\!(M,\omega )$
is given by:
$\rho\ :\ F \to \operatorname{Homeo}_0\!(M,\omega )$
is given by:
To simplify the notation, we identify
![]() $F$
with its image
$F$
with its image
![]() $i(F)$
. Now we consider the values of
$i(F)$
. Now we consider the values of
![]() $\gamma$
on elements of the form
$\gamma$
on elements of the form
![]() $(\rho (w),x)$
, where
$(\rho (w),x)$
, where
![]() $w\in F, x \in M$
.
$w\in F, x \in M$
.
From the description of
![]() $\gamma$
in Section 3.1, we have:
$\gamma$
in Section 3.1, we have:
 \begin{equation*} \gamma (\rho (w),x) = \begin {cases} e & x \in M-\bigcup _{i=1}^kN_i,\\ w & x \in B - \bigcup _{i=1}^k S_i,\\ ? & x \in (\bigcup _{i=1}^k A_i - B) \cup \bigcup _{i=1}^k S_i. \end {cases} \end{equation*}
\begin{equation*} \gamma (\rho (w),x) = \begin {cases} e & x \in M-\bigcup _{i=1}^kN_i,\\ w & x \in B - \bigcup _{i=1}^k S_i,\\ ? & x \in (\bigcup _{i=1}^k A_i - B) \cup \bigcup _{i=1}^k S_i. \end {cases} \end{equation*}
Let
![]() $C \in \operatorname{H}_b^n(M)$
, and let
$C \in \operatorname{H}_b^n(M)$
, and let
![]() $c$
be a bounded cochain representing
$c$
be a bounded cochain representing
![]() $C$
. Since any cochain and its anti-symmetrization define the same class, we may assume that
$C$
. Since any cochain and its anti-symmetrization define the same class, we may assume that
![]() $c(e,\ldots, e)\; =\; 0$
. Let
$c(e,\ldots, e)\; =\; 0$
. Let
and denote
Let
![]() $\overline{w} \in F^{n+1}$
. We have
$\overline{w} \in F^{n+1}$
. We have
Denote
![]() $E \,:\!=\,(\bigcup _{i=1}^k A_i - B) \cup \bigcup _{i=1}^k S_i$
. We obtain
$E \,:\!=\,(\bigcup _{i=1}^k A_i - B) \cup \bigcup _{i=1}^k S_i$
. We obtain
 \begin{align*} \rho ^*\Gamma _b (c)(\overline{w}) &= \int _{B - \bigcup _{i=1}^k S_i}c(\overline{w})d\omega (x) + \int _{E}c(\gamma (\rho (\overline{w}),x))d\omega (x)\\ &=\omega \left (B - \bigcup _{i=1}^k S_i\right )i^*(c)(\overline{w})+ \int _{E}c(\gamma (\rho (\overline{w}),x))d\omega (x). \end{align*}
\begin{align*} \rho ^*\Gamma _b (c)(\overline{w}) &= \int _{B - \bigcup _{i=1}^k S_i}c(\overline{w})d\omega (x) + \int _{E}c(\gamma (\rho (\overline{w}),x))d\omega (x)\\ &=\omega \left (B - \bigcup _{i=1}^k S_i\right )i^*(c)(\overline{w})+ \int _{E}c(\gamma (\rho (\overline{w}),x))d\omega (x). \end{align*}
Let
Note that
![]() $c_{res}$
represents a class in
$c_{res}$
represents a class in
![]() $\operatorname{H}_b^n(F)$
and we can write
$\operatorname{H}_b^n(F)$
and we can write
and
Moreover:
 \begin{align*} &|\hspace{-1px}| \rho ^*\Gamma _b (c)-\omega (B)i^*(c)|\hspace{-1px}|\leq \\ &\leq \omega (\bigcup _{i=1}^k S_i)|\hspace{-1px}| i^*(c)|\hspace{-1px}| +\omega (E)|\hspace{-1px}| c|\hspace{-1px}| \leq \\ & \leq \big [ \omega (\bigcup _{i=1}^k S_i) + \omega (E) \big ] |\hspace{-1px}| c |\hspace{-1px}|\ . \end{align*}
\begin{align*} &|\hspace{-1px}| \rho ^*\Gamma _b (c)-\omega (B)i^*(c)|\hspace{-1px}|\leq \\ &\leq \omega (\bigcup _{i=1}^k S_i)|\hspace{-1px}| i^*(c)|\hspace{-1px}| +\omega (E)|\hspace{-1px}| c|\hspace{-1px}| \leq \\ & \leq \big [ \omega (\bigcup _{i=1}^k S_i) + \omega (E) \big ] |\hspace{-1px}| c |\hspace{-1px}|\ . \end{align*}
Now
![]() $\omega (S_i)$
and
$\omega (S_i)$
and
![]() $\omega (E)$
can be taken to be arbitrarily small by taking small
$\omega (E)$
can be taken to be arbitrarily small by taking small
![]() $\eta$
and small neighborhoods
$\eta$
and small neighborhoods
![]() $A_i$
. The cochain
$A_i$
. The cochain
![]() $c$
was any cochain representing
$c$
was any cochain representing
![]() $C$
. Thus for any chosen
$C$
. Thus for any chosen
![]() $\epsilon$
, we can have
$\epsilon$
, we can have
where
![]() $\Lambda = \omega (B)$
.
$\Lambda = \omega (B)$
.
Theorem 5.2.
Let
![]() $M$
be an oriented manifold of dimension
$M$
be an oriented manifold of dimension
![]() $n$
such that it is either:
$n$
such that it is either:
-
• A hyperbolic surface with a non-abelian fundamental group or
-
• A complete hyperbolic
 $3$
-manifold whose fundamental group contains a geometrically infinite finitely generated free group (e.g.,
$3$
-manifold whose fundamental group contains a geometrically infinite finitely generated free group (e.g.,
 $M$
fibers over the circle with non-compact fiber).
$M$
fibers over the circle with non-compact fiber).
Let
![]() $\omega$
be a volume form on
$\omega$
be a volume form on
![]() $M$
such that the induced measure is finite. Then
$M$
such that the induced measure is finite. Then
![]() $\Gamma _b(Vol_M^{gp}) \in \operatorname{H}_b^n(\operatorname{Homeo}_0\!(M,\omega ))$
has positive norm.
$\Gamma _b(Vol_M^{gp}) \in \operatorname{H}_b^n(\operatorname{Homeo}_0\!(M,\omega ))$
has positive norm.
Proof. By Corollary 4.2 and Theorem4.3, in both cases, we have a free group
![]() $F$
and an embedding
$F$
and an embedding
![]() $i\ :\ F \to \pi _1(M)$
such that
$i\ :\ F \to \pi _1(M)$
such that
![]() $i^*(Vol_M^{gp})$
has positive norm. Let
$i^*(Vol_M^{gp})$
has positive norm. Let
![]() $\rho\ :\ F \to \operatorname{Homeo}_0(M,\omega _h)$
be an
$\rho\ :\ F \to \operatorname{Homeo}_0(M,\omega _h)$
be an
![]() $(F, \Lambda, \epsilon )$
-inverse of
$(F, \Lambda, \epsilon )$
-inverse of
![]() $\Gamma _b$
with
$\Gamma _b$
with
![]() $\epsilon$
satisfying
$\epsilon$
satisfying
We have
Thus
Since
![]() $\rho ^*$
is a contraction,
$\rho ^*$
is a contraction,
![]() $\Gamma _b (Vol_M^{gp})$
must have positive norm.
$\Gamma _b (Vol_M^{gp})$
must have positive norm.
Theorem 5.3.
Let
![]() $S$
be an oriented closed surface of genus
$S$
be an oriented closed surface of genus
![]() $\geq 2$
and
$\geq 2$
and
![]() $\omega$
a measure induced by an area form on
$\omega$
a measure induced by an area form on
![]() $S$
. Then the classes
$S$
. Then the classes
![]() $\Gamma _b(e_b^S) \in \operatorname{H}_b^2(\operatorname{Homeo}_0(S,\omega ))$
and
$\Gamma _b(e_b^S) \in \operatorname{H}_b^2(\operatorname{Homeo}_0(S,\omega ))$
and
![]() $\Gamma _b^{{\scriptscriptstyle \mathcal{M}_+}}(e_b^{{\scriptscriptstyle \mathcal{M}_+}}) \in \operatorname{H}_b^2(\operatorname{Homeo}(S,\omega ))$
have positive norms.
$\Gamma _b^{{\scriptscriptstyle \mathcal{M}_+}}(e_b^{{\scriptscriptstyle \mathcal{M}_+}}) \in \operatorname{H}_b^2(\operatorname{Homeo}(S,\omega ))$
have positive norms.
Proof. The proof for
![]() $e_b^S$
is the same as in Theorem5.2 using Lemma 4.5. Note that elements of
$e_b^S$
is the same as in Theorem5.2 using Lemma 4.5. Note that elements of
![]() $\operatorname{Homeo}(S,\omega )$
automatically preserve the orientation of
$\operatorname{Homeo}(S,\omega )$
automatically preserve the orientation of
![]() $S$
. Positivity of the norm of
$S$
. Positivity of the norm of
![]() $e_b^{{\scriptscriptstyle \mathcal{M}_+}}$
follows from the commutative diagram
$e_b^{{\scriptscriptstyle \mathcal{M}_+}}$
follows from the commutative diagram

where
![]() $Pu\ :\ \pi _1(S,*) \to \mathcal{M}_+(S,*)$
is the injection from the Birman exact sequence.
$Pu\ :\ \pi _1(S,*) \to \mathcal{M}_+(S,*)$
is the injection from the Birman exact sequence.
6. Dirac measure
The constructions of
![]() $\Gamma _{\hspace{-2px}b}$
and
$\Gamma _{\hspace{-2px}b}$
and
![]() $\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
are flexible and admit more variants. First of all, one does not need to restrict to measures coming from a volume form. What is needed is a measure with a cocycle for which the integral in the definition is well defined. Moreover, one can relax the definition of an isotopy. For example, it is not necessary to assume that isotopy preserves the measure at all times. Isotopy might be as well substituted by homotopy.
$\Gamma _{\hspace{-2px}b}^{\scriptscriptstyle \mathcal{M}}$
are flexible and admit more variants. First of all, one does not need to restrict to measures coming from a volume form. What is needed is a measure with a cocycle for which the integral in the definition is well defined. Moreover, one can relax the definition of an isotopy. For example, it is not necessary to assume that isotopy preserves the measure at all times. Isotopy might be as well substituted by homotopy.
In this short section, we discuss the (somewhat degenerate) case where the measure is the Dirac measure and isotopies do not preserve the measure. In this case,
![]() $\Gamma _{\hspace{-2px}b}$
is induced by a homomorphism. Let
$\Gamma _{\hspace{-2px}b}$
is induced by a homomorphism. Let
![]() $M$
be a manifold and
$M$
be a manifold and
![]() $* \in M$
a basepoint. We assume that the center of
$* \in M$
a basepoint. We assume that the center of
![]() $\pi _1(M,*)$
is trivial (what we really need to assume is the triviality of
$\pi _1(M,*)$
is trivial (what we really need to assume is the triviality of
![]() $ev_1$
, and even in the case where it is not, one could substitute
$ev_1$
, and even in the case where it is not, one could substitute
![]() $\pi _1(M,*)$
with the quotient
$\pi _1(M,*)$
with the quotient
![]() $\pi _1(M,*)/im(ev_1)$
). By
$\pi _1(M,*)/im(ev_1)$
). By
![]() $*$
we denote as well the Dirac measure centered on
$*$
we denote as well the Dirac measure centered on
![]() $*$
.
$*$
.
Let
![]() $G$
be the subgroup of
$G$
be the subgroup of
![]() $\operatorname{Homeo}_0(M)$
of all homeomorphisms
$\operatorname{Homeo}_0(M)$
of all homeomorphisms
![]() $f$
preserving
$f$
preserving
![]() $*$
. Thus an element of
$*$
. Thus an element of
![]() $G$
is isotopic to the identity by an isotopy that can move
$G$
is isotopic to the identity by an isotopy that can move
![]() $*$
. Suppose
$*$
. Suppose
![]() $S$
is a system of paths. As in Section 3.1, we get a cocycle:
$S$
is a system of paths. As in Section 3.1, we get a cocycle:
and a map
Note that on
![]() $\widetilde{M}$
, we can consider the counting measure on the orbit
$\widetilde{M}$
, we can consider the counting measure on the orbit
![]() $p^{-1}(*)$
. With such a measure
$p^{-1}(*)$
. With such a measure
![]() $\widetilde{M}$
defines a coupling and every
$\widetilde{M}$
defines a coupling and every
![]() $S$
is measurable. Moreover,
$S$
is measurable. Moreover,
![]() $\Gamma _b$
does not depend on
$\Gamma _b$
does not depend on
![]() $S$
[Reference Nitsche19, Lemma 3.3].
$S$
[Reference Nitsche19, Lemma 3.3].
Recall that we have a homomorphism
defined in the following way:
![]() $Tr(f)$
is the homotopy class of the loop
$Tr(f)$
is the homotopy class of the loop
![]() $f_t(*)$
, where
$f_t(*)$
, where
![]() $f_t$
is any isotopy between
$f_t$
is any isotopy between
![]() $Id_M$
and
$Id_M$
and
![]() $f$
.
$f$
.
It is straightforward to see that
![]() $\Gamma _b = Tr^*$
, the map induced on bounded cohomology by
$\Gamma _b = Tr^*$
, the map induced on bounded cohomology by
![]() $Tr$
. Note that if we started with the group
$Tr$
. Note that if we started with the group
![]() $\operatorname{Homeo}_0(M,*)$
(isotopies preserve
$\operatorname{Homeo}_0(M,*)$
(isotopies preserve
![]() $*$
at all times), instead of
$*$
at all times), instead of
![]() $G$
, then
$G$
, then
![]() $\Gamma _b\ :\ \operatorname{H}_b^\bullet (\pi _1(M,*)) \to \operatorname{H}_b^\bullet (\operatorname{Homeo}_0(M,*))$
would be trivial in positive degrees. Indeed, in this case
$\Gamma _b\ :\ \operatorname{H}_b^\bullet (\pi _1(M,*)) \to \operatorname{H}_b^\bullet (\operatorname{Homeo}_0(M,*))$
would be trivial in positive degrees. Indeed, in this case
![]() $\Gamma _b(c)$
is a constant cocycle, and constant cocycles in positive degrees represent trivial classes.
$\Gamma _b(c)$
is a constant cocycle, and constant cocycles in positive degrees represent trivial classes.
Suppose that a non-abelian free group
![]() $F$
embeds in
$F$
embeds in
![]() $\pi _1(M,*)$
. The representations
$\pi _1(M,*)$
. The representations
![]() $\rho$
constructed in Lemma 5.1 are homomorphisms. Since
$\rho$
constructed in Lemma 5.1 are homomorphisms. Since
![]() $\gamma (\rho (w),*) = w$
for every
$\gamma (\rho (w),*) = w$
for every
![]() $w \in F$
, the following diagram commutes:
$w \in F$
, the following diagram commutes:

Thus
![]() $\rho$
is a
$\rho$
is a
![]() $(F,1,0)$
-inverse of
$(F,1,0)$
-inverse of
![]() $\Gamma _{\hspace{-2px}b}$
. It follows that Theorems5.2 and 5.3 hold as well for the Dirac measure. Similarly, Theorem A and Theorem B from [Reference Brandenbursky and Marcinkowski5] hold with
$\Gamma _{\hspace{-2px}b}$
. It follows that Theorems5.2 and 5.3 hold as well for the Dirac measure. Similarly, Theorem A and Theorem B from [Reference Brandenbursky and Marcinkowski5] hold with
![]() $\mathcal{T}_M = G$
; that is,
$\mathcal{T}_M = G$
; that is,
![]() $Tr^*$
has the image of dimension continuum in degree
$Tr^*$
has the image of dimension continuum in degree
![]() $2$
and
$2$
and
![]() $3$
(if
$3$
(if
![]() $M$
satisfies the assumptions of Theorems A and B).
$M$
satisfies the assumptions of Theorems A and B).