Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T07:36:55.106Z Has data issue: false hasContentIssue false
  • English
  • Français

UNITARY FUNCTOR CALCULUS WITH REALITY

Part of: Homotopy theory Applied homological algebra and category theory

Published online by Cambridge University Press:  10 March 2021

NIALL TAGGART
NIALL TAGGART*
Affiliation:
Max Planck Institute for Mathematics, Vivatsgasse 7, 53111 Bonn, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct a calculus of functors in the spirit of orthogonal calculus, which is designed to study ‘functors with reality’ such as the Real classifying space functor, 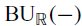. The calculus produces a Taylor tower, the n-th layer of which is classified by a spectrum with an action of 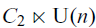. We further give model categorical considerations, producing a zigzag of Quillen equivalences between spectra with an action of 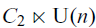and a model structure on the category of input functors which captures the homotopy theory of the n-th layer of the Taylor tower.

MSC classification

Primary: 55P65: Homotopy functors
Secondary: 55P42: Stable homotopy theory, spectra 55P91: Equivariant homotopy theory 55U35: Abstract and axiomatic homotopy theory
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 1 , January 2022 , pp. 197 - 230
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Footnotes

The author wishes to thank David Barnes for numerous helpful and insightful conversations and suggestions on this material.

References

Arone, G., The Weiss derivatives of BO(–) and BU(–), Topology 41(3) (2002), 451–481.CrossRefGoogle Scholar
Atiyah, M. F., K-theory and reality, Q. J. Math. 17(1) (1966), 367–386.CrossRefGoogle Scholar
Barnes, D. and Oman, P., Model categories for orthogonal calculus, Algebr. Geom. Topol. 13(2) (2013) 959–999.CrossRefGoogle Scholar
Bousfield, A. K., On the telescopic homotopy theory of spaces, Trans. Amer. Math. Soc. 353(6) (2001) 2391–2426.CrossRefGoogle Scholar
Dotto, E., Equivariant calculus of functors and -analyticity of real algebraic K-theory, J. Inst. Math. Jussieu 15(4) (2016), 829–883.CrossRefGoogle Scholar
Dotto, E., Equivariant diagrams of spaces, Algebr. Geom. Topol. 16(2) (2016), 1157–1202.CrossRefGoogle Scholar
Dotto, E., Higher equivariant excision, Adv. Math. 309 (2017), 1–96.CrossRefGoogle Scholar
Dotto, E. and Moi, K., Homotopy theory of G-diagrams and equivariant excision, Algebr. Geom. Topol. 16(1) (2016), 325–395.Google Scholar
Friedberg, S. H., Insel, A. J. and Spence, L. E., Linear algebra, 2nd edition (Prentice Hall, Inc., Englewood Cliffs, NJ, 1989).Google Scholar
Goodwillie, T. G., Calculus, I. The first derivative of pseudoisotopy theory, K-Theory 4(1) (1990), 1–27.CrossRefGoogle Scholar
Goodwillie, T. G., Calculus. II. Analytic functors, K-Theory 5(4) (1991/92), 295–332.CrossRefGoogle Scholar
Goodwillie, T. G., Calculus. III. Taylor series, Geom. Topol. 7 (2003), 645–711.Google Scholar
Greenlees, J. P. C. and Shipley, B., An algebraic model for free rational G-spectra for connected compact Lie groups G, Math. Z. 269(1–2) (2011), 373–400.CrossRefGoogle Scholar
Greenlees, J. P. C. and Shipley, B., An algebraic model for free rational G-spectra, Bull. Lond. Math. Soc. 46(1) (2014), 133–142.Google Scholar
Hill, M. A. and Meier, L., The C 2-spectrum Tmf1(3) and its invertible modules, Algebr. Geom. Topol. 17(4) (2017), 1953–2011.Google Scholar
Hirschhorn, P. S., Model categories and their localizations , Mathematical Surveys and Monographs, vol. 99 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Hovey, M., Model categories , Mathematical Surveys and Monographs, vol. 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Kedziorek, M., An algebraic model for rational G-spectra over an exceptional subgroup, Homology Homotopy Appl. 19(2) (2017), 289–312.CrossRefGoogle Scholar
Lind, J., Diagram spaces, diagram spectra, and spectra of units, ArXiv e-prints, August 2009.Google Scholar
Mandell, M. A. and May, J. P., Equivariant orthogonal spectra and S-modules, Mem. Amer. Math. Soc. 159(755) (2002), x+108.Google Scholar
Mandell, M. A., May, J. P., Schwede, S. and Shipley, B., Model categories of diagram spectra, Proc. London Math. Soc. (3) 82(2) (2001), 441–512.CrossRefGoogle Scholar
Pol, L. and Williamson, J., The left localization principle, completions, and cofree G-spectra, J. Pure Appl. Algebra (2020). https://doi.org/10.1016/j.jpaa.2020.106408.CrossRefGoogle Scholar
Schwede, S., Lectures on equivariant stable homotopy theory. http://www.math.uni-bonn.de/people/schwede/SymSpec-v3.pdf, 2019.CrossRefGoogle Scholar
Taggart, N., Unitary calculus: model categories and convergence, arXiv e-prints, arXiv:1911.08575, Nov 2019.Google Scholar
Taggart, N., Comparing the orthogonal and unitary functor calculi, arXiv e-prints, arXiv:2001.04485, Jan 2020.Google Scholar
Tynan, P. D., Equivariant Weiss calculus and loop spaces of Stiefel manifolds, Thesis (Ph.D.)–Harvard University (ProQuest LLC, Ann Arbor, MI, 2016).Google Scholar
Weiss, M., Orthogonal calculus, Trans. Amer. Math. Soc. 347(10) (1995), 3743–3796.CrossRefGoogle Scholar
Weiss, M., Erratum: “Orthogonal calculus”, Trans. Amer. Math. Soc. 350(2) (1998), 851–855.CrossRefGoogle Scholar