Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-18T15:00:51.419Z Has data issue: false hasContentIssue false
  • English
  • Français

ULTRAPOWERS OF BANACH ALGEBRAS AND MODULES

Published online by Cambridge University Press:  01 September 2008

MATTHEW DAWS
MATTHEW DAWS*
Affiliation:
School of Mathematics, University of Leeds, Leeds, LS2 9JT, UK e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Arens products are the standard way of extending the product from a Banach algebra 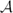to its bidual 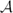″. Ultrapowers provide another method which is more symmetric, but one that in general will only give a bilinear map, which may not be associative. We show that if 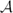is Arens regular, then there is at least one way to use an ultrapower to recover the Arens product, a result previously known for C*-algebras. Our main tool is a principle of local reflexivity result for modules and algebras.

Keywords

46B0746B0846H0546H2546L05
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 50 , Issue 3 , September 2008 , pp. 539 - 555
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Albiac, F. and Kalton, N. J., Topics in Banach space theory (Springer, New York, 2006).Google Scholar
2.Arens, R., The adjoint of a bilinear operation, Proc. Amer. Math. Soc. 2 (1951) 839–848.CrossRefGoogle Scholar
3.Behrends, E., On the principle of local reflexivity, Studia Math. 100 (1991) 109–128.CrossRefGoogle Scholar
4.Casazza, P. G., Approximation properties, in Handbook of the geometry of Banach spaces, Vol. I (Johnson, W. B. and Lindenstrauss, J., Editors) (North-Holland, Amsterdam, 2001), 271–316.CrossRefGoogle Scholar
5.Dales, H. G., Banach algebras and automatic continuity (Clarendon Press, Oxford, 2000).Google Scholar
6.Daws, M., Dual Banach algebras: Representations and injectivity, Studia Math. 178 (2007) 231–275.CrossRefGoogle Scholar
7.Daws, M., Banach algebras of operators, PhD Thesis (University of Leeds, 2005).Google Scholar
8.Defant, A. and Floret, K., Tensor norms and operator ideals (North-Holland Publishing Co., Amsterdam, 1993)Google Scholar
9.Diestel, J., Sequences and series and Banach spaces (Springer-Verlag, New York, 1984)CrossRefGoogle Scholar
10.Diestel, J. and Uhl, J. J. Jr., Vector measures (American Mathematical Society, Providence, RE, 1977)CrossRefGoogle Scholar
11.Ge, L. and Hadwin, D., Ultraproducts of C*-algebras, in Recent advances in operator theory and related topics (Birkhèuser, Basel, 2001), 305–326. Oper. Theory Adv. Appl., 127.CrossRefGoogle Scholar
12.Godefroy, G. and Iochum, B., Arens-regularity of Banach algebras and the geometry of Banach spaces, J. Funct. Anal. 80 (1988) 47–59.CrossRefGoogle Scholar
13.Heinrich, S., Ultraproducts in Banach space theory, J. reine angew. Math. 313 (1980) 72–104.Google Scholar
14.Iochum, B. and Loupias, G., Arens regularity and local reflexivity principle for Banach algebras, Math. Ann. 284 (1989) 23–40.CrossRefGoogle Scholar
15.Lau, A. T.-M., Uniformly continuous functionals on the Fourier algebra of any locally compact group, Trans. Amer. Math. Soc. 251 (1979) 39–59.CrossRefGoogle Scholar
16.Lau, A. T.-M. and Loy, R. J., Weak amenability of Banach algebras on locally compact groups, J. Funct. Anal. 145 (1997) 175–204.CrossRefGoogle Scholar
17.Palmer, T. W., Banach algebras and the general theory of *-algebras. Vol. 1. (Cambridge University Press, Cambridge, UK, 1994).CrossRefGoogle Scholar
18.Paulsen, V., Vern, , Completely bounded maps and operator algebras (Cambridge University Press, Cambridge, UK, 2002)Google Scholar
19.Quigg, J. C.Approximately periodic functionals on C*-algebras and von Neumann algebras, Canad. J. Math. 37 (1985) 769–784.CrossRefGoogle Scholar
20.Runde, V., Lectures on amenability (Springer-Verlag, Berlin, 2002).CrossRefGoogle Scholar
21.Runde, V., Amenability for dual Banach algebras Studia Math. 148 (2001) 47–66.CrossRefGoogle Scholar
22.Ryan, R., Introduction to tensor products of Banach spaces (Springer-Verlag, London, 2002).CrossRefGoogle Scholar
23.Takesaki, M., Theory of operator algebras I (Springer-Verlag, New York, 1979)CrossRefGoogle Scholar