Article contents
Two exponential Diophantine equations
Published online by Cambridge University Press: 18 May 2009
Extract
In [3], two open problems were whether either of the diophantine equations
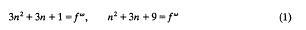
with n ∈ Z and f a prime number, is solvable if ω > 3 and 3 √ ω, but in this paper we allow f to be any (rational) integer and also 3 | ω. Equations of this form and more general ones can effectively be solved [5] with an advanced method based on analytical results, but the search limits are usually of enormous size. Here both equations (1) are norm equations in K (√–3): N(a + bp) = fw with p = (√–1 + –3)/2 which makes it possible to treat them arithmetically.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1997
References
REFERENCES
- 1
- Cited by


