No CrossRef data available.
Article contents
Totally real surfaces of the six-dimensional sphere
Published online by Cambridge University Press: 18 May 2009
Extract
An almost Hermitian manifold (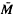 , J, g) with Riemannian connection
, J, g) with Riemannian connection 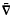 is called nearly Kaehlerian if (
is called nearly Kaehlerian if (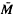 xJ)X = 0 for any
xJ)X = 0 for any 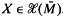 . The typical example is the sphere S6. The nearly Kaehlerian structure J for S6 is constructed in a natural way by making use of Cayley division algebra [3]. It is because of this nearly Kaehler, non-Kaehler, structure that S6 has attracted attention. Different classes of submanifolds of S6 have been considered by A. Gray [4], K. Sekigawa [5] and N. Ejiri [2]. In this paper we study 2-dimensional totally real submanifolds of S6. These are submanifolds with the property that for every x є M, J (Tx M) belongs to the normal bundle v. For this class we have obtained the following result.
. The typical example is the sphere S6. The nearly Kaehlerian structure J for S6 is constructed in a natural way by making use of Cayley division algebra [3]. It is because of this nearly Kaehler, non-Kaehler, structure that S6 has attracted attention. Different classes of submanifolds of S6 have been considered by A. Gray [4], K. Sekigawa [5] and N. Ejiri [2]. In this paper we study 2-dimensional totally real submanifolds of S6. These are submanifolds with the property that for every x є M, J (Tx M) belongs to the normal bundle v. For this class we have obtained the following result.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1991


