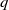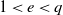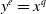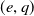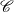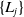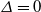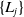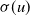Theory of heat equations for sigma functions

Abstract

Let $e$ and $q$ be fixed co-prime integers satisfying $1\lt e\lt q$. Let $\mathscr {C}$ be a certain family of deformations of the curve $y^e=x^q$. That family is called the $(e,q)$-curve and is one of the types of curves called plane telescopic curves. Let $\varDelta$ be the discriminant of $\mathscr {C}$. Following pioneering work by Buchstaber and Leykin (BL), we determine the canonical basis $\{ L_j \}$ of the space of derivations tangent to the variety $\varDelta =0$ and describe their specific properties. Such a set $\{ L_j \}$ gives rise to a system of linear partial differential equations (heat equations) satisfied by the function $\sigma (u)$ associated with $\mathscr {C}$, and eventually gives its explicit power series expansion. This is a natural generalisation of Weierstrass’ result on his sigma function. We attempt to give an accessible description of various aspects of the BL theory. Especially, the text contains detailed proofs for several useful formulae and known facts since we know of no works which include their proofs.

Introduction

Classically, the Weierstrass function $\sigma (u)$ is defined through the Weierstrass elliptic function $\wp (u)$ as follows:

\begin{align*} \sigma (u)=u\exp \!\bigg (\int _0^u\int _0^u\left(\tfrac 1{u^2} -\wp (u)\right)du\,du\bigg ). \end{align*}

The modern approach is to define the sigma function starting from a general elliptic curve. However, in this introduction, we treat only the curve defined by

(0.1) \begin{equation} y^2=x^3+\mu _4x+\mu _6 \ \ \ \textrm {(Weierstrass form)}. \end{equation}

(We refer the reader to [12] for the case of the most general elliptic curve.) For this curve, we define the function $\sigma (u)$ by

(0.2) \begin{equation} \sigma (u)=\left(\frac {2\pi }{\omega ^{\prime}}\right)^{1/2}\varDelta ^{{-}\frac 18}\, \exp \!\big ({-}\tfrac 12{\omega ^{\prime}}^{-1}\eta ^{\prime}u^2\big ) \cdot \vartheta \bigg [\, \begin{matrix} \frac 12 \\[3pt] \frac 12 \end{matrix}\, \bigg ]\!({\omega ^{\prime}}^{-1}u,\omega ^{\prime\prime}/\omega ^{\prime}), \end{equation}

where $\varDelta =-16(4{\mu _4}^3+27{\mu _6}^2)$ is the discriminant of the curve, and $\omega ^{\prime}$ , $\omega ^{\prime\prime}$ , $\eta ^{\prime}$ , and $\eta ^{\prime\prime}$ are the periods of the two differential forms

\begin{align*} \dfrac {dx}{2y}, \dfrac {xdx}{2y} \end{align*}

with respect to a pair of fixed standard closed paths $\alpha _1$ and $\beta _1$ which represents a symplectic basis of the first homology group, though $\eta ^{\prime\prime}$ does not appear explicitly. The last part of (0.2) is Jacobi’s theta series defined by

(0.3) \begin{equation} \vartheta \Big [\, \begin{matrix} b \\[-3pt] a \end{matrix}\, \Big ](z,\tau )=\sum _{n\in \mathbb {Z}} \exp 2\pi \boldsymbol {i}\big (\tfrac 12\tau (n+b)^2+(n+b)(z+a)\big ) \ \ \ \ (a,\ b\in \tfrac 12\mathbb {Z}). \end{equation}

From now on, we suppose the function $\sigma (u)$ is defined by (0.2). In using this definition, it is not clear that $\sigma (u)$ is independent of the choice of $\alpha _1$ and $\beta _1$ . Indeed, both of the later part (Jacobi’s theta series) of (0.2) and former part are not invariant when we choose another pair of $\alpha _1$ and $\beta _1$ . However, these changes offset each other and $\sigma (u)$ itself is invariant.

Using the Dedekind eta function $\eta (\tau )$ (not to be confused with the periods $\eta$ above and in Section 1.1), the discriminant $\varDelta$ of the curve above is given by $\varDelta =\big (\frac {2\pi }{\omega ^{\prime}}\big )^{12}\eta (\omega ^{\prime\prime}/\omega ^{\prime})^{24}$ , and the first terms in (0.2) can be explicitly written as

(0.4) \begin{equation} \left(\frac {2\pi }{\omega ^{\prime}}\right)^{1/2}\varDelta ^{-\frac 18} = -\frac {\ \omega ^{\prime}\,}{2\pi }\eta (\omega ^{\prime\prime}/\omega ^{\prime})^{-3}. \end{equation}

Although $\varDelta$ is invariant with respect to a change of $\alpha _1$ and $\beta _1$ , both sides of (0.4) and $\omega ^{\prime}$ are not invariant. The function $\sigma (u)$ has a power series expansion at the origin as follows:

(0.5) \begin{equation} \begin{aligned} \sigma (u)&= { u\sum _{\substack {n_4,n_6\geqq 0\\[3pt]}}b(n_4,n_6) \frac {(\mu _4u^4)^{n_4}(\mu _6u^6)^{n_6}}{(1+4n_4+6n_6)!} } \\[-3pt] &\ \ \ =u +2\mu _4\frac {u^5}{5!} +24\mu _6\frac {u^7}{7!} -36\mu _4^2\frac {u^9}{9!} -288\mu _4\mu _6\frac {u^{11}}{11!} +\cdots, \end{aligned} \end{equation}

where $b(n_4,n_6)\in \mathbb {Z}$ . (This expansion also shows the independence of $\sigma (u)$ with respect to the choice of $\alpha _1$ and $\beta _1$ ).

In this work, we are interested in the sigma function, which is a multivariate entire function, associated with a curve which we call $(n,s)$ -curves or plane telescopic curves (see Section 1.1 for definitions). One of the motivations of a theory of heat equations is to get a recurrence relation for the expansion coefficients of the sigma function, like that of the $b(n_4,n_6)$ s. But, there is another motivation as follows. For such a general non-singular curve, there is an intrinsic or axiomatic definition (see 4.1) of the sigma function. It would be useful if we have an expression, like (0.2), for the generalised sigma function. Indeed it is not so difficult to show that the natural generalisation of the right-hand side of (0.2), but dropping the factor corresponding to (0.4), satisfies some of the conditions in 4.1. Before [9], except for curves of genus one and two, the validity of the expression including the natural generalisation of the factor (0.4) was not yet proved completely. We shall discuss this motivation again at the end of this introduction.

It is well-known that the sigma function for a general non-singular algebraic curve is expressed by Riemann’s theta series with a characteristic coming from the Riemann constant of the curve multiplied by some exponential factor and some constant factor. This constant factor might be a natural generalisation of (0.4). But, there seems to be no proof of the determination of this constant factor except in genus one and two (we mention this again later). To fix the last constant is another motivation of the theory, which is described around Lemma 4.17 of [8].

We now review the classical theory of the heat equations for $\sigma (u)$ . Let $z$ and $\tau$ be complex numbers with the imaginary part of $\tau$ positive. We define $L=4\pi \boldsymbol {i}\frac {\partial }{\partial \tau }$ and $H=\frac {\partial ^2}{\partial {z}^2}$ . Then Jacobi’s theta function (0.3) satisfies the following equation, which is known as the heat equation,

(0.6) \begin{equation} (L-H)\,\vartheta \Big [\,\begin{matrix}b \\[-3pt] a \end{matrix}\,\Big ](z,\tau )=0. \end{equation}

Weierstrass’ result in [31], which is displayed as (0.13) below, is regarded as an interpretation of (0.6) in the form attached to his function $\sigma (u)$ . Strictly speaking, he did not derive it directly, but only by elementary and quite technical integrations from the well-known differential equation $\wp ^{\prime}(u)^2=4\wp (u)^3-g_2\wp (u)-g_3$ , where $g_2=-4\mu _4$ and $g_3=-4\mu _6$ , satisfied by the $\wp (u)=-\frac {d^2}{\,du^2\,}\log \sigma (u)$ . He eventually obtained the recurrence relation

(0.7) \begin{equation} \begin{aligned} b(n_4,& n_6)=\frac {2}{3}(4n_4+6n_6-1) (2n_4+3n_6-1)b(n_4-1,n_6)\\[3pt] &-\frac {8}{3}(n_6+1)b(n_4-2,n_6+1) +12(n_4+1)b(n_4+1,n_6-1) \end{aligned} \end{equation}

for the coefficients of the expansion (0.5) of $\sigma (u)$ (see also §6.3 and [25]).

Frobenius and Stickelberger approached (0.7) via a different method in their paper [14] which was published in the same year as [31]. Using the expansion

(0.8) \begin{equation} \wp (u)=\frac {1}{u^2}+\frac {g_2}{20}u^2+\frac {g_3}{28}u^4 +\frac {{g_2}^2}{1200}u^6+\cdots, \end{equation}

and the corresponding expansion of the Weierstrass function

\begin{align*} \zeta (u)=\frac 1u-\int _0^u\left(\wp (u)-\frac 1{u^2}\right)du \end{align*}

with

(0.9) \begin{equation} g_2=60\!\!\!\!\!\!\sum _{(n^{\prime},n^{\prime\prime})\neq (0,0)}\!\frac {1}{(n^{\prime}\omega ^{\prime}+n^{\prime\prime}\omega ^{\prime\prime})^4}, \ \ g_3=140\!\!\!\!\!\!\sum _{(n^{\prime},n^{\prime\prime})\neq (0,0)}\!\frac {1}{(n^{\prime}\omega ^{\prime}+n^{\prime\prime}\omega ^{\prime\prime})^6}, \end{equation}

they obtained the formulae

\begin{align*} \omega ^{\prime}\frac {\partial g_2}{\partial \omega ^{\prime}} +\omega ^{\prime\prime}\frac {\partial g_2}{\partial \omega ^{\prime\prime}}&=-4g_2,\ \ \ \ \omega ^{\prime}\frac {\partial g_3}{\partial \omega ^{\prime}} +\omega ^{\prime\prime}\frac {\partial g_3}{\partial \omega ^{\prime\prime}}=-6g_3,\\[3pt] \eta ^{\prime}\frac {\partial g_2}{\partial \omega ^{\prime}} +\eta ^{\prime\prime}\frac {\partial g_2}{\partial \omega ^{\prime\prime}}&=-6g_3, \ \ \ \ \eta ^{\prime}\frac {\partial g_3}{\partial \omega ^{\prime}} +\eta ^{\prime\prime}\frac {\partial g_3}{\partial \omega ^{\prime\prime}}=-\frac {1}{3} {g_2}^2, \end{align*}

where $\eta ^{\prime}=\zeta (u+\omega ^{\prime})-\zeta (u)$ , $\eta ^{\prime\prime}=\zeta (u+\omega ^{\prime\prime}) -\zeta (u)$ which are independent of $u$ , and (see (6.4))

(0.10) \begin{equation} \begin{aligned} \omega ^{\prime}\frac {\partial }{\partial \omega ^{\prime}} +\omega ^{\prime\prime}\frac {\partial }{\partial \omega ^{\prime\prime}} &=-4g_2\frac {\partial }{\partial g_2} -6g_3\frac {\partial }{\partial g_3}, \\[3pt] \eta ^{\prime}\frac {\partial }{\partial \omega ^{\prime}} +\eta ^{\prime\prime}\frac {\partial }{\partial \omega ^{\prime\prime}} &=-6g_3\frac {\partial }{\partial g_2} -\frac 13{g_2}^2\frac {\partial }{\partial g_3}. \end{aligned} \end{equation}

In our notation of the present paper, these operators (0.10) are denoted by $4L_0$ and $4L_2$ , respectively. Moreover, they found (p.318 in [14])

\begin{align*} \omega ^{\prime}\frac {\partial \eta ^{\prime}}{\partial \omega ^{\prime}}+\omega ^{\prime\prime}\frac {\partial \eta ^{\prime}} {\partial \omega ^{\prime\prime}}=\eta ^{\prime}, \ \ \ \omega ^{\prime}\frac {\partial \eta ^{\prime\prime}}{\partial \omega ^{\prime}}+\omega ^{\prime\prime}\frac {\partial \eta ^{\prime\prime}} {\partial \omega ^{\prime\prime}}=\eta ^{\prime\prime}. \end{align*}

and gave, on p.326 of [14], exactly the same system of heat equations in [31]. Observing the work of Weierstrass from the viewpoint of the paper [9], the left-hand sides of (0.10) correspond to $L=4\pi \boldsymbol {i}\frac {\partial }{\partial \tau }$ , namely the operations with respect to the period integrals $\tau$ or $\{\omega ^{\prime},\ \omega ^{\prime\prime},\ \eta ^{\prime},\ \eta ^{\prime\prime}\}$ of the curve, which adopt to the expression (0.2); while the right-hand sides of (0.10) are an interpretation of such operations in order to adopt to the expansion (0.5) of (0.2) given by [31]. Although we suspect there are fruitful correspondences between Weierstrass, Frobenius, and Stickelberger, the authors have no details of these.

It appears difficult to generalise the Weierstrass method to the higher genus cases. There is some hint in the work of Frobenius-Stickelberger to generalise the result to these cases. In order to do so, it seems necessary to have generalisation of relations (0.10). But we do not have naive generalisations of (0.8) and (0.9).

Recently, Buchstaber and Leykin were able to generalise the above results to the sigma functions of higher genus curves ( [9], see also [6–8]). In [9], Buchstaber and Leykin generalise (0.10) to higher genus curves by using the first de Rham cohomology $H_{\mathrm {dR}}^1$ of the curve over the base ring, that is the space of the differential forms of the second kind modulo the exact forms (see Section 5.1). The paper [9] is our main reference for our work. Understanding that paper requires some background on the basic theory of heat equations and singularity theory, so we will summarise their arguments and those of Frobenius and Stickelberger, with hopefully accessible explanations.

We shall explain their method by taking the curve (0.1) as an example. Firstly, we introduce a certain heat equation (the primary heat equation) satisfied by the function defined in (0.11) below, which is a generalisation of the individual terms of the series appearing in the definition (0.2) of $\sigma (u)$ . Let us take the subalgebra $\boldsymbol {L}$ generated by $L_0$ and $L_2$ over $\mathbb {Q}[\mu _4,\,\mu _6]$ in the Lie algebra generated by $\frac {\partial }{\partial \mu _4}$ and $\frac {\partial }{\partial \mu _6}$ . Thanks to a lemma due to Chevalley (Lemma 2.4) and the horizontal derivation formula given in [28] which is explained in Section 2.3, we see that the Lie algebra generated by $L_0$ and $L_2$ over $\mathbb {Q}[\mu _4,\mu _6]$ acts on $H_{\mathrm {dR}}^1$ . Take a symplectic basis $(\frac {dx}{2y},\ \frac {xdx}{2y})$ of $H_{\mathrm {dR}}^1$ with respect to a naturally defined inner product in $H_{\mathrm {dR}}^1$ (See (3.6)). Let

\begin{align*} \Gamma ^L = \bigg [\,\begin{array}{c@{\quad}c} -\beta &\ \alpha \\[3pt] -\gamma &\ \beta \end{array}\,\bigg ] \end{align*}

be the representation matrix of the action of an operator $L\in \boldsymbol {L}$ (see (5.1)), which is called a Gauss-Manin connection in [9]. Then we see that $\alpha$ , $\beta$ and $\gamma$ belong to $\mathbb {Q}[\mu _4,\mu _6]$ . Taking integrals along the set of closed paths $\alpha _1$ and $\beta _1$ which make a symplectic homology basis of the curve, we see that the action of $L$ gives a linear transformation of the period matrix (see (4.2))

\begin{align*} \varOmega =\bigg [\, \begin{array}{c@{\quad}c} \omega ^{\prime} &\ \omega ^{\prime\prime} \\[3pt] \eta ^{\prime} &\ \eta ^{\prime\prime} \end{array}\,\bigg ] \end{align*}

with respect to the basis $(\frac {dx}{2y},\ \frac {xdx}{2y})$ and paths $\alpha _1$ , $\beta _1$ . This transformation is also represented by $\Gamma ^L$ as $L(\varOmega )=\Gamma ^L\,\varOmega$ (see (5.2)). Moreover, we introduce another operator

\begin{align*} H^L=\frac 12\, \left[\frac {\partial }{\partial u}\ \ u \right] \bigg [ \begin{array}{r@{\quad}c} \alpha & \ \beta \\[3pt] \beta & \ \gamma \end{array} \bigg ] \bigg [ \begin{array}{c} \frac {\partial }{\partial u} \\[3pt] u \end{array} \bigg ] =\frac 12\left(\,{\alpha }\,\frac {\partial ^2}{\partial u^2} +2{\beta }\,u\frac {\partial }{\partial u} +{\gamma }\,u^2 +\beta \,\right). \end{align*}

Then the function

(0.11) \begin{equation} \begin{aligned} G(b,u,\varOmega ) &=\bigg (\frac {2\pi }\omega ^{\prime}\bigg )^{\frac 12}\, \exp \big ({-}\tfrac 12 \eta ^{\prime} \omega ^{\prime-1} u^2\big )\\[3pt] &\times \exp \left(\,2\pi i\big (\,\tfrac 12 \omega ^{\prime-1} \omega ^{\prime\prime}{b^{\prime\prime}}^2 + b^{\prime\prime}(\omega ^{\prime-1}u+b^{\prime})\,\big )\right), \end{aligned} \end{equation}

where $b=[\,b^{\prime}\ \ b^{\prime\prime}\,]$ is an arbitrary constant vector, satisfies the heat equation

(0.12) \begin{equation} (L-H^L)G(b,u,\varOmega )=0. \end{equation}

We call this (and its generalisation) the primary heat equation (Theorem 5.1). While checking the validity of (0.12) is rather complicated, no details are given by Buchstaber and Leykin, and the description of this equation in [9] is not entirely consistent. We denote the expression of the right-hand side (0.2) without $\varDelta ^{-\frac 18}$ by $\tilde {\sigma }(u)$ (see (5.23)). According to the above equation and the fact that $\tilde {\sigma }(u)$ is an infinite sum of the $G(b,u,\varOmega )$ s for various $b^{\prime}$ and $b^{\prime\prime}$ , we see that $(L-H^L)\,\tilde {\sigma }(u)=0$ .

At the next stage, we shall check the operators $L_0$ and $L_2$ give rise to a system of heat equations which are satisfied by the right-hand side of (0.2), including the factor $\varDelta ^{-\frac 18}$ . Indeed, these operators are tangent to the singular locus given by $\varDelta =0$ (see the former part of Subsection 5.5). The paper [9] uses knowledge of singularity theory and succeeds in generalising nicely the result of Weierstrass and Frobenius-Stickelberger. So we explain techniques from singularity theory to calculate $\varDelta$ (Lemma 1.21(1)) as well as the operators tangent to the variety defined by $\varDelta =0$ . This stage is carried out in Subsections 5.3 and 5.5 and the result is given in (5.39).

In summary, the system of heat equations for (0.1) obtained by Weierstrass is

(0.13) \begin{equation} \begin{aligned} (L_0-H^{L_0})\,\sigma (u) &=\left (4{\mu _4}\frac {\partial }{\partial \mu _4} +6{\mu _6}\frac {\partial }{\partial \mu _6} -u\frac {\partial }{\partial u}+1\,\right )\sigma (u)=0,\\[3pt] (L_2-H^{L_2})\,\sigma (u) &=\left (6{\mu _6}\frac {\partial }{\partial \mu _4} -\frac 43{\mu _4}^2\frac {\partial }{\partial \mu _6} -\frac 12\frac {\partial ^2}{\partial u^2} +\frac 16{\mu _4}u^2\,\right )\sigma (u)=0, \end{aligned} \end{equation}

which is reproved as (6.8). For the general curves, the corresponding results are given as Theorem 5.2 in the text.

It is very important to determine whether the system of heat equations we obtain characterises the sigma function. For the genus one case, it was seen by Weierstrass that the recurrence (0.7) determines all the coefficients if we give an arbitrary value for $b(0,0)$ . That is, the solution space of (0.7), as well as (0.13), is of dimension one.

For a general non-singular curve, we consider the multivariate function $\sigma (u)$ defined similarly to (0.2). We can check that the operators we obtain (of Theorem 5.2) kill $\sigma (u)$ . However, it is not clear whether the solution space is of dimension one over the base field. The authors could not find any reason which suggests that the solution space is one dimensional. Nevertheless, we shall show that, for any curve of genus less than or equal to three, the solution space is one dimensional by giving an explicit recurrence relation from the system of heat equations we obtain, which is described in Section 6.

Although our main results are in Subsections 6.5, 6.6, 6.7 and 6.8, we give a number of additional useful results, which may be known only by specialists, with detailed proofs in Section 5 and Subsection 6.2. Subsection 6.3 reproduces the classical result and it would be helpful to read the following Subsections. Subsection 6.4 is rewritten in a slightly different formulation (Hurwitz-type series expansion of $\sigma (u)$ ) from [8].

We shall explain here a notion called modality which was introduced by Arnol’d (see 1.3 for details). For any co-prime positive integers $(e,q)$ with $e\lt q$ , we consider a family of the curves found by certain deformations of the singularity at the origin of the curve $y^e=x^q$ (we do not use these words in the text of this paper). This family of curves is called the $(e,q)$ -curve, which is a type of plane telescopic curve. The number of parameters necessary for this deformation is less than or equal to $(e-1)(q-1)$ . The last number is twice the genus of a generic curve of the family. The difference between $(e-1)(q-1)$ and the number of parameters is called the modality of this family. For instance, the curve (0.1) is regarded as the whole of the semi-universal deformations of $y^2=x^3$ with two parameters $\mu _4$ and $\mu _6$ , which is equal to twice its genus (i.e. $2=1\times 2$ ). In this case, the modality is $0$ . It is known that the hyperelliptic curve given by such deformations in the case $e=2$ is of modality $0$ . There are only two types of non-hyperelliptic plane telescopic curves of modality $0$ , which are the trigonal quartic curve, the $(3,4)$ -curve (genus three), and the trigonal quintic curve, the $(3,5)$ -curve (genus four). Concerning these two curves, we treat only the former one, the $(3,4)$ -curve, in this paper. More general curves including the $(3,5)$ -curve are discussed in [28]. For a general hyperelliptic curve, we give its corresponding system of heat equations in Lemma 6.1. For any plane telescopic curve, we gave a simple formula for its modality in Proposition 1.10.

In the last paragraph of Section 2 in [9], there is some description of the positive modality case. On the one dimesionality problem of the solution space of the case $e=2$ and some positive modality cases, we refer the reader to the forthcoming paper [28].

We shall mention two additional consequences of this theory. Firstly, for hyperelliptic curves of genus less than or equal to three, we again prove partially the result of [27] on Hurwitz integrality of the expansion of the sigma function. For example it is obvious from (0.7) that $b(n_4,n_6)\in \mathbb {Z}[\frac 13]$ . Similar results are shown for the hyperelliptic curves of genus two and three. This idea was suggested to Y.Ô. by Buchstaber. Secondly, this theory of heat equations in turn helps the construction of the sigma function, as explained in Lemma 4.17 of [8] (see also Section 5.6).

However, it might be possible to approach this problem via the results of Bernatska [3, 4] to get the top factor for a hyperelliptic curve corresponding to that of (0.2).

The formula (0.2) is well-known for the curve (0.1), and its generalisation (see (4.16)) is proved for the genus two hyperelliptic curve by Grant [16] by using Thomae’s formula. For any curve in the family we have investigated, there is a rough explanation in Lemma 2.3 in p.98 of [7], but without using Thomae’s formula.

Here, we mention the discriminant for a plain telescopic curve $\mathscr {C}$ . There is nice algorithm using a certain determinant to compute the discriminant of $\mathscr {C}$ as explained in 1.21 and 5.36. However, there is still a gap in this theory; that is, we do not have a general proof of coincidence of the discriminant and the determinant. If we know the weight of the discriminant in general, our idea of the proof of 5.36 works well.

We explain here that BL theory indeed gives a method to prove such a formula as (0.2) on the sigma functions, at least, for our curves of genus less than or equal to three. Firstly, assuming the expression (0.2) to be the correct sigma function, we show that it satisfies the system of heat equations. On the other hand, as we mentioned above, the solution space of the system is one dimensional and the system of heat equations gives a recursion relation, by which we have the power series expansion of the solution as shown in Section 3. Especially, we see the solution space is of dimension one. Therefore, we have a proof that the assumed expression of the sigma indeed gives the sigma function up to a non-zero absolute constant. This result is the main theorem of the present paper (see Theorem 5.3).

Finally, one of the authors S.Y. wishes to point out to the reader that his contribution on this paper is limited to the proof of the case $e=2$ in Proposition 5.41.

Convention. We use the following convention. As usual, we denote by $\mathbb {Z}$ , $\mathbb {Q}$ , $\mathbb {R}$ , and $\mathbb {C}$ the ring of integers, the field of rationals, the field of real numbers, the field of complex numbers, respectively. We denote by $\boldsymbol {i}$ the imaginary unit. $\mathrm {Mat}(n,R)$ denotes the ring of square matrices of size $n$ with all the entries in a ring $R$ . $\mathrm {Sym}(n,R)$ denotes the set of symmetric matrix in $\mathrm {Mat}(n,R)$ . ${}^{t}{\!A}$ stands for the transpose of a matrix $A$ . ${}^{\mathrm {rev}}{\!A}$ denotes the matrix obtained by reversing orders both of the rows and the columns of a matrix $A$ .

1. Preliminaries

1.1. The curves

We shall use $e$ and $q$ instead of $n$ and $s$ , respectively, of the $(n,s)$ -curves, which was usual in many previous papers on generalised sigma functions. Especially, the name $(n,s)$ -curve (which comes from singularity theory) is used by Buchstaber and Leykin in their papers, but we wish to avoid confusion with the many $n$ used as subscripts in sections from Section 6 onward, and the use of $s$ for Schur polynomials in Subsection 4.1.

So, we let $e$ and $q$ be two fixed positive integers such that $e\lt q$ and $\gcd (e,q)=1$ . We define, for these integers, a polynomial of indeterminates $X$ and $Y$

(1.1) \begin{equation} f(X,Y)=Y^e-p_1(X)Y^{e-1}-\cdots -p_{e-1}(X)Y-p_e(X), \end{equation}

where $p_j(X)$ is a polynomial of $X$ of degree $\lceil \tfrac {jq}{e}\rceil$ or smaller and its coefficients, which are also indeterminates, are denoted by

(1.2) \begin{equation} \begin{aligned} p_j(X)&=\sum _{k:jq-ek\gt 0}\mu _{jq-ek}\,X^k \ \ \ (1\leq j\leq e-1),\\[3pt] p_e(X)&=X^q+\mu _{e(q-1)}X^{q-1}+\cdots +\mu _{eq}. \end{aligned} \end{equation}

Please note that the sign at the front of each $p_j(X)$ with $j\neq e$ in $f(X,Y)$ is different from previous papers written by some of the authors. The base ring over which we work is quite general. For simplicity, the reader may start by taking the field $\mathbb {C}$ of complex numbers and assume the $\mu _i$ s to be constants belonging to this field. Let $\mathscr {C}=\mathscr {C}_{{\mu }}^{e,q}$ be the projective curve defined by

(1.3) \begin{equation} f(x,y)=0 \end{equation}

having a unique point $\infty$ at infinity. This means $(x,y)$ is a generic point of $\mathscr {C}$ in the classical terminology.

As the general elliptic curve is defined by an equation of the form

\begin{align*} y^2-(\mu _1x+\mu _3)y=x^3+\mu _2x^2+\mu _4x+\mu _6, \end{align*}

the curves $\mathscr {C}$ discussed here are a natural generalisation of elliptic curves.

The reason why we omit the terms of $\mu _j$ with $j\lt 0$ from $f(X,Y)$ is seen in the proof of 1.17.

Basically our situation is that all the coefficients $\mu _j$ of $f(X,Y)$ should be indeterminates. We denote by $\mathbb {Q}[{\mu }]$ the ring generated over the rationals $\mathbb {Q}$ by all the $\mu _j$ s. Then we shall treat $\mathscr {C}$ as a scheme over the $\mathrm {Spec}\,\mathbb {Q}[\mu ]$ . Since we need to use analytic methods from time to time, we freely switch the standing position where $\mu _j$ s are assumed to be complex numbers or indeterminates.

This $\mathscr {C}$ should be called an $(e,q)$ -curve following Buchstaber, Enolskii, and Leykin [10], or a plane telescopic curve after the paper [21]. Assuming all the $\mu _j$ s are complex numbers, the genus of $\mathscr {C}$ is $(e-1)(q-1)/2$ provided that it is non-singular. We will use $g$ to denote this quantity throughout this paper whether the curve $\mathscr {C}$ is non-singular or singular as well as in the case of the $\mu _j$ s being indeterminates: $g=(e-1)(q-1)/2$ . In this paper, we denote by

\begin{align*} f_X(x,y)\ \ \text {or}\ \ f_1(x,y) \ \ \ \ \text {[\,resp.}\ \ f_{\,Y}(x,y)\ \ \text {or}\ \ f_2(x,y)] \end{align*}

the polynomials obtained by substitution $X=x$ , $Y=y$ for the partial derivative of the polynomial $f(X,Y)$ with respect to $X$ [ resp. $Y$ ]

Now we introduce a weight function as follows. For a point $(x,y)$ in the curve $\mathscr {C}$ given by (1.1), we define the weight $\mathrm {wt}()$ on $\mathbb {Q}[\mu ][x,y]$ and $\mathbb {Q}[\mu ][X,Y]$ by

(1.4) \begin{equation} \mathrm {wt}(\mu _j)=-j, \ \ \ \mathrm {wt}(x)=\mathrm {wt}(X)=-e, \ \ \ \mathrm {wt}(y)=\mathrm {wt}(Y)=-q. \end{equation}

Then all the equations for functions, power series, differential forms, and so on in this paper are of homogeneous weight. We see that $\mathrm {wt}\big (f(X,Y)\big )=-eq$ . We will extend the notion of weight (1.4) in Subsection 4.2.

1.2. Definition of the discriminant

We shall define the discriminant of the curve $\mathscr {C}$ .

Definition 1.5. Suppose all the $\mu _j$ s are indeterminates. The discriminant $\varDelta$ of the form $f(X,Y)$ or of the curve $\mathscr {C}$ defined by $f(x,y)=0$ is the polynomial (up to the signs $\pm$ ) of the least degree in the $\mu _j$ s with integer coefficients such that the greatest common divisor of the coefficients is $1$ , and every zero of $\varDelta$ corresponds exactly to the case that $\mathscr {C}$ has a singular point.

For a curve $\mathscr {C}_0$ given by some fixed constants $\mu _j\in \mathbb {C}$ , we always define its discriminant as the one obtained by substituting these constants to the discriminant $\varDelta$ defined in 1.5. For instance, if $(e,q)=(2,3)$ , then

\begin{align*} f(X,Y)=Y^2-(\mu _1X+\mu _3)Y-(X^3+\mu _2X^2+\mu _4X+\mu _6) \end{align*}

and its discriminant is given by

(1.6) \begin{equation} \begin{aligned} \varDelta &=-\mu _6{\mu _1}^6+\mu _3\mu _4{\mu _1}^5+(({-}{\mu _3}^2-12\mu _6)\mu _2+{\mu _4}^2){\mu _1}^4\\[3pt] &\ \ +(8\mu _3\mu _4\mu _2+{\mu _3}^3+36\mu _6\mu _3){\mu _1}^3+(({-}8{\mu _3}^2-48\mu _6){\mu _2}^2+8{\mu _4}^2\mu _2\\[3pt] &\ \ +({-}30{\mu _3}^2+72\mu _6)\mu _4){\mu _1}^2+(16\mu _3\mu _4{\mu _2}^2+(36{\mu _3}^3+144\mu _6\mu _3)\mu _2-96\mu _3{\mu _4}^2)\mu _1\\[3pt] &\ \ +({-}16{\mu _3}^2-64\mu _6){\mu _2}^3+16{\mu _4}^2{\mu _2}^2+(72{\mu _3}^2+288\mu _6)\mu _4\mu _2\\[3pt] &\ \ -64{\mu _4}^3-27{\mu _3}^4-216\mu _6{\mu _3}^2-432{\mu _6}^2. \end{aligned} \end{equation}

Specialising $\mu _1=\mu _3=\mu _2=0$ , we have the discriminant $\varDelta =-16(4{\mu _4}^3+27{\mu _6}^2)$ of the curve defined by the Weierstrass form $y^2=x^3+\mu _4x+\mu _6$ which appeared in (0.1).

For $(e,q)=(2,2g+1)$ , as in Section 1.3, we rewrite the equation as $y^2=x^{2g+1}+\cdots$ , where the right-hand side is a polynomial of $x$ only. Then the discriminant of this curve is a non-zero integer multiple of the discriminant of the right-hand side as a polynomial of $x$ only. For the $(3,4)$ -curve, we have Sylvester’s method as described in [15] pp.118-120, as explained to the authors by C. Ritzenthaler. However, Lemma 1.21 below gives a quite general method, which seems to cover the $(3,5)$ -curve and more. We do have explicit forms of the discriminants of the curves with $(e,q)=(2,3)$ , $(2,5)$ , $(2,7)$ , $(3,4)$ which we treat in this paper. Using the resultant of two forms, we mention here an alternative (but conjectural) construction for the interest of the reader, though it is essentially not used in this paper.

Definition 1.7. Let the coefficients $\mu _j$ of ( 1.1 ) be indeterminates, and define

\begin{align*} \begin{aligned} R_1&={\mathrm {rslt}}_X \left(\mathrm {rslt}_Y\big (f(X,Y), f_1(X,Y)\big ), \mathrm {rslt}_Y\big (f(X,Y), f_2(X,Y)\big ) \right), \\[3pt] R_2&=\mathrm {rslt}_Y \left(\mathrm {rslt}_X\big (f(X,Y), f_1(X,Y)\big ), \mathrm {rslt}_X\big (f(X,Y), f_2(X,Y)\big ) \right),\\[3pt] R&=\gcd (R_1,R_2)\ \ \ \ \textrm {in} \,\mathbb {Z}[{\mu }]. \end{aligned} \end{align*}

Here $\mathrm {rslt}_Z$ is the Sylvester resultant with respect to $Z$ .

Now we recall the conjecture from the paper [13].

Conjecture 1.8. Defining $R$ by 1.7, we have the following : (1) $R$ is always a perfect square in $\mathbb {Z}[\mu ]$ and $R=\varDelta ^2$ ; (2) The discriminant $\varDelta$ of the $(e,q)$ -curve is of weight $-2eqg=-eq(e-1)(q-1)$ .

Remark 1.9. It can be confirmed that (1) of 1.8 is correct for the cases $(e,q)=(2,3)$ , $(2,5)$ , $(2,7)$ , $(3,4)$ , and $(3,5)$ . Actually, computation by Maple for these cases shows that $R$ is a square of some $\varDelta ^{\prime}\in \mathbb {Z}[{\mu }]$ . It is easy to check by Maple that $\varDelta ^{\prime}$ is irreducible. Then, from the definition of $R$ , we see $\varDelta ^{\prime}$ must be $\varDelta$ up to the sign, and we checked (2) of 1.8 for these cases. We prove also that (2) of 1.8 is true if $\gcd (e-1,q-1)=1$ in 5.36.

1.3. The Weierstrass form of the curve and its modality

Starting from the equation $f(x,y)=0$ in (1.1) and removing the terms of $y^{e-1}$ and $x^{q-1}$ by replacing $y$ by $ y+\frac 1e\,p_1(x)$ , and $x$ by $ x+\frac 1q\mu _{(q-1)e}$ , respectively, we get a new equation $f(x,y)=0$ which is called the Weierstrass form of the original one. After making such transformations, we re-label the coefficients by $\mu _j$ .

For example, if $(e,q)=(2,2g+1)$ , the new equation is

\begin{align*} f(x,y)=y^2-(x^{2g+1}+\mu _{4g-2}x^{2g-1}+\mu _{4g-4}x^{2g-2}+\cdots +\mu _{4g+2})=0; \end{align*}

and if $(e,q)=(3,4)$ , the new one is

\begin{align*} f(x,y)=y^3-(\mu _2x^2+\mu _5x+\mu _8)y-(x^4+\mu _6x^2+\mu _9x+\mu _{12})=0. \end{align*}

In these cases, the number of remaining $\mu _j$ s is $2g$ . However, in general, we can have some cases such that this number is less than $2g$ . The difference

\begin{align*} 2g-\textrm {``the number of}\ \mu _j^{\prime\prime} \end{align*}

is called the modality (a term used in singularity theory) of the $(e,q)$ -curve. We give here a simple formula giving modalities and, especially, determine all the curves of modality $0$ .

Proposition 1.10. The modality of an $(e,q)$ -curve is given by $\frac 12(e-3)(q-3)+\lfloor \frac {q}{e}\rfloor -1$ . The only curves of modality $0$ are the $(2,2g+1)$ -, $(3,4)$ -, and $(3,5)$ -curves.

Proof. The number of $\mu _j$ s appearing in the Weierstrass form is

\begin{align*} \begin{aligned} \sum _{j=1}^{e-2}&\bigg (\bigg \lfloor \frac {(e-j)q}e\bigg \rfloor +1\bigg ) +(q-1) =\frac 12\sum _{j=1}^{e-1}\bigg (\bigg \lfloor \frac {(e-j)q}e\bigg \rfloor +\bigg \lfloor \frac {jq}e\bigg \rfloor \bigg )-\bigg \lfloor \frac {q}{e} \bigg \rfloor +(e-2)+(q-1)\\[3pt] &=\frac 12\sum _{j=1}^{e-1}(q-1)-\bigg \lfloor \frac {q}{e}\bigg \rfloor +e+q-3 =\frac 12(e-1)(q-1)+e+q-3-\bigg \lfloor \frac {q}{e}\bigg \rfloor . \end{aligned} \end{align*}

Subtracting the above result from $2g=(e-1)(q-1)$ gives the required expression. The latter part follows directly from this. This completes the proof.

On the case for a curve with positive modality, there is some description in [9] (the end of Section 2). Since it is not clear for us how positive modality causes difficulty, we do not discuss this theme here, though we give an example of positive modality in 1.16.

From now to the end of the paper, we always assume that the equation $f(x,y)=0$ of the curve $\mathscr {C}$ is given by a Weiserstrass form and the modality of $\mathscr{C}$ is 0.

1.4. Weight

We recall that (1.1), that is

\begin{align*} f(X,Y) =Y^e-X^q-\sum _{\substack {0\leq i\leq q-2\\[3pt]0\leq j\leq e-2\\[3pt]ie+jq\lt eq}}\mu _{eq-ie-jq}\,X^iY^j. \end{align*}

We define, for any pair $(i,j)$ with $0\leq i\leq q-2$ , $0\leq j\leq e-2$

(1.12) \begin{equation} \begin{aligned} M_{ei+qj}&=M_{ei+qj}(X,Y)=X^iY^j\ \textrm{and} \\[3pt] \mathrm {wt}(M)&=\{-\mathrm {wt}(X^iY^j)\,(\!=-\mathrm {wt}\big (M_{ei+qj}(X,Y)\big )\,|\,0\leq i\leq q-2, 0 \leq j\leq e-2\,\}\\[3pt] &=\{-(ei+qj)\,|\,0\leq i\leq q-2, 0\leq j\leq e-2\,\}. \end{aligned} \end{equation}

The sequence constituted by the elements in $-\mathrm {wt}(M)$ in increasing order is denoted by

\begin{align*} v_1(\!=0),\ v_2(\!=e), v_3, \ \cdots, \ v_{2g-2}, \ v_{2g-1}(\!=4g-2-e), \ v_{2g}(\!=4g-2). \end{align*}

Because of the assumption $\gcd (e,q)=1$ , for any $v\in \mathrm {wt}(M)$ there exists a unique pair $(i,j)$ such that $0\leq i\leq q-2$ , $0\leq j\leq e-2$ and $M_{v}=X^iY^j$ . We introduce the notation

(1.13) \begin{equation} \begin{aligned} M(X,Y)&={}^{t}{[\,M_{v_j}(X,Y) \ \ (j=1,2,\cdots, 2g)\,]}, \\[3pt] {}^{\mathrm {rev}}{M}(X,Y)&={}^{t}{[\,M_{v_j}(X,Y) \ \ (j=2g,2g-1,\cdots, 1)\,]}. \end{aligned} \end{equation}

We denote the Weierstrass gap sequence of the semigroup generated by $e$ and $q$ in the positive integers in the increasing order by

(1.14) \begin{equation} w_1(\!=1), \ w_2, \ \cdots, \ w_g(\!=2g-1), \end{equation}

which is also the Weierstrass gap sequence of $\mathscr {C}$ at $\infty$ . Namely, this is the unique (finite) increasing sequence of positive integers which cannot be written in the form $ae+bq$ with non-negative integers $a$ , $b$ . We denote the set of the terms in (1.14) by

\begin{align*} \mathrm {wgs}(e,\,q). \end{align*}

It is well-known that each term of the sequence is written in the form

\begin{align*} w_j=2g-1-v_{g-j+1} \ \ \ (1\leq j\leq g), \end{align*}

and that the assumption $\gcd (e,q)=1$ implies the Young tableaux associated with the sequence

\begin{align*} w_{2g}-(g-1), \ w_{2g-1}-(g-2), \ \cdots, \ w_2-1, \ w_1-0 \end{align*}

given by the Weierstrass gap sequences is symmetric with respect to the diagonal line from the top-left to the bottom-right. The terms in the sequence $\{v_j\}_{j=1}^{2g}$ are written also as

\begin{align*} v_j= \bigg \{\ \begin{aligned} &2g-1-w_{g-j+1} \ \ \ \textrm {if} \ 1\leq j\leq g,\\[3pt] &2g-1+w_{j-g} \ \ \ \ \ \textrm {if} \ g+1\leq j\leq 2g. \end{aligned} \end{align*}

We see that all the terms $\{M_{v_j}(X,Y)\}$ appear in $f(X,Y)$ provided the modality of the curve is $0$ . We shall give below sample values of the data above for the convenience of the reader to follow the calculation in Section 6.

Finally, we introduce the following notation on the coefficients $\mu _j$ ;

\begin{align*} \mu &=\{\,\mu _{eq-ie-jq}\,;\,0\leq i\leq q-2,\ 0\leq j\leq e-2,\ ie+jq\leq eq\,\}, \end{align*}

and

\begin{align*} \begin{aligned} \mathrm {wt}(\mu )&=\{-\mathrm {wt}(\mu _{eq-ie-jq})\,;\,0\leq i\leq q-2,\ 0\leq j\leq e-2, \ ie+jq\leq eq\,\}\\[3pt] &=\{-(eq-ie-jq)\,;\,0\leq i\leq q-2,\ 0\leq j\leq e-2, \ ie+jq\leq eq\,\}. \end{aligned} \end{align*}

Example 1.15. If $(e,q)=(2,2g+1)$ , then the $M_j$ s are given as follows:

If $(e,q)=(3,4)$ or $(3,5)$ , then the $M_j$ s are given as follows:

All these examples, and only these, are of modality $0$ as explained in (1.10).

Example 1.16. In contrast to the cases above, we have for $(e,q)=(3,7)$ :

However, the Weierstrass form of the $(3,7)$ -curve is given by

\begin{align*} \begin{aligned} Y^3&-(\mu _2X^4+\mu _5X^3+\mu _8X^2+\mu _{11}X +\mu _{14})Y\\[3pt] & -(X^7+\mu _6X^5+\mu _9X^4+\mu _{12}X^3+\mu _{15}X^3+\mu _{18}X+\mu _{21}) \end{aligned} \end{align*}

and this equation does not include a term in $M_{22}(X,Y)=X^5Y$ . This curve is of modality $1$ . We will not discuss this curve further in this paper.

1.5. The representation matrix for $f(X,Y)$ -multiplication

In this subsection, we shall define a certain matrix $T\in \mathrm {Mat}(2g,\mathbb {Q}[\mu ])$ whose determinant might be essentially the discriminant of $\varDelta$ .

Lemma 1.17. As a $\mathbb {Q}[\mu ]$ -module, $\mathbb {Q}[\mu ][X,Y]/(f_1(X,Y),f_2(X,Y))$ is of rank $2g$ and spanned by $M(X,Y)$ which is defined in ( 1.13 ).

Proof. (1) Let $G(X,Y)$ be any element in $\mathbb {Q}[\mu, X,Y]$ . Paying attention to the weight with respect to $X$ and $Y$ , we are reducing the terms in $G(X,Y)$ to lower degree by using $f_1(X,Y)=\cdots -qX^{q-1}+\cdots$ and $f_2(X,Y)=eY^{e-1}+\cdots$ . Whenever we reduce degrees of highest weight term(s) of $G(X,Y)$ by using one of these relations, $G(X,Y)$ is replaced by a lower degree polynomial. So we will finally arrived at a polynomial that is a linear combination of only terms in $M(X,Y)$ .

Definition 1.18. The transpose of the representation matrix of the $({-}eq)f(X,Y)$ -plication map

(1.19) \begin{equation} \cdot ({-}eq)\,f(X,Y)\,:\,\mathbb {Q}[\boldsymbol {\mu }][X,Y]/(f_1,f_2)\longmapsto \mathbb {Q}[\boldsymbol {\mu }][X,Y]/(f_1,f_2) \end{equation}

with respect to the basis $M(X,Y)$ is denoted by $T\in \mathrm {Mat}(2g,\,\mathbb {Q}[\mu ])$ , that is

(1.20) \begin{equation} -eq\,f(X,Y)M(X,Y)\equiv M(X,Y)\,{}^{t}{T}\,\bmod {(f_1,\,f_2)}. \end{equation}

We define the subscript of the entries in $T$ as follows. The row-index $a$ runs through $\mathrm {wt}(M)$ in increasing order, and $b$ runs through $\mathrm {wt}(\widetilde {\mu })$ in decreasing order, and we write

\begin{align*} T=[\,T_{a,b}\,]\in \mathrm {Mat}(2g,\,\mathbb {Q}[\mu ]) \end{align*}

Then we have $\mathrm {wt}(T_{a,b}){=}-(a+b)$ . This is written in the usual manner as $T\,{=}\,[T_{v_i,\,eq-v_{2g+1-j}}]$ .

One of the reasons why we have an extra factor $-eq$ in (1.19) appears in 5.33 later.

Lemma 1.21. We have the following:

1. 1. The determinant $\det (T)$ of the matrix $T$ as defined in 1.18 is a non-zero rational constant multiple of a power of $\varDelta$ .

2. 2. The linear map (1.19) is of rank $2g$ .

Proof. (1) We assume all the coefficients $\mu _j$ are constants in $\mathbb {C}$ . We have $\mathrm {det}(T)=0$ if and only if the rank (called the Tjurina number at $\mu$ ) of the co-kernel $\mathbb {Q}[\mu ][X,Y]/(f,f_1,f_2)=\mathbb {Q}[x,y]/(f_1,f_2)$ (which is the dimension of $\mathbb {C}[X,Y]/(f,f_1,f_2)$ over $\mathbb {C}$ ) of the map is positive. This is exactly the case that the ideal $(f,f_1,f_2)$ does not contain $1\in \mathbb {Q}[\mu ][X,Y]$ . By Hilbert’s Nullstellensatz (Theorem 5.4(i) in [20], for instance), we see this is equivalent to existence of a $(x,y)\in \mathbb {C}^2$ such that

(1.22) \begin{equation} f(x,y)=f_1(x,y)=f_2(x,y)=0. \end{equation}

Conversely $\varDelta =0$ means (1.22), and it implies the co-kernel is non-trivial. Therefore the zeroes of $\varDelta$ and those of $\det (T)$ coincide. So $\det (T)$ must be a non-zero rational constant multiple of a power of $\varDelta$ . (2) Since $\det (T)\neq 0$ by virtue of (1), this is obvious.

Now we present the following:

Conjecture 1.23. The determinant $\det (T)$ is irreducible in $\mathbb {Q}[\mu ]$ .

For each $(e,q)$ , if this conjecture is true then we have immediately from 1.21 that

\begin{align*} \det (T)=c\cdot \varDelta \ \ \ \text {for some $c\in \mathbb {Q}^{\times }$}. \end{align*}

We give the explicit value of $c$ above for the cases in Sections 6.3, 6.4, 6.5 and 6.7.

2. The horizontal derivation formula

Much of this section was lacking in the previous versions of this paper. However, the authors are pleased that the horizontal derivation formula (see 2.1 below) and its closely related results been used in the work of [28], and these results make our arguments in the rest of the present paper much clearer.

2.1. Preliminary on derivations

In this subsection, we prepare a general notation for the succeeding subsections. Let $A$ be a commutative ring. A map $D\,:\,A\longrightarrow A$ , $a\mapsto Da$ satisfying the following properties is called a derivation on $A$ ; for any $a$ , $b\in A$ ,

\begin{align*} D(a+b)=Da+Db, \ \ \ D(ab)=(Da)b+a(Db). \end{align*}

We denote by $\mathrm {Der}(A)$ the set of all derivations on $A$ , which is an $A$ -module. Since $\mathrm {Der}(A)$ is equipped with the natural Lie bracket

\begin{align*} [D_1,\ D_2]=D_1D_2-D_2D_1 \ \ \ (D_1, \ D_2\in \mathrm {Der}(A)), \end{align*}

$\mathrm {Der}(A)$ is a Lie algebra over $A$ . Let $M$ and $N$ be two $A$ -modules and $D\in \mathrm {Der}(A)$ be a fixed derivation on $A$ . A map $\widetilde {D}\,:\,M\longrightarrow N$ , $m\mapsto \widetilde {D}m$ satisfying

\begin{align*} \widetilde {D}(m_1+m_2)=\widetilde {D}m_1+\widetilde {D}m_2, \ \ \ \widetilde {D}(am)=(Da)m+a\widetilde {D}m \end{align*}

is called a derivation from $M$ to $N$ associated with $D$ . We denote by $\mathrm {Der}_A(M,N;D)$ the set of the derivations from $M$ to $N$ associated with $D$ . If $M=N$ , then we denote this simply by $\mathrm {Der}_A(M;D)=\mathrm {Der}_A(M,M;D)$ . Let $D_1$ , $D_2\in \mathrm {Der}(A)$ , and $\widetilde {D_1}\in \mathrm {Der}_A(M,N;D_1)$ , $\widetilde {D_2}\in \mathrm {Der}_A(M,N;D_2)$ . Then we see that

\begin{align*} a\widetilde {D_1}\in \mathrm {Der}_A(M,N;aD_1) \ \ (a\in A), \ \ \ \widetilde {D_1}+\widetilde {D_2}\in \mathrm {Der}_A(M,N;\,D_1+D_2). \end{align*}

Now let $B$ be an $A$ -algebra and take a derivative $D\in \mathrm {Der}(A)$ . Let $M$ and $N$ be two $B$ -modules, hence also $A$ -modules. Regarding $B$ as an $A$ -module, we take a derivation $\widetilde {D}\in \mathrm {Der}_A(B;D)$ associated with $D\in \mathrm {Der}(A)$ . Since we can regard naturally $\widetilde {D}\in \mathrm {Der}(B)$ , we have the inclusion

\begin{align*} \mathrm {Der}_B(M,N;\widetilde {D})\subset \mathrm {Der}_A(M,N;D). \end{align*}

For $\widetilde {D_1}\in \mathrm {Der}_A(M;D_1)$ , $\widetilde {D_2}\in \mathrm {Der}_A(M;D_2)$ , and for any $a\in A$ , $m\in M$ , we have

\begin{align*} [\widetilde {D_1},\ \widetilde {D_2}]\ (\!=\widetilde {D_1}\widetilde {D_2} -\widetilde {D_2}\widetilde {D_1}) \in \mathrm {Der}_A(M;[D_1,D_2]), \end{align*}

since $\widetilde {D_1}\widetilde {D_2}(am) =(D_1D_2a)m+(D_2a)(\widetilde {D_1}m)+(D_1a)(\widetilde {D_2}m) +a\widetilde {D_1}\widetilde {D}_2m$ . This implies that if $\widetilde {D_1}$ and $\widetilde {D_2}\in \mathrm {Der}_A(M;D)$ for a derivation $D\in \mathrm {Der}(A)$ , then

\begin{align*} [\widetilde {D_1},\ \widetilde {D_2}]\in \mathrm {Der}_A(M;0), \end{align*}

where $0$ stands for the $0$ -map from $A$ to $A$ itself, which is a derivation on $A$ . Namely, $[\widetilde {D_1},\ \widetilde {D_2}]$ is a $A$ -homomorphism. In the set of all maps from $M$ to $M$ , we take union of these sets over $\mathrm {Der}(A)$ and denote it as

\begin{align*} \mathrm {Der}_A(M)=\bigcup _{D\in \mathrm {Der}(A)}\mathrm {Der}_A(M;D). \end{align*}

This is also a Lie algebra over $A$ . Instead of writing $D\in \mathrm {Der}_A(M)$ , we can also say that the derivation $D$ acts on $M$ , for instance.

2.2. Chevalley’s lemma

We quote the following without proof from [11], p.112, Lemma 2.

Lemma 2.1. Let $K$ be a field and $R$ be a function field of one variable with $K$ the field of constants. Take a transcendental element $\xi$ in $R$ over $K$ and fix it. For $D\in \mathrm {Der}(K)$ , there exists a unique derivation $D_{\xi }\in \mathrm {Der}_K(R;D)$ satisfying

\begin{align*} D_{\xi }(\xi )=0. \end{align*}

Corollary 2.2. Suppose a derivation $D\in \mathrm {Der}(\mathbb {Q}[\mu ])$ and an element $\xi$ in $\mathbb {Q}[\mu, x,y]$ transcendental over $\mathbb {Q}(\mu )$ are given. There is a unique extension $D_{\xi }\in \mathrm {Der}_{\mathbb {Q}[\mu ]}(\mathbb {Q}(\mu, x,y),D)$ of $D$ satisfying

\begin{align*} D_{\xi }(\xi )=0. \end{align*}

Proof. We regard $\xi$ to be an element in $\mathbb {Q}(\mu, x,y)$ . Since $D$ extends to an element in $\mathrm {Der}(\mathbb {Q}(\mu ))$ as usual, the statement follows from 2.1.

Under the situation of 2.1, we extends $D_{\xi }$ to a derivation $\widetilde {D_{\xi }}$ on the space of differentials $R\,d\xi$ via

(2.3) \begin{equation} \widetilde {D_{\xi }}(\omega )=D_{\xi }\left(\frac {\omega }{d\xi }\right)d\xi \ \ \ \textrm {for} any \omega \in {R}\,d\xi . \end{equation}

Namely, we have $\widetilde {D_{\xi }}\in \mathrm {Der}_R(R\,d\xi ;\,D_{\xi })\subset \mathrm {Der}_K(R\,d\xi ;\,D)$ . However, in the following lemma, $\widetilde {D_{\xi }}$ is denoted by $D_{\xi }$ for simplicity.

Lemma 2.4. (Chevalley [11], p.125, Lemma 3) Here we use the notation above. Let $\xi$ and $\zeta$ be two transcendental elements in $R$ over $K$ . Then we have the following relation between $D_{\xi }$ and $D_{\zeta }$ . For any $w\in {R}$ , we have

\begin{align*} D_{\xi }(wd\xi ) - D_{\zeta }(wd\xi ) = d({-}wD_{\zeta }\xi ). \end{align*}

Proof. (From Manin [19]) The operator $D_{\xi }-D_{\zeta }+(D_{\zeta }\xi )\frac {d}{d\xi }$ is a derivative on $R$ which vanishes on $K$ and also kills $\xi$ . By the uniqueness of extension of a derivation on $K$ to $R$ , this vanishes on $R$ . So that

\begin{align*} (D_{\xi }-D_{\zeta })w+(D_{\zeta }\xi )\frac {dw}{d\xi }=0. \end{align*}

Moreover $(D_{\xi }-D_{\zeta })(wd\xi )=(D_{\xi }-D_{\zeta })w\cdot {d\xi } +w\cdot (D_{\xi }-D_{\zeta })d\xi$ . Since $\zeta$ is transcendental, we see $\frac {d}{d\zeta }D_{\zeta }=D_{\zeta }\frac {d}{d\zeta }$ by 2.16 below or [11], p.125, Lemma 1, and have

\begin{align*} D_{\xi }d\xi =D_{\xi }\left(\frac {d\xi }{d\xi }\right)d\xi =0,\ \ \ D_{\zeta }d\xi =D_{\zeta }\left(\frac {d\xi }{d\zeta }\right)d\zeta = \frac {d}{d\zeta }(D_{\zeta }\xi )d\zeta =d\big (D_{\zeta }(\xi )\big ). \end{align*}

Therefore

\begin{align*} (D_{\xi }-D_{\zeta })(wd\xi )=-(D_{\zeta }\,\xi )\frac {dw}{d\xi }d\xi -w{\cdot }d(D_{\zeta }\,\xi )=-d(wD_{\zeta }\,\xi ) \end{align*}

as desired.

For an explicit sample calculation, see Section 6.3 on the derivation $\frac {\partial }{\partial \mu _j}$ .

2.3. The horizontal derivation formula

We present a useful formula 2.1 called the horizontal derivation formula, which is important for our definition of the first de Rham cohomology equipped with a structure of a differential module and eventually giving a sophisticated algorithm to compute the Gauss-Manin connection $\varGamma _j$ (a sort of Christoffel symbol). The formula was obtained by Kouki Sato while working on [28], and coauthors of that paper have permitted us to quote from it. This formula would be useful for various applications.

In addition to the matrix $T=[T_{ij}]$ in 1.18, we introduce $A_{i+e}$ and $B_{i+e}\in \mathbb {Q}[\mu, X,Y]$ for each $i\in \mathrm {wt}(M)$ defined by

(2.5) \begin{equation} -eq\cdot {}M_i\cdot {f}(X,Y)=\sum _{j\,\in \mathrm {wt}(M)}T_{ij}M_j+A_{i+e}\, f_X+B_{i+q}\,f_{\,Y}, \end{equation}

where $f(X,Y)$ is the defining polynomial of $\mathscr {C}$ and $M_i=M_i(X,Y)$ is the one defined in 1.12. In this notation, we have

\begin{align*} \mathrm {wt}(A_{i+e})=-(i+e), \ \ \ \mathrm {wt}(B_{i+q})=-(i+q). \end{align*}

We denote by

\begin{align*} \frac {\,\partial \,}{\partial \mu _j\,}\in \mathrm {Der}_{\mathbb {Q}[\mu ]}\left(\mathbb {Q}(\mu, x,y);\frac {\,\partial \,}{\partial \mu _j\,}\right) \end{align*}

the derivation uniquely determined by 2.2 as an extension of the derivation $\frac {\,\partial \,}{\partial \mu _j\,}\in \mathrm {Der}(\mathbb {Q}[\mu ])$ having the property

(2.6) \begin{equation} \frac {\,\partial \,}{\partial \mu _j\,}x=0. \end{equation}

Namely, we use the same notation for the extension. It is natural to define the weight to be

(2.7) \begin{equation} \mathrm {wt}\left (\frac {\,\partial \,}{\partial \mu _j\,}\right )=j. \end{equation}

Moreover, there is a unique extension $\widetilde {\ell _i}$ of the derivation

(2.8) \begin{equation} \ell _i=\sum _jT_{ij}\,\frac {\,\partial \,}{\partial \mu _j\,}\in \mathrm {Der}(\mathbb {Q}[\mu ]) \end{equation}

satisfying

\begin{align*} \widetilde {\ell _i}x=0, \end{align*}

by 2.2 again, for which we use the same notation

(2.9) \begin{equation} \widetilde {\ell _i}=\sum _jT_{ij}\,\frac {\,\partial \,}{\partial \mu _j\,} \in \mathrm {Der}_{\mathbb {Q}[\mu ]}(\mathbb {Q}(\mu, x,y);\ell _i). \end{equation}

Therefore, for a 1-form $\omega \in \mathbb {Q}(\mu, x,y)\,dx$ , defining $\overline {\ell _i}$ by

\begin{align*} \overline {\ell _j}(\omega )=\widetilde {\ell _j}\left(\frac {\omega }{\,dx\,}\right)dx \end{align*}

as (2.3) (be careful as this depends on the condition (2.6)), and we have an extension

(2.10) \begin{equation} \overline {\ell _i}\in \mathrm {Der}_{\mathbb {Q}[\mu ]}(\mathbb {Q}(\mu, x,y)dx;\ell _i). \end{equation}

However, we omit $\ \widetilde {\ }\; $ and ${\overline {\phantom{\ell _i} }}$ for simplicity, and use the notation

\begin{align*} \ell _i=\sum _jT_{ij}\,\frac {\,\partial \,}{\partial \mu _j\,} \end{align*}

for these extensions. This convention will be practical.

In this paper, for a polynomial $G=G(\mu, X,Y)\in \mathbb {Q}[\mu, X,Y]$ , we denote by $(G)_x=G_x$ , $(G)_y=G_y$ , and $(G)_{\mu _j}=G_{\mu _j}$ the polynomials given by the substitution $(X,Y)=(x,y)$ to the partial derivations $\frac {\partial }{\,\partial X}\,{G}(\mu, X,Y)$ , $\frac {\partial }{\,\partial X}\,{G}(\mu, X,Y)$ , and $\frac {\partial }{\,\partial \mu _j}\,{G}(\mu, X,Y)$ . This rule is applied also for $f(X,Y)$ . Moreover, the higher-order case is similarly defined. For example, $f_{yy}$ means the quantity given by the substitution $(X,Y)=(x,y)$ to $\frac {\partial ^2}{\,\partial Y^2\,}f(X,Y)$ .

Under this convention, we present the following formula, which is mainly used for 3.2.

Theorem 2.11. (the horizontal derivation formula) Let $N=N(X,Y)$ be a monomial of $X$ and $Y$ (with non-negative powers), and $P\in \mathbb {Q}[\mu ]$ be an arbitrary polynomial. Then we have the following formula :

(2.11) \begin{align} \ell _j \left(\frac {\,P\cdot N\,}{f_y}\,dx \right) & = P\,\frac {(N)_y\,B_{j+q}-N\big (M_j+(B_{j+q})_y\big )-(N\,A_{j+e})_x}{f_y}\,dx \nonumber \\[3pt] & \qquad \qquad + \ell _j(P)N\,\frac {\,dx\,}{f_y}+d\bigg (P\,\frac {\,NA_{j+e}\,}{f_y}\bigg ). \end{align}

Especially, if $e=2$ then we have

\begin{align*} \ell _j\bigg (\frac {\,M_k\,dx\,}{f_y}\bigg ) =\frac {\,-(M_k\,A_{j+2})_x-M_{j+k}\,}{2y}\,dx+d\bigg (\frac {\,M_k\,A_{j+2}\,}{f_y}\bigg ). \end{align*}

Remark 2.13. The formula ( 2.11 ) shows

(2.14) \begin{equation} \ell _j\in \mathrm {Der}_{\mathbb {Q}[\mu ]}\left(\mathbb {Q}[\mu, x,y]\frac {\,dx\,}{f_y},\ \mathbb {Q}[\mu, \,x,\,y]\frac {\,dx\,}{f_y} +d\,\left(\mathbb {Q}[\,\mu, \,x,\,y]\frac {1}{\,f_y\,}\right) \,;\ \ell _j\right). \end{equation}

Since $\det (T)$ equals $\varDelta$ up to a non-zero rational multiplicative constant (see 1.21(3) and 5.36 below) at least in our cases $(e,q)=(2,3)$ , $(2,5)$ , $(2,7)$ , and $(3,4)$ , we also have

\begin{align*} \frac {\,\partial \,}{\partial \mu _j\,} \in \mathrm {Der}_{\mathbb {Q}[\mu ]}\left( \mathbb {Q}\Big [\frac {\,1}{\,\varDelta \,},\,\mu, \,x,\,y,\,\frac {1}{\,f_2(x,y)\,}\Big ]\,;\ \frac {\,\partial \,}{\partial \mu _j\,}\right). \end{align*}

Remark 2.15. (1) While operating $\ell _j$ on an element in $\mathbb {Q}[\mu, x,y]\frac {\,dx\,}{f_y}$ , some terms with ${f_y}^2$ in its denominators appear. But, it is seen by ( 2.11 ) or ( 2.14 ) that we have only terms with $f_y$ of 1st degree in their denominators modulo the exact forms.

(2) Moreover, operating $\frac {\partial }{\,\partial \mu _j\,}$ on an element in $\mathbb {Q}[\mu, x,y]\frac {\,dx\,}{f_y}$ , we may have the denominator with the discriminant $\varDelta$ besides $f_y$ because of ( 2.11 ) and the fact $\det ([T_{ij}])$ is $\varDelta$ times a rational.

(3) Eventually, we have a nice definition 3.2 of the 1st de Rham cohomology $H^1_{\mathrm {dR}}(\mathscr {C}/\mathbb {Q}[\mu ])$ and a good differential module structure on it. This makes a clear view of our application of the theory of the Gauss-Manin connection.

(4) One more advantage of the formula ( 2.11 ) is that it gives tremendously fast algorithm to compute many examples of the systems of heat equations satisfied by the sigma functions. Analysing such examples, the results in [28] are obtained.

We refer the reader to [28] on a proof of 2.1.

Here we note the following equality for the proof of the next lemma. Applying $\frac {\partial \,y}{\,\partial \mu _{eq-k}}$ to $f(x,y)=0$ , we have $f_y\,\frac {\partial \,y}{\,\partial \mu _{eq-k}}-M_k=0$ , so that

(2.15) \begin{equation} \frac {\partial \,y}{\,\partial \mu _{eq-k}}=\frac {\,M_k\,}{f_y}. \end{equation}

We give the following lemma, by which we understand (2.11) below more clearly is a special case of Lemma 1 in p.125 of [11] (proved by the uniqueness assertion in 2.1).

Lemma 2.17. Denote by $\frac {d}{\,dx\,}$ the derivation in $\mathrm {Der}_{\mathbb {Q}[\mu ]}(\mathbb {Q}(\mu, x,y);0)$ determined by the properties that $\frac {d\mu _k}{dx}=0$ for any $k\in \mathrm {wt}(\mu )$ and $\frac {d}{\,dx\,}x=1$ . Then for any $k\in \mathrm {wt}(\widetilde {\mu })$ , we have

\begin{align*} \frac {d}{\,dx\,}\frac {\partial y}{\,\partial \mu _k\,} =\frac {\partial }{\,\partial \mu _k\,}\frac {dy}{\,dx\,}. \end{align*}

Therefore, we have additionally

\begin{align*} \frac {d}{\,dx\,}\ell _j=\ell _j\frac {d}{\,dx\,} \end{align*}

as a map from $\mathbb {Q}(\mu, x,y)dx$ into itself.

Proof. This is exactly Lemma 2 in [11], p.125, which we can check by using (2.16) as follows. The left-hand side is

\begin{align*} \begin{aligned} \frac {\,\partial \,}{\,\partial \mu _k\,}\frac {\,dy\,}{\,dx\,} &=-\frac {\,\partial \,}{\,\partial \mu _k\,}\frac {\,f_x\,}{\,f_y\,} =-\frac {\,\frac {\,\partial f_x\,}{\,\partial \mu _k\,}\,}{\,f_y\,} +\frac {\,f_x\frac {\,\partial f_y\,}{\,\partial \mu _k\,}\,}{\,{f_y}^2\,}\\[3pt] &=-\frac {\,-(M_{eq-k})_x+f_{xy}\tfrac {\,\partial y\,}{\,\partial \mu _k\,}\,}{\,f_y\,} +\frac {\,f_x\cdot \big ({-}(M_{eq-k})_y+f_{yy}\frac {\,\partial y\,}{\,\partial \mu _k\,}\big )\,}{\,{f_y}^2\,}\\[3pt] &=-\frac {\,-(M_{eq-k})_x+f_{xy}\tfrac {\,M_{eq-k}\,}{\,f_y\,}\,}{\,f_y\,} +\frac {\,f_x\cdot \big ({-}(M_{eq-k})_y+f_{yy}\tfrac {\,M_{eq-k}\,}{\,f_y\,}\big )\,}{\,{f_y}^2\,}. \end{aligned} \end{align*}

On the other hand, we have

\begin{align*} \begin{aligned} \frac {\,d\,}{\,dx\,}\frac {\,\partial y\,}{\,\partial \mu _k\,} &=\frac {\,d\,}{\,dx\,}\frac {\,M_{eq-k}\,}{\,f_y\,} \ \ \ (\,\because \ 2.16)\\[3pt] &=\frac {\,(M_{eq-k})_x+(M_{eq-k})_y\frac {\,dy\,}{\,dx\,}\,}{\,f_y\,} -\frac {\,M_{eq-k}\big (f_{yx}+f_{yy}\frac {\,dy\,}{\,dx\,}\big )\,}{\,{f_y}^2\,}\\[3pt] &=\frac {\,(M_{eq-k})_x-(M_{eq-k})_y\frac {\,f_x\,}{\,f_y\,}\,}{\,f_y\,} -\frac {\,M_{eq-k}\big (f_{yx}-f_{yy}\frac {\,f_x\,}{\,f_y\,}\big )\,}{\,{f_y}^2\,}. \end{aligned} \end{align*}

These two coincide and the formula follows.

Remark 2.18. Thanks to 2.1, and

\begin{align*} \ell _j\bigg (d\bigg (\frac {h}{\,f_2\,}\bigg )\bigg ) =\ell _j\bigg (\frac {d}{\,dx\,}\bigg (\frac {h}{\,f_2\,}\bigg )\bigg )dx =\frac {d}{\,dx\,}\bigg (\ell _j\bigg (\frac {h}{\,f_2\,}\bigg )\bigg )dx =d\!\bigg (\ell _j\bigg (\frac {h}{\,f_2\,}\bigg )\bigg ) \end{align*}

for any $h\in \mathbb {Q}[\mu, x,y]$ by 2.16, we see that

(2.18) \begin{equation} \begin{aligned} \ell _j&\in \mathrm {Der}_{\mathbb {Q}[\mu ]}\left(\mathbb {Q}[\mu, \,x,\,y]\frac {dx}{\,f_y\,} +d\left(\mathbb {Q}[\,\mu, \,x,\,y]\frac {1}{\,f_y\,}\right);\,\ell _j\right) \ \ \text {and}\\[3pt] \ell _j&\in \mathrm {Der}_{\mathbb {Q}[\mu ]}\left( \left(\mathbb {Q}[\mu, \,x,\,y]\frac {dx}{\,f_y\,} +d\left(\mathbb {Q}[\,\mu, \,x,\,y]\frac {1}{\,f_y\,}\right);\,\ell _j\right)\Big / d\left(\mathbb {Q}[\,\mu, \,x,\,y]\frac {1}{\,f_y\,}\right) \right). \end{aligned} \end{equation}

While we use the same notation $\ell _j$ for elements in different sets above, it is supposed that there is no confusion.

Definition 2.20. For later use, we denote the Lie subalgebra generated by all the $\ell _j$ s over the ring $\mathbb {Q}[\mu ]$ in the Lie algebra obtained as the union of the above sets by $\boldsymbol {L}$ :

(2.21) \begin{equation} \boldsymbol {L}\subset \mathrm {Der}_{\mathbb {Q}[\mu ]}\left ( \mathbb {Q}[\mu, \,x,\,y]\frac {dx}{\,f_y\,} +d\,\bigg (\mathbb {Q}[\,\mu, \,x,\,y]\frac {1}{\,f_y\,}\bigg )\right ). \end{equation}

Remark 2.22. The inclusion above might be an equality.

3. de Rham cohomology etc

3.1. Differential forms of the first kind of the curve

Recall that any term of the sequence $w_1$ , $w_2$ , $\cdots$ , $w_g\in \mathrm {wgs}(e,q)$ in (1.14) is written as

\begin{align*} w_j=2g-1-a_je-b_jq, \end{align*}

with non-negative integers $a_j$ , $b_j$ . Using this notation, we define differential forms

(3.1) \begin{equation} \omega _{w_j}=\frac {x^{a_j}y^{b_j}}{f_2(x,y)}dx, \ \ \ (j=1, \ \cdots, \ g). \end{equation}

These are of the first kind (namely holomorphic everywhere on $\mathscr {C}$ ) and of weight $w_j$ .

3.2. Forms of the second kind and the first de Rham cohomology

In this paper, we should consider the curve $\mathscr {C}$ and other objects arising from $\mathscr {C}$ to be defined over the ring $\mathbb {Q}[{\mu }]$ ; in which the period matrix $\varOmega$ is exceptional as is explained later, and is defined over the field $\mathbb {C}$ of complex numbers.

Throughout this paper, we mean by the (differential) forms of the second kind all the forms without non-zero residue everywhere on $\mathscr {C}$ . Therefore we include in them the differential forms of the first kind. However, we mean by the differential forms of the third kind the forms having non-zero residue pole somewhere on $\mathscr {C}$ , on which we never assume that their order of such poles to be $1$ and that they does not contain any form of the second kind.

It is easy to see that the set of differential forms of the second kind on $\mathscr {C}$ with a pole only at $\infty$ is exactly

\begin{align*} \mathbb {Q}[\mu, x,y]\frac {dx}{\,f_2(x,y)\,}. \end{align*}

In concord with our principle that we shall treat our materials not over the fields $\mathbb {Q}(\mu )$ but over the ring $\mathbb {Q}[\mu ]$ , we have the following definition, thanks to the horizontal derivation formula 2.1 and 2.17.

Definition 3.2. We define the first de Rham cohomology of $\mathscr {C}$ over $\mathbb {Q}[\mu ]$ by

(3.3) \begin{equation} H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }]) =\frac {\mathbb {Q}[\mu, x,y]\frac {dx}{\,f_2(x,y)\,}+d\,\big (\mathbb {Q}[\mu, x,y] \frac {1}{\,f_2(x,y)\,}\big )} {d\,\big (\mathbb {Q}[\mu, x,y]\frac {1}{\,f_2(x,y)\,}\big )}. \end{equation}

We are never concerned with higher cohomologies in this paper. We have an important remark here.

Remark 3.4. In order to define the first de Rham cohomology over $\mathbb {Q}[\mu ]$ which endures for calculation for ‘horizontal’ differentiations, namely, for extensions of the elements in $\mathrm {Der}(\mathbb {Q}[\mu ])$ , the right-hand side of ( 3.3 ) is the ‘slimmest form’ as explained in the following. For an integer $k$ , we denote by $\omega _{\mathscr {C}}(k\cdot \infty )$ (resp. by $L_{\mathscr {C}}(k\cdot \infty )$ ) the module consists of the forms in $\mathbb {Q}[\mu, x,y]\frac {dx}{\,f_2(x,y)\,}$ (resp. the functions (the polynomials) in $\mathbb {Q}[\mu, x,y]$ ) whose order of the pole at $\infty$ is at most $k$ . Then we see by Theorem 8.2 in p.30 of [17] that

\begin{align*} H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }]) \simeq \frac {\,\omega _{\mathscr {C}}((2g-2)\cdot \infty )\,} {\,dL_{\mathscr {C}}((2g-1)\cdot \infty )\,}. \end{align*}

and this is a module of rank $2g$ over $\mathbb {Q}[\mu ]$ . We place emphasis on this that the derivatives $\ell _j$ s in ( 2.10 ) and the derivatives $L_j$ s which appear in ( 5.39 ) (and any elements in the Lie algebra generated by them) do not act on $\omega _{\mathscr {C}}((2g-2)\cdot \infty )$ but on the module $\mathbb {Q}[\mu, x,y]\frac {dx}{\,f_2(x,y)\,}+d\,\big (\mathbb {Q}[\mu, x,y] \frac {1}{\,f_2(x,y)\,}\big )$ in ( 3.3 ). So that the definition ( 3.3 ) is much suitable for explicit calculation on $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }])$ as a differential $\boldsymbol {L}$ -module, where $\boldsymbol {L}$ is defined in ( 2.21 ).

3.3. Symplectic inner product

We want to choose good $g$ differential forms $\eta _{-w_j}$ ( $j=g$ , $\cdots$ , $1$ ) of the second kind and of weight $-w_j$ such that the $2g$ forms consists of them and the forms of the first kind in (3.1) give rise to a symplectic basis of the space $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }])$ which is equipped with a natural symplectic inner product explained below. We denote $\boldsymbol {\omega }=(\omega _{w_1},\cdots, \omega _{w_g},\eta _{-w_g},\cdots, \eta _{-w_1})$ .

As before, $(x,y)$ is a generic point of $\mathscr {C}$ . It is known that the $\eta _{-w_j}$ s as well as the $\omega _{w_j}$ s are defined over $\mathbb {Q}[{\mu }]$ , namely, they are of the form $\frac {h(x,y)}{f_2(x,y)}dx$ with $h(x,y)\in \mathbb {Q}[{\mu },x,y]$ (see [27], [28]). We already defined in (1.12) that

\begin{align*} M(x,y)=\{\,x^iy^j\,|\,0\leq i\leq q-2, \ 0\leq j\leq e-2\,\}. \end{align*}

The set $\big \{\frac {h(x,y)}{f_2(x,y)}\,dx\,|\,h(x,y)\in M(x,y)\big \}$ forms a basis of $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }])$ as a $\mathbb {Q}[{\mu }]$ -module. Here we note that the order of pole of $x^{q-2}y^{e-2}$ at $\infty$ , which is the largest in $M(x,y)$ , is

\begin{align*} e(q-2)+q(e-2) = 2(e-1)(q-1)-2=2g-2, \end{align*}

and $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }])$ is a free $\mathbb {Q}[{\mu }]$ -module of rank $2g$ .

The space $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }])$ is equipped with the anti-symmetric inner product given by

\begin{align*} \omega \star \eta =\mathop {\mathrm {Res}}_{P=\infty } \left(\int _{\infty }^P\omega \right)\eta (P) \end{align*}

for any $\omega$ , $\eta \in H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }])$ . This is formally defined using the formal expansion with respect to a local parameter at $\infty$ (see [27], [28]), which is a formal interpretation of the product $\omega \star \eta ={\displaystyle \mathop {\mathrm {Res}}_{P\in \mathscr {C}^{\circ }}} \big (\int _{\infty }^P\omega \big )\eta (P)$ if we regard the $\mu _j$ s as complex numbers and $\mathscr {C}$ as a non-singular curve (i.e. a compact Riemann surface). Here $\mathscr {C}^{\circ }$ is the regular polygon obtained from the Riemann surface attached to the curve $\mathscr {C}$ with respect to the paths

(3.5) \begin{equation} \{\alpha _j,\,\beta _j\,|\,j=1,\cdots, g\} \end{equation}

which form a symplectic basis of the homology group $H_1(\mathscr {C},\mathbb {Z})$ as usual.

We choose $\eta _{-w_i}$ to satisfy the symplectic relations

(3.6) \begin{equation} \omega _{w_i}\star \omega _{w_j}=0, \ \ \eta _{-w_i}\star \eta _{-w_j}=0, \ \ \omega _{w_i}\star \eta _{-w_j}=-\eta _{-w_j}\star \omega _{w_i}=\delta _{ij}. \end{equation}

The choice of $\eta _{-w_j}$ is not unique but given by using so-called the fundamental $2$ -form of Klein. For a more concrete construction of these forms, we refer the reader to [27] (or to [28] for more detailed description). Especially, as a $\mathbb {Q}[{\mu }]$ -module, the $\omega _{w_j}$ s and $\eta _{-w_j}$ s form a basis of $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }])$ .

4. The sigma function

4.1. Materials for the construction of the sigma functions

In this section, we recall the definition of the natural generalisation of (0.2) for the general curve $\mathscr {C}$ , which is a function of $g$ variables $u={}^{t}{[u_{w_g} \ \cdots \ u_{w_1}]}$ with $w_j\in \mathrm {wgs}(e,q)$ and written as $\sigma (u)$ $=\sigma (u_{w_g},\cdots, u_{w_1})$ . It is called, analogously, the sigma function for $\mathscr {C}$ . To define it precisely, we need to introduce the Schur polynomial, period matrices, and others.

We use the classical notation of matrices concerning theta series, so our notation is transposed from the notation of [9]. Specifically, we will denote the period matrix of a curve as (4.2) whereas Buchstaber and Leykin’s papers use the transpose of this matrix. The other differences between their notation and ours will follow from this.

Letting $\boldsymbol {T}=\sum _{j=1}^gu_{w_j}T^{w_j}$ with an indeterminate $T$ , we define $\{p_k\}$ by $p_k=0$ for negative $k$ and

\begin{align*} \sum _{k=0}^{\infty }p_kT^k=\sum _{n=0}\frac {\boldsymbol {T}^n}{n!}. \end{align*}

Then we define $s(u)=s(u_{w_g},\cdots, u_{w_1})$ (see Section 4 in [24]) by

(4.1) \begin{equation} s(u)=\det (\mathop {[\ p_{w_{g+1-i}+j-g}\ ]}_{1\leq i\leq g,\ 1\leq j\leq g}). \end{equation}

This is the Schur polynomial corresponding to the sequence $(w_g,\cdots, w_1)$ .

From now on in this Section, we assume all the $\mu _j$ s are complex numbers and $\mathscr {C}$ is non-singular. The period matrices are defined by $\varOmega =\bigg [\ \begin{matrix} \omega ^{\prime} &\ \omega ^{\prime\prime} \\[3pt] \eta ^{\prime} &\ \eta ^{\prime\prime} \end{matrix}\ \bigg ]$ with

(4.2) \begin{equation} \begin{aligned} \omega ^{\prime} &=\bigg [\int _{\alpha _j}\!\omega _{w_{g-i+1}}\bigg ], \ \ \omega ^{\prime\prime}=\bigg [\int _{\beta _j}\!\omega _{w_{g-i+1}}\bigg ], \\[3pt] \eta ^{\prime} &=\bigg [\int _{\alpha _j}\!\eta _{-w_{g-i+1}}\bigg ], \ \ \eta ^{\prime\prime}=\bigg [\int _{\beta _j}\!\eta _{-w_{g-i+1}}\bigg ], \end{aligned} \end{equation}

where the $\eta _{-w_j}$ ’s are ones of (3.6) and $\alpha _i$ s and $\beta _j$ ’s are ones of (3.5). We introduce the $g$ -dimensional space $\mathbb {C}^g$ with coordinates

(4.3) \begin{equation} u={}^{t}{[u_{w_g} \ u_{w_{g-1}} \ \cdots \ u_{w_1}]} \end{equation}

for the domain on which the sigma function is defined. We define a lattice in this space by

(4.4) \begin{equation} \varLambda =\omega ^{\prime}\mathbb {Z}^g+\omega ^{\prime\prime}\mathbb {Z}^g. \end{equation}

For any $u\in \mathbb {C}^g$ , we define $u^{\prime}$ , $u^{\prime\prime}\in \mathbb {R}^g$ by $u=\omega ^{\prime}u^{\prime}+\omega ^{\prime\prime}u^{\prime\prime}$ . Likewise, for $\ell \in \varLambda$ , we write $\ell =\omega ^{\prime}\ell ^{\prime}+\omega ^{\prime\prime}\ell ^{\prime\prime}$ with $\ell ^{\prime}$ , $\ell ^{\prime\prime}\in \mathbb {Z}^g$ . In addition, we write ${\omega ^{\prime}}^{-1}{}^{t}{(\omega _{w_g},\,\cdots, \,\omega _{w_1})}= {}^{t}{(\hat {\omega }_1,\,\cdots, \,\hat {\omega }_g)}$ , ${\omega ^{\prime}}^{-1}\omega ^{\prime\prime}=\big [\tau _{ij}\big ]$ , and define (see [22], p.3.82 or [18], p43)

(4.5) \begin{equation} \delta _j=-\tfrac 12\tau _{jj} +\sum _{i=1}^g\int _{\alpha _i}\bigg (\int _{\infty }^{P}\hat {\omega }_j\bigg )\, \hat {\omega }_i(P),\ \ \ \delta ={\omega ^{\prime}}\,{}^{t}{[\delta _1 \ \cdots \ \delta _g]}\in \mathbb {C}^g. \end{equation}

Then we define the Riemann constant by $[\delta ^{\prime}\ \delta ^{\prime\prime}]$ . It is well-known that $\delta ^{\prime}$ , $\delta ^{\prime\prime}\in (\frac 12\mathbb {Z})^g$ for our curve. The $[\delta ^{\prime}\ \delta ^{\prime\prime}]$ can be taken independent of the values of $\mu _j$ s with a suitable choice of the paths of integrals in (4.5).

Using the above notation, we define a linear form $L(\, \ )$ on $\mathbb {C}^g\times \mathbb {C}^g$ by

(4.6) \begin{equation} L(u,v)={}^{t}{u}\,(\eta ^{\prime}v^{\prime}+\eta ^{\prime\prime}v^{\prime\prime}). \end{equation}

This is $\mathbb {C}$ -linear with respect to the first variable, and $\mathbb {R}$ -linear with respect to the second. Moreover, we define

(4.7) \begin{equation} \chi (\ell )=\exp \,\big (2\pi \boldsymbol {i}({}^{t}{\delta ^{\prime}}\ell ^{\prime\prime}-{}^{t}{\delta ^{\prime}}\ell ^{\prime} +\frac 12{}^{t}{\ell ^{\prime}}\ell ^{\prime\prime})\big )\in \{1,\,-1\} \end{equation}

for any $\ell \in \varLambda$ . Let

(4.8) \begin{equation} \kappa \,:\,\mathbb {C}^g\,\longmapsto \,\mathbb {C}^g/\varLambda \end{equation}

be the map given by modulo $\varLambda$ , and $\mathrm {Sym}^k\,\mathscr {C}$ be the $k$ -th symmetric product of $\mathscr {C}$ . Then we have the Abel-Jacobi mapping

(4.9) \begin{equation} \iota \,:\,\mathrm {Sym}^k\,\mathscr {C} \longrightarrow \ \mathbb {C}^g/\varLambda, \ \ \ (P_1,\,\cdots \!,\,P_k)\longmapsto \ \sum _{j=1}^k\bigg ( \int _{\infty }^{P_j}\omega _{w_g}, \,\cdots, \, \int _{\infty }^{P_j}\omega _{w_1} \bigg ), \end{equation}

whose image is denoted by $\Theta ^{[k]}$ . We denote $\Theta =\Theta ^{[g-1]}$ , which is called the standard theta divisor of the Jacobian variety $\mathbb {C}^g/\varLambda$ of $\mathscr {C}$ . For $k=1$ , the map $\iota$ is an isomorphism from $\mathscr {C}$ to $\Theta ^{[1]}$ , by which we frequently identify these two.

4.2. Weight revisited

In this subsection, we assume all $\mu _j$ s in (1.1) are complex numbers. We denote by $\mathscr {C}_{\mu }$ the curve given by (1.1) and assume it is non-singular, namely, we assume it gives a Riemann surface. Here, we shall extend the notion of the weight $\mathrm {wt}$ of (1.4) as follows. Firstly, we define the weight of $u_j$ , a coordinate of $u$ in (4.3), by

(4.10) \begin{equation} \mathrm {wt}(u_j)=j. \end{equation}

We explain below that this definition is consistent with the settings of weight so far. For a later use in (5.40) for instance, we prepare another notation

\begin{align*} \mathrm {wt}(u)=\{\,\mathrm {wt}(u_{w_j})\,|\,j=1,\,\cdots, \,g\,\}=\mathrm {wgs}(e,q), \end{align*}

too. Let $\varepsilon$ be an arbitrary non-zero complex number and $\mathscr {C}_{\varepsilon \mu }$ be the curve defined by (1.1) with every $\mu _j$ being replaced by $\varepsilon ^{-j}\mu _j$ . Then the map

\begin{align*} \boldsymbol {\varepsilon }\,:\, \mathscr {C}_{\mu }\longrightarrow \mathscr {C}_{\varepsilon \mu }, \ \ \ (x,y)\longmapsto (\varepsilon ^{-e}x, \varepsilon ^{-q}y) \end{align*}

is an isomorphism (i.e. an isomorphism of compact Riemann surfaces). Now we extend the defining domain of $\mathrm {wt}$ to the space $\mathbb {C}^g$ of (4.3) as follows. We take a fixed reference point $(\{{\mu _j}^{(0)}\},\,u^{(0)})$ of $(\mu, \,u)=(\{\mu _j\},\,u)$ of (1.1) and (4.3), and assume $\mathscr {C}_{\mu ^{(0)}}$ is also non-singular. Let

(4.11) \begin{equation} \mathscr {M}=\mathscr {M}(\mu ^{(0)},\,u^{(0)}) \end{equation}

be the germ of the analytic functions of $(\mu, \,u)$ at $(\mu ^{(0)},\,u^{(0)})$ , where we regard them as complex variables. Let $\varPhi (\mu, u)\in \mathscr {M}$ . We denote by $\varPhi (\varepsilon \mu, \varepsilon {u})$ the function obtained from $\varPhi (\mu, u)$ by replacing all $\mu _j$ by $\varepsilon ^{-j}\mu$ and all $u_i$ by $\varepsilon ^iu_i$ for $i=w_g$ , $\cdots$ , $w_1$ . We say that the function obtained is induced by the mapping $\boldsymbol {\varepsilon }$ . If there is a constant integer $w$ such that

\begin{align*} \varPhi (\varepsilon \mu, \varepsilon {u})=\varepsilon ^{w}\,\varPhi (\mu, {u}) \end{align*}

for any $\varepsilon \in \mathbb {C}$ , then we say the function $\varPhi (\mu, u)$ is of weight $w$ , and denote this as

\begin{align*} \mathrm {wt}(\varPhi (\mu, u))=w. \end{align*}

Now we explain that the definition of $\mathrm {wt}$ is actually an extension of the weight defined at (1.4). The coordinates $x$ and $y$ of $\mathscr {C}_{\mu }$ are naturally seen as functions of $u_g$ of $u$ in (4.3) on certain restricted domain in $\mathbb {C}^g$ for any $\mu _j\in \mathbb {C}$ , which should be denoted by $\kappa ^{-1}\iota (\mathscr {C})$ by using the notation (4.8) and (4.9). Then, observing the weight of $x$ and $y$ as power series of $u_g$ , their weights are $-e$ and $-q$ , respectively. The function $u_g\mapsto x$ above is seen as the restriction to $\kappa ^{-1}\iota (\mathscr {C})$ of the Abelian function

(4.12) \begin{equation} u\longmapsto \frac {x_1\cdots x_g} {\displaystyle \sum _{1\leq i_1\lt \cdots \lt i_{g-1}\leq g}\!\!\!\!\!x_{i_1}\cdots {}x_{i_{g-1}}}, \end{equation}

where $u=\iota ((x_1,y_1),\,\cdots, \,(x_g,y_g))\,\bmod {\varLambda }$ . The function (4.12) is easily checked to be of weight $-e$ . Under similar observation, the function $u_g\mapsto y$ is seen of weight $-q$ . Summarising the above, the notion of weight of (1.4) is completely compatible with the former notion above as well as one on $\mathscr {M}$ .

Take any circuit integrals of an entry of one of the matrices in (4.2) and consider the map $\boldsymbol {\varepsilon }$ . For example, we choose $\int _{\alpha _j}\omega _{w_i}$ . Note that it is an element in $\mathscr {M}$ which is a function on $\mu _j$ s and independent of $u$ . While the map $\boldsymbol {\varepsilon }$ changes $\omega _{w_i}$ to $\varepsilon ^{w_i}\omega _{w_i}$ as $\mathrm {wt}(\omega _{w_i})=w_i$ , the deformation of the path $\alpha _j$ of the integral no longer affects this change of value integral because of Cauchy’s theorem. So that, the mapping $\boldsymbol {\varepsilon }$ induces a change of the integral

\begin{align*} \int _{\alpha _j}\omega _{w_i} \longmapsto \ \varepsilon ^{w_i}\!\int _{\alpha _j}\omega _{w_i}, \end{align*}

for any non-zero $\varepsilon$ . Therefore, we have

\begin{align*} \mathrm {wt}\left(\,\int _{\alpha _j}\omega _{w_i}\right)=w_i. \end{align*}

By the argument above, the weight of such a circuit integral does not depend on its path of integral as well as the choice of the reference points ${\mu _j}^{(0)}$ s and $u^{(0)}$ . Because of (4.9) for $k=g$ is surjective (Jacobi’s theorem) and any values $\int _{\alpha _j}\omega _{w_i}$ s are appeared as the coordinates $u_{w_j}$ the definition of weight (4.10) is justified.

4.3. Construction of the sigma function

Using the notions defined in the previous subsections, we define the sigma function by the following characterisation. Now we fix the curve $\mathscr {C}=\mathscr {C}_{\mu }^{e,q}$ .

Theorem 4.13. There exists a unique function $(\mu, u)\mapsto \sigma (u)\,{=}\,\sigma (\mu, u)$ having the following properties:

1. (1) $\sigma (u)$ is an entire function on $\mathbb {C}^g$ for any fixed $\mu _j$ s in $\mathbb {C}$ ;

2. (2) Supposing that the $\{\mu _j\}$ are constants in $\mathbb {C}$ and the discriminant $\varDelta$ is not zero, we have

   \begin{align*} \sigma (u+\ell )=\chi (\ell )\,\sigma (u)\exp \,L(u+\tfrac 12\ell, \ell ) \ \ \ (u\in \mathbb {C}^g, \ \ell \in \varLambda ), \end{align*}
   where $\varLambda$ , $L$ , and $\chi$ are those of ( 4.4 ), ( 4.6 ), and ( 4.7 ), respectively ;

3. (3) Viewing $\sigma (u)$ as an element in $\mathscr {M}$ of ( 4.11 ) with an arbitrary reference point

   \begin{align*} \mathrm {wt}(\sigma (u))=\tfrac 1{24}{(e^2-1)(q^2-1)};\, \end{align*}
   Moreover, $\sigma (u)$ is expanded as a power series around the origin $(0,\cdots, 0)$ with coefficients in $\mathbb {Q}[{\mu }]$ , and is of homogeneous weight $(e^2-1)(q^2-1)/24$ ;

4. (4) $\sigma (u)|_{{\mu }=\boldsymbol {0}}$ is the Schur polynomial $s(u)$ of ( 4.1 );

5. (5) $\sigma (u)=0$ $\iff$ $u\in \kappa ^{-1}(\Theta )$ .

Definition 4.14. We call the function $\sigma (u)$ whose existence is guaranteed by 4.1 the sigma function of the curve $\mathscr {C}$ .

The theorem 4.1 was proved in various ways in the literature, each version has a slightly different point of view. It is convenient to summarise here these versions from our point of view. We define

(4.15) \begin{equation} \begin{aligned} \tilde {\sigma }(u)&=\tilde {\sigma }(u,\varOmega ) =\left(\frac {(2\pi )^g}{\mathrm {det}\,{\omega ^{\prime}}}\right)^{\tfrac 12} \exp \big ({-}\tfrac 12\,{}^{t}{u}\,\eta ^{\prime}{\omega ^{\prime}}^{-1}u\big )\\[3pt] &\cdot \sum _{n\in \mathbb {Z}^g} \exp \big (\tfrac 12\,{}^{t}{(n+\delta ^{\prime\prime})}\,{\omega ^{\prime}}^{-1}\omega ^{\prime\prime}(n+\delta ^{\prime\prime}) +{}^{t}{(n+\delta ^{\prime\prime})}({\omega ^{\prime}}^{-1}u+\delta ^{\prime})\big ), \end{aligned} \end{equation}

where $\mathrm {det}$ denotes the determinant. Note that the arguments in any exponential are of weight $0$ , so that the infinite series part of (4.15) is of weight $0$ as well. It is easy to show that this function has property (1) (see 5.21 below) and that this function satisfies (2) using (5.3) below. Frobenius’ method shows that the solutions of the equation (2) form a one dimensional space (see p.93 of [17]). Although this function is constructed by using $\varOmega$ , it is independent of $\varOmega$ . Namely, the function $\tilde {\sigma }(u,\varOmega )$ is invariant under a modular transform, that is the transform of $\varOmega$ by $\mathrm {Sp}(2g,\mathbb {Z})$ which come from changing the choice of $\alpha _i$ s and $\beta _i$ s. Therefore, it is expressed as a power series of $u$ with coefficients being functions of only the $\mu _j$ s. On the latter part of (3) and (4), we refer the reader to [24]. In that paper, $\tilde {\sigma }(u)$ times some constant is expressed as a determinant of infinite size (see also [27]). See also the paper [23] by Nakayashiki, in which he proved the sigma function is no other than (4.15) times a non-zero constant depending on $\mu _j$ s with emphasising the later part of (3). That $\tilde {\sigma }(u)$ has the property (5) come from a well-known property of Riemann theta function. Using notation we have explained previously, we define

(4.16) \begin{equation} \hat {\sigma }(u)=\varDelta ^{-\frac 18}\tilde {\sigma }(u), \end{equation}

with an appropriate choice of the $\frac 18$ th root of the discriminant $\varDelta$ . It is known for $g=1$ and $2$ that this function exactly satisfies all the properties in 4.1, namely, we have $\sigma (u)=\hat {\sigma }(u)$ . For $g=1$ , it is shown as in [26] by a transformation formulae for $\eta (\tau )$ and the theta series described in pp.176–180 of [29], and for $g=2$ the paper [16] by D. Grant, in which the property (4) is shown by using Thomae’s formula.

However, it is not known for $g\geq 3$ if the function (4.16) is really the sigma function. The paper [9] is the first one to seriously attack this problem.

In this paper, we show, following the idea of [9], that $\sigma (u)=\hat {\sigma }(u)$ for the genus $3$ curves that is for the $(2,7)$ -curve and the $(3,4)$ -curve. This means (4.16) satisfies especially (4) up to an absolutely numerical multiplicative constant. The strategy of the proof is as follows: We construct a system of linear partial differential equations (heat equations) satisfied by $\hat {\sigma }(u)$ and show that the solution space is of dimension one (over the base field) by explicit construction of a recursive system for the coefficients of the power series expansion of any unknown solution and showing the uniqueness of the solution of this system. Then we see $\sigma (u)=\hat {\sigma }(u)$ up to a non-zero multiplicative absolutely numerical constant. This result might be seen as a generalisation of Thomae’s formula ( [30]). Section 6 is devoted to these last steps.

5. Theory of heat equations

5.1. Generalisation of the frobenius-stickelberger theory

This and the following sections are devoted to explaining the theory of Buchstaber and Leykin [9], on the differentiation of Abelian functions with respect to their parameters, as clearly as we can. That generalises the work of Frobenius and Stickelberger [14], discussed above, on the elliptic function case of this problem.

For higher genus cases, we do not have a naive generalisation of (0.8) and (0.9), which are mentioned in the Introduction. However, we can give a natural generalisation of the relations (0.10) to the curve $\mathscr {C}_{\mu }$ as explained in the next section.

As we discussed in Subsection 3.2, any element $L$ in $\boldsymbol {L}$ of (2.21) operates linearly on the space $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[\mu ])$ . For complex variables $\mu _j$ s, we let $L$ operate firstly on the forms with variables $\mu _j$ s of representative of basis of $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[\mu ])$ , then we restore $\mu _j$ s to the original values in $\mathbb {C}$ .

Taking a derivative $L\in \boldsymbol {L}$ , we define $\Gamma ^L\in \mathrm {Mat}(2g,\mathbb {Q}[{\mu }])$ as the representation matrix of the action of $L$ by

(5.1) \begin{equation} L(\boldsymbol {\omega })=\boldsymbol {\omega }\,{}^{t}{\Gamma ^L} \ \ \ \textrm {for} \ \ \boldsymbol {\omega }=(\omega _{w_g},\,\cdots, \,\omega _{w_1},\,\eta _{-w_g},\,\cdots, \,\eta _{-w_1}) \in H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }]). \end{equation}

In [9], the matrix $-\!{}^{t}(\Gamma ^L)$ defined by (5.1) is called the Gauss-Manin connection for the derivation (vector field) $L$ .

From here to the end of Section 5, we assume that all the $\mu _j$ s are complex variables which vary as $\mathscr {C}$ is non-singular. We can then use the periods $\omega _{ij}$ s and $\eta _{ij}$ s.

By integrating (5.1) along each element in the chosen symplectic basis of $H_1(\mathscr {C},\,\mathbb {Z})$ , we get the natural action

(5.2) \begin{equation} L(\varOmega )=\Gamma ^L\,\varOmega \end{equation}

of $L$ on the space of $\varOmega$ s for all the choices of symplectic basis of $H_1(\mathscr {C},\,\mathbb {Z})$ . So, we see also how $L$ operates on the field $\mathbb {Q}(\{{\omega ^{\prime}}_{ij}\},\,\{{\omega ^{\prime\prime}}_{ij}\})$ . Of course, since $\varOmega$ is the period matrix of a symplectic basis, these elements must satisfy the constraint

(5.3) \begin{equation} {}^{t}{\varOmega } J \varOmega = 2 \pi i J, \ \ \ \textrm {where} J=\bigg [\begin{matrix} & 1_g\\[3pt] -1_g & \end{matrix}\bigg ] \end{equation}

by (3.6). This is none other than the generalisation of Frobenius-Stickelberger’s relation (0.10) and is to say that $(2\pi {i})^{-\frac 12}\varOmega \in \mathrm {Sp}(2g,\mathbb {C})$ . It follows immediately that

(5.4) \begin{equation} \varOmega ^{-1} =\frac {1}{2\pi i}J^{-1}\, {}^{t}{\varOmega }J =\frac {1}{2\pi i} \bigg [ \begin{array}{r@{\quad}r} {}^{t}{\eta ^{\prime\prime}} &\ -{}^{t}{\omega ^{\prime\prime}}\\[3pt] -{}^{t}{\eta ^{\prime}} & {}^{t}{\omega ^{\prime}} \end{array} \bigg ]. \end{equation}

After operating $L$ on both sides of (5.3), using (5.2) and (5.3), we see that the matrix $\Gamma ^L$ satisfies

(5.5) \begin{equation} {}^{t}\Gamma ^LJ + J \Gamma ^L = 0, \ \ \textrm {i.e.}\ \ {}^{t}{(\Gamma ^LJ)}=\Gamma ^LJ \end{equation}

because $L({}^{t}{\varOmega })={}^{t}{\varOmega }\,{}^{t}{\Gamma ^L}$ , which is to say that $\Gamma ^L$ is in the Lie algebra $\mathfrak {sp}(2g,\mathbb {Q}[\mu ])$ of $\mathrm {Sp}(2g,\mathbb {Q}[\mu ])$ . Thus we may write

(5.6) \begin{equation} -\Gamma ^LJ=\bigg [\, \begin{matrix} \alpha & \ \beta \\[3pt] {}^{t}{\beta }& \ \gamma \end{matrix}\, \bigg ], \ \ \ \Gamma ^L = \bigg [ \begin{array}{c@{\quad}r} -\beta & \ \alpha \\[3pt] -\gamma & {}^{t}{\beta } \end{array} \bigg ] \end{equation}

with ${}^{t}{\alpha }=\alpha$ and ${}^{t}{\gamma }=\gamma$ .

Remark 5.7. (1) We use a different notation for $D(x,y,\lambda )$ compared to p.273 of [9], and for $\Omega$ , $\Gamma$ and $\beta$ compared to p.274 of loc. cit. Our ${}^{t}{\boldsymbol {\omega }}$ equals $D(x,y,\lambda )$ by transposing and changing the sign on the latter half entries. The others are naturally modified according to this difference and taking transposes. We will give a detailed comparison of our notation with theirs in 5.57 at the end of Subsection 5.6. (2) In general, it requires some work to write down the given operator $L$ as a partial differential operator with respect to the periods ${\omega ^{\prime}}_{ij}$ and ${\omega ^{\prime\prime}}_{ij}$ similar to the LHS of ( 0.10 ). However, we do not use such an expression in the present paper.

Conversely, starting from a matrix

\begin{align*} \Gamma = \bigg [ \begin{array}{c@{\quad}r} -\beta & \ \alpha \\[3pt] -\gamma & {}^{t}{\beta } \end{array} \bigg ]\in \mathfrak {sp}(2g,\mathbb {Q}[{\mu }]), \end{align*}

with ${}^{t}{\alpha }=\alpha$ and ${}^{t}{\gamma }=\gamma$ , we get uniquely an operator $L\in \boldsymbol {L}$ such that $\Gamma ^L=\Gamma$ . So far, this is a natural generalisation of the situation investigated by Frobenius-Stickelberger [14].

5.2. The primary heat equation

In this Section, we review the general heat equations satisfied by the sigma functions.

If we want to find second-order linear partial differential equations (heat equations) satisfied by the sigma function, we should proceed in as general a way as possible. Here, note that the equation (0.6) is satisfied not only by the Jacobi theta function (0.3) but also by each individual term of the sum in (0.3). This corresponds a statement in the proof of Theorem 13 in page 274 of [9]. Here we will review their theory of such equations, correcting a few minor errors, and apply it explicitly to more general curves than considered in [9]. We shall start from this point of view.

Take an derivative $L\in \boldsymbol {L}$ and assume it is of homogeneous weight, say $\mathrm {wt}(L)=k$ (see (2.7)), we have the symmetric matrix $-\Gamma ^L J= \bigg [\, \begin{matrix} \alpha & \beta \\[3pt] {}^{t}{\beta }& \gamma \end{matrix}\, \bigg ]$ with

\begin{align*} \alpha =\underset {\substack {i\in \mathrm {wt}(u)\\[3pt] j\in \mathrm {wt}(u)}}{[\alpha _{-i,k-j}]}, \ \ \beta =\underset {\substack {i\in \mathrm {wt}(u)\\[3pt] j\in \mathrm {wt}(u)}}{[\beta _{j,k-i}]}, \ \ \gamma =\underset {\substack {i\in \mathrm {wt}(u)\\[3pt] j\in \mathrm {wt}(u)}}{[\gamma _{-i,k+j}]} \end{align*}

and we also associate with it a second-order differential operator $H^L$ , given by

(5.8) \begin{equation} \begin{aligned} H^L&=\frac 12[\,{}^{t}{\partial _u}\ {}^{t}{u}\,] \bigg [ \begin{array}{r@{\quad}c} \alpha & \ \beta \\[3pt] {}^{t}{\beta } & \ \gamma \end{array} \bigg ] \bigg [ \begin{array}{c} \partial _u \\[3pt] u \end{array} \bigg ]\\[3pt] &=\sum _{i\in \mathrm {wt}(u)}\sum _{j\in \mathrm {wt}(u)} \left(\tfrac 12\,{\alpha }_{-i,\,k-j}\ \frac {\partial ^2}{\partial u_i\partial u_j} +{\beta }_{-j,\,k-i}\ u_i\frac {\partial }{\partial u_j} +\tfrac 12\,{\gamma }_{-i,\,k+j}\ u_iu_j\right) +\tfrac 12\,{\mathrm {Tr}\,\beta }. \end{aligned} \end{equation}

Here $\partial _u$ denotes the column vector with $g$ components $\frac {\partial }{\partial u_i}$ , and $u$ the column vector with $g$ components $u_i$ s. The very last term comes from the commutation relation $\tfrac {\partial }{\partial u_i}u_j=u_j\tfrac {\partial }{\partial u_i}+\delta _{ij}$ . It is then straightforward to verify the following

Lemma 5.9. If we define a function $G_0(u,\varOmega )$ (this is a Green’s function) by

\begin{align*} G_0(u,\varOmega ) =\left(\frac {(2\pi )^g}{\mathrm {det}\,\omega ^{\prime}}\right)^{\frac 12} \exp \big ({-}\tfrac 12\,{}^{t}{u}\,\eta ^{\prime}{\omega ^{\prime}}^{-1}u\big ), \end{align*}

then the following equation (a heat equation ) holds :

(5.10) \begin{equation} (L - H^L) G_0 =0. \end{equation}

Proof. We have

(5.11) \begin{equation} \begin{aligned} L\,G_0 &=-\frac 12 \mathrm {Tr}(\omega ^{\prime-1} L(\omega ^{\prime}))G_0 -\frac 12 ({}^{t}{u}\,L(\eta ^{\prime}){\omega ^{\prime}}^{-1}u)G_0 +\frac 12 ({}^{t}{u}\,\eta ^{\prime}{\omega ^{\prime}}^{-1}L(\omega ^{\prime}){\omega ^{\prime}}^{-1}u)G_0\\[3pt] &=\frac 12\left [\mathrm {Tr}(\omega ^{\prime-1}(\beta \omega ^{\prime} - \alpha \eta ^{\prime})) +({}^{t}{u}\,((\gamma \omega ^{\prime} - {}^{t}{\beta } \eta ^{\prime})\omega ^{\prime-1} -\eta ^{\prime}{\omega ^{\prime}}^{-1}(\beta \omega ^{\prime} - \alpha \eta ^{\prime})\omega ^{\prime-1}) \,u)\right ]G_0\\[3pt] &=\frac 12\left [\mathrm {Tr}(\beta -\alpha \eta ^{\prime} \omega ^{\prime-1}) + ({}^{t}{u}\,(\gamma -{}^{t}{\beta }\eta ^{\prime}{\omega ^{\prime}}^{-1} -\eta ^{\prime}{\omega ^{\prime}}^{-1}\beta +\eta ^{\prime}{\omega ^{\prime}}^{-1}\alpha \eta ^{\prime}{\omega ^{\prime}}^{-1})\,u) \right ]G_0 \end{aligned} \end{equation}

by using

(5.12) \begin{equation} L(\varOmega )=\Gamma ^L \varOmega =\bigg [ \begin{array}{r@{\quad}r} -\beta & \ \alpha \\[3pt] -\gamma & {}^{t}{\beta } \end{array} \bigg ] \bigg [ \begin{array}{r@{\quad}r} \omega ^{\prime} & \ \omega ^{\prime\prime} \\[3pt] \eta ^{\prime} & \ \eta ^{\prime\prime} \end{array} \bigg ] =\bigg [ \begin{array}{c@{\quad}c} -\beta \omega ^{\prime}+\alpha \eta ^{\prime} & -\beta \omega ^{\prime\prime}+\alpha \eta ^{\prime\prime} \\[3pt] -\gamma \omega ^{\prime} +{}^{t}{\beta }\eta ^{\prime} & -\gamma \omega ^{\prime\prime} +{}^{t}{\beta } \eta ^{\prime\prime} \end{array} \bigg ]. \end{equation}

The result of (5.11) coincides with that of

\begin{align*} \begin{aligned} H^{L_0}G_0 &= \frac 12 \big [{}^{t}{\partial _u}\ {}^{t}{u}\big ] \bigg [\, \begin{matrix} \alpha & \ \beta \\[3pt] {}^{t}{\beta } & \ \gamma \end{matrix}\, \bigg ] \bigg [ \begin{matrix} \partial _u \\[3pt] u \end{matrix} \bigg ]G_0 =\frac 12 \big [{}^{t}{\partial _u} \ {}^{t}{u}\big ] \bigg [\, \begin{matrix} \alpha & \ \beta \\[3pt] {}^{t}{\beta } & \ \gamma \end{matrix}\, \bigg ] \bigg [\, \begin{matrix} -\eta ^{\prime}\omega ^{\prime-1}u \\[3pt] u \end{matrix}\, \bigg ]G_0 \\[3pt] &=\frac 12 \mathrm {Tr}({}^{t}{\beta } -\alpha \eta ^{\prime} \omega ^{\prime-1})\,G_0 +\frac 12 \big [{-}{}^{t}{u}\eta ^{\prime} \omega ^{\prime-1} \ \ u \,\big ] \bigg [ \begin{array}{r@{\quad}r} \alpha & \ \beta \\[3pt] {}^{t}{\beta } & \ \gamma \end{array} \bigg ] \bigg [\, \begin{matrix} -\eta ^{\prime}\omega ^{\prime-1}u \\[3pt] u \end{matrix}\, \bigg ]G_0. \end{aligned} \end{align*}

Here we have used the generalised Legendre relation (5.3) and the symmetry of $\eta ^{\prime} \omega ^{\prime-1}$ .

Now we recall that the different terms in the expansion of the theta function are periodic translates of one another. Analogously, to construct the different terms appearing in the expansion of the sigma function, we act on $G_0$ by iterating an element of the Heisenberg group. For a variable $z\in \mathbb {Q}(\{{\omega ^{\prime}}_{ij}\},\,\{{\omega ^{\prime\prime}}_{ij}\})$ , and a two $g$ -component column vectors $p$ , $q$ whose components also belong to $\mathbb {Q}(\{{\omega ^{\prime}}_{ij}\},\,\{{\omega ^{\prime\prime}}_{ij}\})$ , we introduce

\begin{align*} F(z,p,q)=\exp (z)\exp ({}^{t}{p}u)\exp ({}^{t}{q}\partial _u). \end{align*}

We write its inverse operator as

\begin{align*} F^{-1}(z,p,q)=\exp ({-}{}^{t}{q}\partial _u)\exp ({-}{}^{t}{p}u)\exp ({-}z). \end{align*}

Lemma 5.13. Defining $F(z,p,q)$ for any $p$ , $q$ and $z$ , and $H^L$ for $L\in \boldsymbol {L}$ as in ( 5.8 ), the operator equality

(5.14) \begin{equation} F^{-1}(z,p,q)(L - H^L)F(z,p,q)=L - H^L \end{equation}

holds if and only if

(5.15) \begin{equation} L \bigg [\, \begin{matrix} q \\[3pt] p \end{matrix}\, \bigg ] =\Gamma ^L \bigg [\, \begin{matrix} q \\[3pt] p \end{matrix}\, \bigg ] \ \ \textrm {and} \ \ L(z)=\frac 12\,(\,{}^{t}{p}\alpha p - {}^{t}{q}\gamma q\,). \end{equation}

Here $\Gamma ^L$ is that of ( 5.6 ).

Proof. We calculate directly that

\begin{align*} \begin{aligned} F^{-1}(z,p,q)\,LF(z,p,q) &=F^{-1}(z,p,q) \big (\,L(z) +L({}^{t}{p})\,u+L({}^{t}{q}) \,\partial _u\,\big ) F(z,p,q)+L \\[3pt] &=L+ \big (\, L(z) +L({}^{t}{p})(u-q)+L({}^{t}{q})\,\partial _u\,\big ). \end{aligned} \end{align*}

Similarly, we find

\begin{align*} \begin{aligned} F^{-1}(z,p,q)&\,H^LF(z,p,q) =\frac 12 \big [{}^{t}{\partial _u}+{}^{t}{p} \ {}^{t}{u}-{}^{t}{q}\big ] \bigg [\, \begin{matrix} \alpha & \beta \\[3pt] {}^{t}{\beta }& \gamma \end{matrix}\, \bigg ] \bigg [\, \begin{matrix} \partial _u+p \\[3pt] u-q \end{matrix}\, \bigg ] \\[3pt] &=H^L +\big [{}^{t}{p}\ \ -{}^{t}{q}\big ] \bigg [\, \begin{matrix} \alpha & \beta \\[3pt] {}^{t}{\beta } & \gamma \end{matrix}\, \bigg ] \bigg [\, \begin{matrix} \partial _u \\[3pt] u \end{matrix}\, \bigg ] +\frac 12\big [{}^{t}{p}\ \ -{}^{t}{q}\big ] \bigg [\, \begin{matrix} \alpha & \beta \\[3pt] {}^{t}{\beta } &\gamma \end{matrix}\, \bigg ] \bigg [ \begin{matrix} p \\[3pt] -q \end{matrix} \bigg ]. \end{aligned} \end{align*}

Matching coefficients of $\partial _u$ , $u$ , and $1$ , and transposing and rearranging, we see that, respectively,

\begin{align*} L(q)=[{-}\beta \ \ \alpha \,] \bigg [\, \begin{matrix} q \\[3pt] p \end{matrix}\, \bigg ], \ \ \ L(p)=[\,-\gamma \ {}^{t}{\beta }\,] \bigg [\,\begin{matrix} q \\[3pt] p \end{matrix}\,\bigg ], \ \ \ L(z)=\frac 12\,(\,{}^{t}{p}\alpha p - {}^{t}{q}\gamma q\,) \end{align*}

as desired.

Corollary 5.16. The formula ( 5.15 ) holds if

(5.17) \begin{equation} \bigg [\, \begin{matrix} q \\[3pt] p \end{matrix}\, \bigg ] =\varOmega \bigg [ \begin{matrix} b^{\prime} \\[3pt] b^{\prime\prime} \end{matrix} \bigg ], \ \ z = z_0 + \tfrac 12{}^{t}{p}q, \end{equation}

where $b^{\prime}$ and $b^{\prime\prime}$ are arbitrary numerical constant vectors, and $z_0$ is an irrelevant numerical constant, which we set to zero below.

Proof. We have $L\left( \bigg [ \begin{matrix} q \\[3pt] p \end{matrix} \bigg ]\right) =L(\Omega ) \bigg [ \begin{matrix} b^{\prime} \\[3pt] b^{\prime\prime} \end{matrix} \bigg ] =\Gamma ^L\Omega \bigg [ \begin{matrix} b^{\prime} \\[3pt] b^{\prime\prime} \end{matrix} \bigg ] =\Gamma ^L \bigg [ \begin{matrix} p \\[3pt] q \end{matrix} \bigg ]$ , which is the former relation in (5.15). The latter one is checked easily.

Denoting the constant vector ${}^{t}{[b^{\prime}\ b^{\prime\prime}]}$ simply by $b$ , we denote $p$ , $q$ , and $z$ with $z_0=0$ in (5.17) by $p(b)$ , $q(b)$ , and $z(b)$ , respectively. We define

\begin{align*} G(b,u,\varOmega )=F\big (z(b),p(b),q(b)\big )\,G_0(u,\varOmega ). \end{align*}

Using the Legendre relation (5.4), we note that ${}^{t}{p}\omega ^{\prime}-{}^{t}{q}\eta ^{\prime}= 2\pi i {}^{t}{b^{\prime\prime}}$ , and hence we obtain

\begin{align*} \begin{aligned} G&(b,u,\varOmega ) = F\big (z(b),p(b),q(b)\big )\,G_0(u,\varOmega )\\[3pt] &=\exp (\tfrac 12 {}^{t}{p}q)\,\exp ({}^{t}{p}u)\,\exp ({-}{}^{t}{q}\eta ^{\prime}\omega ^{\prime-1}u) \exp ({-}\tfrac 12 {}^{t}{q}\eta ^{\prime} \omega ^{\prime-1}q)\,G_0\\[3pt] &= \exp ({-}\tfrac 12 (2\pi i {}^{t}{b^{\prime\prime}} \omega ^{\prime-1}q) \exp (2\pi i {}^{t}{b}^{\prime\prime} \omega ^{\prime-1}u)\,G_0\\[3pt] &= \exp ({-}\tfrac 12 (2\pi i {}^{t}{b^{\prime\prime}} \omega ^{\prime-1}(\omega ^{\prime} b^{\prime} +\omega ^{\prime\prime}b^{\prime\prime}) \exp (2\pi i {}^{t}{b}^{\prime\prime} \omega ^{\prime-1}u)\,G_0 \\[3pt] &=\bigg (\frac {(2\pi )^g}{\mathrm {det}(\omega ^{\prime})}\bigg )^{\frac 12}\, \exp \big ({-}\tfrac 12 {}^{t}{u}\eta ^{\prime} \omega ^{\prime-1} u\big ) \,\exp \left(\,2\pi i\big (\,\tfrac 12 {}^{t}{b^{\prime\prime}} \omega ^{\prime-1} \omega ^{\prime\prime} b^{\prime\prime}+ {}^{t}{b^{\prime\prime}}(\omega ^{\prime-1}u+b^{\prime})\,\big )\right). \end{aligned} \end{align*}

Now, the following theorem, which is the foundation of BL theory, is obvious from (5.10) and (5.14).

Theorem 5.18. (The primary heat equation) For the function $G(b,u,\varOmega )$ above, one has

(5.19) \begin{equation} (L-H^L)\,G(b,u,\varOmega )=0 \end{equation}

for any $L\in \boldsymbol {L}$ .

5.3. The algebraic heat operators

For the coordinates of the space in which the sigma function is defined, we do not use $(u_1,\cdots, u_g)$ for subscripts of the variable $u$ , but denote instead, as in (4.3)

\begin{align*} u=(u_{w_g},\cdots, u_{w_1}). \end{align*}

That is, the components of $u$ are labelled by their weights, which are the Weierstrass gaps. $\Gamma ^L\in \mathfrak {sp} (2g,\mathbb {Q}[\mu ])$ . As a corollary to Theorem 5.1, we have

Corollary 5.20. Let

(5.21) \begin{equation} \rho (u)=\sum _{b}c_b\,G(b,u,\varOmega ), \end{equation}

where $b$ runs through the elements of any set $\subset$ $\mathbb {C}^{2g}$ and $c_b\in \mathbb {C}$ are constants such that the sum converges absolutely. Then we have, for any $L\in \boldsymbol {L}$ , that

\begin{align*} (L-H^L)\,\rho (u,\varOmega )=0. \end{align*}

Proof. Since both of $L$ and $H^L$ are independent of $b$ , each term of $\rho (u)$ satisfies (5.19).

Remark 5.22. Assume that $\mathscr {C}_{{\mu }}$ is non-singular. Let $\varOmega$ be the usual period matrix defined by ( 4.2 ), and $\delta$ be its Riemann constant. The function defined at ( 4.15 ) is written as

(5.23) \begin{equation} \tilde {\sigma }(u)=\tilde {\sigma }(u,\varOmega ) =\sum _{n\in \mathbb {Z}^g}G( {}^{t}{[ \delta ^{\prime}\ n+\delta ^{\prime\prime}]},u,\varOmega ). \end{equation}

Since the imaginary part of $\omega ^{\prime-1}\omega ^{\prime\prime}$ is positive definite, this series converges absolutely. This is a special case of $\rho (u)$ of ( 5.19 ).

Because both $L$ and $H^L$ are independent of $b$ , there are infinitely many linearly independent entire functions $\rho (u)$ on $\mathbb {C}^g$ satisfying $(L-H^L)\rho (u)=0$ . Moreover, since, for a fixed $b$ , the function $G(b,u,\varOmega )$ is independent of $L$ , we see that, by switching the choice of $L$ , there are infinitely many linearly independent operators of the form $(L-H^L)$ which satisfy $(L-H^L)\,\rho (u)=0$ for some fixed $\rho (u)$ .

However, because our aim is to find a method to calculate the power series expansion of the sigma function, we need a more detailed discussion. For our purpose, we require

1. (A1) for any (or any element of good generators) $L\in \boldsymbol {L}$ find a good mapping which associates $L$ to a (quadratic linear differential) operator which annihilate the sigma function (4.16) as an element in the ring $\mathbb {Q}[{\mu }][[u]]$ , and

2. (A2) to show that the sigma function and its absolute constant multiples are exactly the functions in $\mathbb {Q}[{\mu }][[u]]$ killed by the operators obtained in (A1)

Since $L$ is a derivation with respect to the $\mu _j$ s but $H^L$ is a differential operator with respect to the $u_{w_j}$ s, we see that, for some function $\varXi$ depending only on the $\mu _j$ s,

\begin{align*} L\,\varXi \tilde {\sigma }(u) =(L\varXi )\,\tilde {\sigma }(u)+\varXi (L\tilde {\sigma }(u)),\ \ \ \ H^L\,\varXi \tilde {\sigma }(u) =\varXi (H^L\tilde {\sigma }(u)). \end{align*}

Therefore, $\varXi \tilde {\sigma }(u)$ satisfies

(5.24) \begin{equation} (L-H^L)(\varXi \tilde {\sigma }(u)) =\tfrac {L\varXi }{\varXi }\,\varXi \,\tilde {\sigma }(u) =(L\log \varXi )\varXi \,\tilde {\sigma }(u). \end{equation}

If $\varXi \,\tilde {\sigma }(u)$ is the correct sigma function, the left-hand side of the above is in $\mathbb {Q}[\mu ][[u]]$ , So, in order to get the function $\hat {\sigma }(u)$ of (4.16), $L\log \varDelta \in \mathbb {Q}[\mu ]$ . We shall show that this indeed holds for any $L\in \boldsymbol {L}$ in the next section.

5.4. The matrix $V$

Throughout this section, we suppose that all the $\mu _j$ ’s, $x$ , and $y$ are variables or indeterminates. In view of the approach in [9], we require that $L\log \varDelta$ belongs to $\mathbb {Q}[{\mu }]$ because of conditions (A1), (A2) and equation (5.24). We also explain suitable choices for $\Gamma$ for which $L$ satisfies the condition.

Now we explain another method, known in singularity theory, to calculate the discriminant $\varDelta$ and a basis of the space of the vector fields tangent to the variety defined by $\varDelta =0$ .

Let $(x,y)$ and $(z,w)$ are different generic points of $\mathscr {C}$ . Following p.112 of [8], we define a function $\mathrm {ph}\big ((x,y),(z,w)\big )$ (pre-hessian), which is defined by

\begin{align*} \mathrm {ph}\big ((x,y),(z,w)\big ) =\frac 12\left |\, \begin{matrix} \dfrac {f_1(x,y)-f_1(z,w)}{x-z} & \dfrac {f_2(x,y)-f_2(z,w)}{x-z} \\[8pt] \dfrac {f_1(z,y)-f_1(x,w)}{y-w} & \dfrac {f_2(z,y)-f_2(x,w)}{y-w} \end{matrix}\, \right |\in \mathbb {Z}[\mu, \,x,\,y,\,z,\,w]. \end{align*}

For any $F\in \mathbb {Q}[\mu ][x,y]$ , we define

(5.25) \begin{equation} \mathrm {Hess}\,F=\Bigg |\, \begin{matrix} \frac {\partial ^2}{\partial x^2}F & \frac {\partial ^2}{\partial x\partial y}F \\[4pt] \frac {\partial ^2}{\partial y\partial x}F & \frac {\partial ^2}{\partial y^2}F \end{matrix}\, \Bigg |. \end{equation}

Lemma 5.26. (Buchstaber-Leykin [8], p.64) Let $I$ be the ideal in $\mathbb {Q}[{\mu }][x,y,z,w]$ generated by $f_1(x,y)$ , $f_2(x,y)$ , $f_1(z,w)$ , and $f_2(z,w)$ . The determinant $\mathrm {ph}\big ((z,w),(x,y)\big )$ has the following properties. (1) $\mathrm {ph}\big ((x,y),(x,y)\big )=\mathrm {Hess}\,f(x,y)$ . (2) $\mathrm {ph}\big ((x,y),(z,w)\big )=\mathrm {ph}\big ((z,w),(x,y)\big )$ . (3) We have

\begin{align*} \mathrm {ph}\big ((z,w),(x,y)\big )\,F\big ((x,y),(z,w)\big ) \equiv \mathrm {ph}\big ((x,y),(z,w)\big )\,F\big ((z,w),(x,y)\big )\,\bmod {I} \end{align*}

for any $F\big ((x,y),(z,w)\big )\in \mathbb {Q}[{\mu }][x,y,z,w]$ .

Proof. (1) Taking the limit $z\to x$ after subtracting the second row times $\frac {y-w}{x-z}$ from the first row in $\mathrm {ph}\big ((z,w),(x,y)\big )\,F\big ((x,y),(z,w)\big )$ , we have

\begin{align*} \frac 12 \left | \begin{array}{c@{\quad}c} f_{11}(x,y)+f_{11}(x,w) & f_{21}(x,y)+f_{21}(x,w) \\[3pt] \dfrac {f_1(x,y)-f_1(x,w)}{y-w} & \dfrac {f_2(x,y)-f_2(x,w)}{y-w} \end{array} \right |, \end{align*}

where $f_{11}(x,y)=\frac {\partial ^2}{\partial x^2}(x,y)$ , etc. Then, by taking limit $y\to w$ we get $\mathrm {Hess}\,f(x,y)$ . (2) is trivial. (3) By expanding the matrix, we see that the numerator

(5.27) \begin{equation} \begin{aligned} &\ \ \ \ \big ( f_1(x,y)f_2(z,y) -f_1(x,y)f_2(x,w) -f_1(z,w)f_2(z,y) +f_1(z,w)f_2(x,w) \big )\\[3pt] &\hskip 5pt -\big ( f_1(z,y)f_2(x,y) -f_1(z,y)f_2(z,w) -f_1(x,w)f_2(x,y) +f_1(x,w)f_2(z,w) \big )\\[3pt] &=\big (f_1(x,y)f_2(z,y)-f_1(z,y)f_2(x,y)\big ) -\big (f_1(x,y)f_2(x,w)-f_1(z,y)f_2(z,w)\big )\\[3pt] &\hskip 5pt -\big (f_1(z,w)f_2(z,y)-f_1(x,w)f_2(x,y)\big ) +\big (f_1(z,w)f_2(x,w)-f_1(x,w)f_2(z,w)\big )\\[3pt] &=\big (f_1(x,y)f_2(z,y)-f_1(x,w)f_2(z,w)\big ) -\big (f_1(x,y)f_2(x,w)-f_1(x,w)f_2(x,y)\big )\\[3pt] &\hskip 5pt -\big (f_1(z,w)f_2(z,y)-f_1(z,y)f_2(z,w)\big ) +\big (f_1(z,w)f_2(x,w)-f_1(z,y)f_2(x,y)\big ) \end{aligned} \end{equation}

is divisible by $(z-x)(w-y)$ , because the second expression is clearly divisible by $(z-x)$ , while the third expression is divisible by $(w-y)$ . Hence, $\mathrm {ph}\big ((x,y),(x,y)\big )\in \mathbb {Q}[\mu ][x,y]$ . Moreover, the second expansion is equal to

\begin{align*} &\big (f_1(x,y)f_2(z,y)-f_1(x,y)f_2(x,y)+f_1(x,y)f_2(x,y)-f_1(z,y)f_2(x,y)\big )\\[3pt] -\,&\big (f_1(x,y)f_2(x,w)-f_1(x,y)f_2(z,w)+f_1(x,y)f_2(z,w)-f_1(z,y)f_2(z,w)\big )\\[3pt] -\,&\big (f_1(z,w)f_2(z,y)-f_1(z,w)f_2(x,y)+f_1(z,w)f_2(x,y)-f_1(x,w)f_2(x,y)\big )\\[3pt] +\,&\big (f_1(z,w)f_2(x,w)-f_1(z,w)f_2(z,w)+f_1(z,w)f_2(z,w)-f_1(x,w)f_2(z,w)\big )\\[3pt] =\,&f_1(x,y)\big (f_2(z,y)-f_2(x,y)\big )+\big (f_1(x,y)-f_1(z,y)\big )f_2(x,y)\\[3pt] -\,&f_1(x,y)\big (f_2(x,w)-f_2(z,w)\big )-\big (f_1(x,y)-f_1(z,y)\big )f_2(z,w)\\[3pt] -\,&f_1(z,w)\big (f_2(z,y)-f_2(x,y)\big )-\big (f_1(z,w)-f_1(x,w)\big )f_2(x,y)\\[3pt] +\,&f_1(z,w)\big (f_2(x,w)-f_2(z,w)\big )+\big (f_1(z,w)-f_1(x,w)\big )f_2(z,w), \end{align*}

which implies that $\mathrm {ph}\big ((x,y),(z,w)\big )(w-y)$ already belongs to $I$ . A similar calculation shows that $\mathrm {ph}\big ((x,y),(z,w)\big )(z-x)\in {I}$ . For $F\big ((z,w),(x,y)\big )=x^ay^b$ , by using (2), we see

\begin{align*} \begin{aligned} \mathrm {ph}&\big ((z,w),(x,y)\big )\,x^ay^b -\mathrm {ph}\big ((x,y),(z,w)\big )\,z^aw^b\\[3pt] & =\mathrm {ph}\big ((z,w),(x,y)\big )\,(x^ay^b-z^aw^b)\\[3pt] & =\mathrm {ph}\big ((z,w),(x,y)\big )\,(x^ay^b-x^aw^b+x^aw^b-z^aw^b)\\[3pt] & =\mathrm {ph}\big ((z,w),(x,y)\big )\,\big (x^a(y^b-w^b)+(x^a-z^a)w^b\big ) \in I. \end{aligned} \end{align*}

Hence, (3) has been proved.

Below, we will use, instead of $T$ , the symmetric $2g\times 2g$ matrix

\begin{align*} V=\underset {\substack {a\in \mathrm {wt}(M)\\[3pt]b\in \mathrm {wt}(\mu )}}{[\,V_{a,b}\,]} =\underset {\substack {1\leq i\leq 2g\\[3pt]1\leq j\leq 2g}} {[\,V_{v_i,\,eq-v_{\kern 0.5pt 2g-j+1}}\,]} \in \mathrm {Sym}(2g,\,\mathbb {Q}[\mu ]) \end{align*}

where all the indices run in increasing order, defined by the equation

(5.28) \begin{equation} {}^{t}{({}^{\mathrm {rev}}{M}}(x,y))\,\cdot {V}\cdot \,{}^{\mathrm {rev}}{M}(z,w)=f(x,y)\, \mathrm {ph}\big ((z,w),(x,y)\big )\,F\big ((x,y),(z,w)\big ) \end{equation}

in the ring

\begin{align*} \mathbb {Q}[\mu ][x,y,z,w]\,\big /\,I. \end{align*}

We note that the weight of any entry of $V$ is given by

(5.29) \begin{equation} \mathrm {wt}(V_{a,\,b})=-(a+b). \end{equation}

We define

\begin{align*} H=\underset {\substack {a\in \mathrm {wt}(M)\\[3pt]b\in \mathrm {wt}(\mu )}}{[\,H_{a-q+2,\,b-q-2}\,]} =\underset {\substack {1\leq i\leq 2g\\[3pt]1\leq j\leq 2g}}{[\,H_{v_i-q+2,\,eq-v_{\kern 0.5pt 2g-j+1}-q-2}\,]} \end{align*}

as the matrix given by

\begin{align*} \mathrm {ph}\big ((x,y),(z,w)\big )={}^{t}{({}^{\mathrm {rev}}{M}}(x,y))\,H\,{}^{\mathrm {rev}}{M}(z,w). \end{align*}

We see $H\in \mathrm {Mat}(2g,\,\mathbb {Q}[\mu ])$ by consideration of 5.27 in the proof of 5.25. Moreover, as for $V$ , the weight of any entry of $H$ is given by

\begin{align*} \mathrm {wt}(H_{a-q+2,\,b-q-2})=-(a+b-2q). \end{align*}

Example 5.30. In the case $(e,q)=(2,2g+1)$ , for $a=v_i=2i-2$ and $b=eq-v_{2g-j+1}=4g+2-2(2g-j+1)+2=2j+2$ with $1\leq i\leq g$ and $1\leq j\leq g$ , we see that

\begin{align*} \begin{aligned} \mathrm {wt}(V_{a,b})&=\mathrm {wt}(V_{2i-2,2j+2})=-2(i+j), \\[3pt] \mathrm {wt}(H_{a-q+2,\,b-q-2})& \,(\!=a+b-2q)=\mathrm {wt}(H_{v_i-(2g+1)+2,\,v_{2g-j+1}-(2g+1)-2}) =2(i-j)-(2g+1) \end{aligned} \end{align*}

Lemma 5.31. The matrix $H$ is of the form

(5.32)

If $e=2$ , then we have explicitly

(5.33)

Proof. Setting all the $\mu _j$ to be $0$ , we have

\begin{align*} \frac 12\,\left |\, \begin{matrix} \frac {q({-}x^{q-1}+z^{q-1})}{x-z} & \frac {e(y^{e-1}-w^{e-1})}{x-z} \\[10pt] \frac {q(x^{q-1}-z^{q-1})}{y-w} & \frac {e(y^{e-1}-w^{e-1})}{y-w} \end{matrix}\, \right | =-eq(x^{q-2}+x^{q-3}z+\cdots +z^{q-2})(y^{e-2}+y^{e-3}w+\cdots +w^{e-2}). \end{align*}

It follows that the counter-diagonal entries of $H$ are $-eq$ . From the definitions, the weight of $H$ is $-2(eq-e-q)$ and $\mathrm {wt}(M_{2g}(x,y))=-2g-1+w_g=-2(eq-q-e)$ . Therefore the entries below the counter-diagonal must be $0$ . For the case $e=2$ , we have

\begin{align*} \begin{aligned} \frac 12\,& \left |\ \begin{matrix} -\frac {q(x^{q-1}-z^{q-1})+(q-2)\mu _4(x^{q-3}-z^{q-3})+\cdots +\mu _{eq-e}(x-z)}{x-z} & \frac {2y-2w}{x-z} \\[3pt] \ \ \frac {q(x^{q-1}-z^{q-1})+(q-2)\mu _4(x^{q-3}-z^{q-3})+\cdots +\mu _{eq-e}(x-z)}{y-w} & \frac {2y-2w}{y-w} \end{matrix}\ \right |\\[3pt] &=-2\,\frac {q(x^{q-1}-z^{q-1})+(q-2)\mu _4(x^{q-3}-z^{q-3})+\cdots +\mu _{eq-e}(x-z)}{x-z}\\[3pt] &=-2\,\big (q(x^{q-2}+x^{q-3}z+\cdots +z^{q-2}) +(q-2)\mu _4(x^{q-4}+x^{q-5}z+\cdots +z^{q-4})+\cdots +\mu _{eq-e}\big ), \end{aligned} \end{align*}

giving the desired form of $H$ .

Lemma 5.34. We have $\det (V)=({-}1)^g\det (T)$ .

Proof. Since

\begin{align*} \begin{aligned} f(x,y)\,\mathrm {ph}\big ((x,y),(z,w)\big ) &=f(x,y)\,{}^{t}{({}^{\mathrm {rev}}{M}(z,w))}\,H\cdot \,{}^{\mathrm {rev}}{M}(x,y)\\[3pt] &\equiv {}^{t}{({}^{\mathrm {rev}}{M}}(z,w))\,{}^{\mathrm {rev}}{\!({-}\tfrac {1}{eq}\,T)}\,\,H\cdot \,{}^{\mathrm {rev}}{M}(x,y)\bmod {I} \end{aligned} \end{align*}

by (1.18), and the entries in $M(x,y)$ form a basis of $\mathbb {Q}[\mu ][x,y]/(f_1(x,y),f_2(x,y))$ , we see

(5.35) \begin{equation} V=-\tfrac 1{\,eq\,}\,{}^{\mathrm {rev}}{T}\,H. \ \ \end{equation}

Since $H$ is a skew-upper-triangular matrix of the form (5.32), we have proved $\det (V)=({-}1)^g\det (T)$ as desired.

Lemma 5.36. We have $\mathrm {wt}(\det V)=\mathrm {wt}(\det T)=-eq(e-1)(q-1)$ .

Proof. Since the determinants of $T$ and $V$ are of homogeneous weight, it suffices to check the sum of weights of the counter-diagonal entries, which is given by

\begin{align*} \sum _{q\in \mathrm {wt}(M)}\mathrm {wt}(T_{a,\,eq-a}) =\sum _{q\in \mathrm {wt}(M)}({-}eq)=-2geq=-eq(e-1)(q-1). \end{align*}

This is the same as $\mathrm {wt}(\det (V))$ and $\mathrm {wt}(\det (T))$ .

Lemma 5.37. We have $\mathrm {wt}(\varDelta )=-eq(e-1)(q-1)$ . If $\gcd (e-1,q-1)=1$ , then we have

\begin{align*} \det T=({-}1)^g\det V=c\cdot \varDelta \end{align*}

with $c\in \mathbb {Q}^{\times }$ .

Proof. Letting all the coefficients $\mu _j$ of $p_j(x)$ for $1\leq j\leq e-1$ to be zero, the discriminant $\varDelta$ becomes a power of the square of the difference of all the roots of $p_e(x)=0$ . Since the weight of any root is $-e$ , the weight of the square of the difference is

\begin{align*} 2\cdot \binom {q}{2}\cdot ({-}e)=-eq(q-1). \end{align*}

Similar arguments on $y$ shows that $\mathrm {wt}\,\varDelta$ is $-qe(e-1)$ times an positive integer. By the assumption $\gcd (e-1,q-1)=1$ , we have $\mathrm {wt}\,\varDelta$ is $-eq(e-1)(q-1)$ times a positive integer. The statement follows from 5.35 combined with 1.21 (1).

Remark 5.38. The condition $\gcd (e-1,q-1)=1$ in 5.36 holds if $e=2$ or $(e,q)=(3,4)$ , $(3,5)$ , for which we already know $\varDelta$ explicitly as mentioned in 1.9.

From now on we assume the modality of $C$ to be $0$ . For any $a\in \mathrm {wt}(M)$ , the coefficient $\mu _{eq-a}$ appears in the Weierstrass form, which is the reason why the modality is so important. Let

(5.39) \begin{equation} L_k = \sum _{j\in \mathrm {wt}(\mu )}\,V_{kj}\, \frac {\partial }{\partial \mu _j} \ \ \ (k\in \mathrm {wt}(M)). \end{equation}

It is natural to define

\begin{align*} \mathrm {wt}\left(\frac {\partial }{\partial \mu _{j}}\right)=j, \ \ \ \mathrm {wt}({L}_{v_i})=v_i. \end{align*}

We recall the definition of the matrix $\Gamma ^{L_k}$ for each $L_k$ ( $\mathrm {wt}(L_k)=-k$ ) (see 5.1), which we denote as ¹

\begin{align*} \Gamma ^{L_k} = \bigg [ \begin{array}{r@{\quad}c} -\beta _k &\ \ \alpha _k \\[3pt] -\gamma _k &\ {}^{t}{\!\beta _k} \end{array} \bigg ], \end{align*}

where $\alpha _k$ , $\gamma _k\in \mathrm {Sym}(g,\mathbb {Q}[\mu ])$ , and

(5.40) \begin{equation} \alpha _k=\underset {\substack {i\in \mathrm {wt}(u)\\[3pt] j\in \mathrm {wt}(u)}}{[\alpha _{k;\,-i,k-j}]}, \ \ \beta _k=\underset {\substack {i\in \mathrm {wt}(u)\\[3pt] j\in \mathrm {wt}(u)}}{[\beta _{k;\,j,k-i}]}, \ \ \gamma _k=\underset {\substack {i\in \mathrm {wt}(u)\\[3pt] j\in \mathrm {wt}(u)}}{[\gamma _{k;\,-i,k+j}]} \end{equation}

with decreasing order in $\mathrm {wt}(u)$ . Then the sum of two indices of any entry gives its weight;

\begin{align*} \mathrm {wt}(\alpha _{k;\,-i,k-j})=-i+(k-j), \ \ \mathrm {wt}( \beta _{k;\,j,k-i})=j+(k-i), \ \ \mathrm {wt}(\gamma _{k;\,-i,k+j})=-i+(k+j). \end{align*}

Note once again that $\Gamma ^{L_k}\in \mathrm {Mat}(2g,\mathbb {Q}[\mu ])$ follows from 2.1. Just to be sure, we shall redefine, as defined in (5.8),

(5.41) \begin{align} H^{L_k} &= \frac 1{\,2\,}\,\big [\,\tfrac {\partial \ }{\partial u_{w_g}} \ \cdots \ \tfrac {\partial \ } {\partial u_{w_1}} \ \ u_{w_g} \ \cdots \ u_{w_1}\,\big ] \Bigg [ \begin{array}{r@{\quad}c} \alpha _k &\ \,\beta _k \\[5pt] {}^{t}{\!\beta _k} &\ \,\gamma _k \end{array} \Bigg ]\! \left [ \begin{array}{c} \tfrac {\partial \ }{\partial u_{w_g}} \\[3pt] \vdots \\[3pt] \tfrac {\partial \ }{\partial u_{w_1}}\\[3pt] u_{w_g} \\[-2pt] \vdots \\[-4pt] u_{w_1} \end{array} \right ] \\[3pt] & =\frac 12\,\sum _{i\in \mathrm {wt}(u)}\sum _{j\in \mathrm {wt}(u)} \left({\alpha }_{k;\,-i,\,k-j}\,\frac {\partial ^2}{\partial \,u_i\partial \,u_j} \right. \nonumber \\[3pt] & \left.\ \ \ \ \ \ \ +2{\beta }_{k;\,j,k-i}\,u_i\,\frac {\partial \ \ }{\partial u_j} +{\gamma }_{k;-i,k+j}\ u_iu_j\right) +\tfrac 12\,{\mathrm {Tr}\,\beta _k}.\nonumber \end{align}

5.5. The operators tangent to the discriminant

We prove the following proposition for which there is no proof in [9].

Proposition 5.42. (Buchstaber-Leykin) Let

\begin{align*} L={M(x,y)}\,{}^{t}{[\,L_{v_1}\ L_{v_2}\ \cdots \ L_{v_{2g}}\,]}. \end{align*}

Then, in the ring $\mathbb {Q}[\mu ][x,y]/(f_1, f_2)$ , we have

(5.43) \begin{equation} L(\varDelta )=-\mathrm {Hess}f\cdot \varDelta . \end{equation}

Proof. For the case $e=2$ , $f(x,y)$ is of the form $y^2-p_2(x)$ . We denote $p_2(x)=p(x)$ for simplicity. Moreover, we denote $p^{\prime}(x)=\frac {\partial }{\partial x}p(x)$ and $p^{\prime\prime}(x)=\frac {\partial ^2}{\partial x^2}p(x)$ . In this case, the ring $\mathbb {Q}[\mu ][x,y]/(f_1,f_2)$ is identified with $\mathbb {Q}[\mu ][x]/(p^{\prime}(x))$ since $f_1(x,y)=\frac {\partial }{\partial y}f(x,y)=2y$ . Let $F$ be a splitting field of $p(x)$ . We write the factorisation of $p(x)$ in $F$ as $p(x) = (x-a_1)\cdots (x-a_q)$ . Then $\mu _{2i}$ is $({-}1)^i$ times the fundamental symmetric function of $a_1$ , $\cdots$ , $a_q$ of degree $i$ . Of course the ring $\mathbb {Q}[\mu ]$ is a sub-ring of $\mathbb {Q}[a_1,\,\cdots, \,a_q]$ . The Hessian of $f(x,y)=y^2-p(x)$ is

\begin{align*} \bigg |\, \begin{matrix} -p^{\prime\prime}(x) & 0 \\[3pt] 0 & 2 \end{matrix}\, \bigg | &=-2\,p^{\prime\prime}(x). \end{align*}

The main idea is to consider $\frac {\mathrm {Hess}\,f}{2f} = \frac {p^{\prime\prime}(x)}{p(x)}$ in the localised ring

\begin{align*} \big (F[x]/(p^{\prime}(x))\big )_{p(x)} \end{align*}

of $F[x]/(p^{\prime}(x))$ with respect to the multiplicative set $\{1,\,p(x),\,p(x)^2,\,\cdots \}$ (see [20], Section 4). The following calculation is done in the localised ring above. Since $\gcd (p^{\prime}(x),\,p(x))=1$ in this situation, we see $\big (F[x]/(p^{\prime}(x))\big )_{p(x)}=F[x]/(p^{\prime}(x))$ . Now, we have

\begin{align*} \frac {p^{\prime\prime}(x)}{p(x)} &=\sum _{(i,j),i\lt j}\frac {2}{(x-a_i)(x-a_j)} =\sum _{(i,j),i\lt j}\frac {2}{a_i-a_j}\left(\frac {1}{x-a_i} -\frac {1}{x-a_j}\right)\\[3pt] &=2\sum _{i=1}^q\left(\sum _{j\neq i}\frac {1}{a_i-a_j}\right)\frac {1}{x-a_i} =-2\sum _{i=1}^q\left(\sum _{j\neq i}\frac {1}{a_i-a_j}\right)\frac {1}{p^{\prime}(a_i)} \frac {-p^{\prime}(a_i)}{x-a_i}\\[3pt] &=-2\sum _{i=1}^q\left(\sum _{j\neq i}\frac {1}{a_i-a_j}\right)\frac {1}{p^{\prime}(a_i)} \frac {p^{\prime}(x)-p^{\prime}(a_i)}{x-a_i} = -2 \sum _{i=1}^q c_i\,\frac {p^{\prime}(x)-p^{\prime}(a_i)}{x-a_i}, \end{align*}

where

\begin{align*} c_i =\left(\sum _{j \neq i}\frac {1}{a_i-a_j}\right)\frac {1}{p^{\prime}(a_i)}. \end{align*}

Since $\mathrm {Hess}f(x,y)=-2p^{\prime\prime}(x)$ and $p(x)=-f(x,y)$ in the localised ring, it suffices to show that

\begin{align*} \frac {\partial }{\partial \mu _{2i}}\log \varDelta =-2\sum _{j=1}^q c_j {a_j}^{q-i} \end{align*}

up to a non-zero constant multiple. Indeed, if we have the formula above, we have

\begin{align*} \begin{aligned} \frac {L(x)\varDelta }{\varDelta } &=\sum _{i,k}M_i(x,y)V_{ik}\frac {\partial }{\partial \mu _{2i}}\log \varDelta =-2\sum _{i,k}M_i(x,y)V_{ik}\sum _{j=1}^qc_j{a_j}^{q-k}\\[3pt] &=-2\sum _{j=1}^qc_j\sum _{i,k}M_i(x,y)V_{ik}{a_j}^{q-k} =-2\sum _{j=1}^qc_j\,f(x,y)\,\mathrm {ph}\big ((x,y),(a_j,0)\big )\\[3pt] &=-2f(x,y)\,\sum _{j=1}^qc_j\,({-}2)\,\frac {p^{\prime}(x)-p^{\prime}(a_j)}{x-a_j} =-2f(x,y)\,\frac {p^{\prime\prime}(x)}{p(x)} =2p^{\prime\prime}(x) =-\mathrm {Hess}\,f(x,y). \end{aligned} \end{align*}

Here we have used

\begin{align*} \mathrm {ph}\big ((x,y),(a_j,0)\big ) =\frac 1{\,2\,} \left | \begin{array}{c@{\quad}c} \frac {-p^{\prime}(x)-p^{\prime}(a_j)\,}{x-a_j} & \frac {2y}{\,x-a_j\,}\\[3pt] \frac {-p^{\prime}(x)-p^{\prime}(a_j)\,}{y} & \frac {2y}{\,y\,} \end{array} \right | =-2\frac {\,p^{\prime}(x)-p^{\prime}(a_j)\,}{x-a_j}. \end{align*}

To calculate $\frac {\partial \log (\varDelta )}{\partial \mu _{2i}}$ , we remove the assumption $\mu _2=0$ . Since $\varDelta$ is some non-zero constant multiple of

\begin{align*} \prod _{i\lt j}(a_i-a_j)^2, \end{align*}

we easily get the $q\times q$ -matrix $\big [\frac {\partial \mu _{2i}}{\partial a_j}\big ]$ , and then we get $\frac {\partial \log (\varDelta )}{\partial \mu _{2i}}$ by using its inverse matrix. For $(e,q)=(3,4)$ , $(3,5)$ , we know only a proof by direct calculation with Maple by using the explicit form of $\varDelta$ and the operators $L_{v_j}$ s.

Remark 5.44. There is another proof of 5.41 in [28]).

The following lemma is required by the proof of the next proposition.

Lemma 5.45. The derivations $\ell _j$ s and $L_j$ s are liftable to the vector fields on $\mathscr {C}$ . Namely, there exist vector fields $\widetilde {\ell _j}$ s and $\widetilde {\ell _j}$ s on $\mathscr {C}$ such that their induced vector fields with respect to $\pi \,:\,\mathscr {C}\rightarrow \mathrm {Spec}\,\mathbb {Q}[\mu ]$ coincide with $\ell _j$ s and $L_j$ s, respectively.

Proof. Recall the definition of $T$ that is (2.5), namely,

\begin{align*} -eq\cdot f(X,Y)\cdot M_i=\sum _{b\in \mathrm {wt}{M}}^{2g}T_{a,b}\,M_a+A_a\,f_1(X,Y)+B_a\,f_2(X,Y). \end{align*}

Then the vector field

\begin{align*} \ell _i=\sum _{j=1}^{2g}T_{ij}\,\frac {\partial }{\,\partial \mu _{w_j}}\in \mathrm {Der}(\mathbb {Q}[\mu ]) \end{align*}

is liftable with respect to $\pi$ : $\mathscr {C}\rightarrow \mathrm {Spec}\,\mathbb {Q}[\mu ]$ . Indeed, if we define

\begin{align*} \widetilde {\ell }_i =\sum _{j=1}^{2g}T_{ij}\,\frac {\partial }{\,\partial \mu _{w_j}} +A_i\,\frac {\partial }{\,\partial x} +B_i\,\frac {\partial }{\,\partial y}, \end{align*}

namely, for any $G(\mu, X,Y)\in \mathbb {Q}[\mu, X,Y]$ ,

\begin{align*} \widetilde {\ell }_i\,:\, G(\mu, X,Y) \ \longmapsto \ \bigg (\,\sum _{j=1}^{2g}T_{ij}\,\frac {\partial }{\,\partial \mu _{w_j}} +A_i\,\frac {\partial }{\,\partial X} +B_i\,\frac {\partial }{\,\partial Y}\bigg )G(\mu, X,Y)\bigg |_{(X,Y)=(x,y)}, \end{align*}

we see at $(x,y,\mu )\in \mathscr {C}$ that

\begin{align*} \widetilde {\ell }_if =\sum _{j=1}^{2g}T_{ij}\,\frac {\partial f}{\,\partial \mu _{w_j}} +A_i\,\frac {\partial f}{\,\partial x} +B_i\,\frac {\partial f}{\,\partial y} =\sum _{j=1}^{2g}T_{ij}\,M_j+A_i\,f_1(x,y)+B_i\,f_2(x,y) =f(x,y)\cdot M_i=0. \end{align*}

Therefore $\widetilde {\ell }_i$ is a vector field on $\mathscr {C}$ and its restriction to $\mathrm {Spec}\,\mathbb {Q}[\mu ]$ is $\ell _i$ . We see similarly that $L_i$ is also liftable to $\mathscr {C}$ .

On the operators in $\boldsymbol {L}$ and the discriminant $\varDelta$ , we have the following.

Proposition 5.46. For a derivation $D\in \mathrm {Der}(\mathbb {Q}[{\mu }])$ , $D$ is tangent to the discriminant $\varDelta$ if and only if $D\in \boldsymbol {L}$ .

Proof. This follows from Kyoji Saito’s theorem (see Theorem A4 in [5]). See also Corollary 3 on p.2716 to the theorem on the previous page in [32] and Corollary 3.4 in [1]. However, the ‘ if ’-part of the statement for the cases $(e,q)=(2,q)$ , $(3,4)$ is contained in 5.41.

Obviously, we see

\begin{align*} \bigg [\bigoplus _i\mathbb {Q}[\mu ]\frac {\partial }{\,\partial \mu _i\,},\ \bigoplus _i\mathbb {Q}[\mu ]\frac {\partial }{\,\partial \mu _i\,}\bigg ] \subset \,\bigoplus _i\mathbb {Q}[\mu ]\frac {\partial }{\,\partial \mu _i\,}, \end{align*}

but on $\{\ell _i\}$ , we have the following.

Corollary 5.47. We have $[\ell _i,\,\ell _j]\in \bigoplus _i\mathbb {Q}[\mu ]\,\ell _i$ in $\mathrm {Der}(\mathbb {Q}[\mu ])$ . Moreover,

\begin{align*} \boldsymbol {L}=\bigoplus _i\mathbb {Q}[\mu ]\,\ell _i \subset \mathrm {Der}_{\mathbb {Q}[\mu ]}\left ( \mathbb {Q}[\mu, \,x,\,y]\frac {dx}{\,f_y\,} +d\,\bigg (\mathbb {Q}[\,\mu, \,x,\,y]\frac {1}{\,f_y\,}\bigg ) \right ). \end{align*}

Proof. Since $[\ell _i,\,\ell _j]$ is tangent to $\varDelta$ by 5.41, 5.45 shows the first assertion. Therefore, we have the second assertion from 2.2.

Because of 5.35, 5.47, and $\det ([H_{ij}])=(eq)^{2g}\in \mathbb {Q}$ , we see the Lie algebra generated by $L_k$ s in (5.39) is no other than $\boldsymbol {L}$ , namely,

(5.48) \begin{equation} \boldsymbol {L}=\bigoplus _k\mathbb {Q}[\mu ]\,L_k. \end{equation}

The structure constants of the algebra $\boldsymbol {L}$ with respect to $\{L_{v_j}\}$ belong to $\mathbb {Q}[\mu ]$ , so it is a polynomial Lie algebra, as discussed in [6]. The corresponding fundamental relations of $\{L_{v_j}\}$ for $(e,q)=(2,3)$ , $(2,5)$ , $(2,7)$ and $(3,4)$ are available on request.

5.6. The sigma function as a solution of the heat equations

Before showing that the function (4.16) is exactly the sigma function $\sigma (u)$ (see Lemma 4.17 in [9]), we shall first describe some heuristic arguments supporting this result.

From the definition of $L_0$ and 5.29, we have

(5.49) \begin{equation} L_0=\sum _j(eq-v_j)\mu _{eq-v_j}\frac {\partial }{\partial \mu _{eq-v_j}}, \ \text {and} \ \ L_0\big (F({\mu })\big )=-\mathrm {wt}\big (F({\mu })\big )F({\mu }) \end{equation}

for any homogeneous form $F({\mu })\in \mathbb {Q}[{\mu }]$ . The operator $L_0$ is called Euler vector field.

Lemma 5.50. On $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[\mu ])$ , we have

\begin{align*} {L}_0\,{}^{t}{\boldsymbol {\omega }} = \left [ \begin{array}{c@{\quad}c@{\quad}c|c@{\quad}c@{\quad}c} -w_g & & \\[-5pt] & \ddots & \\[-5pt] & & -w_1 & & & \\[3pt] \hline & & & w_g & & \\[-5pt] & & & & \ddots & \\[-5pt] & & & & & w_1 \end{array} \right ]{}^{t}{\boldsymbol {\omega }} =\Gamma _0{}^{t}{\boldsymbol {\omega }}. \end{align*}

Proof. For a power series expansion at $\infty$ of any 1-form $\omega$ of homogeneous weight $w$

\begin{align*} \omega =\sum _j c_j\,t^{j+w}\,dt, \end{align*}

where $t$ is a local parameter at $\infty$ of weight $1$ , $c_j\in \mathbb {Q}[{\mu }]$ is of homogeneous weight $-j-1$ ,

\begin{align*} \begin{aligned} L_0\left(\sum _j c_j t^{j+w}dt\right)&+w\sum _j c_j t^{j+w}dt =\sum _j (j+1)c_j t^{j+w}dt+\sum _j wc_j t^{j+w}dt\\[3pt] &=\sum _j (j+w+1)c_j t^{j+w}dt =d\left(\sum _j c_j\,t^{j+w+1}\right). \end{aligned} \end{align*}

If $\omega$ is any one of $\omega _{w_i}$ , which is of the form $\dfrac {h(x,y)}{f_2(x,y)}\,dx$ with $h(x,y)\in \mathbb {Q}[{\mu }][x,y]$ , we see the last above is

(5.51) \begin{equation} d\bigg (\frac {h(x,y)}{f_2(x,y)}\cdot {t}\,\frac {dx}{dt}\bigg ). \end{equation}

Since we can choose $t$ as a quotient of monomials of $x$ and $y$ (see [27], Section 3), (5.51) is an exact form. So that

\begin{align*} L_0(\omega )=-\mathrm {wt}(\omega )\,\omega \ \ \textrm {in} \, H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }]). \\[2pt] \nonumber \end{align*}

As $\mathrm {wt}(\omega _i)=i$ and $\mathrm {wt}(\eta _{-i})=-i$ , the statement is now obvious.

The function $\sigma (u)$ , characterised in 4.1, is a power series of homogeneous weight, which must be written as ²

(5.52) \begin{equation} \begin{aligned} \sigma &(u)={u_1}^{(e^2-1)(q^2-1)/24}\\[3pt] &\cdot \hskip -10pt\sum _{\{n_{eq-v_j},\,\ell _{w_i}\}} \hskip -10pt {a(\ell _{w_2},\cdots, \ell _{w_g},n_{eq-v_1},\cdots, n_{eq-v_{2g}}) \hskip 0pt\prod _{j=1}^{2g}(\mu _{eq-v_j}{u_1}^{eq-v_j})^{n_{eq-v_j}} \prod _{i=2}^g{\bigg (\dfrac {u_{w_i}}{{u_1}^{w_i}}\bigg )^{\ell _{w_i}}},} \end{aligned} \end{equation}

where the $a(\ell _{w_2},\cdots, \ell _{w_g},n_{eq-v_1},\cdots, n_{eq-v_{2g}})$ ’s are absolute constants and the set of $3g-1$ variables $\{n_{eq-v_j},\,\ell _{w_i}\}$ runs through the non-negative integers such that

\begin{align*} \frac {(e^2-1)(q^2-1)}{24}-\sum _{i=2}^g\ell _{w_i}+\sum _{j=1}^{2g}n_{eq-v_j}\geq 0. \end{align*}

Here, we shall mention that in Lemma 4.17 of [8] and its proof here along the lines of our reconstruction of BL theory, that is if $\sigma (u)$ can be written as $\sigma (u)=\varDelta ^{-M}\tilde {\sigma }(u)$ with a numerical constant $M$ , then $M=\frac 18$ . Before doing so, we point out the following lemma.

Lemma 5.53. The constant

(5.54) \begin{equation} \big ({(2\pi )^g}/{(\mathrm {det}\,{\omega ^{\prime}})}\big )^{\frac 12}\det (V)^{-\frac 18} =\big ({(2\pi )^g}/{(\mathrm {det}\,{\omega ^{\prime}})}\big )^{\frac 12}\det (T)^{-\frac 18}, \end{equation}

is of weight ${(e^2-1)(q^2-1)}/{24}$ . Hence, if $(e,q)=(2,3)$ , $(2,5)$ , $(2,7)$ , or $(3,4)$ , (see 5.36) or if the conjecture 1.23 is true, $\big ({(2\pi )^g}/{(\mathrm {det}\,{\omega ^{\prime}})}\big )^{\frac 12}\varDelta ^{-\frac 18}$ is also of weight ${(e^2-1)(q^2-1)}/{24}$ .

Proof. We know the weight of $\det (V)^{\frac 18}$ is $-eq(e-1)(q-1)/8$ by 5.35. The weight of $\mathrm {det}(\omega ^{\prime})$ is $\sum _{j=1}^gw_j$ , which equals

\begin{align*} \sum _{j=1}^gw_j=\frac {eq(e-1)(q-1)}4-\frac {(e^2-1)(q^2-1)}{12} \end{align*}

by p.97 of [7]. Hence the weight of the constant (5.54) is $\frac {(e^2-1)(q^2-1)}{24}$ .

Remark 5.55. (1) Note that the weight of the constant above is exactly that of $\sigma (u)$ . (2) From ( 5.24 ) and ( 5.54 ), we see the series ( 5.52 ) and both of

\begin{align*} \det (V)^{-\frac {1}{\,8\,}}\tilde {\sigma }(u) \ \ \text {and} \ \ \varDelta ^{-\frac {1}{\,8\,}}\tilde {\sigma }(u) \end{align*}

are killed by

(5.56) \begin{equation} \begin{aligned} L_0-&H^{L_0}-\frac {1}{\,8\,}L_0\log \varDelta =L_0-H^{L_0}+\mathrm {wt}(\sigma (u))\\[3pt] &=\sum _{j=1}^g(eq-v_j)\mu _{eq-v_j}\frac {\partial }{\partial \mu _{eq-v_j}} -\sum _{j=1}^g w_j\,u_{w_j}\frac {\partial }{\partial u_{w_j}} +\dfrac {(e^2-1)(q^2-1)}{24}. \end{aligned} \end{equation}

In the rest of the paper, we use the notation

\begin{align*} H_{v_i}=H^{L_{v_i}}-\tfrac 18{L}_{v_i}\log {\varDelta }, \end{align*}

where $H^{L_{v_i}}$ is defined by (5.41). Then 5.21 and (5.24) imply the following.

Theorem 5.57. We have $({L}_{v_j}-H_{v_j})\,\hat {\sigma }(u)=0$ for $j=1$ , $\cdots$ , $2g$ .

The following theorem is one of the important consequences of the BL theory.

Theorem 5.58. The function $\sigma (u)$ is equal to $\hat {\sigma }(u)$ up to a non-zero absolute constant.

Proof. For $(e,q)=(2,3)$ , $(2,5)$ , $(2,7)$ , and $(3,4)$ , we will solve the system of equations

(5.59) \begin{equation} (L_{v_i}-H_{v_i})\,\varphi (u)=0 \ \ \ (\,i=1, \ \cdots, \ 2g\,) \end{equation}

for an unknown entire function $\varphi (u)$ , and show that the solution space of this system is of dimension $1$ , in Section 6. Any solution eventually satisfies the properties of $\sigma (u)$ in (4.1). Hence we have proved that $\sigma (u)$ is equal to $\hat {\sigma }(u)$ up to a non-zero absolute constant.

From now on, throughout this paper, we denote

\begin{align*} \Gamma _{v_j}=\Gamma ^{L_{v_j}}. \end{align*}

Especially, $\Gamma _0=\Gamma ^{L_0}=\Gamma ^{L_{v_1}}$ .

Remark 5.60. As noted above in 5.7, our notation differs from that of Buchstaber and Leykin; we denote the matrix $\Gamma _j$ in p.274 of [9] by $\Gamma ^{\mathrm {BL}}_j$ and we define the sub-matrices of $-J\Gamma ^{\mathrm {BL}}_j$ and $\Gamma _{v_j}J$ by

\begin{align*} -J\Gamma ^{\mathrm {BL}}_j =\Bigg [\, \begin{matrix} \alpha ^{\mathrm {BL}}_j & {}^{t}{(\beta ^{\mathrm {BL}}_j)} \\[5pt] \beta ^{\mathrm {BL}}_j & \gamma ^{\mathrm {BL}}_j \end{matrix}\, \Bigg ], \ \ \Gamma _{v_j}J =\Bigg [\, \begin{matrix} \alpha _{v_j} & \beta _{v_j} \\[5pt] {}^{t}{(\beta _{v_j})} & \gamma _{v_j} \end{matrix}\, \Bigg ] \end{align*}

by following the notation of [9] and the present paper. Then we have for any $j$ that

\begin{align*} \alpha ^{\mathrm {BL}}_j=\alpha _{v_j}, \ \ \beta ^{\mathrm {BL}}_j={}^{t}{(\beta _{v_j})}, \ \ \gamma ^{\mathrm {BL}}_j=\gamma _{v_j}, \ \ \Gamma ^{\mathrm {BL}}_j={}^{t}{(\Gamma _{v_j})}. \end{align*}

6. Solving the heat equations

6.1. The initial conditions

For the rest of the paper, we shall solve the system of equations (5.59) for the $(2,3)$ -, $(2,5)$ -, $(2,7)$ -, and $(3,4)$ -curves. We frequently switch from regarding the $\mu _j$ s as indeterminates to regarding them as elements in $\mathbb {C}$ . We suppose the following two initial conditions for any solution $\varphi (u)$ solving (5.59): IC1. $\varphi (u)\in \mathbb {Q}[{\mu }][[u_{w_g},\,\cdots, \,u_{w_1}]]$ , and IC2. $\varphi (u)$ is of homogeneous weight $\frac {1}{\,24\,}(e^2-1)(q^2-1)$ with respect to $u_i$ s and $\mu _j$ s.

Since the property (4) in 4.1 is stronger than these conditions, there may be a possibility to reduce the characterisation in 4.1 of the sigma function, in general.

It is not clear to the authors which part of [9] shows that the space of the solutions $\varphi (u)=\varphi ({\mu },u_{w_g},\cdots, u_{w_2},u_{w_1}) \in \mathbb {Q}[{\mu }][[u_{w_g},\cdots, u_{w_2},u_{w_1}]]$ of (5.59) is one dimensional. The main part of the present paper, that is from 6.3 to the end of the paper, is a partial answer to this question.

6.2. General results for the $(2,3)$ -curve

In this subsection, we discuss the hyperelliptic case, that is the case $e=2$ . Firstly, we give the explicit expression for the entries of the matrix $V$ of (5.28). The authors know that the issue in this subsection is described in p.566 in V.I.Arnol’d’s [1] and p.65 in [2]. Since they do not know any source which contains a proof, we shall give a detailed proof here.

Lemma 6.1. We have

\begin{align*} \begin{aligned} V_{2i-2,\,2j+2}&=-\frac {2i(q-j)}{q}\,\mu _{2i}\mu _{2j} +\sum _{m=1}^{m_0}2(j-i+2m)\,\mu _{2(i-m)}\,\mu _{2(j+m)}\\[3pt] &=-\frac {2i(q-j)}{q}\,\mu _{2i}\mu _{2j} +\sum _{\ell =\ell _0}^{i-1\ \mathrm {or}\ j}2(i+j-2\ell )\,\mu _{2\ell }\, \mu _{2(i+j-\ell )}, \end{aligned} \end{align*}

where $\mu _0=1$ , $\mu _2=0$ , $m_0=\mathrm {min}\{i,\,q-j\}$ , and $\ell _0=\mathrm {max}\{0,i+j-q\}$ .

Proof. First of all, assuming the first equality, we show the second equality. To change the first expression to the second with summation to $i-1$ , we use the substitution $\ell =i-m$ . It is obvious that the second equality with summation to $i-1$ is equal to one with summation to $j$ for $i=j$ , $j+1$ . For the case of $i\lt j$ , the difference of the two is expressed as

\begin{align*} \sum _{\ell =i}^{j}2(i+j-2\ell )\,\mu _{2\ell }\,\mu _{2(i+j-\ell )} =-\sum _{\ell ^{\prime}=i}^{j}2(i+j-2\ell ^{\prime})\,\mu _{2(i+j-\ell ^{\prime})}\,\mu _{2\ell ^{\prime}} \end{align*}

setting $\ell ^{\prime}=i+j-\ell$ , it is clear that this vanishes. We see the case $j\lt i$ in a similar way. The matrix $V=[V_{2i-2,\,2j+2}]$ is symmetric by definition. However, if the Lemma is proved, we see this directly, by subtracting the term for $\ell =j$ from the first term. Now, noting that in the hyperelliptic case, the $M_{2j-2}(X,Y)$ are independent of $Y$ , we define $M^{(2i-2)}=M^{(2i-2)}(X)\in \mathbb {Z}[\mu ][X]$ by using $[H_{2i-q,\,2j-q}]$ of (5.33):

\begin{align*} M^{(2i-2)}(X)=\sum _{j=1}^{q-1}H_{2i-q,\,2j-q}M_{2q-2-2j}(X,Y) =\sum _{m=0}^{i-1}2(q+1+m-i)\,\mu _{2(i-m-1)}\,X^m. \end{align*}

While we are treating $f(X,Y)=Y^2-p_2(X)$ , we denote $p_2(X)$ by $p(X)$ in this proof, for a less cumbersome notation.

Since $f_1=p^{\prime}(X)$ , $f_2=2Y$ , we see $\mathbb {Q}[\mu ][X,Y]/(f_1,f_2)$ is isomorphic to $\mathbb {Q}[\mu ][X]/(p^{\prime}(X))$ . So that, it suffices to know explicitly the residue $V^{(i)}=V^{(i)}(X)$ of degree less than $q-1$ of the division of $p(X)\,M^{(2i-2)}(X)$ by $p^{\prime}(X)$ for $1\leq i\leq q-1$ . The key to this proof is that we actually know the quotient $Q^{(2i)}=Q^{(2i)}(X)\in \mathbb {Q}[\mu ][X]$ , as well as $V^{(2q+2i-2)}=V^{(2q+2i-2)}(X)$ defined below, of this division! Namely, we will show that, if we define functions

\begin{align*} Q^{(2i)}(X)=\sum _{m=1}^{i}2\mu _{2(i-m)}\,X^m+\frac {2i}{q}\,\mu _{2i}, \end{align*}

then the expression

(6.2) \begin{equation} V^{(2q+2i-2)}(X)=p(X)\,M^{(2i-2)}(X)-p^{\prime}(x)\,Q^{(2i)}(X) \end{equation}

is of degree less than $q-1$ . Moreover, we can calculate all the terms of $V^{(2q+2i-2)}$ explicitly, which are no other than the $V_{2i-2,\,2j-2}$ ’s.

Let us start to calculate each term of $X^k$ of the right-hand side of (6.2) for any $k\geq 0$ . We divide the calculation into four cases. (i) The case $k\geq q$ . In this case, $M^{(2i-2)}$ has terms only up to $X^{i-1}$ ( $i-1\leq q-2\lt q\leq k$ ), and $p(X)$ has terms up to $X^{q}$ ( $q\leq k$ ). Therefore, we find that the coefficient $C_{2k}$ of $X^k$ in $M^{(2i-2)}(X)\,p(X)$ is given by

\begin{align*} \begin{aligned} &C_{2k} =\sum _{m=k-q}^{i-1}2(q+1-i+m)\,\mu _{2(i-1-m)}\,\mu _{2(q-k+m)}\\[3pt] &=\sum _{m^{\prime}=q-1-k}^{i}2(k-m^{\prime}+1)\,\mu _{2(q-1-k+m^{\prime})}\,\mu _{2(i-m^{\prime})}, \end{aligned} \end{align*}

where we have changed the summation index by $q-k+m=i-m^{\prime}$ . On the other hand, $Q^{(2i)}$ has terms up to $X^{i}$ ( $i\leq q-1\lt q\leq k$ ), and $p^{\prime}(X)$ has terms up to $X^{q-1}$ ( $q-1\lt k$ ), so we see

\begin{align*} \textrm {``\,Coeff. of} \,X^k\, \textrm {in} Q^{(i)}(X)\,p^{\prime}(X)\,^{\prime\prime} =\!\!\!\sum _{m=k-q+1}^{i}\!\!2\,\mu _{2(i-m)}\,\mu _{2(q-1-k+m)}(k-m+1). \end{align*}

So the right-hand side of (6.2) has no term in $X^k$ for $k\geq q$ . (ii) The case $k=q-1$ . Since $M^{(2i-2)}$ has terms only up to $X^{i-1}$ ( $i-1\leq q-2\lt q-1=k$ ), we see that

\begin{align*} &\textrm {``\,Coeff. of} \,X^k\, \textrm {in} M^{(2i-2)}(X)\,p(X)\,^{\prime\prime} =\sum _{m=0}^{i-1}2(q+1-i+m)\,\mu _{2(i-1-m)}\,\mu _{2(1+m)}\\[3pt] &=\sum _{m^{\prime}=0}^{i-1}2(q-m^{\prime})\,\mu _{2m^{\prime}}\,\mu _{2(i-m^{\prime})} =\sum _{m^{\prime}=1}^{i-1}2(q-m^{\prime})\,\mu _{2m^{\prime}}\,\mu _{2(i-m^{\prime})}+2q\,\mu _0\mu _{2i}, \end{align*}

where we have changed the index of summation by $m+1=i-m^{\prime}$ . In this case $Q^{(2i-2)}$ has terms up to $X^{i}$ ( $i\leq q-1=k$ ), and $p^{\prime}(X)$ has terms up to $X^{q-1}$ ( $q=k$ ), we have that the coefficient $C_{2k}$ of $X^k$ in $Q^{(2i)}(X)\,p^{\prime}(X)$ is given by

\begin{align*} \begin{aligned} C_{2k}&=\sum _{m=1}^i2\,\mu _{2(i-m)}\,\mu _{2m}(q-m)+\frac {2i}{q} \mu _{2i}\,\mu _0\,q\\[3pt] &=\sum _{m=1}^{i-1}2\,\mu _{2(i-m)}\,\mu _{2m}(q-m)+2(q-i)\,\mu _0\,\mu _{2i} +2i\,\mu _{2i}\,\mu _0. \end{aligned} \end{align*}

So the right-hand side of (6.2) has no term in $X^{q-1}$ . (iii) The case $i-1\lt k\lt q-1$ . Since $M^{(2i-2)}$ has terms only up to $X^{i-1}$ , we see that the coefficient $D_{2k}$ of $X^k$ in $M^{(2i-2)}(X)\,p(X)$ is given by

\begin{align*} \begin{aligned} D_{2k}&=\sum _{m=0}^{i-1}2(q+1+m-i)\,\mu _{2(i-m-1)}\,\mu _{2(q-k+m)}\\[3pt] &=\sum _{m=1}^i2(q+m-i)\,\mu _{2(i-m)}\,\mu _{2(q-1-k+m)} \end{aligned} \end{align*}

by rewriting $m$ as $m-1$ . On the other hand, the coefficient $C_{2k}$ of $X^k$ in $Q^{(2i)}(X)\,p^{\prime}(X)$ is

\begin{align*} C_{2k}=\frac {2i}{q}\mu _{2i}\,(k+1)\mu _{q-1-k}+\sum _{m=1}^{i}2\,\mu _{2(i-m)} \,(k-m-1)\mu _{2(q-1-k+m)}. \end{align*}

So the coefficient of $X^k$ in the right-hand side of (6.2) is

\begin{align*} \sum _{m=1}^{i}2(q-1-k+2m-i)\,\mu _{2(i-m)}\,\mu _{2(q-1-k+m)} +\frac {2i}{q}(k+1)\mu _{2i}\,\mu _{2(q-1-k)} \end{align*}

and $V_{2i-2,\,2j-2}$ , which is no other than the value of this at $k=q-1-j$ , is given by

\begin{align*} \sum _{m=1}^{i}2(j+2m-i)\,\mu _{2(i-m)}\,\mu _{2(j+m)} +\frac {2i}{q}(q-j)\mu _{2i}\,\mu _{2j} \end{align*}

as desired since $i\lt k+1=q-j$ .

(iv) The case $k\lt i-1$ . Since $M^{(2i-2)}$ has terms up to $X^{i-1}$ , of higher degree than $X^k$ , we see that the coefficient $D_{2k}$ of $X^k$ in $M^{(2i-2)}(X)\,p(X)$ is given by

\begin{align*} \begin{aligned} D_{2k}&=\sum _{m=0}^k2(q+1+m-i)\,\mu _{2(i-m-1)}\,\mu _{2(q-k+m)}\\[3pt] &=\sum _{m=1}^{k+1}2(q+m-i)\,\mu _{2(i-m)}\,\mu _{2(q-1-k+m)} \end{aligned} \end{align*}

on replacing the summation index $m$ by $m+1$ . Similarly, $Q^{(2i)}$ has terms up to $X^i$ exceeding $X^k$ again, and

\begin{align*} &\textrm {``Coeff. of} \,X^k\, \textrm {in} p^{\prime}(X)\,Q^{(2i)}(X)\,^{\prime\prime}\\[3pt] &=\frac {2i}{q}\mu _{2i}\,\mu _{q-1-k}+\sum _{m=1}^{k+1}2\,\mu _{2(i-m)} \,(k-m-1)\mu _{2(q-1-k+m)} \end{align*}

with an extra term for $m=k+1$ which is zero. So the coefficient of $X^k$ in the right-hand side of (6.2) is

\begin{align*} \sum _{m=1}^{k+1}2(q-1-k+2m-i)\,\mu _{2(i-m)}\,\mu _{2(q-1-k+m)} +\frac {2i}{q}(k+1)\mu _{2i}\,\mu _{2(q-1-k)} \end{align*}

and then $V_{ij}$ , which is no other than the value of this at $k=q-1-j$ , is given by

\begin{align*} V_{2i-2,\,2j-2}=\sum _{m=1}^{q-j}2(j+2m-i)\,\mu _{2(i-m)}\,\mu _{2(j+m)} +\frac {2i}{q}(q-j)\mu _{2i}\,\mu _{2j} \end{align*}

as desired since $q-j=k+1\leq i$ .

Secondly, we give the values $L_{v_j}(\log \varDelta )=\frac {\,L_{v_j}\varDelta \,}{\varDelta }$ for the case $(e,q)=(2,q)$ .

Lemma 6.3. If $e=2$ , then we have $L_{2j}(\varDelta )=-2(q-j)(q-1-j)\mu _{2j}\,\varDelta$ for $0\leq j\leq q-2$ .

Proof. Since the Hessian of $f(X,Y)=Y^2-p_2(X)$ is

\begin{align*} \bigg |\, \begin{matrix} -{p_2}^{\prime\prime}(X) & 0 \\[3pt] 0 & 2 \end{matrix}\, \bigg | &=-2\,{p_2}^{\prime\prime}(X)\\[3pt] &=-2\big (q(q-1)X^{q-2}+(q-2)(q-3)\mu _4X^{q-4}+\cdots +2\cdot 1\,\mu _{q-3}\big ), \end{align*}

this lemma follows from (5.43).

6.3. Heat equations for the $(2,3)$ -curve

In this section we recall Weierstrass’ result which gives a recursive relation for the coefficients of the power series expansion of his sigma function at the origin. We refer the reader to (12) and (13) in p. 314 of [14] also. Here we derive Weierstrass’ result by following the method of [9], namely, following the theory described in previous sections, but without using the general results 6.1 and 6.3, in order to demonstrate the ideas of the theory.

Weierstrass’ original method is explained in [31] and some explanation of it is available in [25]. It is easy to get $L_0$ and $L_2$ :

(6.4) \begin{equation} V=\Bigg [\ \begin{matrix} 4\mu _4 & 6\mu _6\\[3pt] 6\mu _6 & -\frac 43{\mu _4}^2 \end{matrix}\ \Bigg ], \ \ \textrm {and}\ \ \left \{\ \begin{aligned} L_0&=4{\mu _4}\frac {\partial }{\partial \mu _4}+6{\mu _6}\frac {\partial } {\partial \mu _6}\\[3pt] L_2&=6{\mu _6}\frac {\partial }{\partial \mu _4}-\frac 43{\mu _4}^2 \frac {\partial }{\partial \mu _6}. \end{aligned} \right . \end{equation}

In this case, we see $V=T$ since

\begin{align*} \mathrm {ph}\big ((x,y),(z,w)\big )=-6x-6z=[\,x\ \ 1\,] \bigg [\, \begin{matrix} & -6 \\[3pt] -6 & \end{matrix}\, \bigg ]\, \bigg [ \begin{matrix} z \\[3pt] 1 \end{matrix} \bigg ]. \end{align*}

Then $\varDelta =2^2\cdot 3\cdot \det (V)$ (see 1.6). The differential forms

\begin{align*} \omega _1=\frac {dx}{2y}, \ \ \eta _{-1}=\frac {xdx}{2y} \end{align*}

form a symplectic basis of $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[\mu ])$ . We have $\boldsymbol {\omega }=(\,\omega _1, \ \eta _{-1}\,)$ . Bearing in mind Lemma 2.4, we proceed by using $x^{-\frac 12}$ as the local parameter satisfying $\frac {\partial }{\partial \mu _j}x=0$ for $j=4$ , $6$ , and we compute the matrix $\Gamma$ as follows. Using $f(x,y)=0$ , we see $2y\frac {\partial }{\partial \mu _4}y=x$ and $2y\frac {\partial }{\partial \mu _6}y=1$ , so that

\begin{align*} \frac {\partial }{\partial \mu _4}y=\frac {x}{2y}, \ \ \ \frac {\partial }{\partial \mu _6}y=\frac {1}{2y}. \end{align*}

Therefore, we have

(6.5) \begin{equation} \frac {\partial }{\partial \mu _6}\omega _1=-\frac {1}{4y^3}dx, \ \ \ \frac {\partial }{\partial \mu _4}\omega _1 =\frac {\partial }{\partial \mu _6} \eta _{-1}=-\frac {x}{4y^3}dx, \ \ \ \frac {\partial }{\partial \mu _4}\eta _{-1}=-\frac {x^2}{4y^3}dx, \end{equation}

and

(6.6) \begin{align} d\left(\frac {1}{y}\right) &=-\frac 1{y^2}dy =-\frac 1{y^2}\frac {dy}{dx}dx =-\frac 1{y^2}\,\frac {3x^2+\mu _4}{2y}\,dx =6\frac {\partial }{\partial \mu _4}\,\eta _{-1}+2\mu _4\frac {\partial } {\partial \mu _6}\,\omega _1,\notag \\[3pt] d\left(\frac {x}{y}\right) &=\frac {ydx-xdy}{y^2} =\frac {y-x\frac {dy}{dx}}{y^2}\,dx =\frac {y-x\frac {3x^2+\mu _4}{2y}}{y^2}\,dx\notag \\[3pt] &=\frac {y-\frac {3y^2-2\mu _4x-3\mu _6}{2y}}{y^2}\,dx =-\omega _1-4\mu _4\frac {\partial }{\partial \mu _4}\omega _1 -6\mu _6\frac {\partial }{\partial \mu _6}\omega _1 =-\omega _1-L_0\omega _1, \end{align}

(6.7) \begin{align} d\left(\frac {x^2}{y}\right) &=\frac {2xydx-x^2dy}{y^2} =\frac {2xy-x^2\frac {dy}{dx}}{y^2}\,dx =\frac {2xy-x^2\frac {3x^2+\mu _4}{2y}}{y^2}\,dx \\[3pt] &=\frac {2xy-\frac {3x(y^2-\mu _4x-\mu _6)+\mu _4\,x^2}{2y}}{y^2}\,dx =\frac {xdx}{2y}+\frac {\mu _4x^2}{y^3}dx+\frac {3}{2}\frac {\mu _6x}{y^3}dx \notag \\[3pt] &=\eta _{-1}-L_0\eta _{-1} \notag \\[3pt] &=\eta _{-1}+\frac 43{\mu _4}^2\frac {\partial }{\partial \mu _6}\omega _1 -6\mu _6\frac {\partial }{\partial \mu _4}\omega _1-\frac 23\mu _4d\left(\frac {1}{y}\right) \ \ \ \ \textrm {(\ by (6.6)\ )} \notag \\[3pt] &= \eta _{-1}-L_2\omega _1-\frac 23\mu _4d\left(\frac {1}{y}\right). \notag \end{align}

Accordingly, we see

\begin{align*} L_2\eta _{-1} &=6\mu _6\frac {\partial }{\partial \mu _4}\eta _{-1} -\frac 43{\mu _4}^2\frac {\partial }{\partial \mu _6}\eta _{-1}\\[3pt] &=-2\mu _6\mu _4\frac {\partial }{\partial \mu _6}\omega _1 -\frac 43{\mu _4}^2\frac {\partial }{\partial \mu _4}\omega _1 +\mu _6\,d\left(\frac 1{y}\right)\ \ \ \ \ \textrm {(\ by (6.5) and (6.6)\ )}\\[3pt] &=-\frac {\mu _4}{3}\left(6\mu _6\frac {\partial }{\partial \mu _6}\omega _1 +4\mu _4\frac {\partial }{\partial \mu _4}\omega _1\right) +\mu _6\,d\left(\frac 1{y}\right)\\[3pt] &=-\frac {\mu _4}{3}L_0\omega _1+\mu _6\,d\left(\frac 1{y}\right) =\frac {\mu _4}{3}\omega _1+\mu _6\,d\,\left(\frac 1{y}\right). \end{align*}

Summarising these results, we have on $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[\mu ])$ that

\begin{align*} L_0{}^{t}{\boldsymbol {\omega }}=\Gamma _0{}^{t}{\boldsymbol {\omega }}, \ \ L_2{}^{t}{\boldsymbol {\omega }}=\Gamma _2{}^{t}{\boldsymbol {\omega }}, \ \ \textrm {where}\ \ \Gamma _0 =\bigg [\, \begin{matrix} -1 & \\[3pt] & 1 \end{matrix}\, \bigg ], \ \ \Gamma _2 =\bigg [\, \begin{matrix} & 1 \\[3pt] \frac {\mu _4}3 & \end{matrix} \,\bigg ]. \end{align*}

Note that, by these equations, we have $L_j\varOmega =\Gamma _j\varOmega$ with $\varOmega =\bigg [\begin{matrix}\omega ^{\prime} & \omega ^{\prime\prime}\\[3pt]\eta ^{\prime} & \eta ^{\prime\prime} \end{matrix}\bigg ]$ as in (5.12). Since $(L_0,\,L_2)(\det (T))=(12,\,0)\det (T)$ (by 6.3), $\varDelta =2^2\cdot 3\cdot \det (T)$ , and (5.49), we have arrived at

(6.8) \begin{equation} \begin{aligned} (L_0-H_0)\sigma (u) &=\left (4{\mu _4}\frac {\partial }{\partial \mu _4} +6{\mu _6}\frac {\partial }{\partial \mu _6} -u\frac {\partial }{\partial u}+1\,\right )\varphi (u)=0,\\[3pt] (L_2-H_2)\sigma (u) &=\left (6{\mu _6}\frac {\partial }{\partial \mu _4} -\frac 43{\mu _4}^2\frac {\partial }{\partial \mu _6} -\frac 12\frac {\partial ^2}{\partial u^2} +\frac 16{\mu _4}u^2\,\right )\varphi (u)=0, \end{aligned} \end{equation}

where $H_j=H^{L_j}+\tfrac 18L_j\log \varDelta$ for $j=0$ and $2$ . From the first of (6.8) and the conditions IC1, IC2, the solution function is of the form

\begin{align*} \varphi (u)=u\sum _{n_4,n_6\geqq 0}b(n_4,n_6) \frac {(\mu _4u^4)^{n_4}(\mu _6u^6)^{n_6}}{(1+4n_4+6n_6)!}. \end{align*}

Using the second equation we then have a recurrence relation

(6.9) \begin{equation} \begin{aligned} b(&n_4,n_6)=\tfrac 23(4n_4+6n_6-1) (2n_4+3n_6-1)b(n_4-1,n_6)\\[3pt] &\qquad -\tfrac {8}{3}(n_6+1)b(n_4-2,n_6+1) +12(n_4+1)b(n_4+1,n_6-1) \end{aligned} \end{equation}

if $n_4\ge0,\ n_6\ge 0,\ (n_4,n_6) \ne (0,0)$ , and $b(n_4,n_6)=0$ if $n_4\lt 0$ or $n_6\lt 0$ . Since the term $b(n_4,n_6)$ on the left-hand side has weight $4n_4+6n_6$ , and the terms $b(i,j)$ on the right-hand side have weight smaller than this, all terms may be found from (6.9). Therefore, any solution of (6.8) is a constant times the function

\begin{align*} \varphi (u)=\sigma (u)=u +2\mu _4\tfrac {u^5}{5!} +24\mu _6\tfrac {u^7}{7!} -36\mu _4^2\tfrac {u^9}{9!} -288\mu _4\mu _6\tfrac {u^{11}}{11!} +\cdots . \end{align*}

6.4. Heat equations for the $(2,5)$ -curve

In this section, we list the analogous results for the heat equations for the curve

\begin{align*} \mathscr {C}_{{\mu }}\, :\, y^2=x^5+\mu _4x^3+\mu _6x^2+\mu _8x+\mu _{10}. \end{align*}

We note here that our results correct a sign in [8]; the overall constant $\frac 1{80}$ at the $4$ th line from bottom in page 68 of [8] should be $-\frac 1{80}$ . Here we give the Hurwitz series version of the algorithm. Now, we take a usual symplectic basis of differentials

\begin{align*} \omega _3=\frac {1}{2y}dx,\ \ \omega _1=\frac {x}{2y}dx,\ \ \eta _{-3}=\frac {3x^3+\mu _4x}{2y}dx,\ \ \eta _{-1}=\frac {x^2}{2y}dx \end{align*}

of $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[\mu ])$ . The matrix $V$ for this case is given by

\begin{align*} V= \left [\,\begin{matrix} 4\mu _{4} & 6\mu _{6} & 8\mu _{8} & 10\mu _{10} \\[3pt] 6\mu _{6} & -\tfrac {12}{5}\mu _{4}^2+8\mu _{8} & -\tfrac 85\mu _{4}\mu _{6}+10\mu _{10} & -\tfrac 45\mu _{4}\mu _{8} \\[3pt] 8\mu _{8} & -\tfrac 85\mu _{4}\mu _{6}+10\mu _{10} & -\tfrac {12}5\mu _{6}^2+4\mu _{4}\mu _{8} & 6\mu _{4}\mu _{10}-\tfrac 65\mu _{6}\mu _{8} \\[3pt] 10\mu _{10} & -\tfrac 45\mu _{4}\mu _{8} & 6\mu _{4}\mu _{10}-\tfrac 65\mu _{6}\mu _{8} & 4\mu _{10}\mu _{6}-\tfrac 85\mu _{8}^2 \end{matrix}\,\right ]. \end{align*}

A calculation by Maple along 1.5 gives $\varDelta =2^4\cdot 5\cdot \det (V)$ . The operators $L_j$ are given by

\begin{align*} {}^{t}{[L_0 \ L_2 \ L_4 \ L_6]} =V\, {}^{t}{\bigg [ \frac {\partial }{\partial \mu _4}\ \ \frac {\partial }{\partial \mu _6}\ \ \frac {\partial }{\partial \mu _8}\ \ \frac {\partial }{\partial \mu _{10}} \bigg ]}. \end{align*}

While the authors have the explicit commutation relations of these $L_i$ , we shall not include these here because their explicit forms are not needed in this paper. However, these commutators are all in the span of the $L_i$ . By 6.3, we see that these $L_j$ ’s operate on the discriminant $\varDelta$ as follows:

\begin{align*} [\,L_0\ \ L_2\ \ L_4\ \ L_6\,]\varDelta =[\,40\ \ \ 0\ \ 12\,\mu _4\ \ 4\,\mu _6\,]\varDelta . \end{align*}

The representation matrices $\Gamma _j$ for the $L_j$ acting on $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[\mu ])$ are

\begin{align*} \begin{aligned} \Gamma _0&= \left [\, \begin{matrix} -3 & & & \\[3pt] & -1 & & \\[3pt] & & 3 & \\[3pt] & & & 1 \end{matrix}\, \right ], \ \ \ \Gamma _2 =\left [\, \begin{matrix} & -1 & & \\[1pt] \tfrac 45\,\mu _4 & & & 1 \\[1pt] \tfrac 45\,{\mu _4}^{2}-3\mu _8 & & & -\tfrac 45\mu _4 \\[1pt] & \tfrac 35\,\mu _4 & 1 & \end{matrix}\, \right ],\\[3pt] \Gamma _4 &=\left [\, \begin{matrix} -\mu _4 & & & 1 \\[1pt] \tfrac 65\,\mu _6 & & 1 & \\[1pt] \tfrac 65\,\mu _4\mu _6-6\mu _{10} & -\mu _8 & \mu _4 & -\tfrac 65\mu _6 \\[1pt] -\mu _8 & \tfrac 25\,\mu _6 & & \end{matrix}\, \right ], \, \Gamma _6 =\left [\, \begin{matrix} & & 1 & \\[1pt] \tfrac 35\,\mu _8 & & & \\[1pt] \tfrac 35\,\mu _4\mu _8 & -2\,\mu _{10} & & -\tfrac 35\,\mu _8 \\[1pt] -2\,\mu _{10} & \tfrac 15\,\mu _8 & & \end{matrix}\, \right ]. \\[3pt] \end{aligned} \end{align*}

Therefore, we find the following operators $H_j$ :

\begin{align*} H_0&=3{u_3}\frac {\partial }{\partial {u_3}}+{u_1}\frac {\partial } {\partial {u_1}}-3,\\[3pt] H_2&=\frac 12\frac {\partial ^2}{\partial {u_1}^2} +{u_1}\frac {\partial }{\partial {u_3}} -\frac 45{\mu _4}{u_3}\frac {\partial }{\partial {u_1}} -\frac 3{10}{\mu _4}{u_1}^2 -\left(\frac 32{\mu _8}-\frac 25{\mu _4}^2\right){u_3}^2,\\[3pt] H_4&=\frac {\partial ^2}{\partial {u_1}\partial {u_3}} -\frac 65{\mu _6}{u_3}\frac {\partial }{\partial {u_1}} +{\mu _4}{u_3}\frac {\partial }{\partial {u_3}} -\frac 15{\mu _6}{u_1}^2+{\mu _8}{u_1}{u_3}+\left(3{\mu _{10}}-\frac 35{\mu _4}{\mu _6}\right){u_3}^2{-\,\mu _4,}\\[3pt] H_6&=\frac 12\frac {\partial ^2}{\partial {u_3}^2} -\frac 35{\mu _8}{u_3}\frac {\partial }{\partial {u_1}} -\frac 1{10}{\mu _8}{u_1}^2 +2{\mu _{10}}{u_3}{u_1} -\frac 3{10}{\mu _8}{\mu _4}{u_3}^2 -\frac 12{\mu _6}. \end{align*}

By the equation $(L_0-H_0)\,\varphi (u)=0$ and the conditions IC1 and IC2, the solution function must be of the form

\begin{align*} \varphi (u)=\sigma (u_3,u_1)&= \sum _{\substack {m,n_4,n_6,n_8,n_{10}\geq 0\\[3pt]3-3m+4n_4+6n_6+8n_8+10n_{10}\geq 0}} \hskip -20pt \Big [\,b(m,n_4,n_6,n_8,n_{10})\\[3pt] &\cdot \frac {{u_1}^3\left(\dfrac {u_3}{{u_1}^3}\right)^m \left(\mu _4{u_1}^4\right)^{n_4} \left(\mu _6{u_1}^6\right)^{n_6} \left(\mu _8{u_1}^8\right)^{n_8} \left(\mu _{10}{u_1}^{10}\right)^{n_{10}}} {m!\,(3-3m+4n_4+6n_6+8n_8+10n_{10})!}\ \Bigg ]. \end{align*}

Let $k=3-3m+4n_4+6n_6+8n_8+10n_{10}$ . Then the other heat equations $(L_j-H_j)\,\varphi (u)=0$ imply the following recursion scheme:

\begin{align*} b(m,n_4,n_6,n_8,n_{10}) =\left \{ \begin{aligned} \ B_2 & \ \ \ (\,\textrm {if} k\gt 1 and m\geq 0\,) \\[3pt] \ B_1 & \ \ \ (\,\textrm {if} k=1 and m\gt 0\,) \\[3pt] \ B_0 & \ \ \ (\,\textrm {if} k=0 and m\gt 1\,), \end{aligned} \right . \end{align*}

where the $B_i$ are given by

\begin{align*} B_2= 20(n_8+1)\,&b(m, n_4, n_6, n_8+1,n_{10}-1)\\[3pt] +16(n_6+1)\,&b(m, n_4, n_6+1,n_8-1,n_{10} )\\[3pt] +12(n_4+1)\,&b(m, n_4+1,n_6-1,n_8, n_{10} )\\[3pt] -\tfrac {24}5(n_6+1)\,&b(m, n_4-2,n_6+1,n_8, n_{10} )\\[3pt] +\tfrac 35(k-3)(k-2)\,&b(m, n_4-1,n_6, n_8, n_{10} )\\[3pt] -\tfrac 85(n_{10}+1)\,&b(m, n_4-1,n_6, n_8-1,n_{10}+1)\\[3pt] -\tfrac {16}5(n_8+1)\,&b(m, n_4-1,n_6-1,n_8+1,n_{10} )\\[3pt] -2(k-2)\,&b(m+1,n_4, n_6, n_8, n_{10} )\\[3pt] -3m(m-1)\,&b(m-2,n_4, n_6, n_8-1,n_{10} )\\[3pt] +\tfrac 45m(m-1)\,&b(m-2,n_4-2,n_6, n_8, n_{10} )\\[3pt] +\tfrac 85m\,&b(m-1,n_4-1,n_6, n_8, n_{10} ),\\[3pt] B_1= +10(n_6+1)\,&b(m-1,n_4, n_6+1,n_8, n_{10}-1)\\[3pt] -\tfrac {12}5(n_8+1)\,&b(m-1,n_4, n_6-2,n_8+1,n_{10} )\\[3pt] -\tfrac 65(n_{10}+1)\,&b(m-1,n_4, n_6-1,n_8-1,n_{10}+1)\\[3pt] +8(n_4+1)\,&b(m-1,n_4+1,n_6, n_8-1,n_{10} )\\[3pt] -\tfrac 15(5m{-}10{+}8n_6{-}20n_8{-}30n_{10})\,&b(m-1,n_4-1,n_6, n_8, n_{10} )\\[3pt] -3(m-1)(m-2)\,&b(m-3,n_4, n_6, n_8, n_{10}-1)\\[3pt] +\tfrac 35(m-1)(m-2)\,&b(m-3,n_4-1,n_6-1,n_8, n_{10} )\\[3pt] +\tfrac 65(m-1)\,&b(m-2,n_4, n_6-1,n_8, n_{10}), \\[3pt] B_0=\ \ -\tfrac {16}5(1+n_{10})\,&b(m-2,n_4, n_6, n_8-2,n_{10}+1)\\[3pt] -\tfrac 15(12n_8-40n_{10}-5)\,&b(m-2,n_4, n_6-1,n_8, n_{10} )\\[3pt] +20(n_4+1)\,&b(m-2,n_4+1,n_6, n_8, n_{10}-1)\\[3pt] +12(n_8+1)\,&b(m-2,n_4-1,n_6, n_8+1,n_{10}-1)\\[3pt] -\tfrac 85(n_6+1)\,&b(m-2,n_4-1,n_6+1,n_8-1,n_{10} )\\[3pt] +\tfrac 35(m-2)(m-3)\,&b(m-4,n_4-1,n_6, n_8-1,n_{10} )\\[3pt] +\tfrac 65(m-2)\,&b(m-3,n_4, n_6, n_8-1,n_{10}). \end{align*}

From these, we see that the expansion of $\sigma (u)$ is Hurwitz integral over $\mathbb {Z}[\tfrac 15]$ .

Remark 6.10. Actually, the above recurrence scheme is one of several possible recurrence relations. However, we see any such system gives the same solution space by the following argument. Here, of course, we suppose that $b(m, n_4, \cdots, n_{10})=0$ if $k$ or any of the explicit arguments is negative. For any finite subset $S\subset \{(m,\,n_4,\,\cdots, \,n_{10})\,|\,k,\,n_4,\,\cdots, \,n_{10}\geq 0\}$ , we take the set $E_S$ of relations $h$ between $\{b(m,\,n_4,\,\cdots, \,n_{10})\}$ such that any $b(m,\,n_4,\,\cdots, \,n_{10})$ appears as a term in $h$ provided that $(m,n_4,\cdots, n_{10})\in S$ . For instance, if we consider

\begin{align*} S= \{ (1,0,0,0,0),\ (0,0,0,0,0),\ (0,1,0,0,0),\ (1,1,0,0,0), \ (2,1,0,0,0)\}, \end{align*}

then $E_S$ consists of the following $4$ equations:

\begin{align*} \begin{aligned} b(0,0,0,0,0)& = -2b(1,0,0,0,0), \\[3pt] b(0,1,0,0,0)& = 12b(0,0,0,0,0)-10b(1,1,0,0,0),\\[3pt] b(1,1,0,0,0)& = \tfrac 65 b(1,0,0,0,0)-4b(2,1,0,0,0) -\tfrac {16}5b(0,0,0,0,0),\\[3pt] b(2,1,0,0,0)& = \tfrac 15\cdot {0}\cdot {}b(1,0,0,0,0). \end{aligned} \end{align*}

The solution space of such a system of linear equations $E_S$ is of dimension 1 or larger because we have at least one iteration system as above whose solution space is of dimension $1$ . Since $E_S$ is independent of the choice of recursion system, any recursion system must include the same solution space of dimension $1$ .

The first few terms of the sigma expansion are given as follows (up to a constant multiple):

\begin{align*} \begin{aligned} \sigma ({u_3}&,{u_1})={u_3}-2\frac {{u_1}^3}{3!} -4\mu _4\frac {{u_1}^7}{7!} -2\mu _4\frac {{u_3}{u_1}^4}{4!} +64\mu _6\frac {{u_1}^9}{9!} -8\mu _6\frac {{u_3}{u_1}^6}{6!}\\[3pt] &-2\mu _6\frac {{u_3}^2{u_1}^3}{2!3!} +\mu _6\frac {{u_3}^3}{3!} +(1600\mu _8-408{\mu _4}^2)\frac {{u_1}^{11}}{11!}\\[3pt] &-(4{\mu _4}^2+32\mu _8)\frac {{u_3}{u_1}^8}{8!} -8\mu _8\frac {{u_3}^2{u_1}^5}{2!5!} -2\mu _8\frac {{u_3}^3{u_1}^2}{3!2!} +\cdots . \end{aligned} \end{align*}

6.5. The heat equations for the $(2,7)$ -curve

We take the hyperelliptic genus three curve $\mathscr {C}$ in the Weierstrass form

\begin{align*} y^2=f(x)=x^7+\mu _4x^5+\mu _6x^4+\mu _8x^3+\mu _{10}x^2+\mu _{12}x+\mu _{14}. \end{align*}

The discriminant $\varDelta$ of $\mathscr {C}$ is the resultant of $f$ and $f_1$ . It has $320$ terms and is of weight $84$ . The matrix $V$ is given by

\begin{align*} V&=\left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 4\,\mu _4 & 6\,\mu _6 & 8\,\mu _8 \\[3pt] 6\,\mu _6 & -\tfrac 47\,\left (5\,{\mu _4}^2-14\,\mu _8 \right ) & -\tfrac 27\,\left (8\,\mu _6\mu _4 -35\,\mu _{10}\right ) \\[3pt] 8\,\mu _8 & -\tfrac 27\,\left (8\,\mu _6\mu _{{4}}-35\,\mu _{10}\right ) & \tfrac 47\,\left (21\,\mu _{12}-6\,{\mu _6}^{2}+7\,\mu _4\mu _8\right ) \\[3pt] 10\,\mu _{10} & -\frac {12}{7}\,\left (\mu _4\mu _8-7\,\mu _{12} \right ) & \tfrac 27\,\left (49\,\mu _{14}-9\,\mu _6\mu _8+21\,\mu _4\mu _{10}\right ) \\[3pt] 12\,\mu _{12} & -\tfrac 27\,\left (4\,\mu _4\mu _{10} -49\,\mu _{14}\right ) & \tfrac 47\,\left (14\,\mu _4\mu _{12}-3\,\mu _6\mu _{10}\right ) \\[3pt] 14\,\mu _{14} & -\tfrac 47\,\mu _4\mu _{12} & \tfrac 27\,\left (35\,\mu _4 \mu _{14} -3\,\mu _6\mu _{12} \right ) \end{array}\right . \end{align*}

\begin{align*} &\left . \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} & 10\,\mu _{10} & 12\,\mu _{12} \\[3pt] & -\tfrac {12}{7}\,\left (\mu _4\mu _8-7\,\mu _{12}\right ) & -\tfrac 27\,\left (4\,\mu _4\mu _{10}-49\,\mu _{14}\right ) \\[3pt] & \tfrac 27\,\left (21\,\mu _4\mu _{10}-9\,\mu _6\mu _8+49\,\mu _{14}\right ) & \tfrac 47\,\left (14\,\mu _4\mu _{12}-3\,\mu _6\mu _{10}\right ) \\[3pt] & \tfrac 47\,\left (7\,\mu _6\mu _{10} -6\,{\mu _8}^{2}+14\,\mu _4\mu _{12} \right ) & \tfrac 27\,\left (21\,\mu _6\mu _{12}-8\,\mu _{10}\mu _8+35\,\mu _4\mu _{14}\right ) \\[3pt] & \tfrac 27\,\left (21\,\mu _6\mu _{12} -8\,\mu _{10}\mu _8 +35\,\mu _4\mu _{14}\right ) & \tfrac 47\,\left (7\,\mu _{12}\mu _8- 5\,{\mu _{10}}^2+14\,\mu _6\mu _{14}\right ) \\[3pt] & \tfrac {8}{7}\,\left (7\,\mu _6\mu _{14} - \mu _{12}\mu _8\right ) & \tfrac 27\, \left (21\,\mu _{14}\mu _8 -5\,\mu _{12}\mu _{10}\right ) \end{array}\right .\\[3pt] &\hskip 100pt\left . \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} & 14\,\mu _{14} \\[3pt] & -\tfrac 47\,\mu _4\mu _{12} \\[3pt] & \tfrac 27\,\left (35\,\mu _4\mu _{14} -3\,\mu _6\mu _{12}\right ) \\[3pt] & \frac {8}{7}\,\left (7\,\mu _6\mu _{14} -\mu _{12}\mu _8 \right ) \\[3pt] & \tfrac 27\,\left (21\,\mu _{14}\mu _8 -5\,\mu _{12}\mu _{10}\right ) \\[3pt] & \tfrac 47\,\left (7 \,\mu _{14}\mu _{10} -3\,{\mu _{12}}^{2}\right ) \end{array}\right ]. \end{align*}

Here a calculation by Maple along 1.5 shows that $\varDelta =2^6\cdot 7\cdot \det (V)$ . Then we have

\begin{align*} {}^{t}{[L_0 \ L_2 \ L_4 \ L_6 \ L_8 \ L_{10}]}=V {}^{t}{\bigg [\frac {\partial }{\partial \mu _4}\ \ \frac {\partial }{\partial \mu _6}\ \ \frac {\partial }{\partial \mu _8}\ \ \frac {\partial }{\partial \mu _{10}}\ \ \frac {\partial }{\partial \mu _{12}}\ \ \frac {\partial }{\partial \mu _{14}}\bigg ]}. \end{align*}

Using 6.3, their operation on $\varDelta$ are given by

\begin{align*} [L_0 \ L_2 \ L_4 \ L_6 \ L_8 \ L_{10}](\varDelta )=[84 \ \ 0 \ \ 40\mu _4 \ \ 24\mu _6 \ \ 12\mu _8 \ \ 4\mu _{10}]\varDelta . \end{align*}

As for the $(2,5)$ -case, we have fundamental relations for these ${L}_i$ as a set of generators of certain Lie algebra, which we do not include here. The symplectic basis of $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }])$ is

\begin{align*} \begin{aligned} &\omega _5=\frac {dx}{2y}, \ \ \ \omega _3=\frac {xdx}{2y}, \ \ \ \omega _1=\frac {x^2dx}{2y}, \ \ \eta _{-5}=\frac {(5x^5+3\mu _4x^3+2\mu _6x^3+\mu _8x^2)dx}{2y}, \\[3pt] &\eta _{-3}=\frac {(3x^4+\mu _4x^2)dx}{2y}, \ \ \eta _{-1}=\frac {x^3dx}{2y}. \end{aligned} \end{align*}

With respect to these, the matrices $\Gamma _j ={\bigg [ \begin{array}{c@{\quad}c} -\beta _j & \alpha _j \\[3pt] -\gamma _j & {}^{t}{\beta _j}\end{array} \bigg ]}$ are given as follows:

\begin{align*} \alpha _0 & = O, \ \ \beta _0 = \left [ \begin{array}{c@{\quad}c@{\quad}c} 5 & & \\[-4pt] & 3 & \\[-4pt] & & 1 \end{array} \right ], \ \ \gamma _0=O,\\[3pt]\alpha _2 &=\left [ \begin{array}{c@{\quad}c@{\quad}c} & & \\[3pt] & & \\[3pt] \ \ & \ \ & 1 \end{array} \right ], \ \beta _2=\left [ \begin{array}{c@{\quad}c@{\quad}c} & 3 & \\[3pt] -\tfrac 47\mu _4 & & 1 \\[3pt] & -\tfrac 87\mu _4 & \end{array}\right ], \nonumber \\[3pt] & \qquad \gamma _2 =\left [ \begin{array}{c@{\quad}c@{\quad}c} -\tfrac 17(4\mu _4\mu _8-35\mu _{12}) & & \\[3pt] & -\tfrac 17(8{\mu _4}^2-21\mu _8) & \\[3pt] & & -\tfrac 57\mu _4 \end{array} \right ],\end{align*}

\begin{align*} \alpha _4 &=\left [\begin{array}{c@{\quad}c@{\quad}c} & & \\[3pt] & & 1 \\[3pt] \ \ & 1 & \end{array} \right ], \ \ \beta _4 =\left [ \begin{array}{c@{\quad}c@{\quad}c} 3\mu _4 & & 1 \\[3pt] -\tfrac 67\mu _6 & \mu _4 & \\[3pt] & -\frac {12}7\mu _6 & \end{array} \right ], \nonumber \\[3pt] & \qquad \gamma _4 =\left [ \begin{array}{c@{\quad}c@{\quad}c} -\tfrac 27(3\mu _6\mu _8-35\mu _{14}) & 3\mu _{12} & \\[3pt] 3\mu _{12} & -\tfrac 67(2\mu _4\mu _6-7\mu _{10}) & \mu _8 \\[3pt] & \mu _8 & -\tfrac 47\mu _6 \end{array} \right ], \\[3pt] \alpha _6 &=\left [ \begin{array}{c@{\quad}c@{\quad}c} & & 1 \\[3pt] & 1 & \\[3pt] 1 & & \end{array} \right ], \ \beta _6 =\left [ \begin{array}{c@{\quad}c@{\quad}c} 2\mu _6 & \mu _4 & \ \ \ \ \ \ \\[3pt] -\frac 87\,\mu _8 & & \\[3pt] & -\tfrac 97\mu _8 & \end{array} \right ], \nonumber\\ & \qquad \gamma _6 =\left [ \begin{array}{c@{\quad}c@{\quad}c} 3\mu _4\mu _{12}-\tfrac 87{\mu _8}^2 & 6\mu _{14} & \mu _{12} \\[3pt] 6\mu _{14} & -\tfrac 97\mu _4\mu _8+9\mu _{12} & 2\mu _{10} \\[3pt] \mu _{12} & 2\mu _{10} & -\tfrac 37\mu _8 \end{array} \right ], \\[3pt] \alpha _{8} &=\left [ \begin{array}{c@{\quad}c@{\quad}c} & 1 & \\[3pt] 1 & & \\[3pt] & & \end{array} \right ], \ \ \beta _8 =\left [ \begin{array}{c@{\quad}c@{\quad}c} \mu _8 & & \ \ \ \ \ \ \ \ \\[3pt] -\tfrac {10}7\mu _{10} & & \\[3pt] \mu _{12} & -\tfrac 67\mu _{10} & \end{array} \right ], \\[3pt] \qquad &\gamma _8 =\left [ \begin{array}{c@{\quad}c@{\quad}c} 6\mu _4\mu _{14}+2\mu _6\mu _{12}-\tfrac {10}7\mu _8\mu _{10} & \mu _4\mu _{12} & 2\mu _{14} \\[3pt] \mu _4\mu _{12} & -\tfrac 67\mu _4\mu _{10}+12\mu _{14} & 3\mu _{12} \\[3pt] 2\mu _{14} & 3\mu _{12} & -\tfrac 27\mu _{10} \end{array} \right ], \\[3pt] \alpha _{10} & = \left [ \begin{array}{c@{\quad}c@{\quad}c} 1 & \ \ \ & \ \ \ \\[3pt] & & \\[3pt] & & \end{array} \right ], \quad \beta _{10} = \left [ \begin{array}{c@{\quad}c@{\quad}c} \ \ \ \ \ \ & & \ \ \ \ \ \ \ \ \ \\[3pt] -\frac 57\,\mu _{12} & & \\[3pt] 2\,\mu _{14} & -\frac 37\,\mu _{12} & \end{array} \right ], \nonumber\\[3pt] & \qquad \gamma _{10} = \left [ \begin{array}{c@{\quad}c@{\quad}c} 4\,\mu _6\mu _{14}-\frac 57\,\mu _{8}\mu _{12} & 2\,\mu _4\mu _{14} & \\[3pt] 2\,\mu _4\mu _{14} & -\frac 37\,\mu _4\mu _{12} & 4\,\mu _{14} \\[3pt] & 4\,\mu _{14} & -\frac 17\,\mu _{12} \end{array} \right ]. \end{align*}

These give a set of heat equations $(L_j-H_j)\,\sigma (u)=0$ as before.

6.6. The sigma function for the $(2,7)$ -curve

We now solve (5.59) in the $(2,7)$ case. The initial conditions IC1, IC2 of (5.59) in this case are as follows:

\begin{align*} \varphi (u)\in \mathbb {Q}[{\mu }][[u_5,\,u_3,\,u_1]], \,\textrm {and} \,\varphi (u)\,\textrm {is of homogeneous weight} 6. \end{align*}

Following [8] but in the Hurwitz series form as [31], we write any solution $\varphi (u)$ as

\begin{align*} \begin{aligned} \varphi &(u_5,u_3,u_1)=\sum _{\substack {{\ell },m,n_4,n_6,n_8,\\[3pt] n_{10},n_{12},n_{14}}} \!\Bigg [\,b({\ell },m,n_4,n_6,n_8,n_{10},n_{12},n_{14})\,\\[3pt] &\cdot \left (\mu _4{u_1}^4\right )^{n_4} \left (\mu _6{u_1}^6\right )^{n_6} \left (\mu _8{u_1}^8\right )^{n_8} \left (\mu _{10}{u_1}^{10}\right )^{n_{10}} \left (\mu _{12}{u_1}^{12}\right )^{n_{12}} \left (\mu _{14}{u_1}^{14}\right )^{n_{14}}\\[3pt] &\cdot \frac {{u_1}^6 \left(\dfrac {u_5}{{u_1}^5}\right)^{\ell } \left(\dfrac {u_3}{{u_1}^3}\right)^m} {\,(6-5{{\ell }}-3m+4n_4+6n_6+8n_8+10n_{10}+12n_{12}+14n_{14})!\,{{\ell }}!\,m!\,}\Bigg ], \end{aligned} \end{align*}

giving a solution of $(L_0-H_0)\,\varphi (u)=0$ . If we define

\begin{align*} k = 6-5{\ell }-3m+4n_4+6n_6+8n_8+10n_{10}+12n_{12}+14n_{14}, \end{align*}

the above expression is rewritten as

(6.11) \begin{equation} \begin{aligned} \varphi (u_5,u_2,u_1)&=\sum b({\ell },m,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] &\ \ \ \ \ \cdot {\mu _4}^{n_4}\,{\mu _6}^{n_6}\,{\mu _8}^{n_8}\,{\mu _{10}}^{n_{10}}\, {\mu _{12}}^{n_{12}}\,{\mu _{14}}^{n_{14}}\, { \frac {{u_5}^{{\ell }}}{{\ell }!}\, \frac {{u_3}^m}{m!}\, \frac {{u_1}^k}{k!} }, \end{aligned} \end{equation}

where we require all the integer indices $k$ , $\ell$ , $m$ , $n_4$ , $n_6$ , $n_8$ , $n_{10}$ , $n_{12}$ , $n_{14}$ to be non-negative.

Note that the $u$ -weight of this expression is $k_0=6+4n_4+6n_6+8n_8+10n_{10}+12n_{12}+14n_{14}$ , which does not depend on $\ell$ or $m$ . (Note also that $k=k_0-5{\ell }-3m$ ). For fixed $n_4$ , $n_6$ , $n_8$ , $n_{10}$ , $n_{12}$ , $n_{14}\geq 0$ , $k_0\geq 0$ is fixed, and for non-negative $k$ , we require ${\ell }=0$ , $\ldots$ , $\lfloor (k_0+6)/5\rfloor$ , $m=0$ , $\ldots$ , $\lfloor (6+k_0-5{\ell })/3 \rfloor$ . As noted above, if we insert this ansatz into the equation for $(L_0-H_0)\varphi =0$ , we get an expression which is identically zero, for any set of $b({\ell },m,n_4,n_6,n_8,n_{10},n_{12},n_{14})$ .

If we insert this ansatz into the expression for $(L_2-H_2)\varphi =0$ , we get (after some algebra, and providing $k\gt 0$ ) the recurrence relation shown below, involving $20$ terms (compare the equations on p.68 of [8] for the genus 2 case). We can structure this relation by the weight of each $b$ coefficient of (6.11) (more precisely by the weight of the corresponding term in the expansion). We will call this $P_2$ :

\begin{align*} -7\,&b({{\ell }},m,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] +14(2-k)\,&b({{\ell }},m{+}1,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] -42m\,&b({{\ell }}{+}1,m{-}1,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] +196(n_{12}+1)\,&b({{\ell }},m,n_4,n_6,n_8,n_{10},n_{12}{+}1,n_{14}{-}1)\\[3pt] +168(n_{10}+1)\,&b({{\ell }},m,n_4,n_6,n_8,n_{10}{+}1,n_{12}{-}1,n_{14})\\[3pt] +140(n_8+1)\,&b({{\ell }},m,n_4,n_6,n_8{+}1,n_{10}{-}1,n_{12},n_{14})\\[3pt] +112(n_6+1)\,&b({{\ell }},m,n_4,n_6{+}1,n_8{-}1,n_{10},n_{12},n_{14})\\[3pt] -40(n_6+1)\,&b({{\ell }},m,n_4{-}2,n_6{+}1,n_8,n_{10},n_{12},n_{14})\\[3pt] +5(3-k)(2-k)\,&b({{\ell }},m,n_4{-}1,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] -8(n_{14}+1)\,&b({{\ell }},m,n_4{-}1,n_6,n_8,n_{10},n_{12}-1,n_{14}+1)\\[3pt] -16(n_{12}+1)\,&b({{\ell }},m,n_4{-}1,n_6,n_8,n_{10}{-}1,n_{12}{+}1,n_{14})\\[3pt] -24(n_{10}+1)\,&b({{\ell }},m,n_4{-}1,n_6,n_8{-}1,n_{10}{+}1,n_{12},n_{14})\\[3pt] -32(n_8+1)\,&b({{\ell }},m,n_4{-}1,n_6{-}1,n_8{+}1,n_{10},n_{12},n_{14})\\[3pt] +84(n_4+1)\,&b({{\ell }},m,n_4{+}1,n_6{-}1,n_8,n_{10},n_{12},n_{14})\\[3pt] -21m(m-1)\,&b({{\ell }},m{-}2,n_4,n_6,n_8{-}1,n_{10},n_{12},n_{14})\\[3pt] +8m(m-1)\,&b({{\ell }},m{-}2,n_4{-}2,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] +16m\,&b({{\ell }},m{-}1,n_4{-}1,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] -35{{\ell }}({{\ell }}{-}1)\,&b({{\ell }}{-}2,m,n_4,n_6,n_8,n_{10}, n_{12}{-}1,n_{14})\\[3pt] +4{{\ell }}({{\ell }}{-}1)\,&b({{\ell }}{-}2,m,n_4{-}1,n_6,n_8{-}1,n_{10}, n_{12},n_{14})\\[3pt] +8{{\ell }}\,&b({{\ell }}{-}1,m{+}1,n_4{-}1,n_6,n_8,n_{10},n_{12},n_{14})=0. \end{align*}

This relation applies only for $k\gt 1$ and can be written as

\begin{align*} P_2:\,&b(\ell, m,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] &=2\,(2-k)\,b(\ell, 1{+}m,n_4,n_6,n_8,n_{10},n_{12},n_{14}) \\[3pt] &\ \ \ -6m\,b(1{+}\ell, m{-}1,n_4,n_6,n_8,n_{10},n_{12},n_{14}) +\textrm {`` lower weight terms}'', \end{align*}

where the lower weight terms have coefficients which are quadratic or linear in $\ell$ , $m$ , $n_4$ , $n_6$ , $n_8$ , $n_{10}$ , $n_{12}$ , $n_{14}$ , times integers or rational numbers with denominators $7$ . Here the number $4n_4+6n_6+8n_8+10n_{10}+12n_{12}+14n_{14}$ for

\begin{align*} b({\ell },m,n_4,n_6,n_8,n_{10},n_{12},n_{14}) \end{align*}

is the $\mu$ weight of the term. For $P_2$ , the left-hand side and the first two terms on the right-hand side all have the $\mu$ -weight $W=4n_4+6n_6+8n_8+10n_{10}+12n_{12}+14n_{14}$ . The next highest $\mu$ -weight terms of the ‘lower weight terms’ are of $\mu$ -weight $W-2$ , and the lowest weight terms are of $\mu$ -weight $W-12$ .

Putting the same ansatz into $(L_4-H_4)\varphi =0$ we get another recurrence $P_4$ with $20$ terms, providing $m\gt 0$ and $k\gt 0$ . We can write this as

\begin{align*} P_4 : \,&b(\ell, 1+m,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] &= -7(k-1)\,b(1\,{+}\,\ell, m{-}1,n_4,n_6,n_8,n_{10},n_{12},n_{14})+\textrm {`` lower weight terms}''. \end{align*}

Here the lower weight terms have the same property as $P_2$ . We have another relation from the equation $(L_6-H_6)\varphi =0$

\begin{align*} P_6 :\,b(&\ell, m+2,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] &+2\,b(1+\ell, m,n_4,n_6,n_8,n_{10},n_{12},n_{14}) =\textrm {`` lower weight terms}''. \end{align*}

We can write this in two different ways which will each come in useful

\begin{align*} P_{6\mathrm {a}}&:\,b(l,m,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] &=-2\,b(l{+}1,m{-}2,n_4,n_6,n_8,n_{10},n_{12},n_{14}) +\textrm {`` lower weight terms}'',\\[3pt] P_{6\mathrm {b}}&: 2\,b(l,m,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] &=-b(l{-}1,m{+}2,n_4,n_6,n_8,n_{10},n_{12},n_{14}) +\textrm {`` lower weight terms}''. \end{align*}

Continuing, we have two further relations, from the equations $(L_8-H_8)\varphi =0$ and $(L_{10}-H_{10})\varphi =0$ ,

\begin{align*} \begin{aligned} P_8\ &: \ b({\ell }{+}1,m{+}1,n_4,n_6,n_8,n_{10},n_{12},n_{14}) =\textrm {`` lower} \mu -\textrm {weight terms}'', \\[3pt] P_{10}\ &: \ b({\ell }{+}2,m,n_4,n_6,n_8,n_{10},n_{12},n_{14}) =\textrm {`` lower} \mu -\textrm {weight terms}'', \\[3pt] \end{aligned} \end{align*}

where the lower $\mu$ -weight terms have the same properties as $P_2$ and $P_4$ . The relations $P_6$ , $P_8$ , $P_{10}$ have a total of $24$ , $24$ , $19$ terms respectively. As before, we need to normalise the expansion, so we choose $b(1,0,0,0,0,0,0,0)$ $=1$ . We need to find relations which either express coefficients in terms of ones with lower or equal $\mu$ -weight.

Clearly, we must take care with our recurrence relation to avoid infinite looping. We find that the following choice of recurrence scheme results in a sequence which decreases the $\mu$ -weight after no more than one extra step at any point in the recurrence :

\begin{align*} \begin{aligned} b(&{\ell },m,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] &=\begin{cases} \ 0 &\textrm {if }\ \textrm {min} \{k,{\ell },m,n_4,n_6,n_8,n_{10},n_{12},n_{14}\}\lt 0, \\[3pt] \ 1 &\textrm {if} {\ell }=1, m=n_4=n_6=n_8=n_{10}= n_{12}=n_{14}=0, \\[3pt] \ \mathrm {rhs}(P_2) &\textrm {if} \ k\gt 1, \\[3pt] \ \mathrm {rhs}(P_4) &\textrm {if} \ k=1, m\gt 0, \\[3pt] \ \mathrm {rhs}(P_{\mathrm {6a}}) &\textrm {if} \ k=1, m=0 \ ( and {\ell }\gt 0), \\[3pt] \ \mathrm {rhs}(P_{\mathrm {6b}}) &\textrm {if} \ k=0, m\gt 1,\\[3pt] \ \mathrm {rhs}(P_8) &\textrm {if} \ k=0, m=1 \ and {\ell }\gt 0,\\[3pt] \ \mathrm {rhs}(P_{10}) &\textrm {if} \ k=0, m=0 \ and {\ell }\gt 1. \end{cases} \end{aligned} \end{align*}

Note that the structure of this complicated linear recurrence relation does not depend on the moduli $\mu _i$ . We have used this to calculate the terms on the Hurwitz series for the solution up to weight 40 in $u_i$ (weight $34$ in the $\mu _i$ ). As for the $(2,5)$ -curve, there is another possible recursion scheme:

\begin{align*} b(&{\ell },m,n_4,n_6,n_8,n_{10},n_{12},n_{14})\\[3pt] &=\begin{cases} \ 0 & \textrm {if} \ \mathrm {min}\{k,{\ell },m,n_4,n_8,n_{10},n_{12},n_{14}\}\lt 0, \\[3pt] \ 1 & \textrm {if} \ \ {\ell }=1, m=n_4=n_8=n_{10}=n_{12}=n_{14}=0, \\[3pt] \ \mathrm {rhs}(P_{10}) & \textrm {if} \ {\ell }\gt 1,\\[3pt] \ \mathrm {rhs}(P_{8}) & \textrm {if} \ {\ell }=1, m\gt 0,\\[3pt] \ \mathrm {rhs}(P_{\mathrm {6a}}) & \textrm {if} \ {\ell }=1, m=0\ and\ k\gt 0,\\[3pt] \ \mathrm {rhs}(P_4) & \textrm {if} \ {\ell }=0, m\gt 0\ and\ k\gt 0,\\[3pt] \ \mathrm {rhs}(P_{\mathrm {6b}}) & \textrm {if} \ {\ell }=0, m\gt 0\ and\ k=0,\\[3pt] \ \mathrm {rhs}(P_2) & \textrm {if} \ {\ell }=0,\ and\ m= 0. \end{cases} \end{align*}

We have used this to calculate the terms in the series up to weight 40 in $\{u_j\}$ , or equivalently, weight 35 in the $\{\mu _i\}$ . The first few terms of the expansion are given as follows (up to a constant multiple):

\begin{align*} \varphi (u)=\sigma (u_5,&\ u_3,\ u_1) = 16\frac {{u_1}^6}{6!} - 2\frac {{u_1}^3u_3}{3!} - 2\frac {{u_3}^2}{2!} + {u_5 u_1} + 64\mu _4\frac {{u_1}^{10}}{10!} + 36 \mu _4 \frac {{u_1}^7u_3}{7!} \\[3pt] & - 4 \mu _4\frac {{u_1}^4{u_3}^2}{4!2!} - 2 \mu _4 \frac {u_1{u_3}^3}{3!} + 2 \mu _4\frac {u_5{u_1}^5}{5!} - 512 \mu _6\frac {{u_1}^{12}}{12!} + 64 \mu _6\frac {{u_1}^9u_3}{9!} \\[3pt] & + 16 \mu _6\frac {{u_1}^6{u_3}^2}{6!2!} - 8 \mu _6\frac {{u_1}^3{u_3}^3}{3!^2} - 8 \mu _6\frac {{u_3}^4}{4!} + 24 \mu _6\frac {u_5{u_1}^7}{7!}+\cdots . \end{align*}

Further studies are required to establish whether there are other recursion schemes which can be used to generate the series, and which recursions could be considered the most efficient in some sense.

6.7. The heat equations for the $(3,4)$ -curve

We take the trigonal genus three curve $\mathscr {C}=\mathscr {C}_{{\mu }}^{3,4}$ in the Weierstrass form

\begin{align*} y^3=(\mu _8+\mu _5 x+\mu _2 x^2)y + x^4+\mu _6 x^2+\mu _9 x +\mu _{12}. \end{align*}

The matrix $V$ is given by

\begin{align*} V=\underset {\substack {a\,\in \{0,3,4,6,7,10\}\\[3pt] b\,\in \{2,5,6,8,9,12\}}}{[V_{a,b}]} =\left [ \begin{array}{c@{\quad}c} V^{(1,1)} & V^{(1,2)}\\[3pt] {}^{t}{V^{(1,2)}} & V^{(2,2)} \end{array} \right ], \end{align*}

where

\begin{align*} \begin{aligned} V^{(1,1)}& =\left [ \begin{array}{c@{\quad}c@{\quad}c} 2\,\mu _2 & 5\,\mu _5 & 6\,\mu _6 \\[3pt] 5\,\mu _5 & \frac 16\,{\mu _2}^4-4\,\mu _2\mu _6+8\,\mu _8 & -\frac 12\,{\mu _2}^2\mu _5+9\,\mu _9 \\[3pt] 6\,\mu _6 & -\frac 12\,{\mu _2}^2\mu _5+9\,\mu _9 & \frac 23\,{\mu _2}^2\mu _6+\frac {10}3\,\mu _2\mu _8+\frac 53\,{\mu _5}^2 \end{array} \right ] \end{aligned} \end{align*}

and

\begin{align*} \begin{aligned} V^{(1,2)}&= \left [ \begin{array}{c@{\quad}c} 8\,\mu _8 & 9\,\mu _9 \\[5pt] \frac {1}{12}\,{\mu _2}^3\mu _5-\frac 12\,\mu _2\mu _9-\frac 32\,\mu _5\mu _6 & \frac 16\,{\mu _2}^3\mu _6{-}\frac 13\,{\mu _2}^2\mu _8{-} \frac 16\,\mu _2{\mu _5}^2{-}3\,{\mu _6}^2{+}12\,\mu _{12} \\[5pt] \frac 43\,{\mu _2}^2\mu _8-\frac 7{12}\,\mu _2{\mu _5}^2 +12\,\mu _{12} & \frac 43\,{\mu _2}^2\mu _{9} -\frac 76\,\mu _2\mu _5\mu _6+\frac {13}3\,\mu _5\mu _8 \end{array}\right . \\[3pt] &\hskip 100pt\left . \begin{array}{c} 12\,\mu _{12} \\[5pt] \frac 1{12}\,{\mu _2}^3\mu _9-\frac 16\,\mu _2\mu _5\mu _8-\frac 32\,\mu _6\mu _9\\[5pt] 2\,{\mu _2}^2\mu _{12}-\frac 7{12}\,\mu _2\mu _5\mu _9+\frac 83\,{\mu _8}^2 \end{array}\right ], \end{aligned} \end{align*}

and the remaining elements are

\begin{align*} V_{6,8} &=\frac 1{24}\,{\mu _2}^2{\mu _5}^2+6\,\mu _2\mu _{12}-\frac 72\,\mu _5\mu _9 +4\,\mu _6\mu _8,\\[3pt] V_{6,9} &= V_{5,4} = \frac 1{12}\,{\mu _2}^2\mu _5\mu _6 +\frac 76\,\mu _2\mu _5\mu _8-\frac {5}{12}\,{\mu _5}^3 -\frac 32\,\mu _6\mu _9,\\[3pt] V_{6,10} &= V_{6,4}= \frac 1{24}\,{\mu _2}^2\mu _5\mu _9 +\frac 43\,\mu _2{\mu _8}^2 -\frac 5{12}\,{\mu _5}^2\mu _8+6\,\mu _6\mu _{12}-\frac 94\,{\mu _9}^2,\\[3pt] V_{7,9} &=\frac 16\,{\mu _2}^2{\mu _6}^2+2\,{\mu _2}^{2}\mu _{12} +\frac 53\,\mu _2\mu _5\mu _9 -\frac 83\,\mu _2\mu _6\mu _8-\frac 43\,{\mu _5}^2\mu _6 +\frac 83\,{\mu _8}^2,\\[3pt] V_{7,12} &=V_{6,5}=\frac 1{12}\,{\mu _2}^2\mu _6\mu _9+3\,\mu _2\mu _5\mu _{12} -\frac 56\,\mu _2\mu _8\mu _9-\frac 5{12}\,{\mu _5}^2\mu _9 -\frac 12\,\mu _5\mu _6\mu _8,\\[3pt] V_{10,12} &=\frac 1{24}\,{\mu _2}^2{\mu _9}^2+2\,\mu _2\mu _8\mu _{12} +{\mu _5}^2\mu _{12} -\frac {11}{6}\,\mu _5\mu _8\mu _9 +\frac 43\,\mu _6{\mu _8}^2. \end{align*}

The discriminant $\varDelta$ of $\mathscr {C}$ is calculated by Maple along 1.5, has $670$ terms and is of weight $72$ . The result shows $\varDelta =3^3\,{\cdot }\,4^2\,{\cdot }\,\det (V)$ . Now, after a calculation by Maple (which shows 5.41), we have

\begin{align*} {[\,{L}_0\, {L}_3\, {L}_4\, {L}_6\, {L}_7\, {L}_{10}]}\,\varDelta =[\,72\ \ 0\,\ -8{\mu _2}^2\,\ 12\mu _6\,\ -8\mu _2\mu _5\,\ -{\mu _5}^2-4\mu _2\mu _8\,]\varDelta . \end{align*}

As in the $(2,7)$ -case, we have fundamental relations for these ${L}_i$ as a set of generators of certain Lie algebra. The symplectic basis of $H_{\mathrm {dR}}^1(\mathscr {C}/\mathbb {Q}[{\mu }])$ in this case is given by

\begin{align*} \omega _{5}=\frac {dx}{3y^2}, \ \omega _{2}=\frac {xdx}{3y^2}, \ \omega _{1}=\frac {ydx}{3y^2}, \ \eta _{-5}=\frac {5x^2ydx}{3y^2}, \ \eta _{-2}=\frac {2xydx}{3y^2}, \ \eta _{-1}=\frac {x^2dx}{3y^2}. \end{align*}

The matrices $\Gamma _j=\bigg [ \begin{array}{c@{\quad}c} -\beta _j &\ \alpha _j \\[3pt] -\gamma _j & {}^{t}{\beta _j}\end{array} \bigg ]$ are given as follows ³ :

\begin{align*} \alpha _0&=O, \ \ \beta _0=\left [ \begin{array}{c@{\quad}c@{\quad}c} 5 & & \\[3pt] & 2 & \\[3pt] & & 1 \end{array} \right ], \ \ \gamma _0=O, \\[3pt] \alpha _3&= \left [ \begin{array}{c@{\quad}c@{\quad}c} \ \ & & \\[3pt] & & 1 \\[3pt] & 1 & \end{array} \right ], \quad \beta _3 = \left [ \begin{array}{c@{\quad}c@{\quad}c} & 2 & \\[3pt] \frac 1{12}\,{\mu _2}^3-\frac 32\,\mu _6 & & -\frac 12\,\mu _2 \\[3pt] -\frac 16\,\mu _5\mu _2 & -\frac 13\,{\mu _2}^2 & \end{array} \right ], \\[3pt] \gamma _3&= \left [ \begin{array}{c@{\quad}c@{\quad}c} 5\,\mu _5\mu _8-\frac 13\,{\mu _2}^2 \mu _9+\frac 1{12}\,{\mu _2}^4\mu _5 -\frac 53\,\mu _2\mu _5\mu _6 & -\mu _2\mu _8 & \mu _9 \\[3pt] -\mu _2\mu _8 & \frac 23\,\mu _5\mu _2 & \frac 16\,{\mu _2}^3 -\mu _6 \\[3pt] \mu _9 & \frac 16\,{\mu _2}^3-\mu _6 & \mu _5 \end{array} \right ], \\[3pt] \alpha _4& =\left [ \begin{array}{c@{\quad}c@{\quad}c} \ \ & & \\[3pt] & 1 & \\[3pt] & &\frac 13\,\mu _2 \end{array} \right ], \ \ \beta _4= \left [ \begin{array}{c@{\quad}c@{\quad}c} \frac 23\,{\mu _2}^2 & & 1 \\[3pt] -\frac 7{12}\,\mu _5\mu _2 & & \\[3pt] \frac 53\,\mu _8 & \frac 23\,\mu _5 & \end{array} \right ], \\[3pt] \gamma _4&= \left [ \begin{array}{c@{\quad}c@{\quad}c} -\frac 7{12}\,{\mu _2}^2{\mu _5}^2+9\,\mu _2\mu _{12} +\frac 53\,\mu _5\mu _9+\frac {11}3\,\mu _6\mu _8 & \frac 23\,\mu _2\mu _9 & -\frac 13\,\mu _2\mu _8 \\[3pt] \frac 23\,\mu _2\mu _9 & \frac 43\,\mu _2\mu _6 +\frac 43\,\mu _8 & -\frac 12\,\mu _5\mu _2 \\[3pt] -\frac 13\,\mu _2\mu _8 & -\frac 12\,\mu _5\mu _2 & \mu _6 \end{array} \right ], \\[3pt] \alpha _6 &= \left [ \begin{array}{c@{\quad}c@{\quad}c} & \ \ & 1 \\[3pt] & & \\[3pt] 1 & & \end{array} \right ], \quad \beta _6= \left [ \begin{array}{c@{\quad}c@{\quad}c} \mu _6 & & \\[3pt] \frac 1{24}\,{\mu _2}^2\mu _5 -\frac 54\,\mu _9 & & -\frac 14\,\mu _5 \\[3pt] \frac 13\,\mu _2\mu _8-\frac 5{12}\,{\mu _5}^2 & -\frac 16\,\mu _5\mu _2 & \end{array} \right ], \\[3pt] \gamma _6 &= \left [ \begin{array}{c@{\quad}c@{\quad}c} \left \{\ \substack { \frac 1{24}\,{\mu _2}^3{\mu _5}^2 +4\,{\mu _2}^2\mu _{12} -\frac {29}{12}\,\mu _2\mu _5\mu _9\\[3pt] +\frac 43\,\mu _2\mu _6\mu _8-\frac 5{12}\,{\mu _5}^2\mu _6 +6\,{\mu _8}^2} \ \right \} & \frac 12\,\mu _5\mu _8 & 3\,\mu _{12} \\[8pt] \frac 12\,\mu _5\mu _8 & \frac 83\,\mu _2\mu _8 -\frac 13\,{\mu _5}^2 & \frac 1{12}\,{\mu _2}^2\mu _5 -\frac 12\,\mu _9 \\[3pt] 3\,\mu _{12} & \frac 1{12}\,{\mu _2}^2\mu _5-\frac 12 \,\mu _9 & 2\,\mu _8 \end{array} \right ], \\[3pt] \alpha _7 &= \left [ \begin{array}{c@{\quad}c@{\quad}c} & 1 & \\[3pt] 1 & & \\[3pt] & & \frac 13\,\mu _5 \end{array} \right ], \ \ \beta _7= \left [ \begin{array}{c@{\quad}c@{\quad}c} \frac 23\,\mu _5\mu _2 & & \\[3pt] \frac 1{12}\,{\mu _2}^2\mu _6-\frac 76\,\mu _2\mu _8 -\frac {5\,{\mu _5}^2}{12} & & -\frac 12\,\mu _6 \\[3pt] \frac 13\,\mu _2\mu _9 -\frac 12\,\mu _5\mu _6 & -\frac 13\,\mu _2\mu _6 +\frac 23\,\mu _8 & \end{array} \right ], \\[3pt] \gamma _7 &=\left [ \begin{array}{c@{\quad}c@{\quad}c} \gamma _7^{[1,1]} & 2\,\mu _2\mu _{12}+\frac 23\,\mu _5\mu _9-\mu _6\mu _8 & \frac 23\,\mu _5\mu _8 \\[3pt] 2\,\mu _2\mu _{12} +\frac 23\,\mu _5\mu _9-\mu _6\mu _8 & \frac 83\,\mu _2\mu _9 -\frac 23\,\mu _5\mu _6 & -\frac 16\,{\mu _5}^2 +\frac 16\,{\mu _2}^2\mu _6-\frac 13\,\mu _2\mu _8 \\[3pt] \frac 23\,\mu _5\mu _8 & -\frac 16\,{\mu _5}^2 +\frac 16\,{\mu _2}^2\mu _6-\frac 13\,\mu _2\mu _8 & 2\,\mu _9 \end{array} \right ],\\[3pt] & \big (\,\gamma _7^{[1,1]} = -\tfrac 5{12}\,\mu _2{\mu _5}^3 -\tfrac 12\,\mu _5{\mu _6}^2 +5\,\mu _{12}\mu _5 +\tfrac {14}3\,\mu _8 \mu _9 +\tfrac 1{12}\,{\mu _2}^3\mu _5\mu _6 -\tfrac 16\,{\mu _2}^2\mu _5\mu _8 -\mu _2\mu _6\mu _9\,\big ), \end{align*}

\begin{align*} \alpha _{10}& = \left [ \begin{array}{c@{\quad}c@{\quad}c} 1 & \ \ & \\[3pt] & & \\[3pt] & & \frac 13\,\mu _8 \end{array} \right ], \ \ \beta _{10}= \left [ \begin{array}{c@{\quad}c@{\quad}c} -\frac 13\,\mu _2\mu _8 & & \\[3pt] \frac 1{24}\,{\mu _2}^2\mu _9 -\frac 5{12}\,\mu _5\mu _8 & & -\frac 14\,\mu _9 \\[3pt] \mu _2\mu _{12}-\frac 5{12}\,\mu _5\mu _9 +\frac 13\,\mu _6\mu _8 & -\frac 16\,\mu _2\mu _9 & \end{array} \right ], \\[6pt] \gamma _{10}&= \left [ \begin{array}{c@{\quad}c@{\quad}c} \gamma _{10}^{[1,1]} & 2\,\mu _{12}\mu _5 -\frac 56\,\mu _8\mu _9 & \frac 23\,{\mu _8}^2 \\[3pt] 2\,\mu _{12}\mu _5-\frac 56\,\mu _8\mu _9 & 4\,\mu _2\mu _{12}-\frac 13\,\mu _5\mu _9 & -\frac 16\,\mu _5\mu _8+\frac 1{12}\,{\mu _2}^2\mu _9 \\[3pt] \frac 23\,{\mu _8}^2 & -\frac 16\,\mu _5\mu _8+\frac 1{12}\,{\mu _2}^2\mu _9 & 3\,\mu _{12} \end{array} \right ], \\[6pt] & \left(\,\gamma _{10}^{[1,1]} =\tfrac 1{24}\,{\mu _2}^3\mu _5\mu _9+{\mu _2}^2{\mu _8}^2 -\tfrac 5{12}\,\mu _2{\mu _5}^2\mu _8 +3\,\mu _2\mu _6\mu _{12} -\tfrac 76\,\mu _2{\mu _9}^2 \right.\\[3pt] &\hskip 150pt \left.-\tfrac {5}{12}\,\mu _5\mu _6\mu _9 +\tfrac 13\,{\mu _6}^2\mu _8 +9\,\mu _8\mu _{12}\,\right). \end{align*}

6.8. The sigma function for the $(3,4)$ -curve

Following [8] and from the conditions IC1, IC2 of (5.59), but using the Hurwitz series form, the sigma function is of the form

\begin{align*} \sigma &(u_5,u_2,u_1) =\sum _{\ell, m,n_2,n_5,n_6,n_8,n_9,n_{12}}\Big [\,b(\ell, m,n_2,n_5,n_6,n_8,n_9,n_{12})\, {u_1}^5\left (\frac {u_5}{{u_1}^5} \right )^{\ell }\\[3pt] &\cdot \left (\frac {u_2}{{u_1}^2}\right )^{m} \left (\mu _2{u_1}^2\right )^{n_2} \left (\mu _5{u_1}^5\right )^{n_5} \left (\mu _6{u_1}^6\right )^{n_6} \left (\mu _8{u_1}^8\right )^{n_8} \left (\mu _9{u_1}^9\right )^{n_9} \left (\mu _{12}{u_1}^{12}\right )^{n_{12}}\\[3pt] &\hskip 40pt\big /\big (\,\ell !\,m!\,(5-5\ell -2m+2n_2+5n_5+6n_6+8n_8 +9n_9+12n_{12})!\,\big )\Big ]. \end{align*}

for the $(3,4)$ -curve. If we define

\begin{align*} k=5-5\ell -2m+2n_2+5n_5+6n_6+8n_8+9n_9+12n_{12}, \end{align*}

we can rewrite the above expression as

\begin{align*} \begin{aligned} \sigma (u_5,u_2,u_1) =\sum \,b(\ell, &m,n_2,n_5,n_6,n_8,n_9,n_{12})\\[3pt] &\cdot \frac {{\mu _2}^{n_2} {\mu _5}^{n_5} {\mu _6}^{n_6} {\mu _8}^{n_8} {\mu _9}^{n_9} {\mu _{12}}^{n_{12}} \,{u_5}^{\ell } {u_2}^m {u_1}^k} {\ell !\,m!\,k!}, \end{aligned} \end{align*}

where we require all the integer indices $k$ , $\ell$ , $m$ , $n_2$ , $n_5$ , $n_6$ , $n_8$ , $n_9$ , $n_{12}$ to be non-negative. Note that the $u$ -weight of this expression is $k_0=5+2n_2+5n_5+6n_6+8n_8+9n_9+10n_{12}$ , which does not depend on $\ell$ or $m$ . (Note also that $k=k_0-5\ell -2m$ .) For fixed $n_2$ , $n_5$ , $n_8$ , $n_6$ , $n_9$ , $n_{12}\ge 0$ , $k_0\ge 0$ is fixed, and for non-negative $k$ , we require $\ell =0$ , $\ldots$ , $\lfloor k_0/5\rfloor$ , $m=0$ , $\ldots$ , $\lfloor (k_0-5\ell )/2 \rfloor$ . In addition, we can use the condition that $\sigma$ is an odd function, $\sigma ({-}u)=-\sigma (u)$ ; this tells us that if $k_0$ is even(odd) then we should restrict ourselves to $m$ even(odd) respectively.

If we insert this ansatz into the equation for $(L_0-H_0)\sigma =0$ , we get an expression which is identically zero, whatever the values for the $b(\ell, m,n_2,n_5,n_6,n_8,n_9,n_{12})$ . If we insert the ansatz into the equation for $(L_3-H_3)\sigma =0$ , we get (after some algebra) the recurrence relation shown below, involving 34 terms (compare the equations on p.68 of [8] for the genus 2 case). We can structure the relation by the weight of each $b$ coefficient (more precisely by the weight of the corresponding term in the sigma expansion).

Contrarily to the $(2,3)$ -, $(2,5)$ -, $(2,7)$ -curves, we could not find any approach for the $(3,4)$ -curve to prove Hurwitz integrality of the expansion of $\sigma (u)$ .

We call the recurrence relation, generated from $(L_3\,{-}\,H_3)\sigma =0$ , $R_3$ :

\begin{align*} 24\,b({\ell },m+1,n_2,&n_5,n_6,n_8,n_9,n_{12})\\[3pt] &+48m\,b({\ell }+1,m-1, n_2,n_5,n_6,n_8,n_9,n_{12}) \\[3pt] =-12(4-k)(3-k)&\,b({\ell },m,n_2,n_5-1,n_6,n_8,n_9,n_{12}) \\[3pt] -36(n_8+1)&\,b({\ell },m,n_2,n_5-1,n_6-1,n_8+1,n_9,n_{12}) \\[3pt] +4(n_9+1)&\,b({\ell },m,n_2-3,n_5,n_6-1,n_8,n_9+1,n_{12}) \\[3pt] +2(n_{12}+1)&\,b({\ell },m,n_2-3,n_5,n_6,n_8,n_9-1,n_{12}+1)\\[3pt] +4(n_5+1)&\,b({\ell },m,n_2-4,n_5+1,n_6,n_8,n_9,n_{12}) \\[3pt] -8(n_9+1)&\,b({\ell },m,n_2-2,n_5,n_6,n_8-1,n_9+1,n_{12}) \\[3pt] +2(n_8+1)&\,b({\ell },m,n_2-3,n_5-1,n_6,n_8+1,n_9,n_{12}) \\[3pt] -96(n_5+1)&\,b({\ell },m,n_2-1,n_5+1,n_6-1,n_8,n_9,n_{12}) \\[3pt] -12(n_8+1)&\,b({\ell },m,n_2-1,n_5,n_6,n_8+1,n_9-1,n_{12}) \\[3pt] -12(n_6+1)&\,b({\ell },m,n_2-2,n_5-1,n_6+1,n_8,n_9,n_{12}) \\[3pt] -4(n_{12}+1)&\,b({\ell },m,n_2-1,n_5-1,n_6,n_8-1,n_9,n_{12}+1) \\[3pt] -4(n_9+1)&\,b({\ell },m,n_2-1,n_5-2,n_6,n_8,n_9+1,n_{12}) \\[3pt] +120(n_2+1)&\,b({\ell },m,n_2+1,n_5-1,n_6,n_8,n_9,n_{12}) \\[3pt] -12(3-k)&\,\underline {b({\ell },m+1,n_2-1,n_5,n_6,n_8,n_9,n_{12})} \\[3pt] -24m(3-k)&\,b({\ell },m-1,n_2,n_5,n_6-1,n_8,n_9,n_{12}) \\[3pt] -8m(m-1)&\,b({\ell },m-2,n_2-1,n_5-1,n_6,n_8,n_9,n_{12}) \\[3pt] +24{\ell }(3-k)&\,b({\ell }-1,m,n_2,n_5,n_6,n_8,n_9-1,n_{12}) \\[3pt] -60{\ell }({\ell }-1)&\,b({\ell }-2,m,n_2,n_5-1,n_6,n_8-1,n_9,n_{12}) \\[3pt] +4m(3-k)&\,b({\ell },m-1,n_2-3,n_5,n_6,n_8,n_9,n_{12}) \\[3pt] -{\ell }({\ell }-1)&\,b({\ell }-2,m,n_2-4,n_5-1,n_6,n_8,n_9,n_{12}) \\[3pt] +4{\ell }({\ell }-1)&\,b({\ell }-2,m,n_2-2,n_5,n_6,n_8,n_9-1,n_{12}) \\[3pt] +20{\ell }({\ell }-1)&\,b({\ell }-2,m,n_2-1,n_5-1,n_6-1,n_8,n_9,n_{12}) \\[3pt] +24{\ell }m&\,b({\ell }-1,m-1,n_2-1,n_5,n_6,n_8-1,n_9,n_{12}) \\[3pt] +8m&\,b({\ell },m-1,n_2-2,n_5,n_6,n_8,n_9,n_{12}) \\[3pt] +4{\ell }&\,b({\ell }-1,m,n_2-1,n_5-1,n_6,n_8,n_9,n_{12}) \\[3pt] -2{\ell }&\,b({\ell }-1,m+1,n_2-3,n_5,n_6,n_8,n_9,n_{12}) \\[3pt] +36{\ell }&\,b({\ell }-1,m+1,n_2,n_5,n_6-1,n_8,n_9,n_{12}) \\[3pt] -36(n_{12}+1)&\,b({\ell },m,n_2,n_5,n_6-1,n_8,n_9-1,n_{12}+1) \\[3pt] -72(n_9+1)&\,b({\ell },m,n_2,n_5,n_6-2,n_8,n_9+1,n_{12}) \\[3pt] +288(n_9+1)&\,b({\ell },m,n_2,n_5,n_6,n_8,n_9+1,n_{12}-1)\\[3pt] +192(n_5+1)&\,b({\ell },m,n_2,n_5+1,n_6,n_8-1,n_9,n_{12}) \\[3pt] +216(n_6+1)&\,b({\ell },m,n_2,n_5,n_6+1,n_8,n_9-1,n_{12}). \end{align*}

Note the two expressions on the left-hand side, which are the highest weight terms, at weight $W=2n_2+5n_5+6n_6+8n_8+9n_9+12n_{12}$ . The next highest weight term (underlined) is of weight $W-2$ , and the lowest weight terms are of weight $W-13$ . Putting the ansatz into the equation for $(L_4-H_4)\sigma$ we get another recurrence with 27 terms, which we call $R_4$ :

\begin{align*} -12\,b({\ell },m+2,n_2,&n_5,n_8,n_6,n_9,n_{12})\\[3pt] &+24(4-k)\,b({\ell }+1,m,n_2,n_5,n_6,n_8,n_9,n_{12}) \\[3pt] =4&\,\underline {b({\ell },m,n_2-1,n_5,n_6,n_8,n_9,n_{12})} \\[3pt] +16{\ell }m&\,b({\ell }-1,m-1,n_2-1,n_5,n_6,n_8,n_9-1,n_{12}) \\[3pt] -14{\ell }&\,b({\ell }-1,m+1,n_2-1,n_5-1,n_6,n_8,n_9,n_{12}) \\[3pt] +40{\ell }&\,b({\ell }-1,m,n_2,n_5,n_6,n_8-1,n_9,n_{12}) \\[3pt] +16m&\,b({\ell },m-1,n_2,n_5-1,n_6,n_8,n_9,n_{12}) \\[3pt] -7{\ell }({\ell }-1)&\,b({\ell }-2,m,n_2-2,n_5-2,n_6,n_8,n_9,n_{12}) \\[3pt] +108{\ell }({\ell }-1)&\,b({\ell }-2,m,n_2-1,n_5,n_6,n_8,n_9,n_{12}-1) \\[3pt] +44{\ell }({\ell }-1)&\,b({\ell }-2,m,n_2,n_5,n_8-1,n_6-1,n_9,n_{12}) \\[3pt] +12(5-k)(4-k)&\,b({\ell },m,n_2,n_5,n_6-1,n_8,n_9,n_{12}) \\[3pt] +8{\ell }(4-k)&\,b({\ell }-1,m,n_2-1,n_5,n_6,n_8-1,n_9,n_{12}) \\[3pt] +20{\ell }({\ell }-1)&\,b({\ell }-2,m,n_2,n_5-1,n_6,n_8,n_9-1,n_{12}) \\[3pt] -288(n_8+1)&\,b({\ell },m,n_2,n_5,n_6,n_8+1,n_9,n_{12}-1) \\[3pt] -64(n_{12}+1)&\,b({\ell },m,n_2,n_5,n_6,n_8-2,n_9,n_{12}+1) \\[3pt] -40(n_6+1)&\,b({\ell },m,n_2,n_5-2,n_6+1,n_8,n_9,n_{12}) \\[3pt] -216(1+n_5)&\,b({\ell },m,n_2,n_5+1,n_6,n_8,n_9-1,n_{12}) \\[3pt] -80(n_6+1)&\,b({\ell },m,n_2-1,n_5,n_6+1,n_8-1,n_9,n_{12}) \\[3pt] -4(\ell -1-n_9-8&n_5-2n_6+k+2m-2n_2)\\[3pt] \cdot &\,b({\ell },m,n_2-2,n_5,n_6,n_8,n_9,n_{12}) \\[3pt] -104(n_9+1)&\,b({\ell },m,n_2,n_5-1,n_6,n_8-1,n_9+1,n_{12}) \\[3pt] +14(n_8+1)&\,b({\ell },m,n_2-1,n_5-2,n_6,n_8+1,n_9,n_{12}) \\[3pt] +14(n_{12}+1)&\,b({\ell },m,n_2-1,n_5-1,n_6,n_8,n_9-1,n_{12}+1) \\[3pt] +28(n_9+1)&\,b({\ell },m,n_2-1,n_5-1,n_6-1,n_8,n_9+1,n_{12}) \\[3pt] -144(n_2+1)&\,b({\ell },m,n_2+1,n_5,n_6-1,n_8,n_9,n_{12}) \\[3pt] +16m(m-1)&\,b({\ell },m-2,n_2,n_5,n_6,n_8-1,n_9,n_{12}) \\[3pt] +16m(m-1)&\,b({\ell },m-2,n_2-1,n_5,n_6-1,n_8,n_9,n_{12}) \\[3pt] +12m(4-k)&\,b({\ell },m-1,n_2-1,n_5-1,n_6,n_8,n_9,n_{12}). \end{align*}

As for $R_3$ , the two expressions on the left-hand side, are the highest weight terms, at weight $W=2n_2+5n_5+6n_6+8n_8+9n_9+12n_{12}$ . The next highest weight terms are of weight $W-2$ , and the lowest weight terms are of weight $W-14$ .

We see that the two recurrence relations have the same terms in $b$ . Hence we can take linear combinations to get two relations, each with only one leading term at weight $W$

\begin{align*} S_{3,4}: \,b(\ell, m, n_2, n_5, n_8, n_6, n_9, n_{12}) & =\frac 1{k-m+1} \left (\text {lower weight terms}\right )\ \,(m\neq 0),\\[3pt] T_{3,4}: \,b(\ell, m, n_2, n_5, n_8, n_6, n_9, n_{12}) & =\frac 1{k-m}\left (\text {lower weight terms}\right ) \ \ (l\neq 0). \end{align*}

These $S_{3,4}$ and $T_{3,4}$ connect the left-hand side with terms of relative weight $-2$ and lower, down to $-14$ . In addition we have other relations from the equations $(L_6-H_6)\sigma =0$ , $(L_7-H_7)\sigma =0$ , and $(L_{10}-H_{10})\sigma =0$ that

\begin{align*} R_6: \,b(\ell, m, n_2, n_5, n_8, n_6, n_9, n_{12}) & = \textrm {`` lower weight terms}'',\\[3pt] R_7: \ b(\ell, m, n_2, n_5, n_8, n_6, n_9, n_{12}) & = \textrm {`` lower weight terms}'',\\[3pt] R_{10}: \ b(\ell, m, n_2, n_5, n_8, n_6, n_9, n_{12}) & = \textrm {`` lower weight terms}'', \end{align*}

respectively. Here the right-hand sides are linear in the coefficients $b$ with coefficients at most quadratic in $k$ , $\ell$ , $m$ , $n_2$ , $n_5$ , $n_8$ , $n_6$ , $n_9$ , $n_{12}$ over the rationals but each denominator is a divisor of $24$ .

$R_6$ , $R_7$ , $R_{10}$ have a total of 37, 47, 42 terms respectively and connect the left-hand side with terms of relative weight $-5$ , $-5$ , $-8$ and lower, down to $-16$ , $-17$ , $-20$ respectively.

Ideally, we would like to proceed as follows. Suppose we have already calculated the $b$ coefficients at weight $W-2$ . Then we would like to use one of the above to calculate each coefficient at weight $W$ . We could proceed in this manner to calculate coefficients at successive weight levels to the required number of terms. However, this approach needs some modification. Recall that the weight does not depend on $\ell$ or $m$ . Clearly if $\ell \gt 1$ we can use $R_6$ , and if $\ell =1$ , $m\gt 0$ , we can use $R_7$ . Similarly if $\ell =1$ , $k\gt 0$ , we can use $R_6$ . A short calculation shows that if $\ell =1$ , one of these two possibilities holds except in the special case $\ell =1$ , $m=n_2=n_5=n_8=n_6=n_9=n_{12}=0$ which is covered later. For the case $\ell =0$ we cannot use $R_6$ , $R_7$ , $R_{12}$ . If $m\ne 0$ and $m\ne (k+1)$ we can use $S_{3,4}$ . All the possibilities considered so far will reduce the weight by 2. There remain the cases $m=0$ and $m=(k+1)$ to deal with.

The case $\ell =0$ , $m=0$ is handled as follows. Take $48(k-m)\,T_{3,4}$ :

\begin{align*} 48&(m-k)\,b({\ell },m,n_2,n_5,n_6,n_8,n_9,n_{12})\\[3pt] &=8\,b({\ell }-1,m,n_2-1,n_5,n_6,n_8,n_9,n_{12})\\[3pt] &\ \ \ \ +12k\,b({\ell }-1,m+2,n_2,n_5,n_6,n_8,n_9,n_{12})+\cdots . \end{align*}

Shifting by $n_2\,{\rightarrow }\,n_2\,{+}\,1$ , the first term in the right-hand side is expressed as

\begin{align*} b({\ell }-1,&m,n_2,n_5,n_6,n_8,n_9,n_{12})\\[3pt] &=-6(m-k-2)\,b({\ell },m,n_2+1,n_5,n_6,n_8,n_9,n_{12})\\[3pt] &\quad -\tfrac 32(k+2)\,b({\ell }-1,m+2,n_2,n_5,n_6,n_8,n_9,n_{12})+\cdots . \end{align*}

On the right-hand side, we now have two terms of non-negative relative weight as above of relative weight $+2$ which comes from the underlined term in $R_3$ and of relative weight $0$ which comes from the underlined term in $R_4$ . Putting $\ell =1$ , $m=0$ , we have, say $T_{3,4}^{(0)}$ , that

\begin{align*} b(&0,0,n_2,n_5,n_6,n_8,n_9,n_{12})\\[3pt] &=-6\,(k-3+5\,\ell +2\,m)\, b(1,0,n_2+1,n_5,n_6,n_8,n_9,n_{12})\\[3pt] &\qquad -\tfrac 32\,(k-3+5\,\ell +2\,m)\,b(0,2,n_2,n_5,n_6, n_8,n_9,n_{12})+\cdots . \end{align*}

The first term in the right-hand side has $\ell =1$ , $m=0$ , and $k=5+2n_2+\ldots \gt 0$ . Hence, we can apply $R_7$ to this term to give a term with maximum relative weight $+2-5=-3$ . The second term has $\ell =0$ , $m=2$ , and $k=1+2n_2+5n_5+\cdots$ so $k+1\gt 2$ and hence $k+1\ne m$ . For this term, we can apply $S_{3,4}$ to produce a term of maximum relative weight $0-2=-2$ . Hence both terms of weight $\geq 0$ can be expressed as terms of relative weight $\leq -2$ , so our chain eventually decreases in weight. The case $\ell =0$ , $m=(k+1)$ is treated as follows. Take $R_3$ , shift by $m\rightarrow m-1$ , and set $\ell =0$ to get

\begin{align*} R_3^{(0)}: \ &b(0,m,n_2,n_5,n_6,n_8,n_9,n_{12})\\[3pt] &=-2(m-1)\,b(1,m-2,n_2,n_5,n_6,n_8,n_9,n_{12}) +\textrm {`` lower weight terms}^{\prime\prime}. \end{align*}

Now the first term on the right, $b(1,m-2,n_2,n_5,n_6,n_8,n_9,n_{12})$ , is of the same weight as the term on the left. Write this as

\begin{align*} b(1,m^{\prime},n_2,n_5,n_6,n_8,n_9,n_{12}), \end{align*}

with corresponding $k$ -value $k^{\prime}$ . If $\mathrm {min}(k^{\prime}, m^{\prime})\lt 0$ then this term is zero as discussed above. If $k^{\prime}=0$ , $m^{\prime}=0$ , it is easy to show that $m^{\prime}=n_2=n_5=n_8=n_6=n_9=n_{12}=0$ , and this term $b(1,0,0,0,0,0,0,0)$ cannot be reduced further. Otherwise one or both of $k^{\prime}=0$ , $m^{\prime}$ is positive, so we can apply $R_7$ or $R_6$ to reduce the term to terms of relative weight $\leq -2$ , so our chain terminates or decreases in weight. These choices, plus the requirement discussed above that $b(\ell, m,n_2,n_5,n_6,n_8,n_9,n_{12})=0$ if any of the $\{k,\ell, m,n_2,n_5,n_6,n_8,n_9,n_{12}\}$ are negative, define all the $b(\ell, m,n_2,n_5,n_6,n_8,n_9,n_{12})$ in terms of the so-far undefined $b(1,0,0,0,0,0,0,0)$ . Therefore the solution of the system

\begin{align*} (L_j-H_j)\sigma (u)=0\ \ (j=0,\ 3,\ 4,\ 6,\ 7,\ 10) \end{align*}

is of dimension one. Choosing $b(1,0,0,0,0,0,0,0)=1$ , we summarise with $k=5-5\ell -2m+2n_2+5n_5+8n_8+6n_6+9n_9+12n_{12}$ as defined as above as follows:

\begin{align*} \begin{aligned} b(\ell, &m, n_2,n_5, n_8, n_6, n_9, n_{12}) = \\[3pt] &=\begin{cases} \ 0 & \quad \textrm {if} \ \mathrm {min}(k,\ell, m,n_2,n_5,n_6,n_8,n_9,n_{12})\lt 0, \\[3pt] \ 1 & \quad \textrm {if} \ \ell =1, m=n_2=n_5=n_8=n_6=n_9=n_{12}=0, \\[3pt] \ \mathrm {rhs}(R_{10}) & \quad \textrm {if} \ \ell \gt 1,\\[3pt] \ \mathrm {rhs}(R_7) & \quad \textrm {if} \ \ell \gt 0, m\gt 0,\\[3pt] \ \mathrm {rhs}(R_6) & \quad \textrm {if} \ \ell \gt 0, k\gt 0,\\[3pt] \ \mathrm {rhs}(S_{3,4}) & \quad \textrm {if} \ \ell =0, m\ne 0 and m\ne (k+1),\\[3pt] \ \mathrm {rhs}(T_{3,4}^{(0)}) & \quad \textrm {if} \ l=m=0,\\[3pt] \ \mathrm {rhs}(R_3^{(0)}) & \quad \textrm {if} \ \ell =0 and m=(k+1). \end{cases} \end{aligned} \end{align*}

We have used this to calculate the terms in the sigma series up to weight 40 in $\{u_j\}$ , or equivalently, weight 35 in the $\{\mu _i\}$ . The first few terms of the sigma expansion are given as follows (up to a constant multiple):

\begin{align*} \sigma ({u_5}&,{u_2},{u_1}) = {u_5}+\frac {6\,u_1^5}{5!} -2\frac {u_1{u_2}^2}{2!} -2\mu _2\frac {u_1^3{u_2}^2}{2!\,3!} +30\mu _2\frac {{u_1}^7}{7!} -2{\mu _2}^2\frac {u_1{u_2}^4}{4!}\\[3pt] &-2{\mu _2}^2\frac {{u_1}^5{u_2}^2}{2!\,5!} +126\,{\mu _2}^2\frac {{u_1}^9}{9!} +24\mu _5\frac {{u_1}^8u_2}{8!} -\mu _5\frac {u_5u_2{u_1}^3}{3!} +8\mu _5\frac {{u_2}^5}{5!}\\[3pt] &-2\mu _6\frac {2\,u_5{u_2}^2{u_1}^2}{2!\,2!} +6\mu _6\frac {u_5{u_1}^6}{6!} +24\mu _6\frac {{u_1}^7{u_2}^2}{2!\,7!} -2{\mu _3}^3\frac {{u_1}^7{u_2}^2}{2!\,7!}\\[3pt] &-2{\mu _2}^3\frac {{u_1}^3{u_2}^4}{4!\,3!} +432\mu _6\frac {{u_1}^{11}}{11!} +510{\mu _2}^3\frac {{u_1}^{11}}{11!}\\[3pt] &-\mu _2\mu _5{u_1}^5\frac {u_5u_2}{5!} -\mu _2\mu _5\frac {u_5{u_2}^3u_1}{3} +288\mu _2\mu _5\frac {{u_1}^{10}u_2}{10!}+\cdots . \end{align*}