Published online by Cambridge University Press: 18 December 2014
(0.1)in the whole Hyperbolic space ℍN. We establish decay estimates and symmetry properties of positive solutions. Unlike the corresponding problem in Euclidean space ℝN, we prove that there is a positive solution pair (u, v) ∈ H1(ℍN) × H1(ℍN) of problem (0.1), moreover a ground state solution is obtained. Furthermore, we also prove that the above problem has a radial positive solution.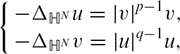 \begin{equation}\label{eq:0.1}\left\{\begin{array}{ll}\displaystyle-\Delta_{\mathbb{H}^{N}}u=|v|^{p-1}v x, \\\displaystyle-\Delta_{\mathbb{H}^{N}}v=|u|^{q-1}u, \\\end{array}\right.\end{equation}
\begin{equation}\label{eq:0.1}\left\{\begin{array}{ll}\displaystyle-\Delta_{\mathbb{H}^{N}}u=|v|^{p-1}v x, \\\displaystyle-\Delta_{\mathbb{H}^{N}}v=|u|^{q-1}u, \\\end{array}\right.\end{equation}