Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-12T22:22:18.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Symbols for trace class Hankel operators with good estimates for norms

Published online by Cambridge University Press:  18 May 2009

F. F. Bonsall  and
D. Walsh
F. F. Bonsall
Affiliation:
Departmant of Mathematics, University of Edinburgh
D. Walsh
Affiliation:
Department of Mathematics, Maynooth College, Co. Kildare
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

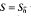Peller [4, 5] has proved that a Hankel operator S on the Hardy space H2 is in the trace class if and only if with h analytic on the open unit disc Dand with its second derivative belonging to the Bergman space L1a. This theorem does not include an estimate for the trace class norm ∥S∥1, of the operator in terms of the symbol function. In fact it is clear that 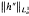cannot give an estimate for 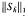since the first two terms in the coefficient sequence of the Hankel operator have been removed by differentiation.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 28 , Issue 1 , January 1986 , pp. 47 - 54
Copyright
Copyright © Glasgow Mathematical Journal Trust 1986

References

REFERENCES

1.Anderson, J. M., Clunie, J. and Pommerenke, Ch., On Bloch functions and normal functions, J. Reine Angew. Math. 270 (1974), 12–37.Google Scholar
2.Bonsall, F. F., Decompositions of functions as sums of elementary function, Quart. J. Math. (Oxford), to appear.Google Scholar
3.Coifman, R. R. and Rochberg, R., Representation theorems for holomorphic and harmonic functions in Lp, Asterisque 77 (1980), 11–66.Google Scholar
4.Peller, V. V., Hankel operators of class and their applications (Rational approximation, Gaussian processes, the problem ofmajorizing operators), Mat. Sbornik 113 (1980) No. 4, 538–581 (Russian). English translation: Math. USSR Sbornik41 (1982), No. 4, 443–479.Google Scholar
5.Peller, V. V., Nuclearity of Hankel operators Preprint, Leningrad (1979).Google Scholar
6.Peller, V. V., Continuity of the averaging projection onto the set of Hankel matrices II, Preprint, Leningrad (1983).Google Scholar
7.Peller, V. V., Continuity of the averaging projection onto the set of Hankel matrices II, Preprint, Leningrad (1983).Google Scholar
8.Power, S. C., Hankel operators on Hilbert space, Research notes in mathematics 64 (Pitman, 1982).Google Scholar