No CrossRef data available.
Article contents
Sur une question de localisation
Published online by Cambridge University Press: 18 May 2009
Extract
II est connu [4] que si A = U(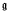 ) est l'algèbre enveloppante d'une algèbre de Lie nilpotente
) est l'algèbre enveloppante d'une algèbre de Lie nilpotente 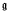 de dimension finie sur un corps F de caractéristique 0, tout idéal (complètement) premier P a pourlocalisé R = Ap un anneau régulier au sens de [5]; c'est-à-dire que le radical de Jacobson
de dimension finie sur un corps F de caractéristique 0, tout idéal (complètement) premier P a pourlocalisé R = Ap un anneau régulier au sens de [5]; c'est-à-dire que le radical de Jacobson 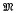 de R est engendrè par une suite centralisante régulière de longueur n = K-dim R, soit (z1…, zn). Dans le cas très particulier où P est l'idéal d'augmentation de U(
de R est engendrè par une suite centralisante régulière de longueur n = K-dim R, soit (z1…, zn). Dans le cas très particulier où P est l'idéal d'augmentation de U(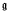 ) il suffit de prendre pour (z1…, zn) l'image dans U(
) il suffit de prendre pour (z1…, zn) l'image dans U(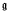 )p d'une base de
)p d'une base de 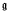 sur F adaptée à la suite centrale ascendante de
sur F adaptée à la suite centrale ascendante de 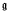 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1981


