Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T19:15:58.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Support projections on Banach spaces

Published online by Cambridge University Press:  18 May 2009

P. G. Spain
P. G. Spain
Affiliation:
Department of Mathematics, University of Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Each bounded linear operator a on a Hilbert space K has a hermitian left-support projection p such that 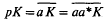and (1 – p)K = ker α* = ker αα*. I demonstrate here that certain operators on Banach spaces also have left supports.

Throughout this paper X will be a complex Banach space with norm-dual X', and L(X) will be the Banach algebra of bounded linear operators on X. Two linear subspaces Y and Z of X are orthogonal (in the sense of G. Birkhoff) if ∥ y ∥ ≦ ∥ y + z ∥ (y ∈Y, z ∈ Z); this orthogonality relation is not, in general, symmetric. It is easy to see that pX is orthogonal to (1 – p)X if and only if the norm of p is 0 or 1, when p is a projection on X.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 18 , Issue 1 , January 1977 , pp. 13 - 15
Copyright
Copyright © Glasgow Mathematical Journal Trust 1977

References

1.Barnes, B. A., Representations of B*-algebras on Banach spaces, Pacific J. Math. 50 (1974), 7–18.CrossRefGoogle Scholar
2.Bonsall, F. F. and Duncan, J., Numerical ranges of operators on normed spaces and of elements of normed algebras (Cambridge U.P., 1971).CrossRefGoogle Scholar
3.Bonsall, F. F. and Duncan, J., Numerical ranges II (Cambridge U.P., 1973).CrossRefGoogle Scholar
4.Dunford, N. and Schwartz, J. T., Linear operators (Interscience, 1958, 1963, 1971).Google Scholar
5.Sakai, S., C*-algebras and W*-algebras (Springer-Verlag, 1971).Google Scholar
6.Sinclair, A. M., Eigenvalues in the boundary of the numerical range, Pacific J. Math. 35 (1970), 231–234.CrossRefGoogle Scholar
7.Spain, P. G., On commutative K*-algebras II, Glasgow Math. J. 13 (1972), 129–134.CrossRefGoogle Scholar
8.Spain, P. G., The W*-closure of a V*-algebra, J. London Math. Soc. (2) 7 (1973), 385–386.Google Scholar