Article contents
Substitutional lemma for G-spaces of 1-dimensional groups
Published online by Cambridge University Press: 18 May 2009
Extract
Let G be a compact Lie group and X a G-CW complex. We are interested in the calculation of the Borel cohomology of X
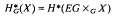
where EG is a universal free G-space and we use on the right hand side cellular cohomology. For an introduction to G-CW complexes see Matumoto [4] and for a good exposition on Borel cohomology see for instance torn Dieck [2], We want to replace X with an ordinary CW complex Y in order to find an ordinary CW structure on the Borel construction EG ΧGY so we can use cellular chains to compute the Borel cohomology of X. For every compact Lie group one has an extension
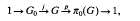
where G0 is the identity component, so for our case G0 is isomorphic to the circle group 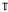 . We are dealing with the case in which π0(G) is isomorphic to C2, the cyclic group of order
. We are dealing with the case in which π0(G) is isomorphic to C2, the cyclic group of order
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1996
References
REFERENCES
- 1
- Cited by


