Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T09:22:08.076Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBMODULES OF COMMUTATIVE C*-ALGEBRAS

Published online by Cambridge University Press:  13 August 2013

NAZAR MIHEISI
NAZAR MIHEISI*
Affiliation:
Department of Pure Mathematics, University of Leeds, Leeds LS2 9JT, United Kingdom e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we generalise a result of Izuchi and Suárez (K. Izuchi and D. Suárez, Norm-closed invariant subspaces in L∞ and H∞, Glasgow Math. J. 46 (2004), 399–404) on the shift invariant subspaces of 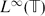$L^\infty(\mathbb{T})$ to the non-commutative setting. Considering these subspaces as 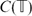$C(\mathbb{T})$-modules contained in 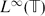$L^\infty(\mathbb{T})$, we show that under some restrictions, a similar description can be given for the 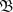${\mathfrak{B}}$-submodules of 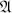${\mathfrak{A}}$, where 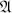${\mathfrak{A}}$ is a C*-algebra and 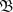${\mathfrak{B}}$ is a commutative C*-subalgebra of 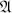${\mathfrak{A}}$. We use this to give a description of the 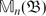$\mathbb{M}_n({\mathfrak{B}})$-submodules of 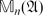$\mathbb{M}_n({\mathfrak{A}})$.

Keywords

46L9947A1547L30
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 56 , Issue 2 , May 2014 , pp. 471 - 479
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Dixmier, J., C*-algebras (North-Holland, New York, NY, 1969).Google Scholar
2.Gamelin, T. W., Uniform algebras (Prentice-Hall, Upper Saddle River, NJ, 1969).Google Scholar
3.Garnett, J. B., Bounded analytic functions (Academic Press, London, 1981).Google Scholar
4.Glicksberg, I., Measures orthogonal to algebras and sets of antisymmetry, Trans. Amer. Math. Soc. 105 (3) (1962), 415–435.CrossRefGoogle Scholar
5.Izuchi, K. and Suárez, D., Norm closed invariant subspaces in L ∞ and H ∞, Glasgow Math. J. 46 (2004), 399–404.Google Scholar
6.Kadison, R. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras, vol. 2 (Academic Press, London, 1986).Google Scholar
7.Partington, J. R., Linear operators and linear systems: an analytical approach to control theory (Cambridge University Press, Cambridge, UK, 2004).Google Scholar
8.Szymanski, W., Antisymmetric operator algebras 1, Ann. Polon. Math. 37 (1980), 263–274.CrossRefGoogle Scholar
9.Szymanski, W., Antisymmetric operator algebras 2, Ann. Polon. Math. 37 (1980), 299–311.Google Scholar