Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T23:04:34.581Z Has data issue: false hasContentIssue false
  • English
  • Français

Subgroups of infinite index in the modular group II

Published online by Cambridge University Press:  18 May 2009

W. W. Stothers
W. W. Stothers
Affiliation:
University of Glasgow, Glasgow, G12 8QW
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H be a subgroup of Γ, the modular group. Let h be the number of orbits of 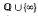under the action of H. In each orbit, the stabilizers are H-conjugate. Let U be the mapping z↦z + 1. Each stabilizer is Γ-conjugate to 〈Uc〉 for some non-negative integer c. The integer c is the cusp-width of the orbit. Let h0 be the number of orbits with non-trivial stabilizer, i.e. with c>0. The sequence (c(1), …, c(h0)) of non-zero cuspwidths is the cusp-split of H. Clearly, h0<h, and h∞ = h−h0 is the number of orbits with trivial stabilizer.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 22 , Issue 1 , January 1981 , pp. 101 - 118
Copyright
Copyright © Glasgow Mathematical Journal Trust 1981

References

REFERENCES

1.Jones, G. A. and Singerman, D., Theory of maps on orientable surfaces, Proc. London Math. Soc. (3) 37 (1978), 273–307.CrossRefGoogle Scholar
2.Jones, G. A., Triangular maps and non-congruence subgroups of the modular group, Bull. London Math. Soc. 11 (1979), 117–123.CrossRefGoogle Scholar
3.Millington, M. H., Subgroups of the classical modular group, J. London Math. Soc. (2) 1 (1969), 351–357.CrossRefGoogle Scholar
4.Stothers, W. W., Subgroups of infinite index in the modular group, Glasgow Math. J. 19 (1978), 33–43.CrossRefGoogle Scholar
5.Stothers, W. W., The number of subgroups of given index in the modular group, Proc. Roy. Soc. Edinburgh Sect. A 78 (1977), 105–112.CrossRefGoogle Scholar
6.Stothers, W. W., Diagrams associated with subgroups of Fuchsian groups, Glasgow Math. J. 20 (1979), 103–114.CrossRefGoogle Scholar