No CrossRef data available.
Article contents
Strong bands of groups of left quotients
Published online by Cambridge University Press: 18 May 2009
Extract
An interesting concept of semigroups (and also rings) of (left) quotients, based on the notion of group inverse in a semigroup, was developed by J. B. Fountain, V. Gould and M. Petrich, in a series of papers (see [5]-[12]). Among the most interesting are semigroups having a semigroup of (left) quotients that is a union of groups. Such semigroups have been widely studied. Recall from [3] that a semigroup has a group of left quotients if and only if it is right reversible and cancellative. A more general result was obtained by V. Gould [10]. She proved that a semigroup has a semilattice of groups as its semigroup of left quotients if and only if it is a semilattice of right reversible, cancellative semigroups. This result has been since generalized by A. El-Qallali [4]. He proved that a semigroup has a left regular band of groups as its semigroup of left quotients if and only if it is a left regular band of right reversible, cancellative semigroups. Moreover, he proved that such semigroups can be also characterised as punched spined products of a left regular band and a semilattice of right reversible, cancellative semigroups. If we consider the proofs of their theorems, we will observe that the principal problem treated there can be formulated in the following way: Given a semigroup S that is a band B of right reversible, cancellative semigroups Si, i ε B, to each Si, we can associate its group of left quotients Gi. When is it possible to define a multiplication of 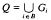 such that Q becomes a semigroup having S as its left order, and especially, that Q becomes a band B of groups Gi, i E B?Applying the methods developed in [1] (see also [2]), in the present paper we show how this problem can be solved for Qto become a strong band of groups (that is in fact a band of groups whose idempotents form a subsemigroup, by [16, Theorem 2]. Moreover, we show how Gould's and El-Quallali's constructions of semigroups of left quotients of a semilattice and a left regular band of right reversible, cancellative semigroups, can be simplified.
such that Q becomes a semigroup having S as its left order, and especially, that Q becomes a band B of groups Gi, i E B?Applying the methods developed in [1] (see also [2]), in the present paper we show how this problem can be solved for Qto become a strong band of groups (that is in fact a band of groups whose idempotents form a subsemigroup, by [16, Theorem 2]. Moreover, we show how Gould's and El-Quallali's constructions of semigroups of left quotients of a semilattice and a left regular band of right reversible, cancellative semigroups, can be simplified.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1996


