Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T17:43:22.470Z Has data issue: false hasContentIssue false
  • English
  • Français

STABLE PROPERTIES OF HYPERRELEXIVITY

Part of: Modules, bimodules and ideals Linear spaces and algebras of operators

Published online by Cambridge University Press:  21 July 2015

G. K. ELEFTHERAKIS
G. K. ELEFTHERAKIS*
Affiliation:
Department of Mathematics, Faculty of Sciences, University of Patras, 26500 Patras, Greece e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, a new equivalence relation between weak* closed operator spaces acting on Hilbert spaces has appeared. Two weak* closed operator spaces 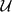${\mathcal{U}}$, 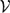${\mathcal{V}}$ are called weak TRO equivalent if there exist ternary rings of operators 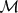${\mathcal{M}}$i, i = 1, 2 such that 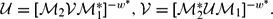${\mathcal{U}}=[{\mathcal{M}}_2{\mathcal{V}}{\mathcal{M}}_1^*]^{-w^*}, {\mathcal{V}}=[{\mathcal{M}}_2^*{\mathcal{U}}{\mathcal{M}}_1]^{-w^*}.$ Weak TRO equivalent spaces are stably isomorphic, and conversely, stably isomorphic dual operator spaces have normal completely isometric representations with weak TRO equivalent images. In this paper, we prove that if 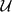${\mathcal{U}}$ and 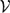${\mathcal{V}}$ are weak TRO equivalent operator spaces and the space of I × I matrices with entries in 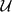${\mathcal{U}}$, MIw(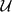${\mathcal{U}}$), is hyperreflexive for suitable infinite I, then so is MIw(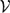${\mathcal{V}}$). We describe situations where if 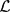${\mathcal{L}}$1, 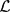${\mathcal{L}}$2 are isomorphic lattices, then the corresponding algebras Alg(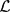$\mathcal{L}$1), Alg(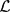$\mathcal{L}$2) have the same complete hyperreflexivity constant.

MSC classification

Primary: 47L05: Linear spaces of operators
Secondary: 47L35: Nest algebras, CSL algebras 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 58 , Issue 1 , January 2016 , pp. 205 - 218
Copyright
Copyright © Glasgow Mathematical Journal Trust 2015 

References

REFERENCES

1.Blecher, D. P. and Le Merdy, C., Operator algebras and their modules – an operator space approach (Oxford University Press, UK, 2004).CrossRefGoogle Scholar
2.Davidson, K. R. and Levene, R. H., 1-hyperreflexivity and complete hyperreflexivity, J. Funct. Anal. 235 (2) (2006), 666–701.CrossRefGoogle Scholar
3.Eleftherakis, G. K., TRO equivalent algebras, Houston J. Math. 38 (1) (2012), 153–175.Google Scholar
4.Eleftherakis, G. K., Morita type equivalences and reflexive algebras, J. Operator Theory 64 (1) (2010), 3–17.Google Scholar
5.Eleftherakis, G. K., Stable isomorphism and strong Morita equivalence of operator algebras, Houston J. Math. (to appear).Google Scholar
6.Eleftherakis, G. K. and Paulsen, V. I., Stably isomorphic dual operator algebras, Math. Ann. 341 (1) (2008), 99–112.CrossRefGoogle Scholar
7.Eleftherakis, G. K., Paulsen, V. I. and Todorov, I. G., Stable isomorphism of dual operator spaces, J. Funct. Anal. 258 (2010), 260–278.CrossRefGoogle Scholar
8.Erdos, J. A., Reflexivity for subspace maps and linear spaces of operators, Proc. London Math. Soc. 52 (3) (1986), 582–600.CrossRefGoogle Scholar
9.Katavolos, A. and Todorov, I. G., Normalisers of operator algebras and reflexivity, Proc. London Math. Soc. 86 (3) (2003), 463–484.CrossRefGoogle Scholar
10.Kraus, J. and Larson, D., Reflexivity and distance formulae, Proc. London Math. Soc. 53 (1986), 340–356.CrossRefGoogle Scholar