Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T09:30:20.043Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME RESULTS OF THE 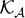$\mathcal K_{\mathcal A}$-APPROXIMATION PROPERTY FOR BANACH SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices Linear spaces and algebras of operators

Published online by Cambridge University Press:  09 August 2018

JU MYUNG KIM
JU MYUNG KIM*
Affiliation:
Department of Mathematics, Sejong University, Seoul 05006, South Korea e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a Banach operator ideal 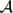$\mathcal A$, we investigate the approximation property related to the ideal of 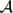$\mathcal A$-compact operators, 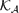$\mathcal K_{\mathcal A}$-AP. We prove that a Banach space X has the 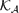$\mathcal K_{\mathcal A}$-AP if and only if there exists a λ ≥ 1 such that for every Banach space Y and every R ∈ 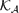$\mathcal K_{\mathcal A}$(Y, X),

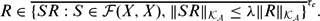$$ \begin{equation} R \in \overline {\{SR : S \in \mathcal F(X, X), \|SR\|_{\mathcal K_{\mathcal A}} \leq \lambda \|R\|_{\mathcal K_{\mathcal A}}\}}^{\tau_{c}}. \end{equation} $$
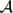For a surjective, maximal and right-accessible Banach operator ideal $\mathcal A$, we prove that a Banach space X has the 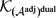$\mathcal K_{(\mathcal A^{{\rm adj}})^{{\rm dual}}}$-AP if the dual space of X has the 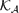$\mathcal K_{\mathcal A}$-AP.

MSC classification

Primary: 46B28: Spaces of operators; tensor products; approximation properties
Secondary: 46B45: Banach sequence spaces 47L20: Operator ideals
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 61 , Issue 3 , September 2019 , pp. 545 - 555
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

References

REFERENCES

Carl, B. and Stephani, I., On A-compact operators, generalized entropy numbers and entropy ideals, Math. Nachr. 199 (1984), 77–95.CrossRefGoogle Scholar
Choi, Y. S. and Kim, J. M., The dual space of ($\mathcal L$(X, Y), τp) and the p-approximation property, J. Funct. Anal. 259 (2010), 2437–2454.CrossRefGoogle Scholar
Defant, A. and Floret, K., Tensor norms and operator ideals (Elsevier, North-Holland, 1993).Google Scholar
Delgado, J. M. and Piñeiro, C., An approximation property with respect to an operator ideal, Stud. Math. 214 (2013), 67–75.CrossRefGoogle Scholar
Delgado, J. M., Piñeiro, C. and Serrano, E., Density of finite rank operators in the Banach space of p-compact operators, J. Math. Anal. Appl. 370 (2010), 498–505.CrossRefGoogle Scholar
Delgado, J. M., Piñeiro, C. and Serrano, E., Operators whose adjoints are quasi p-nuclear, Stud. Math. 197 (2010), 291–304.CrossRefGoogle Scholar
Delgado, J. M., Oja, E., Piñeiro, C. and Serrano, E., The p-approximation property in terms of density of finite rank operators, J. Math. Anal. Appl. 354 (2009), 159–164.CrossRefGoogle Scholar
Fourie, J. H. and Swart, J., Banach ideals of p-compact operators, Manuscripta Math. 26 (1979), 349–362.CrossRefGoogle Scholar
Fourie, J. H. and Swart, J., Tensor products and Banach ideals of p-compact operators, Manuscripta Math. 35 (1981), 343–351.CrossRefGoogle Scholar
Galicer, D., Lassalle, S., and Turco, P., The ideal of p-compact operators: a tensor product approach, Stud. Math. 211 (2012), 269–286.CrossRefGoogle Scholar
Grothendieck, A., Produits tensoriels topologiques et espaces nucléaires, Mem. Amer. Math. Soc. 16 (1955).Google Scholar
Kim, J. M., The $\mathcal K_{up}$-approximation property and its duality, J. Aust. Math. Soc. 98 (2015), 364–374.CrossRefGoogle Scholar
Kim, J. M., Unconditionally p-null sequences and unconditionally p-compact operators, Stud. Math. 224 (2014), 133–142.CrossRefGoogle Scholar
Kim, J. M., The ideal of unconditionally p-compact operators, Rocky Mt. J. Math. 47 (2017), 2277–2293.CrossRefGoogle Scholar
Kim, J. M., Duality between the $\mathcal K_{1}$- and the $\mathcal K_{u1}$-approximation properties, Houst. J. Math. 43 (2017), 1133–1145.Google Scholar
Lassalle, S. and Turco, P., On p-compact mappings and the p-approximation properties, J. Math. Anal. Appl. 389 (2012), 1204–1221.CrossRefGoogle Scholar
Lassalle, S. and Turco, P., The Banach ideal of $\mathcal A$-compact operators and related approximation properties, J. Funct. Anal. 265 (2013), 2452–2464.CrossRefGoogle Scholar
Lassalle, S. and Turco, P., On null sequences for Banach operator ideals, trace duality and approximation properties, Math. Nachr. 290 (2017), 2308–2321.CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces I, sequence spaces (Springer, Berlin, 1977).Google Scholar
Megginson, R. E., An introduction to Banach space theory (Springer, New York, 1998).CrossRefGoogle Scholar
Oja, E., A remark on the approximation of p-compact operators by finite-rank operators, J. Math. Anal. Appl. 387 (2012), 949–952.CrossRefGoogle Scholar
Pietsch, A., Operator ideals (North-Holland, Amsterdam, 1980).Google Scholar
Ryan, R. A., Introduction to tensor products of Banach spaces (Springer, Berlin, 2002).CrossRefGoogle Scholar
Sinha, D. P. and Karn, A. K., Compact operators whose adjoints factor through subspaces of ℓp, Stud. Math. 150 (2002), 17–33.CrossRefGoogle Scholar
Sinha, D. P. and Karn, A. K., Compact operators which factor through subspaces of ℓp, Math. Nachr. 281 (2008), 412–423.CrossRefGoogle Scholar