Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-03T20:29:08.926Z Has data issue: false hasContentIssue false
  • English
  • Français

The solution of certain simultaneous pairs of dual integral equations†

Published online by Cambridge University Press:  18 May 2009

M. Lowengrub
M. Lowengrub
Affiliation:
Duke UniversityUniversity of Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the analysis of mixed boundary value problems by Hankel transforms, one often encounters dual integral equations of the form

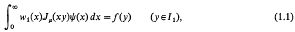
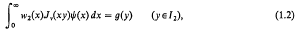
where I1 = (0, 1), I2 = (1, ∞); w1(x), w2(x) are weight functions, ψ(x) is the unknown function, and f(y), g(y) are functions continuously differentiate on I1 and I2 respectively. Many successful attempts have been made to solve (1.1) and (1.2). These are all discussed in a recent book by Sneddon [7]. As pointed out in a recent paper by Erdogan and Bahar [4], in mixed boundary value problems of semi-infinite domains involving more than one unknown function such as those arising in elastostatics, viscoelasticity, and electrostatics, the formulation will lead to a system of simultaneous dual integral equations which is a generalization of (1.1) and (1.2). These equations may be expressed as follows:

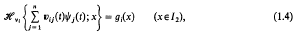
with i = 1, 2, …, n, where we use the notation

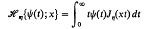
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 9 , Issue 2 , July 1968 , pp. 92 - 102
Copyright
Copyright © Glasgow Mathematical Journal Trust 1968

References

REFERENCES

1.Abramowitz, M. and Stetgun, I. A., Handbook of mathematical functions (Nat. Bureau of Standards, App. Math. Series 55, 1964).Google Scholar
2.Copson, E. T., On certain dual integral equations, Proc. Glasgow Math. Assoc. 5 (1961), 21–24.CrossRefGoogle Scholar
3.Erdelyi, A. and Sneddon, I. N., Fractional integration and dual integral equations, Canad. J. Math. 14 (1962), 685–693.CrossRefGoogle Scholar
4.Erdogan, F. and Bahar, L. Y., On the solution of simultaneous dual integral equations, S.I.A.M. Journal 12 (1964), 666–675.Google Scholar
5.Lowengrub, M. and Sneddon, I. N., The solution of a pair of dual integral equations, Proc. Glasgow Math. Assoc. 6 (1963), 14–18.CrossRefGoogle Scholar
6.Peters, A. S., Certain dual integral equations and Sonine's integral (Technical report Imm-NYU 285, Inst. Math. Sci. NYU 08, 1961).Google Scholar
7.Sneddon, I. N., Mixed boundary value problems of potential theory (North Holland Publishing Co. Amsterdam, 1966).Google Scholar
8.Sneddon, I. N. and Lowengrub, M., Crack problems in the classical theory of elasticity (New York, 1968).Google Scholar
9.Tranter, C. J., Integral Transforms in Mathematical Physics (New York, 1956).Google Scholar
10.Westmann, R. A., Simultaneous pairs of dual integral equations, SIAM Rev. 7 (1965), 341–348.CrossRefGoogle Scholar