Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-30T16:11:21.659Z Has data issue: false hasContentIssue false
  • English
  • Français

A Simple proof of the Goldberg–Straus theorem on numerical radii

Published online by Cambridge University Press:  18 May 2009

Bit-Shun Tam
Bit-Shun Tam
Affiliation:
Department of Mathematics, Tamkang University, Taipei, Taiwan 251, Republic of China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

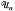Let Mn(ℂ) be the algebra of n × n complex matrices, and let be its unitary group. Given A, B ε Mn(ℂ), the A-numerical radius of B is the nonnegative quantity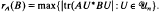

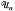In particular, for A = diag(1, 0, …, 0) it reduces to the classical numerical radius r(B) = max||x*Bx|:x*x = 1}. In [1] Goldberg and Straus proved that rA is a generalized matrix norm (i.e. a positive definite seminorm) on Mn(ℂ) if and only if A is nonscalar and tr A ≠ 0. This result agrees with the well-known fact that the classical numerical radius r is a generalized matrix norm. The nontrivial part of the proof is to show that if A is nonscalar and tr A ≠ 0 then rA is positive definite; that is, for any B ε Mn(ℂ), tr(AU*BU) = 0 for all U ε implies B = 0. The proof given in [1] is computational and involves the use of differentiation on matrices. Later Marcus and Sandy [2] gave three elementary proofs of the result. Their proofs are still computational in nature and two of them need knowledge of multilinear algebra.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 28 , Issue 2 , July 1986 , pp. 139 - 141
Copyright
Copyright © Glasgow Mathematical Journal Trust 1986

References

REFERENCES

1.Goldberg, M. and Straus, E. G., Norm properties of C-numerical radii, Linear Algebra and Appl. 24 (1979), 113–131.CrossRefGoogle Scholar
2.Marcus, M. and Sandy, M., Three elementary proofs of the Goldberg–Straus theorem on numerical radii, Linear and Multilinear Algebra 11 (1982), 243–252.CrossRefGoogle Scholar
3.Tam, B. S., The action of unitary transforms of a matrix on linear subspaces, submitted for publication.Google Scholar
4.Tam, T. Y., On the generalized radial matrices and a conjecture of Marcus and Sandy, Linear and Multilinear Algebra, to appear.Google Scholar