A simple proof of Noether's theorem

Extract

We present an elementary proof of the theorem, usually attributed to Noether, that if L/K is a tame finite Galois extension of local fields, then 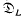is a free 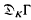-module where Γ=Gal(L/K. The attribution to Noether is slightly misleading as she only states and proves the result in the case where the residual characteristic of K does not divide the order of Γ [4]. In this case 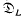is a maximal order in KΓ which is not true for general groups Γ. There is an elegant proof in the standard reference [2], but this relies on a difficult result in representation theory due to Swan. Our proof depends on a close examination of the structure of tame local extensions, and uses only elementary facts about local fields. It also gives an explicit construction of a generator element, and the same proof works both for localizations of number fields and of global function fields.