Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T20:41:41.206Z Has data issue: false hasContentIssue false
  • English
  • Français

SCALAR CURVATURE OF HYPERSURFACES WITH CONSTANT MEAN CURVATURE IN A SPHERE

Published online by Cambridge University Press:  01 May 2009

QING-MING CHENG ,
YIJUN HE  and
HAIZHONG LI
QING-MING CHENG
Affiliation:
Department of Mathematics, Faculty of Sciences and Engineering, Saga University, Saga 840-8502, Japan e-mail: [email protected]
YIJUN HE*
Affiliation:
School of Mathematical Sciences, Shanxi University, Taiyuan 030006, P.R. China e-mail: [email protected]
HAIZHONG LI
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, P.R. China e-mail: [email protected]
*
†Corresponding author, partially supported by Youth Science Foundation of Shanxi Province, China (2006021001).
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be an n-dimensional closed hypersurface with constant mean curvature H satisfying |H| ≤ ϵ(n) in a unit sphere Sn+1, n ≤ 7, and S the square of the length of the second fundamental form of M. There exists a constant δ(n, H) > 0, which depends only on n and H, such that if S0 ≤ S ≤ S0 + δ(n, H), then S ≡ S0 and M is isometric to a Clifford hypersurface, where ϵ(n) is a sufficiently small constant depending on n and .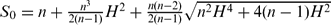

Keywords

Primary 53C42Secondary 53B25
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 2 , May 2009 , pp. 413 - 423
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Chen, B. Y., Mean curvature and shape operator of isometric immersions in real-space-forms, Glasgow Math. J. 38 (1996), 87–97.CrossRefGoogle Scholar
2.Cheng, Q. M. and Ishikawa, S., A characterization of the Clifford torus, Proc. Am. Math. Soc. 127 (1999), 819–828.CrossRefGoogle Scholar
3.Cheng, Q. M. and Yang, H. C., Chern's conjecture on minimal hypersurfaces, Math. Z. 227 (1998), 377–390.Google Scholar
4.Chern, S. S., do Carmo, M. and Kobayashi, S., Minimal submanifolds of constant length, in Functional analysis and related fields (Browder, F. E., ed.) (Springer, New York 1970), 59–75.Google Scholar
5.Lawson, B., Local rigidity theorems for minimal hypersurfaces, Ann. Math. 89 (1969), 187–197.CrossRefGoogle Scholar
6.Li, H., Hypersurfaces with constant scalar curvature in space forms, Math. Ann. 305 (1996), 665–672.Google Scholar
7.Li, H., Scalar curvature of hypersurfaces with constant mean curvature in spheres, Tsinghua Sci. Technol. 1 (1996), 266–269.Google Scholar
8.Okumura, M., Hypersurfaces and a pinching problem on the second fundamental tensor, Am. J. Math. 96 (1974), 207–213.CrossRefGoogle Scholar
9.Peng, C. K. and Terng, C. L., Minimal hypersurfaces of sphere with constant scalar curvature, Ann. Math. Stud. 103 (1983), 177–198.Google Scholar
10.Peng, C. K. and Terng, C. L., The scalar curvature of minimal hypersurfaces in spheres, Math. Ann. 266 (1983), 105–113.CrossRefGoogle Scholar
11.Simons, J., Minimal varieties in Riemannian manifolds, Ann. Math. 88 (1968), 62–105.CrossRefGoogle Scholar
12.Wei, S. M. and Xu, H. W., Scalar curvature of minimal hypersurfaces in a sphere, Math. Res. Lett. 14 (2007), 423–432.CrossRefGoogle Scholar
13.Yau, S. T., Problem section, Annals of Math. Studies, No. 102 (Princeton University Press, Princeton, NJ, 1982), 693.Google Scholar