No CrossRef data available.
Article contents
Results on common fixed points on complete metric spaces
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The following theorem was proved in [1].
Theorem 1. Let S and T be continuous, commuting mappings of a complete, bounded metric space (X, d) into itself satisfying the inequality
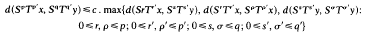
for all x, y in X, where 0 ≤ c < 1 and p, p′, q, q′ ≥ 0 are fixed integers with p + p′, q + q′ ≥ 1. Then S and T have a unique common fixed point z. Further, if p′ or q′ = 0, then z is the unique fixed point of S and if p or q = 0, then z is the unique fixed point of T.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1980
References
REFERENCE
1.Fisher, B., Results on common fixed points on bounded metric spaces, Math. Sem. Notes Kobe Univ., 7 (1979), 73–80.Google Scholar


