Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-04T15:27:58.575Z Has data issue: false hasContentIssue false
  • English
  • Français

A result on hermitian operators

Published online by Cambridge University Press:  18 May 2009

J. E. Jamison  and
Pei-Kee Lin
J. E. Jamison
Affiliation:
Department of Mathematics, Memphis State University, Memphis, Tennessee 38152, U.S.A.
Pei-Kee Lin
Affiliation:
Department of Mathematics, Memphis State University, Memphis, Tennessee 38152, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a complex Banach space. For any bounded linear operator T on X, the (spatial) numerical range of T is denned as the set

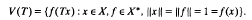
If V(T) ⊆ R, then T is called hermitian. Vidav and Palmer (see Theorem 6 of [3, p. 78] proved that if the set {H + iK:H and K are hermitian} contains all operators, then X is a Hilbert space. It is natural to ask the following question.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 1 , January 1989 , pp. 71 - 72
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Berkson, E., Some types of Banach spaces, hermitian operators, and Bade functionals, Trans. Amer. Math. Soc. 116 (1965), 376–385.CrossRefGoogle Scholar
2.Berkson, E., A characterization of complex Hilbert spaces, Bull. London Math Soc. 2 (1970), 313–315.CrossRefGoogle Scholar
3.Bonsall, F. F. and Duncan, J., Numerical ranges of operators on normed spaces and of elements of normed algebras, London Math. Soc. Lecture Notes series, 2 (C.U.P., 1971).CrossRefGoogle Scholar
4.Bonsall, F. F. and Duncan, J., Numerical ranges II, London Math. Soc. Lecture Notes Series, 10 (C.U.P., 1973).CrossRefGoogle Scholar
5.Kalton, N. J. and Wood, G. V., Orthonormal systems in Banach spaces and their applications, Math. Proc. Camb. Phil. Soc. 76 (1976), 493–510.CrossRefGoogle Scholar
6.Mattila, K., Normal operators and proper boundary points of the spectra of operators on a Banach space, Ann. Acad. Sci. Fenn. Ser, AI, Math. Dissertations 19 (1978).Google Scholar