Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T20:03:51.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Representation of primes by binary quadratic forms of discriminant –256q and –128q

Published online by Cambridge University Press:  18 May 2009

Franz Halter-Koch
Franz Halter-Koch
Affiliation:
Institut Für MathematikKarl-Franzens-UniversitatHeinrichstrasse 36/IVA–8010 Graz, Osterreich.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, P. Kaplan and K. S. Williams [10] considered (as an example) the representation of primes by binary quadratic forms of discriminant –768. These forms fall into 4 genera, each consisting of two classes. In particular, they considered the forms

F=3X2+642 and G = 12X2+12XY+19Y2.

It follows from genus theory (as explained in [10]) that every prime p ≡ 19 mod 24 is represented by exactly one of the forms F and G. Based on numerical data, they conjectured that a prime p ≡ 19 mod 24 is represented by

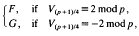
where

Vo = 2, V1 = -4, Vn+2=-4Vn+1 -Vn (n∨0).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 2 , May 1993 , pp. 261 - 268
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Buell, D. A., Binary quadratic forms (Springer-Verlag 1989).CrossRefGoogle Scholar
2.Cohn, H., A classical invitation to algebraic numbers and class fields (Springer-Verlag 1978).CrossRefGoogle Scholar
3.Gurak, S., On the representation theory for full decomposable forms, J. Number Theory 13 (1981), 421–442.CrossRefGoogle Scholar
4.Halter-Koch, F., Quadratische Einheiten als 8. Potenzreste in Proc. Int. Conf. on Class Numbers and Fundamental Units (Katata 1986), 1–15.Google Scholar
5.Halter-Koch, F., Einseinheitengruppen und prime Resklassengruppen in quadratischen Zahlkörpern, J. Number Theory 4 (1972), 70–77.CrossRefGoogle Scholar
6.Halter-Koch, F., Arithmetische Theorie der Normalkörper von 2-Potenzgrad mit Diedergruppe, J. Number Theory 3 (1971), 412–443.CrossRefGoogle Scholar
7.Halter-Koch, F., Geschlechtertheorie der Ringklassenkörper, j. Reine Angew. Math. 250 (1971), 107–108.Google Scholar
8.Halter-Koch, F. and Ishii, N., Ring class fields modulo 8 of and the quartic character of units of for m ≡ 1 mod 8, Osaka J. Math. 26 (1989), 625–646.Google Scholar
9.Halter-Koch, F., Kaplan, P. and Williams, K. S., An Artin character and representations of primes by binary quadratic forms II, Manuscr. Math. 37 (1982), 357–381.CrossRefGoogle Scholar
10.Kaplan, P. and Williams, K. S., Representation of primes in arithmetic progressions by binary quadratic forms, j.Number Theorey, to appear.Google Scholar