Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-05T03:19:38.553Z Has data issue: false hasContentIssue false
  • English
  • Français

REMARKS ON THE DIVISIBILITY OF THE CLASS NUMBERS OF IMAGINARY QUADRATIC FIELDS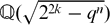

Published online by Cambridge University Press:  21 March 2011

AKIKO ITO
AKIKO ITO*
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya 464-8602, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the divisibility of the class numbers of imaginary quadratic fields 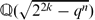, where q is an odd prime number, k and n are positive integers. Suppose that k ≡ 1 mod 2 or n ≢ 3 mod 6. We show that the class numbers of imaginary quadratic fields 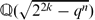≠ 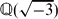are divisible by n for q ≡ 3 mod 8. This is a generalization of the result of Kishi for imaginary quadratic fields 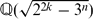when k ≡ 1 mod 2 or n ≢ 3 mod 6. We also show that the class numbers of imaginary quadratic fields 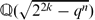≠ 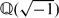are divisible by n for q ≡ 1 mod 4 and the class numbers of imaginary quadratic fields 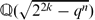≠ 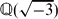are divisible by n for q ≡ 7 mod 8.

Keywords

11R1111R29
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 53 , Issue 2 , May 2011 , pp. 379 - 389
Copyright
Copyright © Glasgow Mathematical Journal Trust 2011

References

REFERENCES

1.Ankeny, N. C. and Chowla, S., On the divisibility of the class number of quadratic fields, Pacific J. Math. 5 (1955), 321–324.CrossRefGoogle Scholar
2.Bugeaud, Y. and Shorey, T. N., On the number of solutions of the generalized Ramanujan–Nagell equation, J. Reine Angew. Math. 539 (2001), 55–74.Google Scholar
3.Cohn, J. H. E., On the class number of certain imaginary quadratic fields, Proc. Amer Math. Soc. 130 (2001), 1275–1277.CrossRefGoogle Scholar
4.Gross, B. H. and Rohrlich, D. E., Some results on the Mordell-Weil group of the Jacobian of the Fermat curve, Invent. Math. 44 (1978), 201–224.CrossRefGoogle Scholar
5.Kishi, Y., Note on the divisibility of the class number of certain imaginary quadratic fields, Glasgow Math. J. 51 (2009), 187–191.CrossRefGoogle Scholar
6.Kishi, Y., Note on the divisibility of the class number of certain imaginary quadratic fields—Corrigendum, Glasgow Math. J. 52 (2010), 207–208.CrossRefGoogle Scholar
7.Nagell, T., Über die Klassenzahl imaginär-quadratischer Zahlkörper, Abh. Math. Sem. Univ. Hamburg 1 (1922), 140–150.CrossRefGoogle Scholar