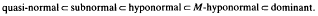Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-04T18:51:20.174Z Has data issue: false hasContentIssue false
  • English
  • Français

A remark on the essential spectra of quasi-similar dominant contractions

Published online by Cambridge University Press:  18 May 2009

B. P. Duggal
B. P. Duggal
Affiliation:
School of Mathematical Sciences, University of Khartoum, P.O. Box 321, Khartoum, Sudan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider operators, i.e. bounded linear transformations, on an infinite dimensional separable complex Hilbert space H into itself. The operator A is said to be dominant if for each complex number λ there exists a number Mλ(≥l) such that ∥(A – λ)*x∥ ≤ Mλ∥A – λ)x∥ for each x∈H. If there exists a number M≥Mλ for all λ, then the dominant operator A is said to be M-hyponormal. The class of dominant (and JW-hyponormal) operators was introduced by J. G. Stampfli during the seventies, and has since been considered in a number of papers, amongst then [7], [11]. It is clear that a 1-hyponormal is hyponormal. The operator A*A is said to be quasi-normal if Acommutes with A*A, and we say that A is subnormal if A has a normal extension. It is known that the classes consisting of these operators satisfy the following strict inclusion relation:

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 2 , May 1989 , pp. 165 - 168
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Clary, S., Equality of spectra of quasi-similar hyponormal operators, Proc. Amer. Math. Soc. 53 (1975), 88–90.CrossRefGoogle Scholar
2.Conway, J. B, Subnormal operators (Pitman, 1981).Google Scholar
3.Douglas, R. G., On the operator equation S*XT = X and related topics, Ada Sci. Math. (Szeged) 30 (1969), 19–32.Google Scholar
4.Duggal, B. P., Intertwining contractions: operator equation AXB = X and AX = XB, Proc. Int. Conf. on ‘Invariant subspaces and allied topics’, University of Delhi, Dec. 1986 (to appear).Google Scholar
5.Gupta, B. C., Quasi-similarity and k-quasihyponormal operators, Math. Today 3 (1985), 49–54.Google Scholar
6.-Nagy, B. Sz. and Foias, C., Harmonic analysis of operators on Hilbert space, (North-Holland, 1970).Google Scholar
7.Stampfli, J. G. and Wadhwa, B. L., An asymmetric Putnam-Fuglede theorem for dominant operators, Indiana Univ. Math. J. 25 (1976), 359–365.CrossRefGoogle Scholar
8.Stampfli, J. G., Quasi-similarity of operators, Proc. Roy. Irish Acad. Sect. A 81 (1981), 109–119.Google Scholar
9.Williams, L. R., Equality of essential spectra of quasi-similar quasinormal operators, j. Operator Theory 3 (1980), 57–69.Google Scholar
10.Williams, L. R., Equality of essential spectra of certain quasi-similar semi-normal operators, Proc. Amer. Math. Soc. 78 (1980), 203–209.CrossRefGoogle Scholar
11.Williams, L. R., Quasi-similarity and hyponormal operators, J. Operator Theory 5 (1981), 127–139.Google Scholar