Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-03T19:19:55.901Z Has data issue: false hasContentIssue false
  • English
  • Français

RELATIVE HILBERT CO-EFFICIENTS

Part of: Commutative algebra: Homological methods General commutative ring theory

Published online by Cambridge University Press:  01 March 2017

AMIR MAFI ,
TONY J. PUTHENPURAKAL ,
RAKESH B. T. REDDY  and
HERO SAREMI
AMIR MAFI
Affiliation:
Department of Mathematics, University of Kurdistan, P.O. Box: 416, Sanandaj, Iran e-mail: [email protected]
TONY J. PUTHENPURAKAL
Affiliation:
Department of Mathematics, IIT Bombay, Powai, Mumbai 400 076, India e-mails: [email protected], [email protected]
RAKESH B. T. REDDY
Affiliation:
Department of Mathematics, IIT Bombay, Powai, Mumbai 400 076, India e-mails: [email protected], [email protected]
HERO SAREMI
Affiliation:
Department of Mathematics, Sanandaj Branch, Islamic Azad University, Sanandaj, Iran e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (A, 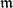${\mathfrak{m}$) be a Cohen–Macaulay local ring of dimension d and let I ⊆ J be two 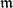${\mathfrak{m}$-primary ideals with I a reduction of J. For i = 0,. . .,d, let eiJ(A) (eiI(A)) be the ith Hilbert coefficient of J (I), respectively. We call the number ci(I, J) = eiJ(A) − eiI(A) the ith relative Hilbert coefficient of J with respect to I. If GI(A) is Cohen–Macaulay, then ci(I, J) satisfy various constraints. We also show that vanishing of some ci(I, J) has strong implications on depth GJn(A) for n ≫ 0.

MSC classification

Primary: 13A30: Associated graded rings of ideals (Rees ring, form ring), analytic spread and related topics
Secondary: 13D40: Hilbert-Samuel and Hilbert-Kunz functions; Poincaré series 13D07: Homological functors on modules (Tor, Ext, etc.)
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 59 , Issue 3 , September 2017 , pp. 729 - 741
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Capani, A., Neisi, G. and Robbiano, L., CoCoA, A system for doing computations in commutative algebra, available via anonymous ftp from cocoa.dima.unige.it 1995.Google Scholar
2. Corso, A., Polini, C. and Vasconcelos, W. V., Links of prime ideals, Math. Proc. Cambridge Phil. Soc. 115 (1994), 431–436.Google Scholar
3. Huckaba, S. and Huneke, C., Normal ideals in regular rings, J. Reine Angew. Math. 510 (1999), 63–82.Google Scholar
4. Huneke, C., Hilbert functions and symbolic powers, Michigan Math. J. 34 (1987), 293–318.Google Scholar
5. Huckaba, S. and Marley, T., Hilbert coefficients and the depths of associated graded rings, J. London Math. Soc. 56 (2) (1997), 64–76.CrossRefGoogle Scholar
6. Itoh, S., Coefficients of normal {H}ilbert polynomials, J. Algebra 150 (1992), 101–117.Google Scholar
7. Jayanthan, A. V. and Ramakrishna, N., On the depth of fiber cones of stretched $\mathfrak{m}$ -primary ideals, Indian J. Pure Appl. Math. 45 (6) (2014), 925–942.CrossRefGoogle Scholar
8. Narita, M., A note on the coefficients of Hilbert characteristic functions in semi-regular local rings, Proc. Camb. Phil. Soc. 59 (1963), 269–275.Google Scholar
9. Marley, T., The coefficients of the Hilbert polynomial and the reduction number of an ideal, J. London Math. Soc. 40 (2) (1989), 1–8.Google Scholar
10. Northcott, D. G., A note on the coefficients of the abstract Hilbert function, J. London Math. Soc. 35 (1960), 209–214.CrossRefGoogle Scholar
11. Ooishi, A., ▵-genera and sectional genera of commutative rings, Hiroshima Math. J. 17 (2) (1987), 361–372.Google Scholar
12. Puthenpurakal, T. J., Ratliff-Rush filtration, regularity and depth of higher associated graded modules Part I, J. Pure Appl. Algebra, 208 (2007), 159–176.Google Scholar
13. Ratliff, L. J. and Rush, D. E., Two notes on reductions of ideals, Indiana Univ. Math. J. 27 (6) (1978), 929–934.CrossRefGoogle Scholar
14. Sally, J., On the associated graded ring of a local Cohen-Macaulay ring, J. Math. Kyoto Univ. 27 (1977), 19–21.Google Scholar