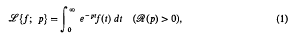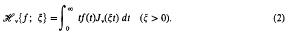Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saxena, R. K.
1963.
A relation between generalized Laplace and Hankel transforms.
Mathematische Zeitschrift,
Vol. 81,
Issue. 5,
p.
414.
Sharma, K. C.
1963.
Theorems relating Hankel and Meijer's Bessel transforms.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 2,
p.
107.
Abdalla, Mohamed
Boulaaras, Salah
and
Akel, Mohamed
2021.
On Fourier–Bessel matrix transforms and applications.
Mathematical Methods in the Applied Sciences,
Vol. 44,
Issue. 14,
p.
11293.
Kumar, Virendra
2021.
On the generalized fractional Laplace transform.
Moroccan Journal of Pure and Applied Analysis,
Vol. 7,
Issue. 3,
p.
448.
KUMAR, Virendra
2023.
Some Relations between Stieltjes Transform and Hankel Transform with Applications.
Communications in Advanced Mathematical Sciences,
Vol. 6,
Issue. 1,
p.
60.