Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-18T14:58:04.309Z Has data issue: false hasContentIssue false
  • English
  • Français

RATIONAL POINTS ON CERTAIN DEL PEZZO SURFACES OF DEGREE ONE

Published online by Cambridge University Press:  01 September 2008

MACIEJ ULAS
MACIEJ ULAS*
Affiliation:
Jagiellonian University, Institute of Mathematics, Reymonta 4, 30-059 Kraków, Poland e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

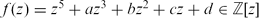Let and let us consider a del Pezzo surface of degree one given by the equation 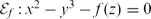. In this paper we prove that if the set of rational points on the curve Ea,b : Y2 = X3 + 135(2a−15)X−1350(5a + 2b − 26) is infinite then the set of rational points on the surface ϵf is dense in the Zariski topology.

Keywords

Primary 11D2511D41Secondary 11G052
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 50 , Issue 3 , September 2008 , pp. 557 - 564
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Bogomolov, F. and Tschinkel, Yu., On the density of rational points on elliptic fibrations, J. Reine und Angew. Math. 511 (1999), 87–93.CrossRefGoogle Scholar
2.Connel, I., APECS: Arithmetic of plane elliptic curves, 2001, available from http://www.math.mcgill.ca/connell/public/apecs/.Google Scholar
3.Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Invent. Math. 73 (1983), 349–366.CrossRefGoogle Scholar
4.Kuwata, M. and Wang, L., Topology of rational points on isotrivial elliptic surfaces, Int. Math. Research Notices 4 (1993), 113–123.CrossRefGoogle Scholar
5.Manduchi, E., Root numbers of fibers of elliptic surfaces, Compos. Math. 99 (1995), 33–58.Google Scholar
6.Manin, Y. I., Cubic forms: Algebra, geometry, arithmetic, 2nd ed. (North-Holland Publishing, Amsterdam, 1986).Google Scholar
7.Munshi, R., Density of positive rank fibers in elliptic fibrations, J. Number Theory 125 (2007) 254–266.CrossRefGoogle Scholar
8.Rohrlich, D. E., Variation of the root number in families of elliptic curves, Compos. Math. 87 (1993), 119–151.Google Scholar
9.Silverman, J., The arithmetic of elliptic curves (Springer-Verlag, New York, 1986).CrossRefGoogle Scholar
10.Ulas, M., Rational points on certain elliptic surfaces, Acta Arith. 129 (2007), 167–185.CrossRefGoogle Scholar