Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-01T03:41:37.763Z Has data issue: false hasContentIssue false
  • English
  • Français

Radicals of semigroup rings†

Published online by Cambridge University Press:  18 May 2009

Julian Weissglass
Julian Weissglass
Affiliation:
University of Wisconsin and University of California, Santa Barbara
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

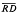Let denote the contracted semigroup ring of the ompletely 0-simple semigroup D over the ring R. The Rees structure theory of completely 0-simple semigroups is used to obtain necessary and sufficient conditions that 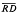have zero radical (Theorem 3.8). By using Amitsur's construction of the upper π-radical [1], we are able to treat the Jacobson, Baer (prime), Levitzki (locally nilpotent) and possibly the nil radicals simultaneously. Our results generalize a theorem of Munn [6] on semigroup algebras of finite 0-simple semigroups.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 10 , Issue 2 , July 1969 , pp. 85 - 93
Copyright
Copyright © Glasgow Mathematical Journal Trust 1969

References

REFERENCES

1.Amitsur, S. A., A general theory of radicals, II, Amer. J. Math. 76 (1954), 100–125.CrossRefGoogle Scholar
2.Amitsur, S. A., A general theory of radicals, III, Amer. J. Math. 76 (1954), 126–136.CrossRefGoogle Scholar
3.Amitsur, S. A., On the semi-simplicity of group algebras, Michigan Math. J. 6 (1959), 251–253.CrossRefGoogle Scholar
4.Clifford, A. H., and Preston, G. B., The algebraic theory of semigroups, Volume 1, Math. Surveys of the American Math. Soc. 7 (Providence, R.I., 1961).Google Scholar
5.Lambek, J., Lectures on rings and modules, (Waltham, Massachusetts 1966).Google Scholar
6.Munn, W. D., On semigroup algebras, Proc. Cambridge Philos. Soc. 51 (1955), 1–15.CrossRefGoogle Scholar
7.Patterson, E. M., On the radicals of certain rings of infinite matrices, Proc. Roy. Soc. Edinburgh Sect. A. 65 (1961), 263–271.Google Scholar
8.Rees, D., On semi-groups, Proc. Cambridge Philos. Soc. 36 (1940), 387–400.CrossRefGoogle Scholar