Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-04T19:26:02.324Z Has data issue: false hasContentIssue false
  • English
  • Français

The quadratic reciprocity law and the elementary theta function

Published online by Cambridge University Press:  18 May 2009

Martin Eichler
Martin Eichler
Affiliation:
27, im Lee CH 4144 Arlesheim, Switzerland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This note points out a new aspect of the well-known relationship between the subjects mentioned in the title. The following result and its generalization in totally real algebraic number fields is central to the discussion. Let 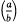denote the Legendre symbol for relatively prime numbers a and b ℇ ℤ and 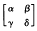a substitution of the modular subgroup Γ0(4). Then, if γ>0 and b≡1 mod 2,

with

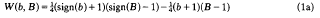
and

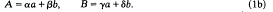
According to (1), the Legendre symbol behaves somewhat like a modular function ﹙apart from the known behaviour under 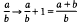and 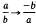﹚. (1) follows (see below) from the functional equation

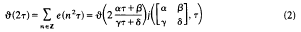
with

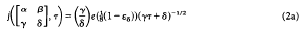
provided that

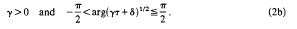
Here we used and always will use the abbreviation

and ℇδ means the absolutely least residue of δ mod 4. In the proof, Hecke [4] assumed γ>0 (see also Shimura [5]).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 27 , October 1985 , pp. 19 - 30
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Eichler, M., Einführung in die Theorie der algebraischen Zahlen und funktionen (Birkhäuser 1963), 55–57, Introduction to Algebraic numbers and functions (Academic Press, 1966), 41–43.CrossRefGoogle Scholar
2.Freitag, E., Siegelsche Modulfunktionen, (Springer, 1982), 2. Anhang, Satz A 2.4.Google Scholar
3.Hecke, E., Mathematische Werke (Vandenhoek und Ruprecht, 1959), No 13.Google Scholar
4.Hecke, E., Mathematische Werke (Vandenhoek und Ruprecht, 1959) No 42, 940.Google Scholar
5.Shimura, G., On modular forms of half integral weight, Ann. Math. 97 (1973), 443.CrossRefGoogle Scholar
6.Siegel, C. L., Gesammelte Abhandlungen, Bd. III. (Springer, 1966).CrossRefGoogle Scholar